- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Задачи по квантовой механике презентация
Содержание
- 1. Задачи по квантовой механике
- 2. Лекция 3. Тепловое излучение. Свободная частица Свободная частица
- 3. Решением данного уравнения является функция:
- 4. Этот факт является исходным
- 5. Лекция 3. Тепловое излучение. Лекция 3.
- 6. Вероятность обнаружить частицу за пределами ямы
- 7. Лекция 3. Тепловое излучение. Лекция 3.
- 8. Решение ищем в виде
- 9. Лекция 3. Тепловое излучение. Лекция 3.
- 10. Получаем собственные волновые функции
- 11. Лекция 3. Тепловое излучение. Лекция 3.
- 13. Уравнение Шредингера имеет вид
- 21. Воспользуемся достигнутыми результатами для того, чтобы рассчитать
- 22. Вероятность обнаружения частицы под потенциальным барьером в
- 23. Эффективная глубина проникновения частицы зависит от ее
Слайд 3
Решением данного уравнения является функция:
(координатная часть плоской волны).
Домножим на
- уравнение плоской волны (волны де Бройля).
Свободная частица
Слайд 4
Этот факт является исходным для квантовой механики. Свободной частице,
Коэффициент С находится из условия нормировки
Свободная частица
Слайд 5Лекция 3. Тепловое излучение.
Лекция 3. Тепловое излучение.
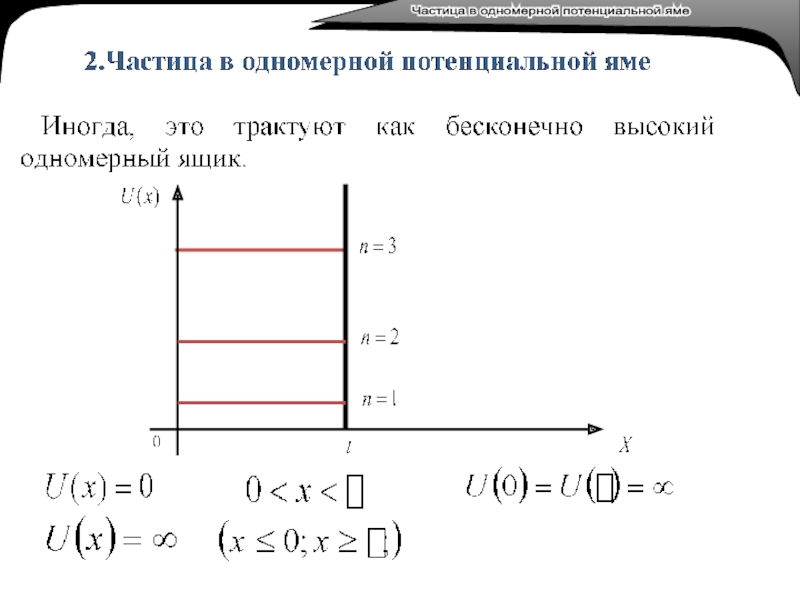
Частица в одномерной
Частица в одномерной потенциальной яме
Слайд 6
Вероятность обнаружить частицу за пределами ямы равна нулю.
Граничные условия:
Частица в
Слайд 7Лекция 3. Тепловое излучение.
Лекция 3. Тепловое излучение.
Частица в одномерной
Частица в одномерной потенциальной яме
Слайд 8
Решение ищем в виде
Используем граничные условия
Волновое число квантуется
Частица в одномерной потенциальной яме
Слайд 9Лекция 3. Тепловое излучение.
Лекция 3. Тепловое излучение.
Частица в одномерной
Частица в одномерной потенциальной яме
Слайд 10
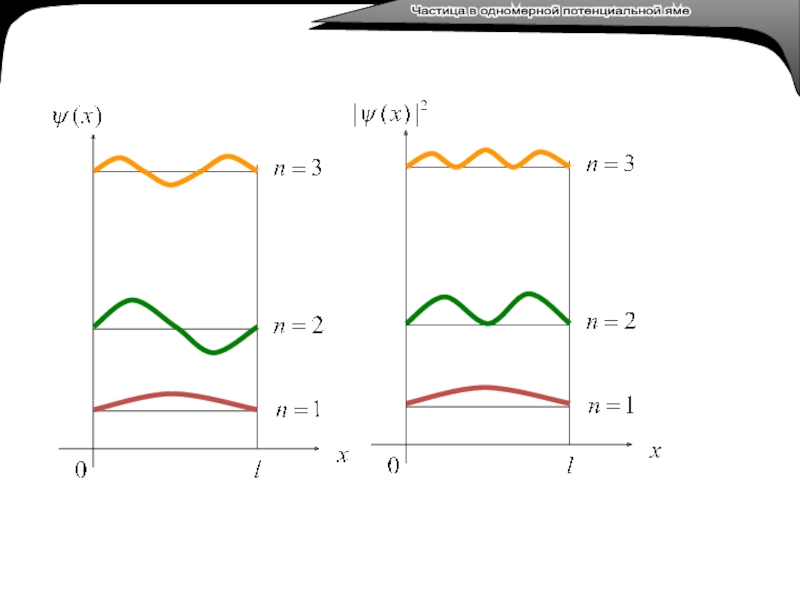
Получаем собственные волновые функции
И собственные значения энергии частицы в потенциальной яме,
Частица в одномерной потенциальной яме
Слайд 11Лекция 3. Тепловое излучение.
Лекция 3. Тепловое излучение.
Частица в одномерной
Частица в одномерной потенциальной яме
Слайд 13
Уравнение Шредингера имеет вид
Данное дифференциальное уравнение имеет решение только для определенных
- колебательное квантовое число, на которое накладывается правило отбора
Гармонический осциллятор
Слайд 14
Гармонический осциллятор
Гармонический осциллятор
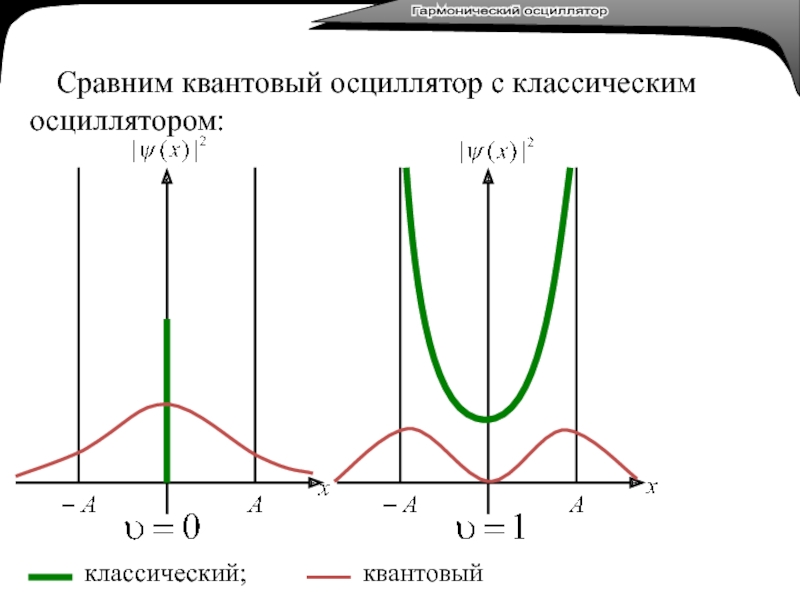
Сравним квантовый осциллятор с классическим
осциллятором:
классический;
квантовый
Слайд 21Воспользуемся достигнутыми результатами для того, чтобы рассчитать вероятность, с которой частица
Для упрощения расчетов положим что принципиально ничего не меняет. Тогда
Слайд 22Вероятность обнаружения частицы под потенциальным барьером в точке с координатой
Отношение называется плотностью
вероятности. Эффективной глубиной проникновения частицы называют такую глубину, на которой плотность вероятности уменьшается в раз.
Слайд 23Эффективная глубина проникновения частицы зависит от ее массы, энергии и высоты
Слайд 26
Коэффициент пропускания зависит от массы частицы, ширины и высоты потенциального барьера,
Туннельный эффект