Ulm
Stephan Schwantes
Institut für Fertigungstechnik und Werkstoffprüfung
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Werkstoffkunde презентация
Содержание
- 1. Werkstoffkunde
- 2. WK 1_2 Einführung Prof. S. Schwantes
- 3. WK 1_2 Einführung Prof. S. Schwantes
- 4. WK 1_2 Einführung Prof. S. Schwantes
- 5. WK 1_2 Einführung Prof. S. Schwantes
- 6. WK 1_2 Einführung Prof. S. Schwantes
- 7. WK 1_2 Einführung Prof. S. Schwantes
- 8. WK 1_2 Einführung Prof. S. Schwantes
- 9. WK 1_2 Einführung Prof. S. Schwantes
- 10. WK 1_2 Einführung Prof. S. Schwantes
- 11. WK 1_2 Einführung Prof. S. Schwantes
- 12. WK 1_2 Einführung Prof. S. Schwantes
- 13. WK 1_2 Einführung Prof. S. Schwantes
- 14. WK 1_2 Einführung Prof. S. Schwantes
- 15. WK 1_2 Einführung Prof. S. Schwantes
- 16. WK 1_2 Einführung Prof. S. Schwantes
- 17. WK 1_2 Einführung Prof. S. Schwantes
- 18. WK 1_2 Einführung Prof. S. Schwantes
- 19. WK 1_2 Einführung Prof. S. Schwantes
- 20. WK 1_2 Einführung Prof. S. Schwantes
- 21. WK 1_2 Einführung Prof. S. Schwantes
- 22. WK 1_2 Einführung Prof. S. Schwantes
- 23. WK 1_2 Einführung Prof. S. Schwantes
- 24. WK 1_2 Einführung Prof. S. Schwantes
- 25. WK 1_2 Einführung Prof. S. Schwantes
- 26. WK 1_2 Einführung Prof. S. Schwantes
- 27. WK 1_2 Einführung Prof. S. Schwantes
- 28. WK 1_2 Einführung Prof. S. Schwantes
- 29. WK 1_2 Einführung Prof. S. Schwantes
- 30. WK 1_2 Einführung Prof. S. Schwantes
- 31. WK 1_2 Einführung Prof. S. Schwantes
- 32. WK 1_2 Einführung Prof. S. Schwantes
- 33. WK 1_2 Einführung Prof. S. Schwantes
- 34. WK 1_2 Einführung Prof. S. Schwantes
- 35. WK 1_2 Einführung Prof. S. Schwantes
- 36. WK 1_2 Einführung Prof. S. Schwantes
- 37. WK 1_2 Einführung Prof. S. Schwantes
- 38. WK 1_2 Einführung Prof. S. Schwantes
- 39. WK 1_2 Einführung Prof. S. Schwantes
- 40. WK 1_2 Einführung Prof. S. Schwantes
- 41. WK 1_2 Einführung Prof. S. Schwantes
- 42. WK 1_2 Einführung Prof. S. Schwantes
- 43. WK 1_2 Einführung Prof. S. Schwantes
- 44. WK 1_2 Einführung Prof. S. Schwantes
- 45. WK 1_2 Einführung Prof. S. Schwantes
- 46. WK 1_2 Einführung Prof. S. Schwantes
- 47. WK 1_2 Einführung Prof. S. Schwantes
- 48. WK 1_2 Einführung Prof. S. Schwantes
- 49. WK 1_2 Einführung Prof. S. Schwantes
- 50. WK 1_2 Einführung Prof. S. Schwantes
- 51. WK 1_2 Einführung Prof. S. Schwantes
- 52. WK 1_2 Einführung Prof. S. Schwantes
- 53. WK 1_2 Einführung Prof. S. Schwantes
- 54. WK 1_2 Einführung Prof. S. Schwantes
- 55. WK 1_2 Einführung Prof. S. Schwantes
- 56. WK 1_2 Einführung Prof. S. Schwantes
WK 1_2 Einführung Prof. S. Schwantes ▶ Werkstoffkunde Wiederholung : Werkstoffgruppen hier nach Ashby Keramik anorganisch Kunststoffe organisch Metalle Verbundwerkstoffe
Слайд 1WK 1_2 Einführung
Prof. S. Schwantes
Vorlesung : Werkstoffkunde
im Bachelorstudiengang
„Maschinenbau“ der Hochschule
Слайд 2WK 1_2 Einführung
Prof. S. Schwantes
▶ Werkstoffkunde
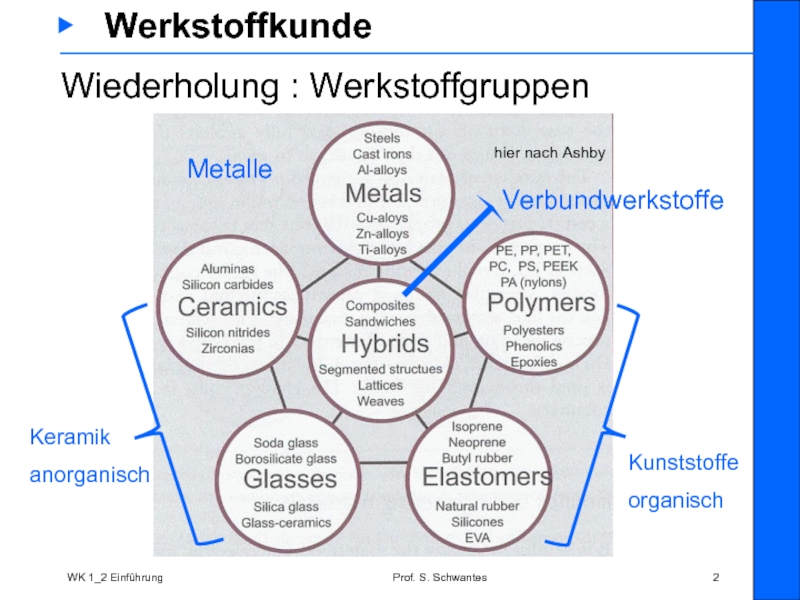
Wiederholung :
Werkstoffgruppen
hier nach Ashby
Keramik
anorganisch
Kunststoffe
organisch
Metalle
Verbundwerkstoffe
Слайд 4WK 1_2 Einführung
Prof. S. Schwantes
▶ Werkstoffkunde
Materialpreise
Die Materialpreise
verändern sich täglich
Rohstoffe werden an den Börsen gehandelt – Angebot und Nachfrage verändern die Preise laufend
Langfristig kann über die bekannten Lagerstätten und dem aktuellen Verbrauch ein Trend vorhergesagt werden
Rohstoffe werden an den Börsen gehandelt – Angebot und Nachfrage verändern die Preise laufend
Langfristig kann über die bekannten Lagerstätten und dem aktuellen Verbrauch ein Trend vorhergesagt werden
Слайд 5WK 1_2 Einführung
Prof. S. Schwantes
▶ Werkstoffkunde
Die Werkstoffauswahl
erfolgt in der Technik nach den Kriterien
Das Bauteil muss sicher seine Funktion erfüllen ↘ Definition der Funktion aus dem Pflichtenheft
Das Bauteil sollte so preiswert wie möglich sein, d. h. der Konstrukteur sucht nach wirtschaftlichen Lösungen
Abhängig von Losgrösse und Verarbeitungs-Know-How/Technologien
Das Bauteil muss sicher seine Funktion erfüllen ↘ Definition der Funktion aus dem Pflichtenheft
Das Bauteil sollte so preiswert wie möglich sein, d. h. der Konstrukteur sucht nach wirtschaftlichen Lösungen
Abhängig von Losgrösse und Verarbeitungs-Know-How/Technologien
Слайд 6WK 1_2 Einführung
Prof. S. Schwantes
▶ Werkstoffkunde
Die Werkstoffauswahl
erfolgt aufgrund der Eigenschaften
Dabei sind immer viele Eigenschaften zu berücksichtigen, d. h. ein relevantes Eigenschaftsprofil ist wichtig
Neben dem eigentlichen Materialpreis führen technische / physikalische / che-mische Eigenschaften zu Produktions- und Betriebskosten
Dabei sind immer viele Eigenschaften zu berücksichtigen, d. h. ein relevantes Eigenschaftsprofil ist wichtig
Neben dem eigentlichen Materialpreis führen technische / physikalische / che-mische Eigenschaften zu Produktions- und Betriebskosten
Слайд 7WK 1_2 Einführung
Prof. S. Schwantes
▶ Werkstoffkunde
Dazu ein
Beispiel
Stahlblech kostet ca. 1€/kg
Bei Blechen mit höherer Festigkeit reicht ev. eine geringere Blechstärke
Ein Blech mit höherer Festigkeit lässt sich aber viel schlechter verformen
• eventuell mehrere Umformschritte/ mehrere, teure Werkzeuge/ mehr Aus-schuß/ schlechtere Formgüte u. v. m.
Stahlblech kostet ca. 1€/kg
Bei Blechen mit höherer Festigkeit reicht ev. eine geringere Blechstärke
Ein Blech mit höherer Festigkeit lässt sich aber viel schlechter verformen
• eventuell mehrere Umformschritte/ mehrere, teure Werkzeuge/ mehr Aus-schuß/ schlechtere Formgüte u. v. m.
Слайд 8WK 1_2 Einführung
Prof. S. Schwantes
▶ Werkstoffkunde
Eigenschaften kann
man gliedern in
physikalische
chemische
technologische
wirtschaftliche
Eigenschaften
physikalische
chemische
technologische
wirtschaftliche
Eigenschaften
Слайд 9WK 1_2 Einführung
Prof. S. Schwantes
▶ Werkstoffkunde
Wirtschaftliche Eigenschaften
Materialkosten
Verfügbarkeit (z. B. welche Halbzeug- formate sind üblich)
Risiken (z. B. Anzahl der Anbieter, Anzahl der Rohstoffquellen)
Verfügbarkeit des Rohstoffes (z. B. ist Rohstoffe begrenzt vorhanden)
Verfügbarkeit (z. B. welche Halbzeug- formate sind üblich)
Risiken (z. B. Anzahl der Anbieter, Anzahl der Rohstoffquellen)
Verfügbarkeit des Rohstoffes (z. B. ist Rohstoffe begrenzt vorhanden)
Слайд 10WK 1_2 Einführung
Prof. S. Schwantes
▶ Werkstoffkunde
Technologische Eigenschaften
beschreiben die möglichen Bearbeitungs-techniken
Umformbarkeit
Schweißbarkeit/Fügbarkeit
Lackierbarkeit/Beschichtbarkeit
Zerspanbarkeit
Härtbarkeit
u. v. m.
Umformbarkeit
Schweißbarkeit/Fügbarkeit
Lackierbarkeit/Beschichtbarkeit
Zerspanbarkeit
Härtbarkeit
u. v. m.
Слайд 11WK 1_2 Einführung
Prof. S. Schwantes
▶ Werkstoffkunde
Chemische Eigenschaften
beständig gegen Lösungsmittel
giftig / toxisch
korrosionsbeständig
beständig gegen Oxidation
beständig gegen UV-Licht
u. v. m.
giftig / toxisch
korrosionsbeständig
beständig gegen Oxidation
beständig gegen UV-Licht
u. v. m.
Слайд 12WK 1_2 Einführung
Prof. S. Schwantes
▶ Werkstoffkunde
Physikalische Eigenschaften
mechanische Eigenschaften
magnetische Eigenschaften
elektrische Eigenschaften
optische Eigenschaften
thermischen Eigenschaften
………
magnetische Eigenschaften
elektrische Eigenschaften
optische Eigenschaften
thermischen Eigenschaften
………
Слайд 13WK 1_2 Einführung
Prof. S. Schwantes
▶ Werkstoffkunde
Mechanische Eigenschaften
Zug- / Druck- / Biege- / Torsionsfestigkeit
Steifigkeit
Zähigkeit
Härte
Ermüdungseigenschaften
Dämpfung
………
Steifigkeit
Zähigkeit
Härte
Ermüdungseigenschaften
Dämpfung
………
Слайд 14WK 1_2 Einführung
Prof. S. Schwantes
▶ Werkstoffkunde
Mechanische Eigenschaften
in
der Mechanik geht es um Kräfte und Momente
unter den mechanischen Eigenschaften versteht man die Reaktion des Materials auf äußere Kräfte und Momente ( allge-mein die Belastungen )
Diese Reaktionen können Verformungen, Brüche oder Energieumwandlungen sein
unter den mechanischen Eigenschaften versteht man die Reaktion des Materials auf äußere Kräfte und Momente ( allge-mein die Belastungen )
Diese Reaktionen können Verformungen, Brüche oder Energieumwandlungen sein
Слайд 15WK 1_2 Einführung
Prof. S. Schwantes
▶ Werkstoffkunde
Mechanische Eigenschaften
Um
einen Körper belasten zu können, muss er stabil gelagert werden, d. h. definiert festgehalten werden
Ein von außen belasteter Körper hat im Inneren eine Spannungsverteilung
Ein belasteter Körper zeigt von außen eine Verformung, d. h. eine Gestaltänderung
Die Verformung führt im Inneren zu einer Dehnungsverteilung
Ein von außen belasteter Körper hat im Inneren eine Spannungsverteilung
Ein belasteter Körper zeigt von außen eine Verformung, d. h. eine Gestaltänderung
Die Verformung führt im Inneren zu einer Dehnungsverteilung
Слайд 16WK 1_2 Einführung
Prof. S. Schwantes
▶ Werkstoffkunde
Spannungen
Spannungen haben
die Einheit Kraft / Fläche
Spannungen sind gerichtete Größen ( = Vektoren)
Spannungen sind gerichtete Größen ( = Vektoren)
Spannungen im Inneren kann man nicht sehen & messen, aber an gedachten Schnitten berechnen, d. h. es werden Gleichgewichtsbedingungen erfüllt
Слайд 17WK 1_2 Einführung
Prof. S. Schwantes
▶ Werkstoffkunde
Spannungen
Spannungen im
Inneren kann man nicht sehen & messen, aber an gedachten Schnitten berechnen
Dabei nutzt man die Gleichgewichtsbedingungen aus, was in der TM weiter vertieft wird
Dabei nutzt man die Gleichgewichtsbedingungen aus, was in der TM weiter vertieft wird
Ändern wir die Schnittebene, so werden sich andere Spannungswerte ergeben, da sich die Bezugsfläche ändert!
Слайд 18WK 1_2 Einführung
Prof. S. Schwantes
▶ Werkstoffkunde
Spannungen
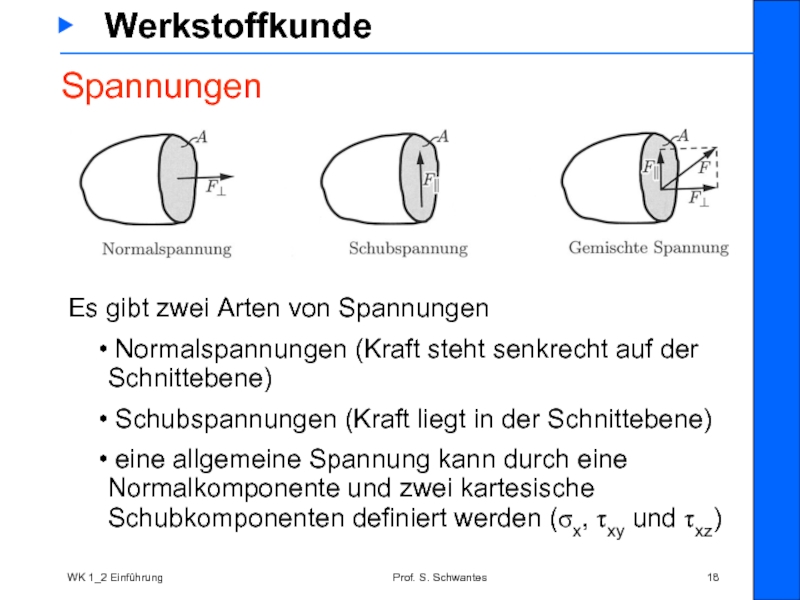
Es gibt
zwei Arten von Spannungen
Normalspannungen (Kraft steht senkrecht auf der Schnittebene)
Schubspannungen (Kraft liegt in der Schnittebene)
eine allgemeine Spannung kann durch eine Normalkomponente und zwei kartesische Schubkomponenten definiert werden (σx, τxy und τxz)
Normalspannungen (Kraft steht senkrecht auf der Schnittebene)
Schubspannungen (Kraft liegt in der Schnittebene)
eine allgemeine Spannung kann durch eine Normalkomponente und zwei kartesische Schubkomponenten definiert werden (σx, τxy und τxz)
Слайд 19WK 1_2 Einführung
Prof. S. Schwantes
▶ Werkstoffkunde
Spannungen
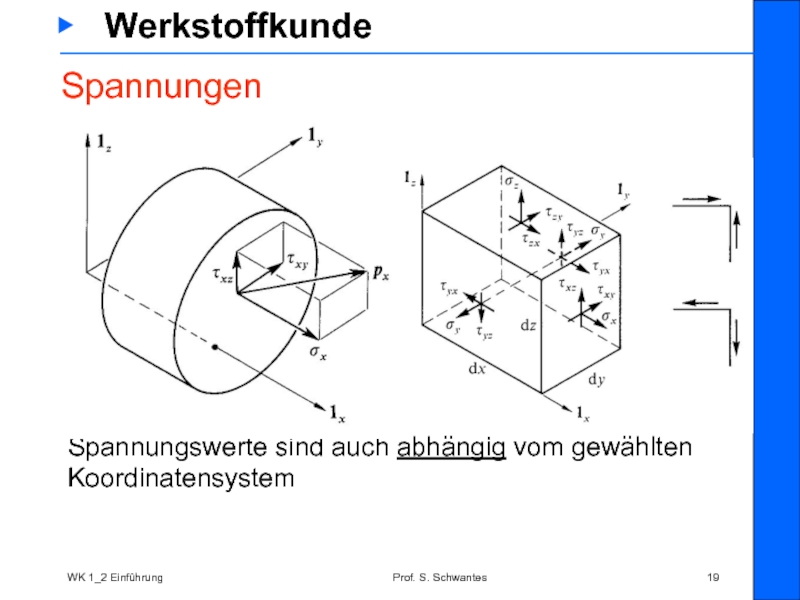
Spannungswerte sind
auch abhängig vom gewählten Koordinatensystem
Слайд 20WK 1_2 Einführung
Prof. S. Schwantes
▶ Werkstoffkunde
Spannungen
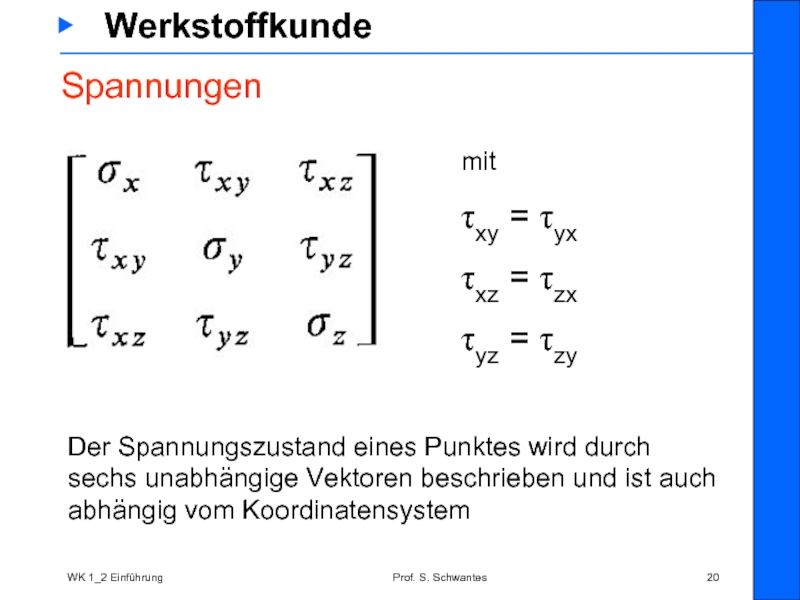
Der Spannungszustand
eines Punktes wird durch sechs unabhängige Vektoren beschrieben und ist auch abhängig vom Koordinatensystem
mit
τxy = τyx
τxz = τzx
τyz = τzy
Слайд 21WK 1_2 Einführung
Prof. S. Schwantes
▶ Werkstoffkunde
Spannungen
Wir wollen
zunächst nur einfache (= ein-achsige) Spannungszustände betrachten
Der allgemeine Fall von beliebigen Spannungen im Raum (3D) ist sehr kompliziert
Der allgemeine Fall von beliebigen Spannungen im Raum (3D) ist sehr kompliziert
Слайд 22WK 1_2 Einführung
Prof. S. Schwantes
▶ Werkstoffkunde
Verformung und
Dehnung
Die einachsige Normalspannung führt zu einer Verlängerung der Stabes um ΔL=L(F)-LO
Wenn Spannung und Verformung gleichförmig ist ( = homogen ), dann ist die Längsdehnung ε
ε = ΔL / LO
ΔL
L(F)
LO
Слайд 23WK 1_2 Einführung
Prof. S. Schwantes
▶ Werkstoffkunde
Verformung und
Dehnung
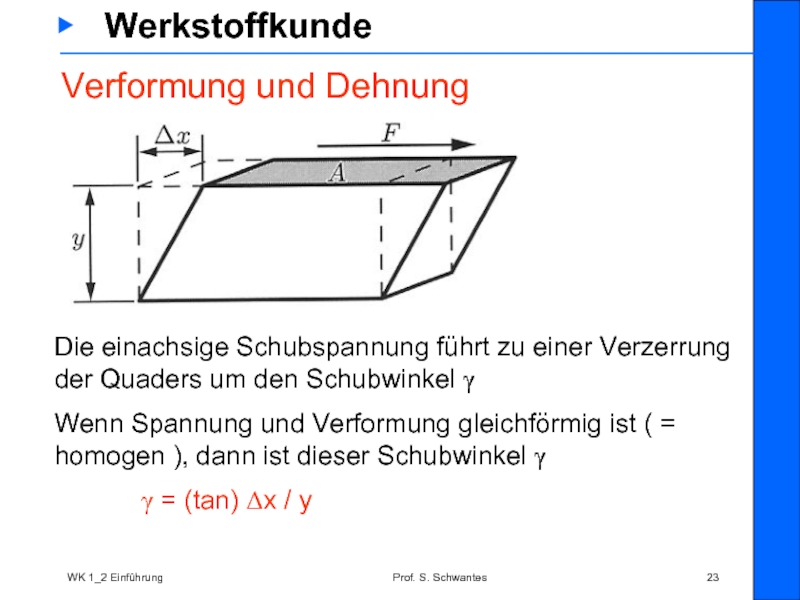
Die einachsige Schubspannung führt zu einer Verzerrung der Quaders um den Schubwinkel γ
Wenn Spannung und Verformung gleichförmig ist ( = homogen ), dann ist dieser Schubwinkel γ
γ = (tan) Δx / y
Слайд 24WK 1_2 Einführung
Prof. S. Schwantes
▶ Werkstoffkunde
Verformung und
Dehnung
Die Verformung ist die Integration der Dehnungen und umgekehrt
Wir betrachten in der Ebene x-y die Verschiebungsfunktionen u in x-Richtung und v in y-Richtung
Jedem Punkt (x,y) wird also ein Verschiebungsvektor (u,v) zugeordnet
Die Verformung ist die Integration der Dehnungen und umgekehrt
Wir betrachten in der Ebene x-y die Verschiebungsfunktionen u in x-Richtung und v in y-Richtung
Jedem Punkt (x,y) wird also ein Verschiebungsvektor (u,v) zugeordnet
Слайд 26WK 1_2 Einführung
Prof. S. Schwantes
▶ Werkstoffkunde
Verformung und
Dehnung
Dehnungen als partielle Ableitung der Verschiebungsfunktion
Dehnungen als partielle Ableitung der Verschiebungsfunktion
Слайд 27WK 1_2 Einführung
Prof. S. Schwantes
▶ Werkstoffkunde
Verformung und
Dehnung
Die Verformung ist im allgemeinen 3D-Fall wieder ein symmetrischer 3x3 Tensor mit sechs unabhängigen gerichteten Größen
Die Verformung ist im allgemeinen 3D-Fall wieder ein symmetrischer 3x3 Tensor mit sechs unabhängigen gerichteten Größen
Слайд 28WK 1_2 Einführung
Prof. S. Schwantes
▶ Werkstoffkunde
Werkstoffgesetze
Wie sich
ein Werkstoff mechanisch verhält kann man durch Werkstoffgesetze beschreiben
Diese sind die mathematische Kopplung von Spannungen und Dehnungen
In der allgemeinen Form heißt das, ein Operator berechnet aus dem Spannungstensor den Dehnungstensor
Diese sind die mathematische Kopplung von Spannungen und Dehnungen
In der allgemeinen Form heißt das, ein Operator berechnet aus dem Spannungstensor den Dehnungstensor
Слайд 29WK 1_2 Einführung
Prof. S. Schwantes
▶ Werkstoffkunde
Werkstoffgesetze
es gibt
drei Grundverhaltensarten und viele Kombinationen und Sonderfälle
elastisches Verhalten
plastisches Verhalten
viskoses Verhalten
elastisches Verhalten
plastisches Verhalten
viskoses Verhalten
Слайд 30WK 1_2 Einführung
Prof. S. Schwantes
▶ Werkstoffkunde
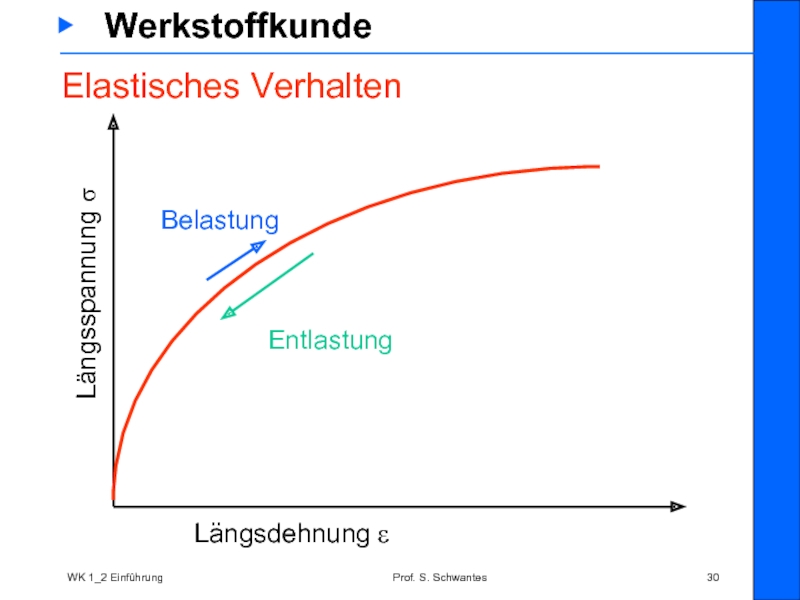
Elastisches Verhalten
Längsspannung σ
Längsdehnung ε
Belastung
Entlastung
Слайд 31WK 1_2 Einführung
Prof. S. Schwantes
▶ Werkstoffkunde
Elastisches Verhalten
Be- und Entlastung hat gleiche Funktion ε = f(σ)
Das Material speichert die mechanische Energie und gibt sie auch in mechanischer Form wieder ab wie bei einer Feder
Die Verformung ist reversibel, d. h. sie geht auf 0 zurück wenn die Belastung komplett abgebaut wird
Das Material speichert die mechanische Energie und gibt sie auch in mechanischer Form wieder ab wie bei einer Feder
Die Verformung ist reversibel, d. h. sie geht auf 0 zurück wenn die Belastung komplett abgebaut wird
Слайд 32WK 1_2 Einführung
Prof. S. Schwantes
▶ Werkstoffkunde
Elastisches Verhalten
Sonderformen sind
ideal elastisch
die Dämpfung ist nicht vorhanden, die Energie wird vollständig zurückgegeben
linear elastisch
Dehnungen sind der Spannung proportional
Слайд 33WK 1_2 Einführung
Prof. S. Schwantes
▶ Werkstoffkunde
Elastisches Verhalten
Viele Materialien, vor allem Metalle im elastischen Bereich sind näherungsweise linear elastisch
Es ergeben sich dann zwei Proportionalitätskonstanten, die als elastische Materialkonstanten auftreten
E = σ / ε E = Elastizitätsmodul
oder kurz E-Modul
G = τ / γ G = Schubmodul
Слайд 34WK 1_2 Einführung
Prof. S. Schwantes
▶ Werkstoffkunde
Elastisches Verhalten
E = σ / ε E = Elastizitätsmodul
oder kurz E-Modul
G = τ / γ G = Schubmodul
Wichtig für die eigene Anwendung :
Diese Quotienten gelten nur im elastischen Bereich und dürfen nicht allgemein angewendet werden, z. B. aus einem Wertepaar σ und ε aus dem Zugversuch
Слайд 35WK 1_2 Einführung
Prof. S. Schwantes
▶ Werkstoffkunde
Elastisches Verhalten
Aus den beiden elastischen Materialkonstanten ergibt sich eine dritte Konstante, die Querkontraktionszahl μ
G = E / { 2 · (1 + μ)}
Der Wert wird auch häufig Poisson-Zahl genannt und manchmal mit ν abgekürzt
Слайд 36WK 1_2 Einführung
Prof. S. Schwantes
▶ Werkstoffkunde
Elastisches Verhalten
Die Querkontraktionszahl μ gibt an, wie sich die Querdehnung zur Längsdehnung bei elastischem Verhalt ergibt
εlängs = - μ · εquer
Der Wert beträgt bei vielen Metallen ungefähr 0,3
Слайд 37WK 1_2 Einführung
Prof. S. Schwantes
▶ Werkstoffkunde
Elastisches Verhalten
Einige typische Werte für E und G in GPa
Diamant 1000 450
Al2O3 390 180
Stahl 210 80
Alu 70 27
PMMA 3 1,2
Holz ⊥ zur Faser 1 0,4
Holz || zur Faser 10 4
→ Holz ist ein anisotroper Werkstoff
Слайд 38WK 1_2 Einführung
Prof. S. Schwantes
▶ Werkstoffkunde
Elastisches Verhalten
Anisotropie
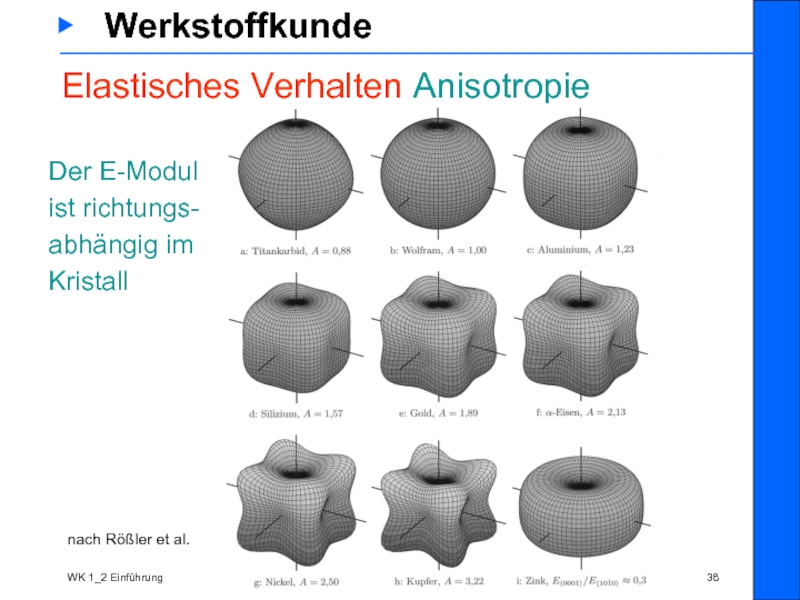
nach Rößler et al.
Der E-Modul
ist richtungs-
abhängig im
Kristall
Слайд 39WK 1_2 Einführung
Prof. S. Schwantes
▶ Werkstoffkunde
Elastisches Verhalten
nach
Rößler et al.
nach Ashby
Слайд 40WK 1_2 Einführung
Prof. S. Schwantes
▶ Werkstoffkunde
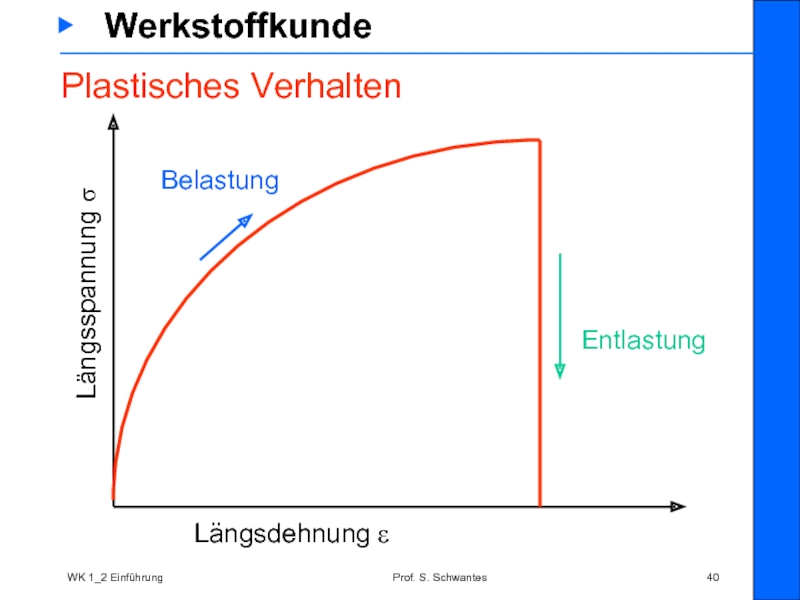
Plastisches Verhalten
Längsspannung σ
Längsdehnung ε
Belastung
Entlastung
Слайд 41WK 1_2 Einführung
Prof. S. Schwantes
▶ Werkstoffkunde
Plastisches Verhalten
Be- und Entlastung folgt mit unterschiedlichen Funktionen
Bei der Belastung wird mechanische Arbeit in das Bauteil eingebracht
Bei der Entlastung wird keine Energie mechanisch abgegeben, sie wurde z. B. in Wärme umgesetzt
Слайд 42WK 1_2 Einführung
Prof. S. Schwantes
▶ Werkstoffkunde
Plastisches Verhalten
Durch die plastische Verformung wird das Bauteil bleibend verformt •Umformtechnik
Plastische Verformung ist normaler-weise im Betrieb unerwünscht •Formänderung der Bauteile
Plastische Verformung wird benutzt um im Crashfall Energie aufzunehmen •Energieumwandlung z. B. in Wärme
Слайд 43WK 1_2 Einführung
Prof. S. Schwantes
▶ Werkstoffkunde
Plastisches Verhalten
Sonderfälle
idealplastisches Verhalten
Material fließt ab eine bestimmten Spannung ohne Verfestigung,
d. h. bei konstanter Spannung
Dieses Material kann nur druckverformt werden, Zugspannung führen zur lokalen Einschnürung (Materialausdünnung und nachfolgendem Bruch)
Слайд 44WK 1_2 Einführung
Prof. S. Schwantes
▶ Werkstoffkunde
Idealplastisches Verhalten
Längsspannung
σ
Längsdehnung ε
Belastung
Entlastung
ohne Verfestigung
= ideal plastisch
Sonderfall!!!
mit Verfestigung (Normalfall)
Слайд 45WK 1_2 Einführung
Prof. S. Schwantes
▶ Werkstoffkunde
Viskoses Verhalten
Bisher war die Beziehung zwischen Spannung und Dehnung zeitunabhängig
Je nach Temperatur, Belastung und Werkstoff gibt es aber ein Verhalten, bei dem die Dehnungen ständig zunehmen, wenn die Spannungen einen Mindestwert übersteigen
Слайд 46WK 1_2 Einführung
Prof. S. Schwantes
▶ Werkstoffkunde
Viskoses Verhalten
Bei diesem Verhalten kann die Dehnung als Integration einer Dehnungsrate berechnet werden
Die Dehnungsrate ist die Ableitung der Dehnung nach der Zeit
dε / dt = ε
analog zu d f(x) / d x = f´(x)
Слайд 48WK 1_2 Einführung
Prof. S. Schwantes
▶ Werkstoffkunde
Viskoses Verhalten
Kriechen
log Zeit
log Zeit
Слайд 49WK 1_2 Einführung
Prof. S. Schwantes
▶ Werkstoffkunde
Viskoses Verhalten
Kriechen
Dieses Verhalten wird als thermisch aktiviertes Verhalten, Kriechen oder Relaxieren bezeichnet
Im Bereich I findet ein Einschwingen statt
Im Bereich II erfolgt stationäres Kriechen mit ε ≈ σn ⋅ exp (- Q / R·T) berechenbar
Im Bereich III ist der Werkstoff irreparabel geschädigt und sollte nicht mehr benutzt werden
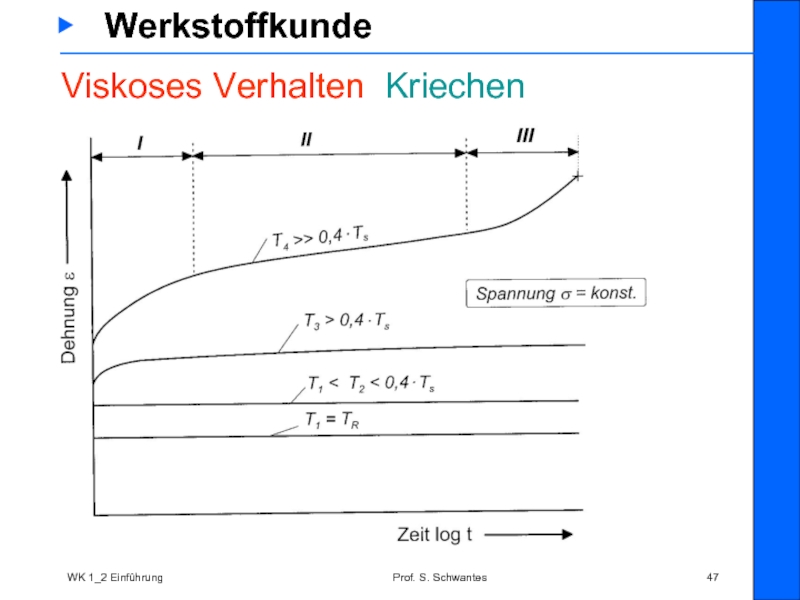
Dieses Verhalten wird als thermisch aktiviertes Verhalten, Kriechen oder Relaxieren bezeichnet
Im Bereich I findet ein Einschwingen statt
Im Bereich II erfolgt stationäres Kriechen mit ε ≈ σn ⋅ exp (- Q / R·T) berechenbar
Im Bereich III ist der Werkstoff irreparabel geschädigt und sollte nicht mehr benutzt werden
Слайд 50WK 1_2 Einführung
Prof. S. Schwantes
▶ Werkstoffkunde
Viskoses Verhalten
Kriechen
Relaxieren bezeichnet den Abfall der Spannungen bei konstant gehaltener Dehnung
Dies tritt häufig bei Schrauben-verbindungen auf
Dadurch reduziert sich die Vorspannung
Schrauben können sich lockern
Flansche werden undicht
Relaxieren bezeichnet den Abfall der Spannungen bei konstant gehaltener Dehnung
Dies tritt häufig bei Schrauben-verbindungen auf
Dadurch reduziert sich die Vorspannung
Schrauben können sich lockern
Flansche werden undicht
Слайд 51WK 1_2 Einführung
Prof. S. Schwantes
▶ Werkstoffkunde
Viskoses Verhalten
Kriechen
Kriechen wird experimentell im Zeitstandversuch ermittelt
Hier wird eine Zugprobe über längere Zeit mit einer konstanten Spannung belastet und die Dehnung ε wird über diese gesamte Zeit gemessen
Die gewonnene Information kann als Zeitstandfestigkeit oder als Zeitstanddehnung dargestellt werden
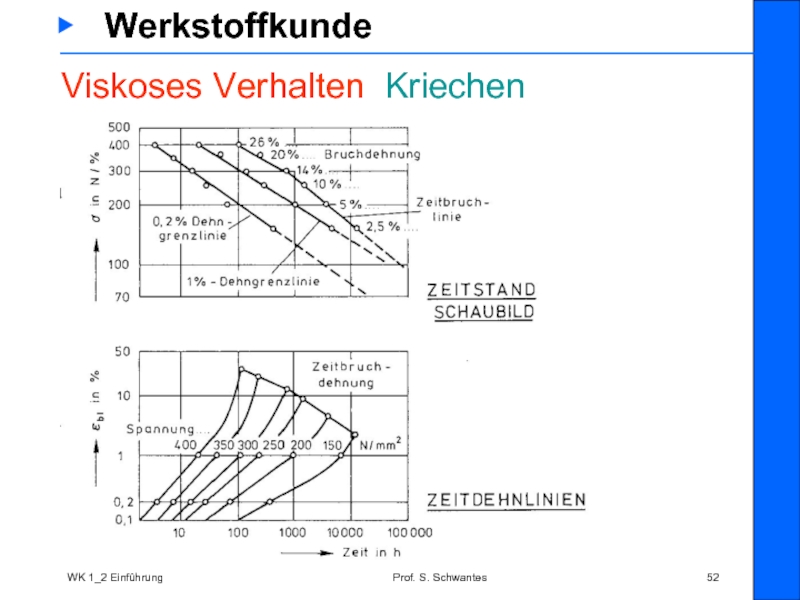
Kriechen wird experimentell im Zeitstandversuch ermittelt
Hier wird eine Zugprobe über längere Zeit mit einer konstanten Spannung belastet und die Dehnung ε wird über diese gesamte Zeit gemessen
Die gewonnene Information kann als Zeitstandfestigkeit oder als Zeitstanddehnung dargestellt werden
Слайд 54WK 1_2 Einführung
Prof. S. Schwantes
▶ Werkstoffkunde
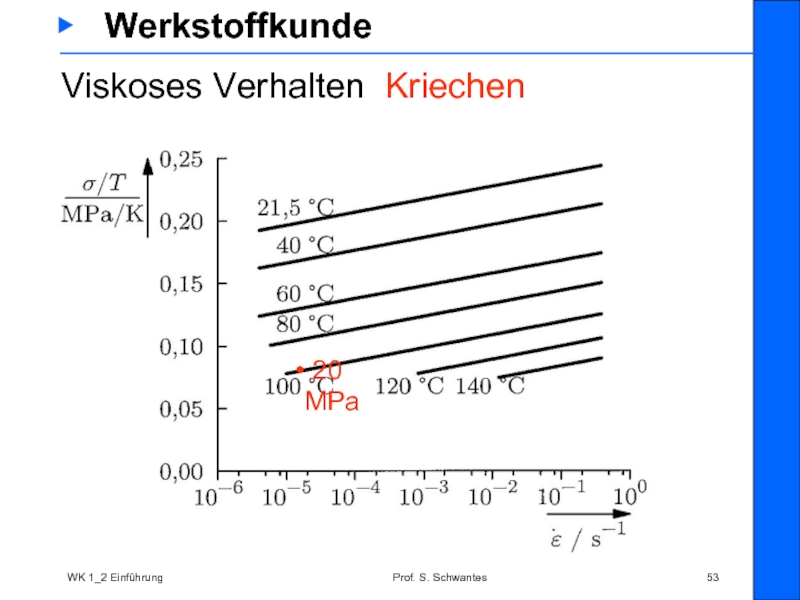
Viskoses Verhalten
Kriechen
Viskoses Verhalten tritt schon bei niedrigen Temperaturen wie Raumtemperatur bei Kunststoffen und Blei auf
Bei Metallen ist die Grenze oftmals bei T > (0.4 - 0.6) TS
(TS = Schmelztemperatur in K)
Dieser Bereich heißt
holonome Temperatur
Viskoses Verhalten tritt schon bei niedrigen Temperaturen wie Raumtemperatur bei Kunststoffen und Blei auf
Bei Metallen ist die Grenze oftmals bei T > (0.4 - 0.6) TS
(TS = Schmelztemperatur in K)
Dieser Bereich heißt
holonome Temperatur
Слайд 55WK 1_2 Einführung
Prof. S. Schwantes
▶ Werkstoffkunde
Bei allen
Materialien treten alle Verhalten überlagert auf
Bei Metallen dominiert bei niedrigen Temperaturen elastisches und elasto-plastisches Verhalten
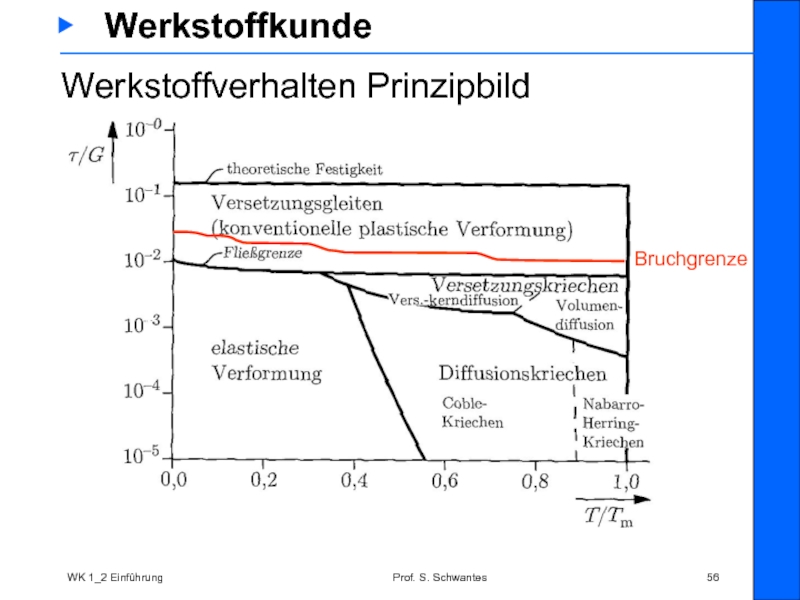
Bei hohen Temperaturen wird Kriechen immer dominanter und muss auch rechnerisch bei der Bauteilauslegung berücksichtigt werden
Bei Metallen dominiert bei niedrigen Temperaturen elastisches und elasto-plastisches Verhalten
Bei hohen Temperaturen wird Kriechen immer dominanter und muss auch rechnerisch bei der Bauteilauslegung berücksichtigt werden
Слайд 56WK 1_2 Einführung
Prof. S. Schwantes
▶ Werkstoffkunde
Werkstoffverhalten Prinzipbild
Bruchgrenze
