- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Введение в курс ГГД. Основные понятия и предмет изучения курса ГГД презентация
Содержание
- 1. Введение в курс ГГД. Основные понятия и предмет изучения курса ГГД
- 2. План курса ГГД Лекции (1 раз в
- 3. Литература к курсу ГГД Г.С. Самойлович «Гидрогазодинамика»
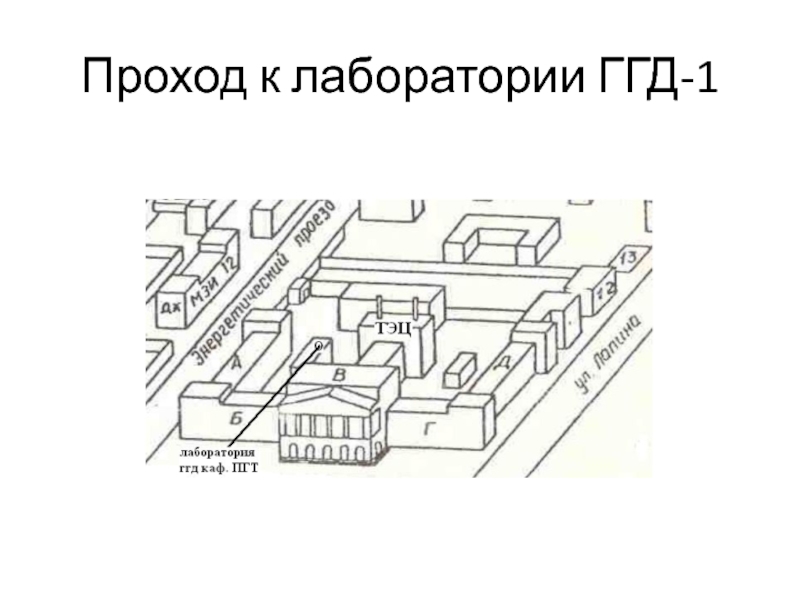
- 4. Проход к лаборатории ГГД-1
- 5. Проход к лаборатории ГГД-2
- 6. Курс ГГД Предмет гидрогазодинамики – часть
- 7. Основные задачи гидроаэромеханики Жидкость (газ) в покое
- 8. Параметры, характеризующие жидкую или газообразную среду в
- 9. Примеры силового взаимодействия жидких (газообразных) и твердых
- 10. Молекулярная структура и агрегатное состояние вещества (l
- 11. МЕХАНИКА СПЛОШНЫХ СРЕД: Механика жидкости и газа
- 12. Вязкость определяется касательными (сдвиговыми) напряжениями (τ) и коэффициентом динамической вязкости (μ)
- 13. Идеальная жидкость Малость величины μ для технически
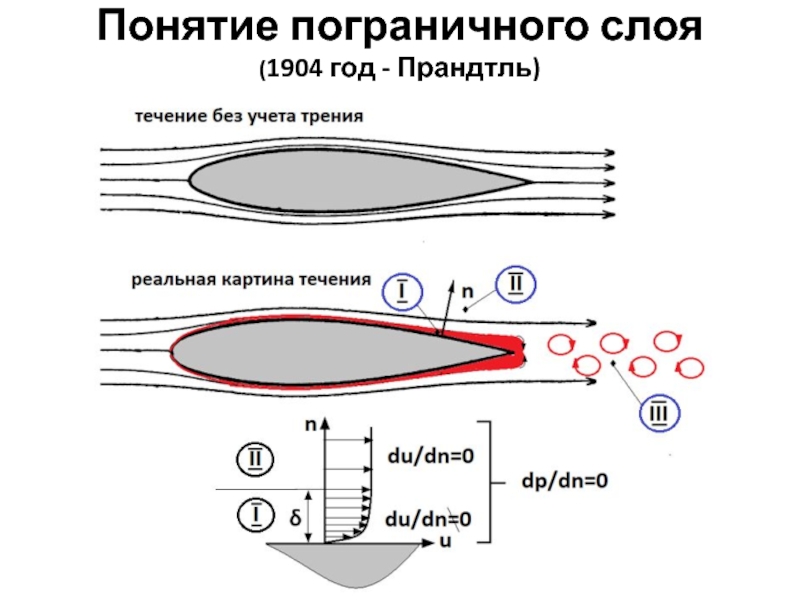
- 14. Понятие пограничного слоя (1904 год - Прандтль)
- 15. Свойства газов Справедливо уравнение состояния для идеального
- 16. Особенности применения законов механики к изучению движений
- 17. Классификация сил, действующих в жидкости В классической
- 18. Классификация сил, действующих в жидкости Результат взаимодействия
- 19. Силы в покоящейся жидкости В покоящейся жидкости
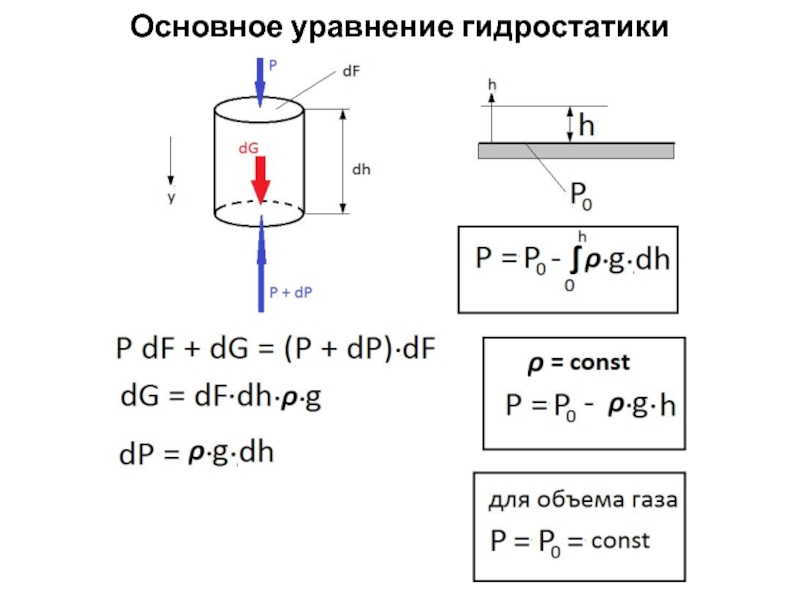
- 20. Основное уравнение гидростатики
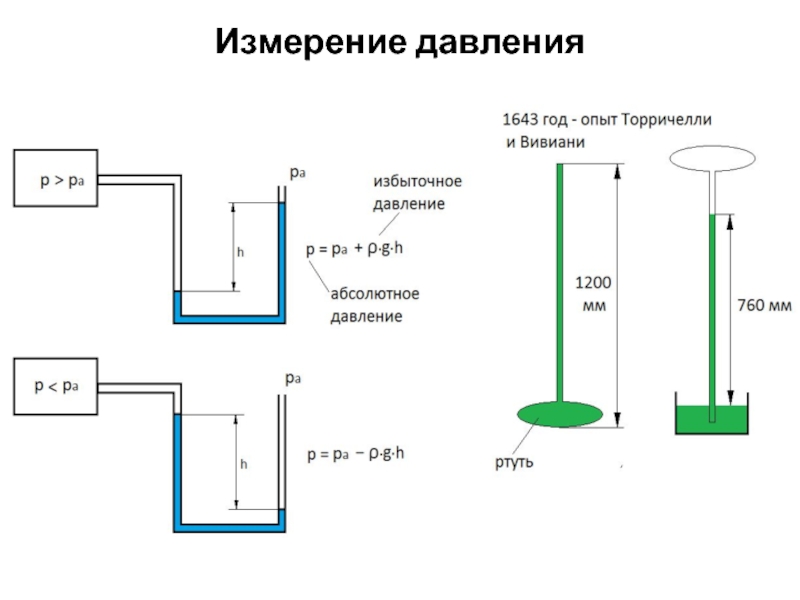
- 21. Измерение давления
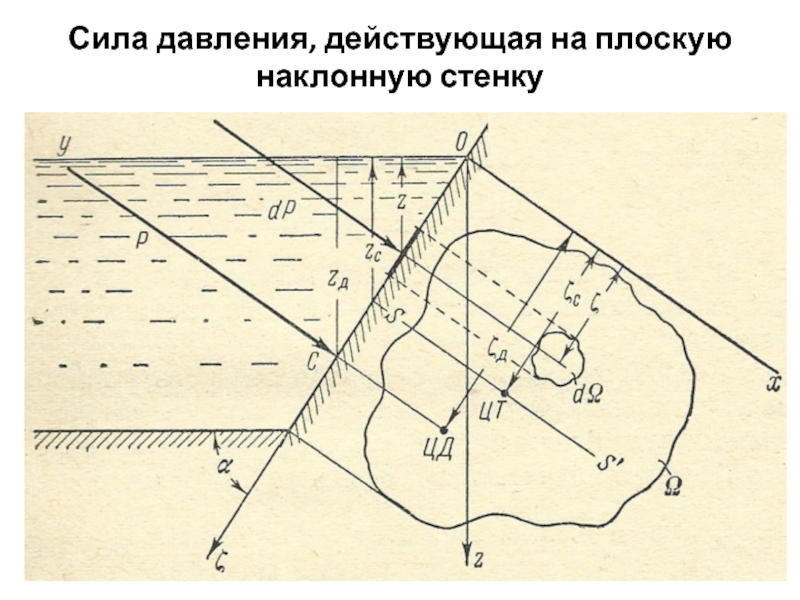
- 22. Сила давления, действующая на плоскую наклонную стенку
- 23. «Полная сила избыточного давления жидкости на плоскую
Слайд 1
Введение в курс ГГД.
Основные понятия и предмет изучения курса ГГД.
Лекция №
2017
Дмитриев С.С.
Слайд 2План курса ГГД
Лекции (1 раз в неделю)
Практические занятия (1 раз в
Типовые расчеты (5) по плану БАРС с оценкой по 100-балльной системе
Лабораторные работы (3)
Экзамен (письменный) – решение задач
Слайд 3Литература к курсу ГГД
Г.С. Самойлович «Гидрогазодинамика» 1990.
В.В. Нитусов, В.Г. Грибин «Гидрогазодинамика.
В.В. Нитусов, В.Г. Грибин «МЖГ. Сборник задач». 2009.
Зарянкин А.Е. Механика несжимаемых и сжимаемых жидкостей. М. Изд. дом МЭИ. 2014.
Т.Е. Фабер. Гидроаэродинамика. М. 2001
Л.Г. Лойцянский. Механика жидкости и газа. М. 1978.
Слайд 6Курс ГГД
Предмет гидрогазодинамики – часть общего курса гидроаэромеханики,
Изучает законы движения
Гидроаэромеханика – более общий предмет, т.к. включает еще гидростатику.
Слайд 7Основные задачи гидроаэромеханики Жидкость (газ) в покое – гидростатика, жидкость (газ) движется
Определение распределения характерных параметров внутри некоторого выделенного объема жидкости или газа.
2. Определение силового взаимодействия между жидкостью или газом и твердыми телами, находящимися внутри некоторого выделенного объема жидкости или газа или окружающими его.
Слайд 8Параметры, характеризующие жидкую или газообразную среду в данной точке
Скорость -
Массовая плотность – ρ=lim(m/V) при V→0, размерность [кг/м3] , скаляр.
Давление - р, размерность [Па = н/м2], скаляр.
Температура – Т, размерность [К].
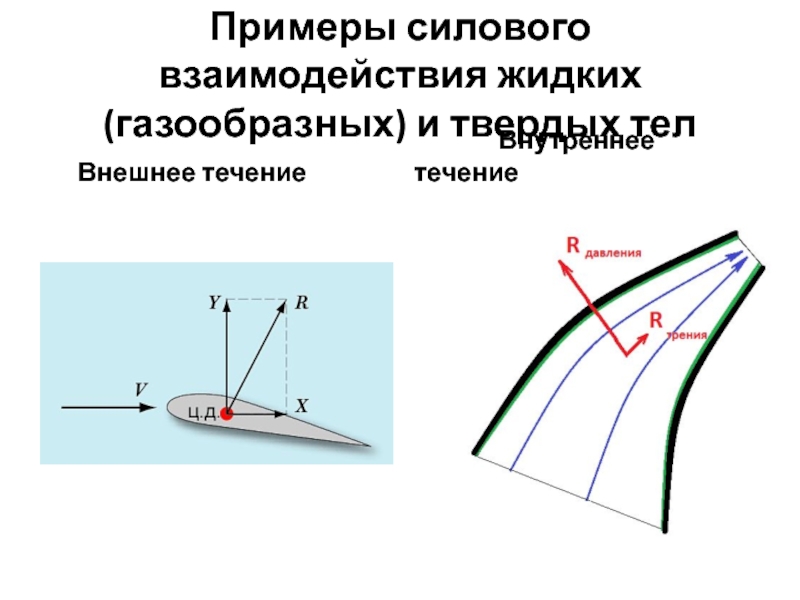
Слайд 9Примеры силового взаимодействия жидких (газообразных) и твердых тел
Внешнее
Внутреннее течение
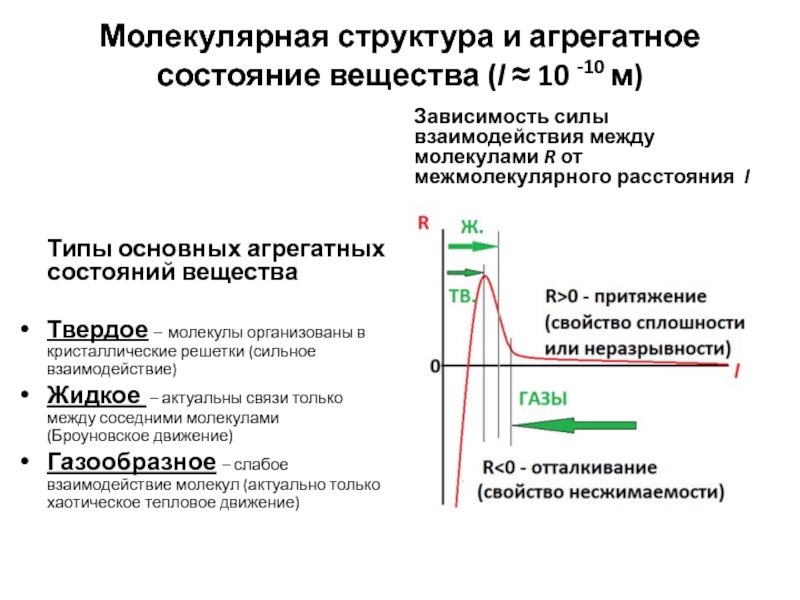
Слайд 10Молекулярная структура и агрегатное состояние вещества (l ≈ 10 -10 м)
Типы
Твердое – молекулы организованы в кристаллические решетки (сильное взаимодействие)
Жидкое – актуальны связи только между соседними молекулами (Броуновское движение)
Газообразное – слабое взаимодействие молекул (актуально только хаотическое тепловое движение)
Зависимость силы взаимодействия между молекулами R от межмолекулярного расстояния l
Слайд 11МЕХАНИКА СПЛОШНЫХ СРЕД:
Механика жидкости и газа ↔ Механика твердого тела
Общие свойства
Сплошность;
Текучесть;
Свойство внутреннего трения (вязкость) – способность оказывать сопротивление деформации при движении жидкости (газа) и отсутствие этого сопротивления в состоянии равновесия (покоя) – можно проверить опытом с рукой, движущейся в воде.
Различия жидкостей и газов
Сжимаемость (капельная жидкость и газ). Существенно сказывается на характере движения только при значительных скоростях газового потока;
Наличие свободной границы у капельных жидкостей и отсутствие таковой у газов при заполнении какого-то объема.
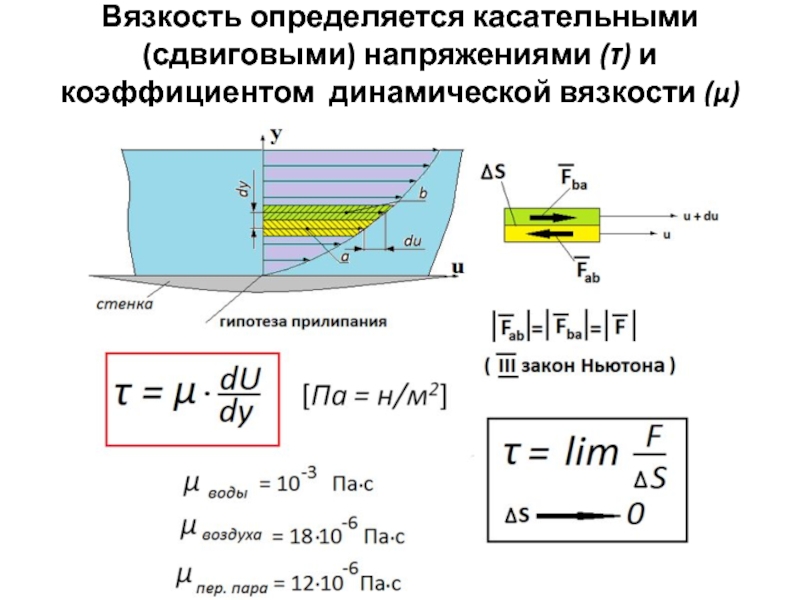
Слайд 12Вязкость определяется касательными (сдвиговыми) напряжениями (τ) и коэффициентом динамической вязкости (μ)
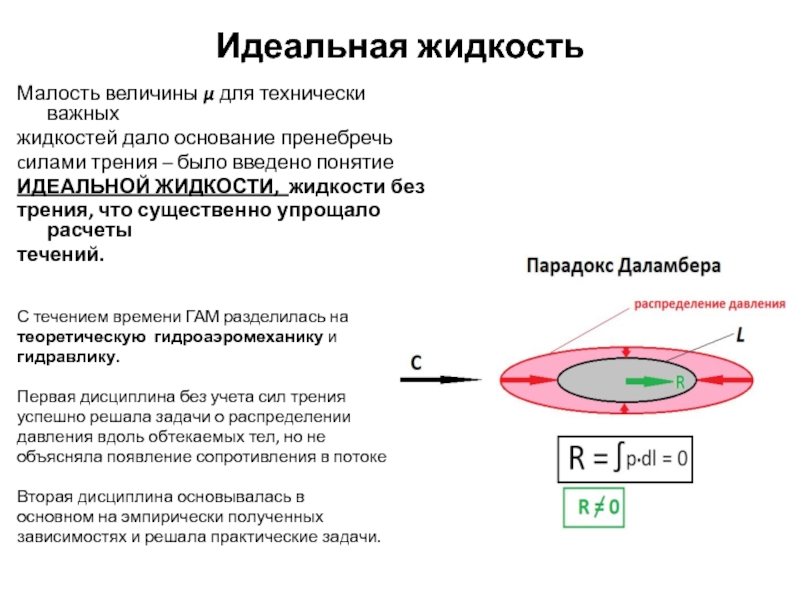
Слайд 13Идеальная жидкость
Малость величины μ для технически важных
жидкостей дало основание пренебречь
cилами трения – было введено понятие
ИДЕАЛЬНОЙ ЖИДКОСТИ, жидкости без
трения, что существенно упрощало расчеты
течений.
С течением времени ГАМ разделилась на
теоретическую гидроаэромеханику и
гидравлику.
Первая дисциплина без учета сил трения
успешно решала задачи о распределении
давления вдоль обтекаемых тел, но не
объясняла появление сопротивления в потоке.
Вторая дисциплина основывалась в
основном на эмпирически полученных
зависимостях и решала практические задачи.
Слайд 15Свойства газов
Справедливо уравнение состояния для идеального газа
p/ρ = R·T
R = (cp – cv ) [дж/(кг·К)]
Rвозд. = 287,1 дж/(кг·К) Rпер.пара. = 464 дж/(кг·К)
R μ = 8314 [дж/(кмоль·К)] – универсальная газовая постоянная
R = Rμ /mμ [дж/(кмоль·К)] / [кг/кмоль] = [дж/(кг·К)]
При сжатии газов Тг↑; при расширении Тг↓
Быстропротекающий процесс сжатия и расширения при движении газов проходит без теплообмена с окружающий средой - процесс адиабатический , и с учетом того, что газ идеальный:
p/ρk = const
k = cp / cv k возд. = 1,4 k пер.пара. = 1,3
Слайд 16Особенности применения законов механики к изучению движений жидкостей и газов
1. Пренебречь изменением параметров внутри этого объема.
2. Не учитывать взаимодействие на молекулярном уровне.
3. Вместо физических величин, сосредоточенных в точке, как в классической механике Ньютона, рассматриваются функции распределения этих величин (р, с, ρ, Т) в пространстве, занимаемом жидкостью (газом).
4. Эти функции считаются (как правило) непрерывными и дифференцируемыми, что позволяет применять анализ бесконечно малых (методы мат. анализа)
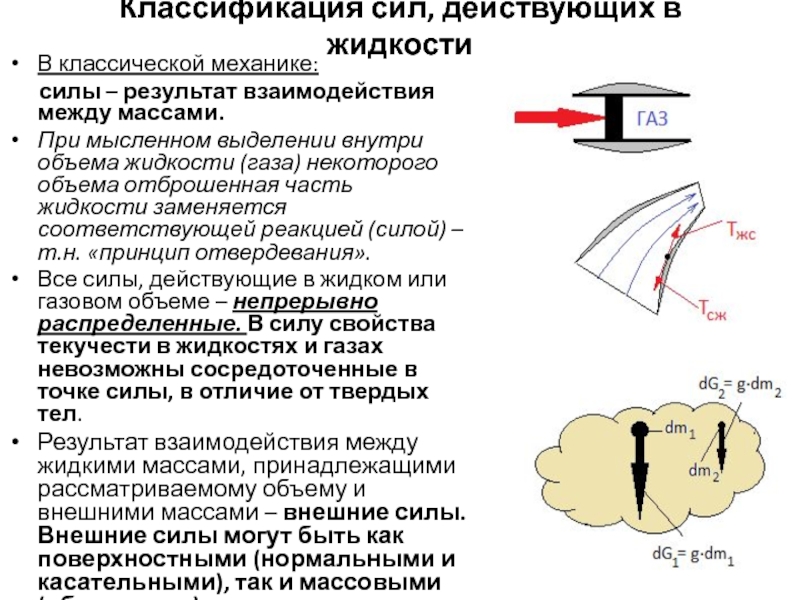
Слайд 17Классификация сил, действующих в жидкости
В классической механике:
силы
При мысленном выделении внутри объема жидкости (газа) некоторого объема отброшенная часть жидкости заменяется соответствующей реакцией (силой) – т.н. «принцип отвердевания».
Все силы, действующие в жидком или газовом объеме – непрерывно распределенные. В силу свойства текучести в жидкостях и газах невозможны сосредоточенные в точке силы, в отличие от твердых тел.
Результат взаимодействия между жидкими массами, принадлежащими рассматриваемому объему и внешними массами – внешние силы. Внешние силы могут быть как поверхностными (нормальными и касательными), так и массовыми (объемными).
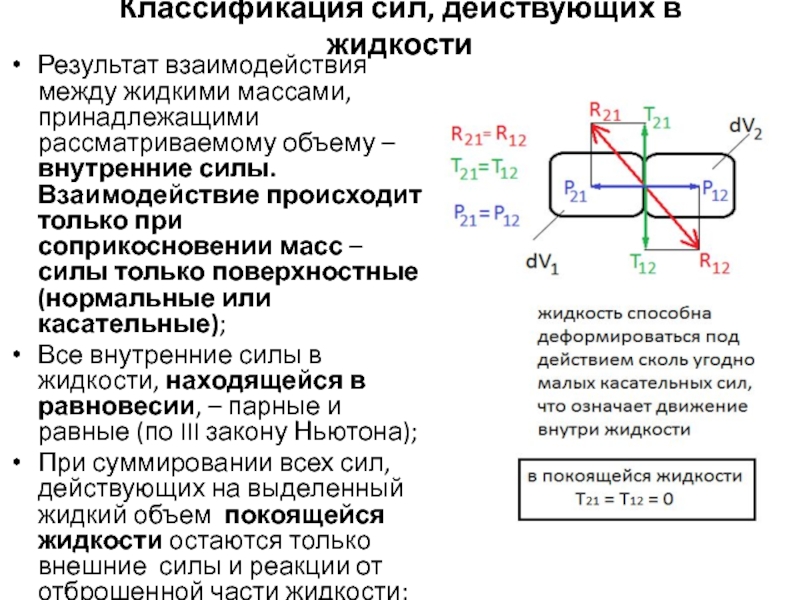
Слайд 18Классификация сил, действующих в жидкости
Результат взаимодействия между жидкими массами, принадлежащими рассматриваемому
Все внутренние силы в жидкости, находящейся в равновесии, – парные и равные (по III закону Ньютона);
При суммировании всех сил, действующих на выделенный жидкий объем покоящейся жидкости остаются только внешние силы и реакции от отброшенной части жидкости;
Слайд 19Силы в покоящейся жидкости
В покоящейся жидкости (τ = 0) силы, возникающие
Среднее гидростатическое давление pср = Pn/F;
Гидростатическое давление в точке p = lim(Pn/F)
при F → 0;
Теорема 1 (Закон Паскаля)
Давление в одной и той же точке покоящейся жидкости одинаково во всех направлениях (во всех сечениях, проведенных через данную точку)
Теорема 2 (для газов)
При отсутствии силы тяжести и других массовых сил давление во всех точках объема газа одинаково






![Параметры, характеризующие жидкую или газообразную среду в данной точкеСкорость - , размерность – [м/с],](/img/tmb/4/376858/eb5c2c4d9b6f2b7e80e00a6abd71adf4-800x.jpg)