Второе начало термодинамики. Энтропия презентация

Энтропия замкнутой (теплоизолированной, внешние силы не совершают работу) макросистемы не уменьшается – она либо возрастает, либо остаётся постоянной.

В замкнутых системах:

Ещё одна формулировка 2-го начала

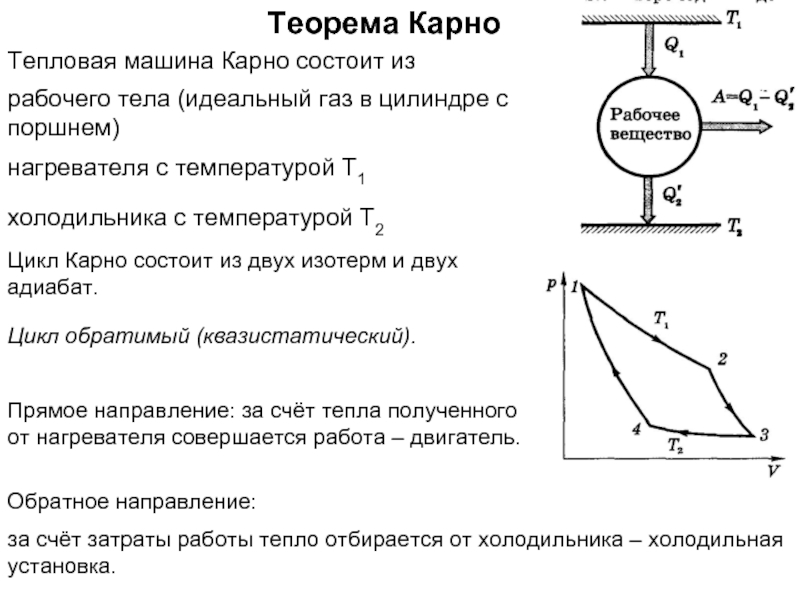
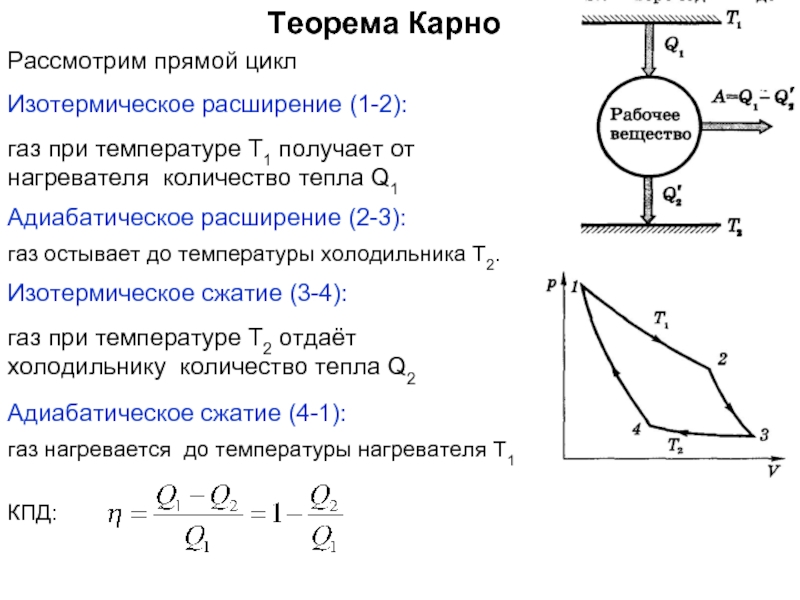
В случае обратимых процессов энтропия замкнутой макросистемы не меняется

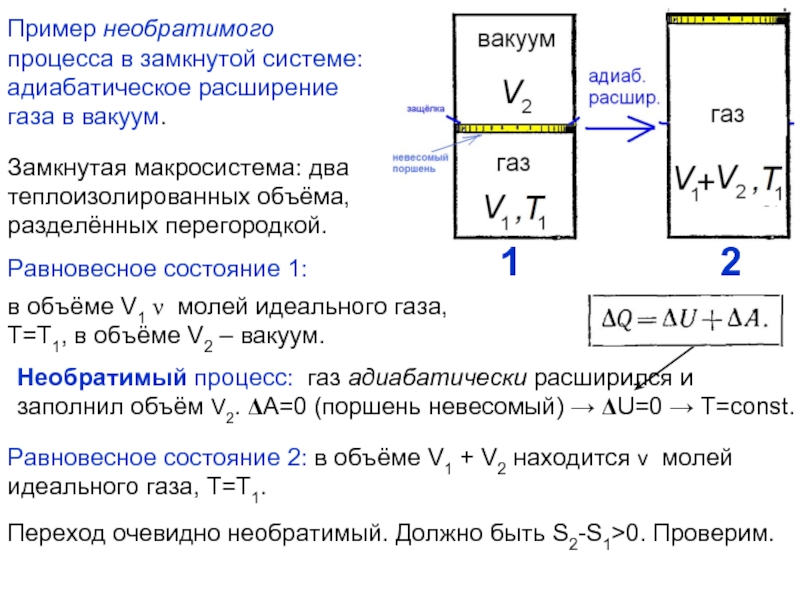
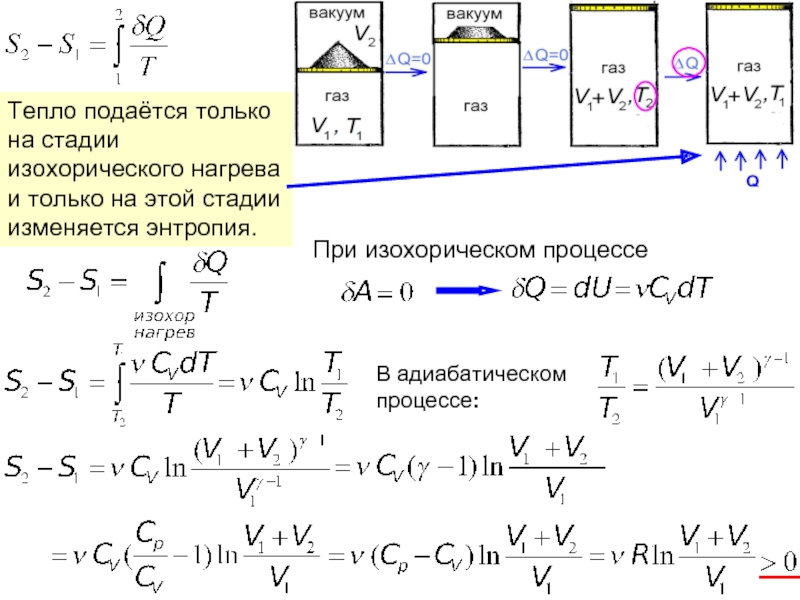
В случае необратимых процессов энтропия замкнутой макросистемы возрастает

Равновесное состояние 1:

в объёме V1 ν молей идеального газа, T=T1, в объёме V2 – вакуум.

Равновесное состояние 2: в объёме V1 + V2 находится ν молей идеального газа, T=T1.

Переход очевидно необратимый. Должно быть S2-S1>0. Проверим.

Газ остынет до температуры Т2 (теперь газ совершил работу за счёт внутренней энергии 0 = ∆U + ∆A).

Изохорически нагреем газ до начальной температуры Т1.

Формула относится только к равновесным процессам.

До сих пор всё происходило в замкнутой (теплоизолированной) системе (∆Q=0).

Теперь в систему подаётся тепло от внешнего нагревателя, она уже незамкнутая.

При изохорическом процессе

Обратный процесс (самопроизвольное сжатие) запрещён вторым началом (поскольку энтропия при этом снижается).

Таким образом, анализ изменения энтропии указывает, какие неравновесные процессы в замкнутой системе возможны (протекают самопроизвольно), а какие нет.

Например, если мысленно разделить объём V, заполненный газом, пополам, то крайне маловероятно, что все молекулы соберутся в одной из его частей, а другая окажется пустой.

И наоборот, если такая ситуация искусственно создана, когда мы убираем перегородку, газ немедленно заполняет весь объём, т.е. система самопроизвольно переходит в более вероятное состояние (и в то же время увеличивается энтропия).

Самопроизвольно макросистема переходит в то состояние, которое наиболее вероятно.

В замкнутых системах:

Самопроизвольные процессы протекают в направлении роста энтропии.

Молекулы газа могут иметь разные импульсы и координаты. Состояние с определёнными значениями всех координат и импульсов всех молекул системы называется микросостоянием.

Любому макросостоянию соответствует громадное число микросостояний.

Чем большим числом способов (микросостояний) может быть осуществлено данное макросостояние, тем оно более вероятно.

Статистический смысл энтропии

Термодинамическая вероятность данного макросостояния W равна числу способов (числу микросостояний), которыми может быть осуществлено данное макросостояние.

Число способов, которым можно разместить в объёме V N молекул пропорционально

Термодинамическая вероятность состояния идеального газа:
W~ VN.

Термодинамическая вероятность W – огромное число (это не математическая вероятность, которая не превосходит 1).

Термодинамическую вероятность называют также статистическим весом.

Статистический смысл энтропии

Связь термодинамической вероятности состояний идеального газа с его объёмом.

Изменение энтропии при расширении газа выражается через термодинамические вероятности состояний.

Более вероятные состояния – менее упорядоченные, более однородные.

Например, самопроизвольные процессы идут в направлении выравнивания давления и температуры.

Принцип возрастания энтропии не относится к открытым системам, например, живым.

Гипотеза о «тепловой смерти вселенной».

система обладает наименьшей возможной энергией,

её внутренняя энергия распределена между составляющими ее частицами единственным способом, а именно

все электроны в атомах находятся при этом в наинизших энергетических состояниях,

а атомы располагаются в пространстве определенным образом (в узлах кристаллической решетки твердого тела).

Благодаря полной упорядоченности этого единственного состояния его термодинамическая вероятность W = 1.

Нернст 1906, Планк 1911

Возможность определять абсолютное значения энтропии.

Для обратимых процессов

Энтропия идеального газа

Найдём S2 – S1 для двух состояний ν молей идеального газа: V1, T1 и V2, T2

Адиабатическое расширение в вакуум

В замкнутой системе мы хотим отнять тепло ΔQ1 от нагретого тела и за счёт этого тепла совершить работу.

Энтропия этого тела уменьшится на величину :

Но энтропия замкнутой системы не может убывать.

Тепло, переданное второму телу, ∆Q2 меньше, чем ∆Q1 (иначе не получить работу).

Поэтому должно быть другое тело, энтропия которого возрастёт настолько же или больше.

Таким образом этому телу должно быть передано тепло ∆Q2 и при этом должно быть ∆S2≥ ∆S1, т.е.

обратимо отнять тепло ΔQ1 от нагревателя,

обратимо отдать часть тепла ΔQ2 холодильнику,

разность ΔQ1 — ΔQ2 передать поршню в виде механической работы ΔА.

холодильника с температурой Т2

Цикл Карно состоит из двух изотерм и двух адиабат.

Цикл обратимый (квазистатический).

Прямое направление: за счёт тепла полученного от нагревателя совершается работа – двигатель.

Обратное направление:
за счёт затраты работы тепло отбирается от холодильника – холодильная установка.

газ остывает до температуры холодильника Т2.

газ при температуре Т2 отдаёт холодильнику количество тепла Q2

Рассмотрим прямой цикл

Адиабатическое сжатие (4-1):

газ нагревается до температуры нагревателя Т1

КПД:

Теорема Карно:

КПД обратимых двигателей, работающих по циклу Карно, зависит только от температур Т1 и Т2 – нагревателя и холодильника, но не зависит ни от устройства двигателя, ни от вида рабочего вещества.

КПД любой необратимой (реальной) тепловой машины, работающей с тем же нагревателем и холодильником, всегда ниже, чем у машины работающей по обратимому циклу Карно:

Проблема энергосбережения при использовании углеводородного топлива наиболее эффективно решается на основе прямого преобразования химической энергии органического топлива в электрическую энергию с помощью водородных топливных элементов

Не требует источника электричества для зарядки.

Напряжение 13.9 В, мощность 19.4 Вт.

Плотность энергии: 882 Вт/л - рекордная!

Размеры: 65*18*19 мм3 = 22 мл.

7

Разработка японской фирмы Casio: источник питания для ноутбука

ООО инновационная компания «МЕВОДЕНА», резидент СКОЛКОВО (к. 103)

Мембранная панель разработанная в ГУТ обращена непосредственно в плазму.

Large Helical Device

14