тела
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Вращательное движение твердого тела. Уравнение вращательного движения. Угловая скорость и угловое ускорение тела презентация
Содержание
- 1. Вращательное движение твердого тела. Уравнение вращательного движения. Угловая скорость и угловое ускорение тела
- 2. Вращательным движением твердого тела называется такое его
- 3. Все остальные точки тела движутся в плоскостях,
- 4. Зададим направление оси вращения z. Проведем через
- 5. Двугранный угол между этими полуплоскостями,
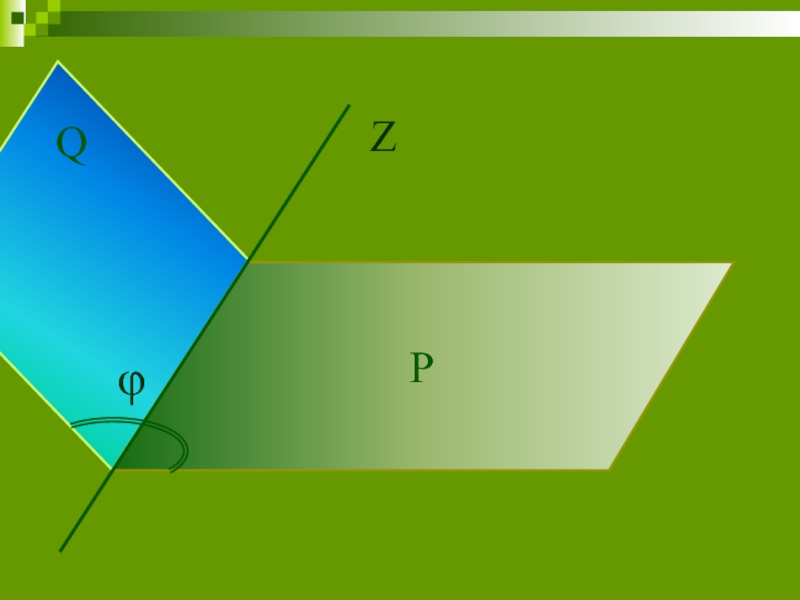
- 6. P Q φ Z
- 7. При вращении тела угол поворота
- 8. Величина, характеризующая быстроту изменения угла поворота
- 9. Числовая величина, характеризующая быстроту изменения угловой скорости
- 10. Пусть в начальный момент времени t0=0 угол
- 11. Проинтегрируем уравнение в пределах, соответствующих начальному моменту t0=0 и произвольному моменту времени t:
- 12. Уравнение равнопеременного движения тела Вращение тела,
- 13. При этом, если абсолютная величина угловой скорости
- 14. Из формулы угловой скорости находим
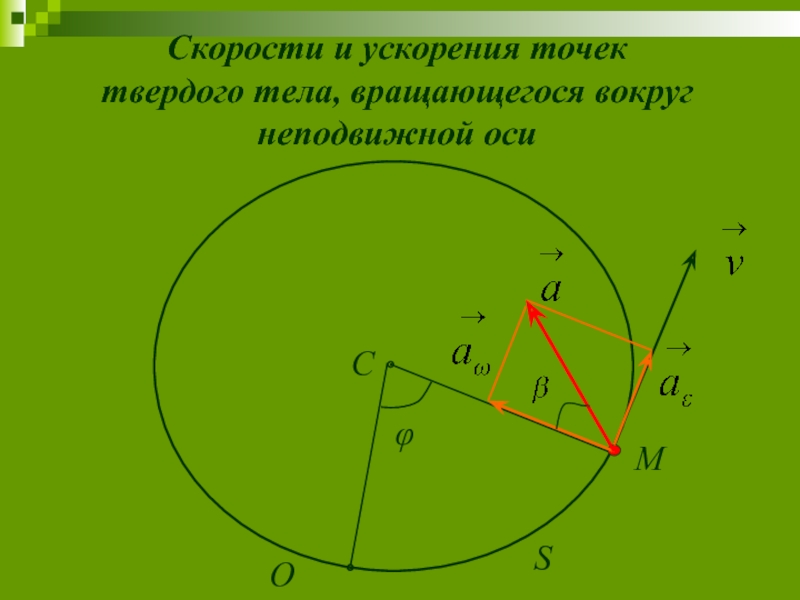
- 15. φ O S M
- 16. Определим модуль скорости точки М, называемой вращательной
- 17. Определим ускорения точек вращающегося тела: Модуль вращательного
- 18. Модуль центростремительного ускорения точки твердого тела равен
- 19. Модуль полного ускорения точки равен
- 20. Тангенс угла , составленного вектором ускорения с радиусом окружности СМ:
- 21. Пример решения задачи
- 22. Пример 1 Вращение маховика в период пуска
- 23. Определить модуль и направление ускорения точки, отстоящей
- 24. M O
- 25. Решение: По уравнению вращения маховика находим
- 26. Используя формулу
- 27. Далее вычисляем:
- 28. Направление ускорения точки определяется углом :
- 29. Пример 2 Якорь электродвигателя, имеющий частоту вращения
- 30. Дано: n=50c-1 N=500 ε=?
- 31. Решение: Закон движения:
- 32. С другой стороны: Так как якорь остановился,
- 33. Отсюда
Вращательным движением твердого тела называется такое его движение, при котором все точки, принадлежащие некоторой прямой, неизменно связанной с телом, остаются неподвижными.
Эта прямая называется осью вращения тела.
Слайд 1Вращательное движение твердого тела
Уравнение вращательного движения
Угловая скорость и угловое ускорение
Слайд 2Вращательным движением твердого тела называется такое его движение, при котором все
точки, принадлежащие некоторой прямой, неизменно связанной с телом, остаются неподвижными.
Эта прямая называется осью вращения тела.
Слайд 3Все остальные точки тела движутся в плоскостях, перпендикулярных оси вращения, и
описывают окружности, центры которых лежат на этой оси.
Слайд 4 Зададим направление оси вращения z. Проведем через эту ось две полуплоскости:
неподвижную полуплоскость P и подвижную полуплоскость Q, связанную с твердым телом и вращающуюся вместе с ним.
Слайд 5Двугранный угол между этими полуплоскостями, отчитываемый от неподвижной полуплоскости
P к подвижной полуплоскости Q, называется углом поворота тела.
Слайд 7 При вращении тела угол поворота изменяется в зависимости от
времени, т.е. является функцией времени t:
Это уравнение называется уравнением вращательного движения тела.
Оно полностью определяет положение тела в любой момент времени.
Слайд 8 Величина, характеризующая быстроту изменения угла поворота с течением времени,
называется угловой скоростью тела (1 рад/с).
Угловая скорость
и угловое ускорение тела
Слайд 9Числовая величина, характеризующая быстроту изменения угловой скорости с течением времени, называется
угловым ускорением тела
(1 рад/c2).
(1 рад/c2).
Слайд 10 Пусть в начальный момент времени t0=0 угол поворота имеет значение
, тогда
Уравнение равномерного вращения тела
Вращение тела с постоянной скоростью называется равномерным.
Слайд 11 Проинтегрируем уравнение в пределах, соответствующих начальному моменту t0=0 и произвольному моменту
времени t:
Слайд 12Уравнение равнопеременного
движения тела
Вращение тела, при котором угловое ускорение постоянно, называют
равнопеременным вращением.
Слайд 13При этом, если абсолютная величина угловой скорости увеличивается, то вращение называют
равноускоренным, а если уменьшается – равнозамедленным.
Слайд 14Из формулы угловой скорости находим т.е. при равнопеременном вращении абсолютное значение углового
ускорения тела равно отношению изменения угловой скорости тела за некоторый промежуток времени к числовой величине этого промежутка.
Слайд 16 Определим модуль скорости точки М, называемой вращательной или окружной скоростью этой
точки
Модуль вращательной скорости точки твердого тела равен произведению расстояния от точки до оси вращения на угловую скорость тела.
Модули вращательных скоростей различных точек вращающегося тела пропор-циональны расстояниям от этих точек до оси вращения.
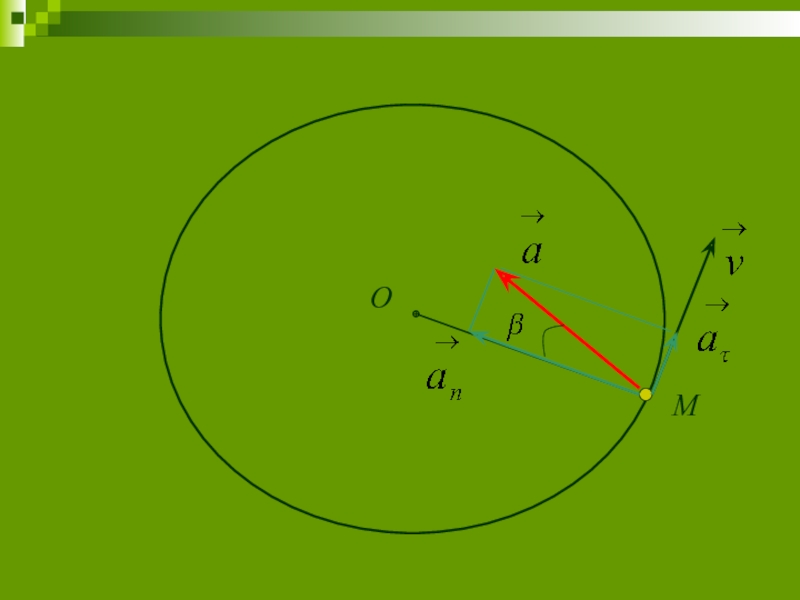
Слайд 17Определим ускорения точек вращающегося тела:
Модуль вращательного ускорения точки твердого тела равен
произведению расстояния от точки до оси вращения на модуль углового ускорения точки.
Слайд 18Модуль центростремительного ускорения точки твердого тела равен произведению расстояния от точки
до оси вращения на квадрат угловой скорости точки.
Слайд 22Пример 1
Вращение маховика в период пуска машины определяется уравнением
где t –
в секундах, – в радианах.
Слайд 23Определить модуль и направление ускорения точки, отстоящей от оси вращения на
расстоянии 50 см, в тот момент, когда ее скорость равна 8 м/с.
Слайд 26Используя формулу
, находим момент времени t1, когда скорость точки М равна 8 м/с:
Из (1) находим t1:
Слайд 29Пример 2
Якорь электродвигателя, имеющий частоту вращения n=50c-1, после выключения тока, сделав
N=500 оборотов, остановился. Определить угловое ускорение якоря.
