- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Волновые процессы. (Тема 28) презентация
Содержание
- 1. Волновые процессы. (Тема 28)
- 2. 1. ВИДЫ ВОЛН Волнами называется процесс распространения
- 3. 2. ПОПЕРЕЧНЫЕ И ПРОДОЛЬНЫЕ ВОЛНЫ В
- 4. 3. ВОЛНОВОЙ ФРОНТ. ВОЛНОВАЯ ПОВЕРХНОСТЬ Распространяясь от
- 5. 4. ВОЛНЫ ПЛОССКАЯ И СФЕРИЧЕСКАЯ Волновые поверхности
- 6. 5. ДЛИНА ВОЛНЫ На рисунке показано смещение
- 7. 6. УРАВНЕНИЕ ПЛОССКОЙ ВОЛНЫ (I) Уравнением
- 8. 6. УРАВНЕНИЕ ПЛОССКОЙ ВОЛНЫ (II) Для
- 9. 7. УРАВНЕНИЕ СФЕРИЧЕСКОЙ ВОЛНЫ Всякий реальный источник
- 10. 8. ВОЛНОВОЕ УРАВНЕНИЕ Уравнение любой волны
- 11. 9. СКОРОСТЬ УПРУГИХВОЛН Сравнивая полученное
- 12. 10. ЭНЕРГИЯ УПРУГОЙ ВОЛНЫ Пусть в
- 13. 11. ПОТОК И ПЛОТНОСТЬ ПОТОКА ЭНЕРГИИ ВОЛНЫ
- 14. 12. ИНТЕНСИВНОСТЬ ВОЛНЫ Плотность потока энергии как
- 15. 13. СТОЯЧИЕ ВОЛНЫ Колебания, возникающие при наложении
- 16. 14. КОЛЕБАНИЯ СТРУНЫ В закрепленной с двух
- 17. 15. ЗВУК Упругие волны в воздухе,
- 18. 16. ГРОМКОСТЬ ЗВУКА Уровень громкости звука определяется
- 19. §2. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
- 20. 1. УРАВНЕНИЯ МАКСВЕЛЛА Запишем уравнения Максвелла в
- 21. 2. ВОЛНОВОЕ УРАВНЕНИЕ Для однородной нейтральной непроводящей
- 22. 3. СКОРОСТЬ ЭМВ Для однородной нейтральной непроводящей
- 23. 4. УРАВНЕНИЯ МАКСВЕЛЛА ДЛЯ ПЛОСКОЙ ЭМВ (I)
- 24. 4. УРАВНЕНИЯ МАКСВЕЛЛА ДЛЯ ПЛОСКОЙ ЭМВ (II)
- 25. 4. УРАВНЕНИЯ МАКСВЕЛЛА ДЛЯ ПЛОСКОЙ ЭМВ (III)
- 26. 4. УРАВНЕНИЯ МАКСВЕЛЛА ДЛЯ ПЛОСКОЙ ЭМВ (IV)
- 27. 5. ПЛОСКАЯ ЭМВ (I) Возьмем для описания
- 28. 5. ПЛОСКАЯ ЭМВ(II) Решения волновых уравнений должны
- 29. 5. ПЛОСКАЯ ЭМВ(III) Решения волновых уравнений должны
- 30. 6. ЭНЕРГИЯ ЭМВ Электромагнитные волны переносят энергию.
- 31. 7. ЭМВ В ПРИРОДЕ И ТЕХНИКЕ
Слайд 21. ВИДЫ ВОЛН
Волнами называется процесс
распространения колебаний
в пространстве с течением
времени.
Характерное свойство
состоит в том, что перенос
энергии волной происходит
без переноса вещества.
Основными видами волн являются механические (упругие ) волны:
в частности звуковые и сейсмические волны, волны на поверхности воды;
и электромагнитные волны:
в частности световые волны и радиоволны.
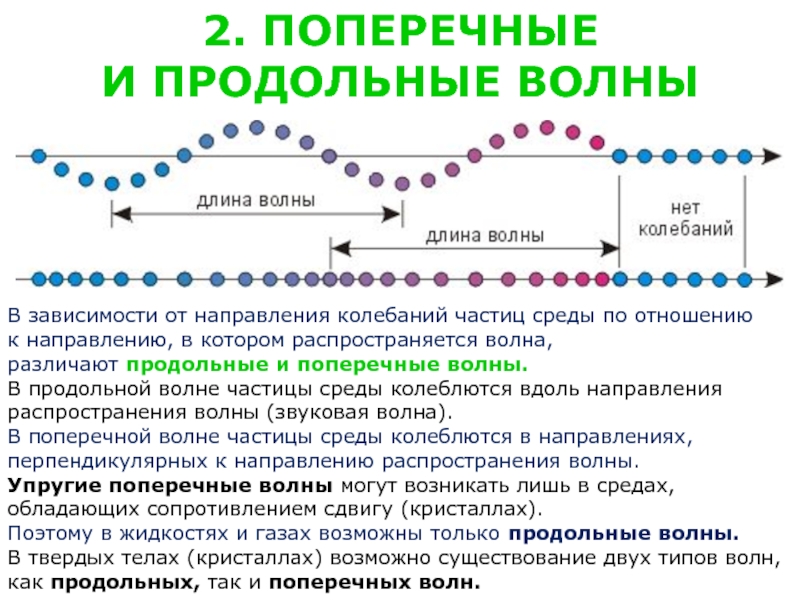
Слайд 32. ПОПЕРЕЧНЫЕ
И ПРОДОЛЬНЫЕ ВОЛНЫ
В зависимости от направления колебаний частиц среды
к направлению, в котором распространяется волна,
различают продольные и поперечные волны.
В продольной волне частицы среды колеблются вдоль направления
распространения волны (звуковая волна).
В поперечной волне частицы среды колеблются в направлениях,
перпендикулярных к направлению распространения волны.
Упругие поперечные волны могут возникать лишь в средах, обладающих сопротивлением сдвигу (кристаллах).
Поэтому в жидкостях и газах возможны только продольные волны.
В твердых телах (кристаллах) возможно существование двух типов волн, как продольных, так и поперечных волн.
Слайд 43. ВОЛНОВОЙ ФРОНТ.
ВОЛНОВАЯ ПОВЕРХНОСТЬ
Распространяясь от источника колебаний, волновой процесс охватывает все
Геометрическое место точек, до которых доходят колебания к данному моменту времени, называется фронтом волны
или волновым фронтом.
Фронт волны отделяет часть пространства, уже вовлеченную в волновой процесс,
от области, в которой колебания еще не возникли.
Геометрическое место точек,
колеблющихся в одинаковой фазе,
называется волновой поверхностью.
Волновую поверхность можно провести через
любую точку пространства,
охваченного волновым процессом.
Волновых поверхностей бесконечно много.
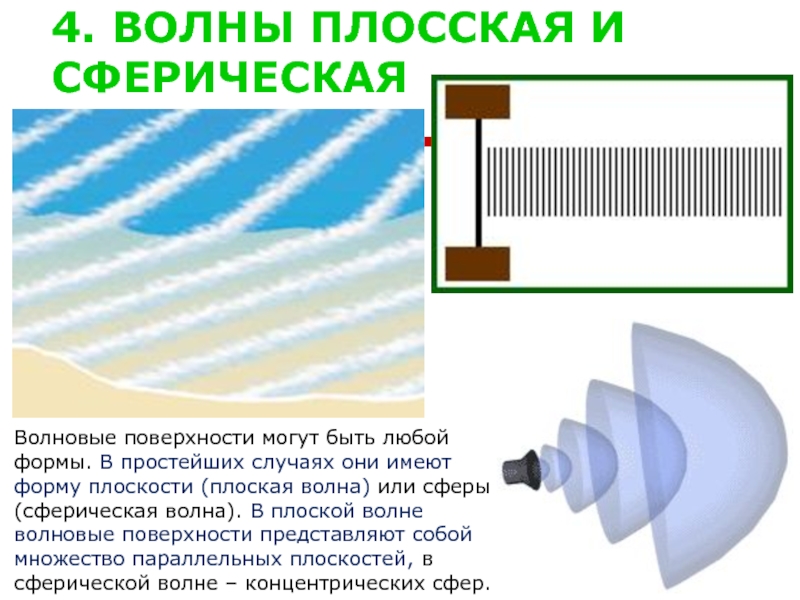
Слайд 54. ВОЛНЫ ПЛОССКАЯ И СФЕРИЧЕСКАЯ
Волновые поверхности могут быть любой
формы. В простейших
форму плоскости (плоская волна) или сферы
(сферическая волна). В плоской волне
волновые поверхности представляют собой
множество параллельных плоскостей, в
сферической волне – концентрических сфер.
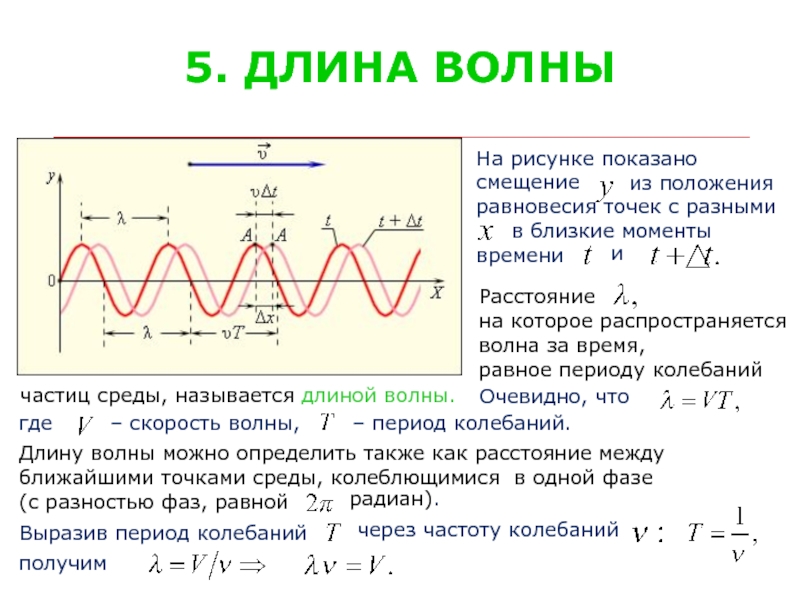
Слайд 65. ДЛИНА ВОЛНЫ
На рисунке показано
смещение
равновесия точек с разными
в
времени
Расстояние
на которое распространяется
волна за время,
равное периоду колебаний
частиц среды, называется длиной волны.
где
Длину волны можно определить также как расстояние между
ближайшими точками среды, колеблющимися в одной фазе
(с разностью фаз, равной
Выразив период колебаний
получим
из положения
и
Очевидно, что
– период колебаний.
– скорость волны,
радиан).
через частоту колебаний
Слайд 76. УРАВНЕНИЕ
ПЛОССКОЙ ВОЛНЫ (I)
Уравнением волны называется выражение,
которое определяет смещение
частицы от её равновесного положения
как функцию его координат и времени:
Эта функция периодическая относительно времени
и относительно пространственных координат
Упростим ситуацию, направив ось
по направлению
распространения волны.
Тогда плоские волновые поверхности будут
перпендикулярными оси
Поскольку все точки
волновой поверхности колеблются одинаково,
то смещение
будет зависеть только от
и
Колебания точек, лежащих в плоскости
имеют вид
Найдём вид
колебаний в плоскости с произвольным значением
Слайд 86. УРАВНЕНИЕ
ПЛОССКОЙ ВОЛНЫ (II)
Для того, чтобы пройти путь от начала
до плоскости с координатой
требуется время
– скорость распространения волны.
Следовательно, колебания частиц в плоскости
будут отставать по времени на
от колебаний
частиц, лежащих в плоскости
то есть
Аргумент гармонической функции – это фаза волны:
– волновое число (модуль волнового вектора).
При произвольной ориентации осей
Слайд 97. УРАВНЕНИЕ СФЕРИЧЕСКОЙ ВОЛНЫ
Всякий реальный источник волн обладает
некоторой протяженностью (размером).
будут совершать колебания с запаздыванием по времени на
Даже если волна не поглощается средой, ее амплитуда уменьшается
с удалением от источника по закону
по поверхности все большего радиуса.
– амплитуда на единичном радиусе.
Однако если ограничиться рассмотрением волны на расстояниях от источника значительно превышающих его размеры,
то источник можно считать точечным.
В изотропной и однородной средах волна,
от точечного источника будет сферической.
Допустим, что фаза колебаний источника имеет вид
Тогда точки среды, лежащие на волновой поверхности радиуса
Тогда
т.к. энергия распределяется
Слайд 108. ВОЛНОВОЕ
УРАВНЕНИЕ
Уравнение любой волны является решением
уравнения, называемого волновым.
Чтобы установить
Сложим производные по координатам:
описывающей плоскую волну:
Слайд 119. СКОРОСТЬ
УПРУГИХВОЛН
Сравнивая полученное уравнение движения
с одномерным волновым уравнением
скорость
из отношения модуля Юнга среды к ее плотности:
Пусть в направлении оси
распространяется
продольная плоская волна.
цилиндрический объём с площадью
Выделим в среде
и длиной
Составим для этого объёма уравнение движения:
– относительная деформация цилиндра,
– модуль упругости среды (модуль Юнга).
Таким образом,
приходим к
выводу, что
Слайд 1210. ЭНЕРГИЯ УПРУГОЙ ВОЛНЫ
Пусть в однородной среде вдоль оси
распространяется
Выделим в среде элементарный объем
Сумма кинетической и потенциальной энергии упругой деформации выделенного объема дает его полную механическую энергию, то есть
Слайд 1311. ПОТОК И ПЛОТНОСТЬ ПОТОКА ЭНЕРГИИ ВОЛНЫ
Среда, в которой распространяется волна,
различные точки среды самой волной;
Количество энергии, переносимое волной через некоторую
поверхность в единицу времени, называется потоком энергии:
Эта энергия доставляется от источника колебаний в
волна переносит с собой энергию.
Для характеристики течения энергии в разных точках введена
векторная физическая величина – плотность потока энергии:
Зная плотность потока энергии во всех
точках произвольной поверхности
можно вычислить поток энергии через эту поверхность:
Слайд 1412. ИНТЕНСИВНОСТЬ ВОЛНЫ
Плотность потока энергии как и объемная плотность энергии различна
в разных точках пространства (меняется амплитуда и плотность среды),
а в данной точке изменяется со временем по закону квадрата синуса.
Среднее значение квадрата синуса за период равно
среднего по времени значение плотности потока энергии справедливо
Эта величина называется интенсивностью волны
Интенсивность волны в данной точке это среднее по времени значение
плотности потока энергии волны в этой точке пространства.
Полученные выражения для интенсивности и объемной плотности энергии
справедливы для всех механических волн.
поэтому для
Слайд 1513. СТОЯЧИЕ ВОЛНЫ
Колебания, возникающие при наложении двух плоских встречных
волн с одинаковой
В каждой точке стоячей волны происходят колебания той же частоты, что у встречных бегущих волн.
Выбирая подходящим образом начало отсчёта
и
получим:
Амплитуда колебаний
периодически меняется
В точках, для которых:
амплитуда максимальна – это пучности;
минимальна – узлы.
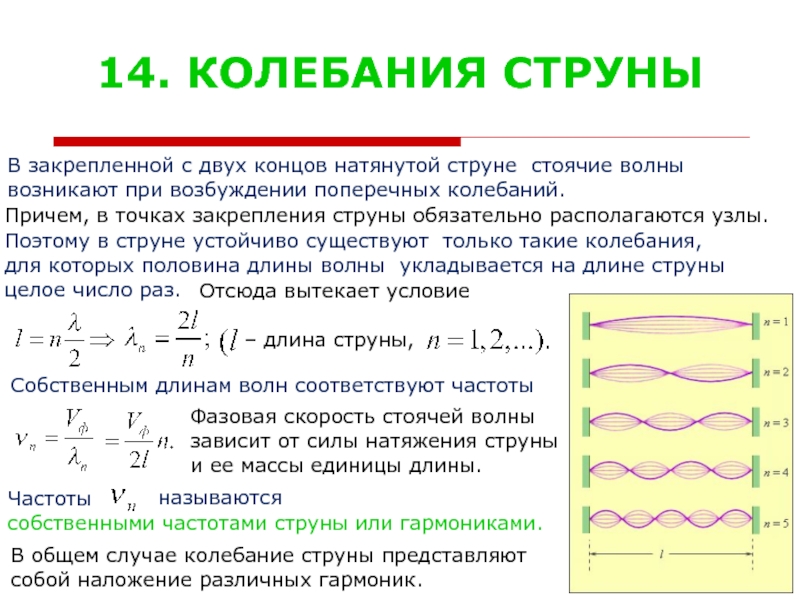
Слайд 1614. КОЛЕБАНИЯ СТРУНЫ
В закрепленной с двух концов натянутой струне стоячие волны
Причем, в точках закрепления струны обязательно располагаются узлы.
Поэтому в струне устойчиво существуют только такие колебания,
для которых половина длины волны укладывается на длине струны целое число раз.
Отсюда вытекает условие
– длина струны,
Собственным длинам волн соответствуют частоты
Фазовая скорость стоячей волны зависит от силы натяжения струны и ее массы единицы длины.
Частоты
собственными частотами струны или гармониками.
называются
В общем случае колебание струны представляют
собой наложение различных гармоник.
Слайд 1715. ЗВУК
Упругие волны в воздухе, имеющие частоту в
пределах от 16 Гц
человека ощущение звука.
Поэтому упругие волны в любой среде,
имеющие частоту в этом диапазоне, называют
звуковыми волнами или просто звуком.
Упругие волны с частотами,
меньшими чем 16 Гц,
называют инфразвуком.
Упругие волны с частотами
больше чем 20 кГц,
называют ультразвуком.
Воспринимаемые звуки люди
различают по высоте (частоте),
тембру (акустическому спектру)
и громкости (интенсивности волны).
Слайд 1816. ГРОМКОСТЬ ЗВУКА
Уровень громкости звука определяется как десятичный логарифм отношения интенсивности
к интенсивности на пороге слышимости:
Принято, что для человека
На практике принято использоваться в 10 раз меньшими
единицами уровня громкости звука – децибелами (дб):
Весь диапазон интенсивностей, при
которых волна вызывает в ухе человека
звуковое ощущение, соответствует
уровню громкости от 0 до 130 дб.
Отношение
интенсивностей
двух волн:
Слайд 201. УРАВНЕНИЯ МАКСВЕЛЛА
Запишем уравнения Максвелла в дифференциальной форме:
В случае однородной
Сделаем замену для
и
с помощью материальных уравнений:
нейтральной
непроводящей
среды уравнения примут вид:
Переменное магнитное поле порождает электрическое и наоборот.
Значит последовательность взаимных превращений электрического
и магнитного полей может представлять собой волну.
Убедимся в этом.
Слайд 212. ВОЛНОВОЕ УРАВНЕНИЕ
Для однородной нейтральной непроводящей среды система уравнений
Максвелла имеет вид
Возьмем
Воспользуемся выражением для ротора из уравнения (3):
Раскроем двойное векторное произведение с учетом уравнения (4):
Слайд 223. СКОРОСТЬ ЭМВ
Для однородной нейтральной непроводящей среды получено волновое
уравнение
Электрическая и
со скоростью света в вакууме
С учётом этого волновые уравнения для напряженности электрического
и напряженности магнитного полей принимают вид:
Полученные волновые уравнения неразрывно связаны между собой,
так как они получены из уравнений Максвелла, которые одновременно
содержат напряженности и электрического и магнитного полей.
Из этих волновых уравнений следует, что электромагнитные поля могут
существовать в виде электромагнитных волн,
фазовая скорость которых зависит от свойств среды
Слайд 234. УРАВНЕНИЯ МАКСВЕЛЛА
ДЛЯ ПЛОСКОЙ ЭМВ (I)
Перепишем уравнения Максвелла для однородной нейтральной
непроводящей
в координатной форме:
Направим ось x перпендикулярно волновым поверхностям плоской ЭМВ.
Тогда векторы
не будут зависеть от координат y и z. То есть
а значит, и их проекции на координатные оси
и
и
Слайд 244. УРАВНЕНИЯ МАКСВЕЛЛА
ДЛЯ ПЛОСКОЙ ЭМВ (II)
Упростим систему уравнения Максвелла для однородной
диэлектрической (непроводящей) среды
для случая плоской волны, распространяющей вдоль оси x.
пропадает зависимость всех компонент поля от поперечных координат
y и z.
При этом
Поэтому система уравнений упрощается к виду:
Слайд 254. УРАВНЕНИЯ МАКСВЕЛЛА
ДЛЯ ПЛОСКОЙ ЭМВ (III)
Выпишем в координатной форме систему уравнений
плоской волны, распространяющейся вдоль оси x в однородной
нейтральной диэлектрической (непроводящей) среде
Уравнение (4) и первое из уравнений (3) показывают, что
зависеть ни от x, ни от t.
такой же результат для
могут быть обусловлены лишь постоянными однородными полями,
накладывающимися на электромагнитные волны.
имеет составляющих вдоль оси x.
перпендикулярны к направлению распространения волны,
то есть электромагнитные волны в однородном диэлектрике поперечны.
не может
Уравнение (2) и первое из уравнений (1) дают
и
Следовательно, отличные от нуля
Само поле волны не
и
Отсюда вытекает, что векторы
Слайд 264. УРАВНЕНИЯ МАКСВЕЛЛА
ДЛЯ ПЛОСКОЙ ЭМВ (IV)
Предполагая отсутствие постоянных (стационарных) полей
запишем
распространяющейся вдоль оси x однородной нейтральной непроводящей
(диэлектрической) среды:
Можно заметить, что оставшиеся 4 уравнения объединяются в две
независимые группы:
Первая группа уравнений связывает компоненты
а вторая – компоненты
Если в пространстве было создано переменное электрическое поле
то оно будет порождать переменное магнитное поле
которое в свою очередь создаст переменное электрическое поле
Поля
и
и
при этом не возникают.
и
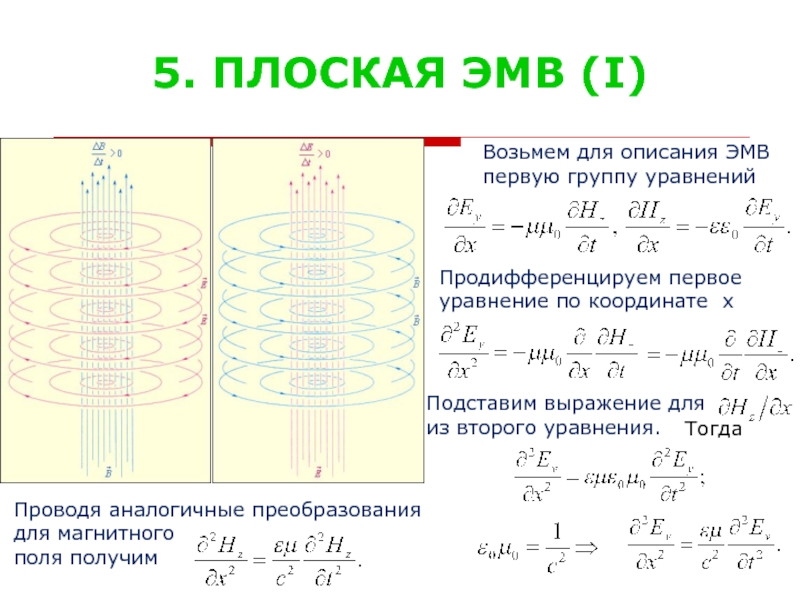
Слайд 275. ПЛОСКАЯ ЭМВ (I)
Возьмем для описания ЭМВ
первую группу уравнений
Продифференцируем первое
уравнение
Подставим выражение для
из второго уравнения.
Проводя аналогичные преобразования
для магнитного
поля получим
Тогда
Слайд 285. ПЛОСКАЯ ЭМВ(II)
Решения волновых уравнений должны
удовлетворять и уравнениям Максвелла
Это
и в каждой точке пространства колебания полей
происходить в одной фазе.
Это означает, что колебания полей происходят с одинаковой частотой и начальной фазой; эти колебания распространяются с одинаковой
будут
и
Это возможно, если
скоростью (длиной волны).
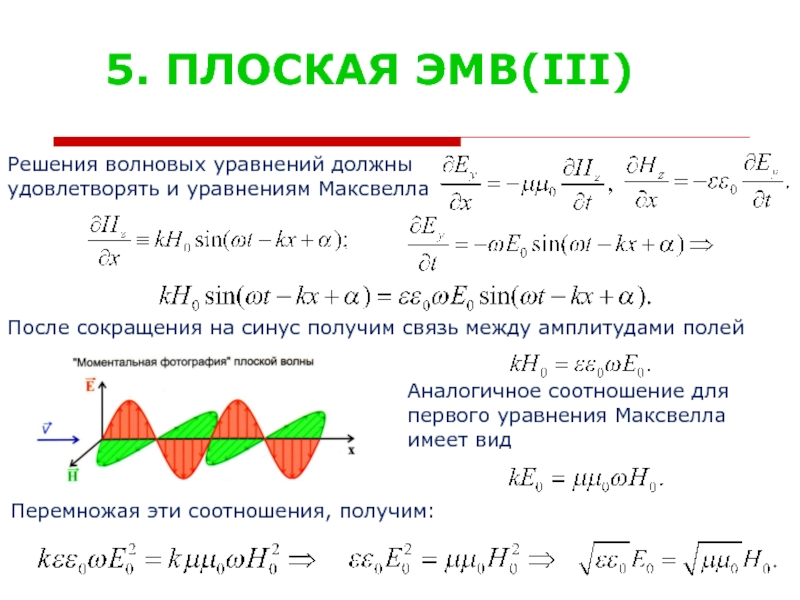
Слайд 295. ПЛОСКАЯ ЭМВ(III)
Решения волновых уравнений должны
удовлетворять и уравнениям Максвелла
После
Аналогичное соотношение для
первого уравнения Максвелла
имеет вид
Перемножая эти соотношения, получим:
Слайд 306. ЭНЕРГИЯ ЭМВ
Электромагнитные волны переносят энергию.
Плотность потока энергии волны можно
объемную плотность энергии волны на её фазовую скорость:
Плотность энергии ЭМВ слагается из плотности
энергии электрического и магнитного полей:
В векторном виде
Вектор плотности потока энергии ЭМВ
называется вектором Пойнтинга.
Среднее по времени значение модуля
вектора Пойнтинга – это интенсивность волны: