12
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Уравнения Лагранжа ii рода. Обобщённые координаты, скорости и силы презентация
Содержание
- 1. Уравнения Лагранжа ii рода. Обобщённые координаты, скорости и силы
- 2. Определять положение любой точки механической системы Научиться
- 3. Обобщенные координаты Обобщенные координаты – это независимые
- 4. ПОНЯТИЕ СТЕПЕНИ СВОБОДЫ Число независимых между собой
- 5. В несвободной механической системе
- 6. 6 КОЛИЧЕСТВО СТЕПЕНЕЙ СВОБОДЫ Обобщенные координаты У
- 7. ОПРЕДЕЛЕНИЕ ПОЛОЖЕНИЯ ТОЧЕК МС Тогда радиус-векторы всех
- 8. ОБОБЩЁННЫЕ СКОРОСТИ Обобщенные скорости При движении системы
- 9. ОБОБЩЁННЫЕ СИЛЫ Обобщенные силы Рассмотрим МС, состоящую
- 10. ОБОБЩЁННЫЕ СИЛЫ Обобщенные силы Поскольку изменяется только
- 11. ОБОБЩЁННЫЕ СИЛЫ Обобщенные силы - обобщённая сила, соответствующая координате
- 12. 12 Обобщённые силы – это величины, равные
- 13. 13 Обобщенные силы ПРИМЕР (ДВОЙНОЙ МАЯТНИК)
- 14. 13 Обобщенные силы ПРИМЕР (ДВОЙНОЙ МАЯТНИК)
- 15. 14 Обобщенные силы
Определять положение любой точки механической системы Научиться описывать движение механической системы с несколькими степенями свободы Цель введения обобщенных координат, скоростей и сил 2
Слайд 1УРАВНЕНИЯ ЛАГРАНЖА II РОДА.
ОБОБЩЁННЫЕ КООРДИНАТЫ,
СКОРОСТИ И СИЛЫ.
ЛЕКЦИИ ПО ТЕОРЕТИЧЕСКОЙ МЕХАНИКЕ.
Динамика
ЛЕКЦИЯ
Слайд 2Определять положение любой точки механической системы
Научиться описывать движение механической системы с
несколькими степенями свободы
Цель введения обобщенных координат, скоростей и сил
2
Слайд 3Обобщенные координаты
Обобщенные координаты – это независимые между собой параметры любой размерности,
однозначно определяющие положение механической системы в пространстве.
3
ОБОБЩЕННЫЕ КООРДИНАТЫ
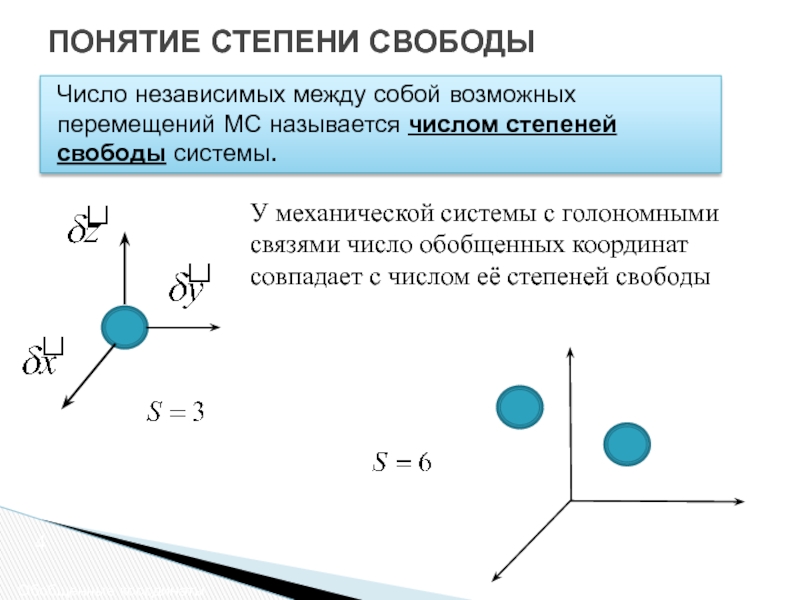
Слайд 4ПОНЯТИЕ СТЕПЕНИ СВОБОДЫ
Число независимых между собой возможных перемещений МС называется числом
степеней свободы системы.
4
У механической системы с голономными связями число обобщенных координат совпадает с числом её степеней свободы
Обобщенные координаты
Слайд 5В несвободной механической системе декартовых координат ее точек
должны удовлетворять уравнениям связей, поэтому независимыми среди них будут только координат.
5
Если бы система была свободной, то все декартовых координат ее точек были бы независимыми.
КОЛИЧЕСТВО СТЕПЕНЕЙ СВОБОДЫ
Обобщенные координаты
1
2
Слайд 66
КОЛИЧЕСТВО СТЕПЕНЕЙ СВОБОДЫ
Обобщенные координаты
У свободного твёрдого тела 6 степеней свободы:
3 поступательных
вдоль осей координат и 3 вращательных вокруг этих осей.
Слайд 7ОПРЕДЕЛЕНИЕ ПОЛОЖЕНИЯ ТОЧЕК МС
Тогда радиус-векторы всех точек системы можно определить как
функцию обобщенных координат
Обобщенные координаты будем обозначать буквой -
7
Обобщенные координаты
Слайд 8ОБОБЩЁННЫЕ СКОРОСТИ
Обобщенные скорости
При движении системы её обобщённые координаты будут меняться со
временем по закону
- кинематическое уравнение движения в обобщённых координатах.
Размерность обобщённой скорости зависит от размерности соответствующей обобщённой координаты.
- кинематическое уравнение движения в обобщённых координатах.
Размерность обобщённой скорости зависит от размерности соответствующей обобщённой координаты.
Производные от обобщённых координат по времени называются обобщёнными скоростями
Слайд 9ОБОБЩЁННЫЕ СИЛЫ
Обобщенные силы
Рассмотрим МС, состоящую из n материальных точек, на которые
действуют силы
Пусть система имеет S степеней свободы и ее положение определяется обобщенными координатами
Сообщим системе такое независимое возможное перемещение, при котором координата получает приращение а остальные координаты не изменяются.
Тогда каждый из радиус-векторов точек системы получит элементарное приращение
Слайд 10ОБОБЩЁННЫЕ СИЛЫ
Обобщенные силы
Поскольку изменяется только координата , то
вычисляется как частный дифференциал
Тогда вычислим сумму элементарных работ всех действующих сил на рассматриваемом перемещении.
Слайд 1212
Обобщённые силы – это величины, равные коэффициентам при приращениях обобщённых
координат в
выражении полной элементарной работы
действующих на систему сил.
действующих на систему сил.
Размерность обобщённой силы равна размерности работы, деленной на размерность соответствующей обобщённой координаты.
Обобщенные силы
Если системе сообщить такое возможное перемещение, при котором одновременно меняются все обобщенные координаты, то сумма элементарных работ приложенных сил на этом перемещении равна:
