- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Уравнение глобального освещения презентация
Содержание
- 1. Уравнение глобального освещения
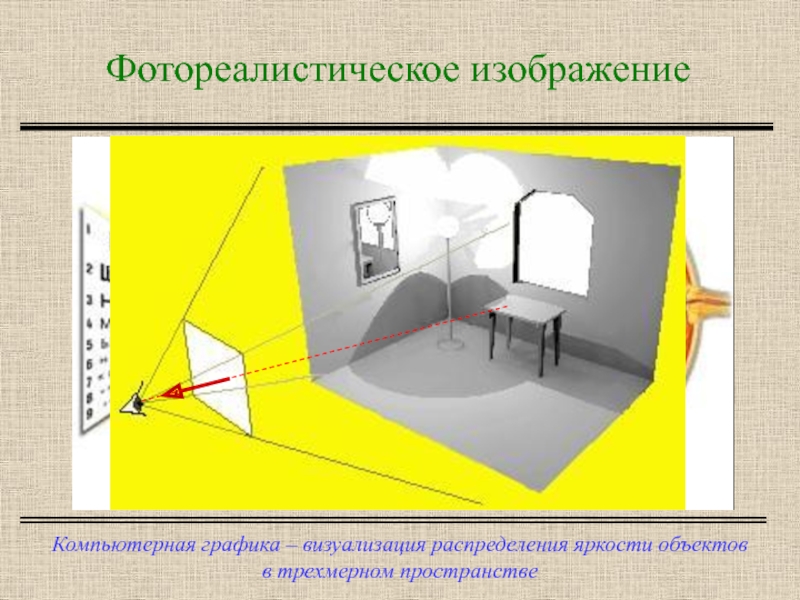
- 2. Фотореалистическое изображение Компьютерная графика – визуализация распределения яркости объектов в трехмерном пространстве
- 3. Яркость объекта при глобальном освещении Описание отражения
- 4. Коэффициент отражения и коэффициент яркости
- 5. Уравнение глобального освещения (УГО) Интегральное уравнение глобального
- 6. УГО как краевая задача УПИ Bidirectional Scattering
- 7. Интегральные уравнения Искомая функция под знаком интеграла
- 8. Методы решения интегральных уравнений Основной путь решения численный методом дискретизации на основе замены интеграла квадратурой
- 9. Трассировка лучей (Ray Tracing) Главный недостаток трассировки
- 10. Метод излучательности (Radiosity) Впервые метод предложен в
Слайд 1Уравнение глобального освещения
?: +7 (495) 763-5239 BudakVP@mpei.ru
Будак Владимир Павлович,
НИУ «МЭИ»
кафедра светотехники
Слайд 2Фотореалистическое изображение
Компьютерная графика – визуализация распределения яркости объектов
в трехмерном пространстве
Слайд 3Яркость объекта при глобальном освещении
Описание отражения в фотометрии
BRDF (Bidirectional Reflectance Distribution
Слайд 5Уравнение глобального освещения (УГО)
Интегральное уравнение глобального освещения (визуализации) Поляк Г.Л., 1960,
Яркость L вдоль луча не меняется
Зрачковая функция Θ (r,r′) – решение вопросов затенения:
Слайд 6УГО как краевая задача УПИ
Bidirectional Scattering Distribution Function – коэффициент яркости
Слайд 7Интегральные уравнения
Искомая функция под знаком интеграла – интегральное уравнение
Уравнение глобального освещения
– ядро интегрального уравнения
Слайд 8Методы решения интегральных уравнений
Основной путь решения численный методом дискретизации на основе
Слайд 9Трассировка лучей (Ray Tracing)
Главный недостаток трассировки лучей – огромный объем вычислительной
Численное решение интегральных уравнений – замена интеграла суммой → СЛАУ:
Точность решения → мелкая сетка → метод последовательных приближений:
физически это эквивалентно разложению по кратностям рассеяния и построению лучей в пространстве:
обратный ход лучей
все лучи дают вклад в изображение
трудно попасть в источник
только один ракурс
прямой ход лучей
формирование 3М изображения
трудно попасть в камеру
часть лучей формирует изображение
Слайд 10Метод излучательности (Radiosity)
Впервые метод предложен в работе Z.Yamauti в 1926,
полная теория
Наилучший метод ускорения сходимости переход к конечным пучкам – усреднение по углу и пространству → медленная угловая зависимость яркости
Наиболее эффективен такой подход при диффузных поверхностях
трехмерное изображение
приемлемое качество за доступное время
высокая точность расчета освещенности
отсутствие зеркальных отражений