- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Упругие волны в твердом теле. Теория упругости презентация
Содержание
- 1. Упругие волны в твердом теле. Теория упругости
- 2. Теория упругости: некоторые понятия Механическое напряжение в
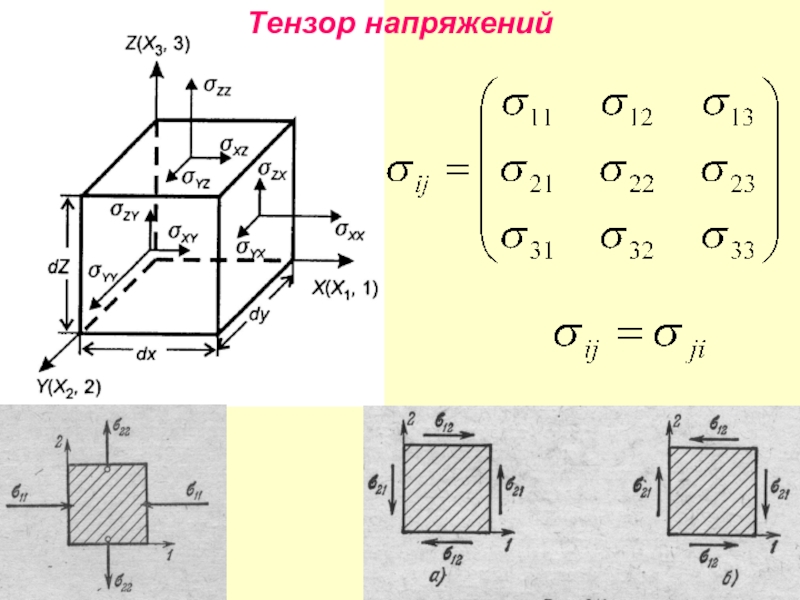
- 3. Тензор напряжений
- 4. Тензор напряжений Для любой точки абсолютно упругого
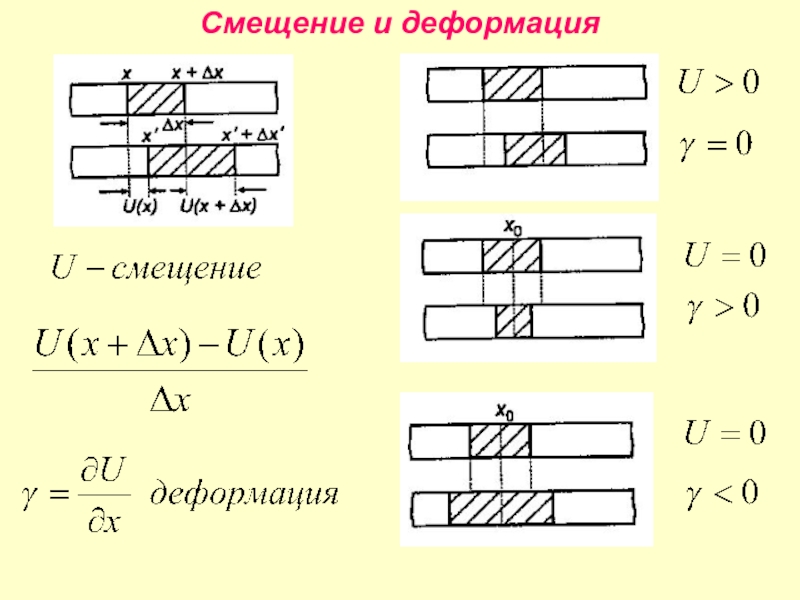
- 5. Смещение и деформация
- 6. Деформации по направлению осей Нормальные компоненты
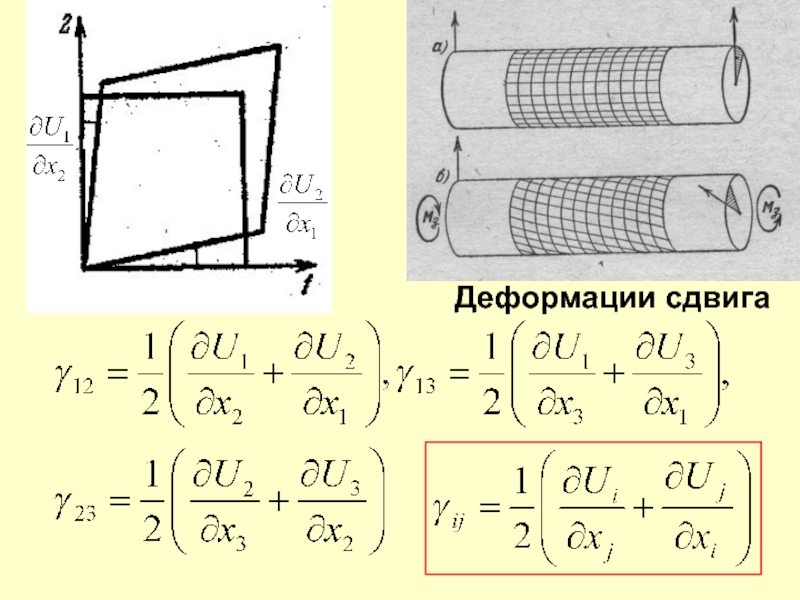
- 7. Деформации сдвига
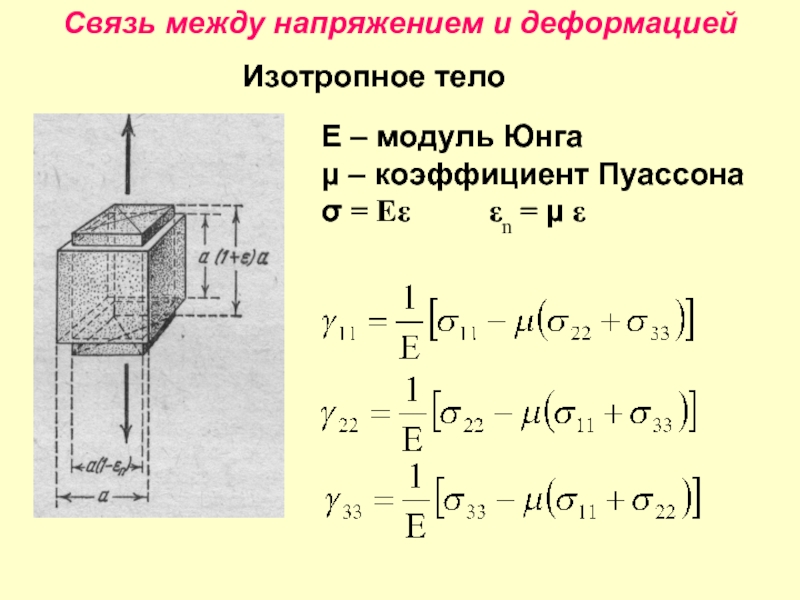
- 8. Связь между напряжением и деформацией Изотропное тело
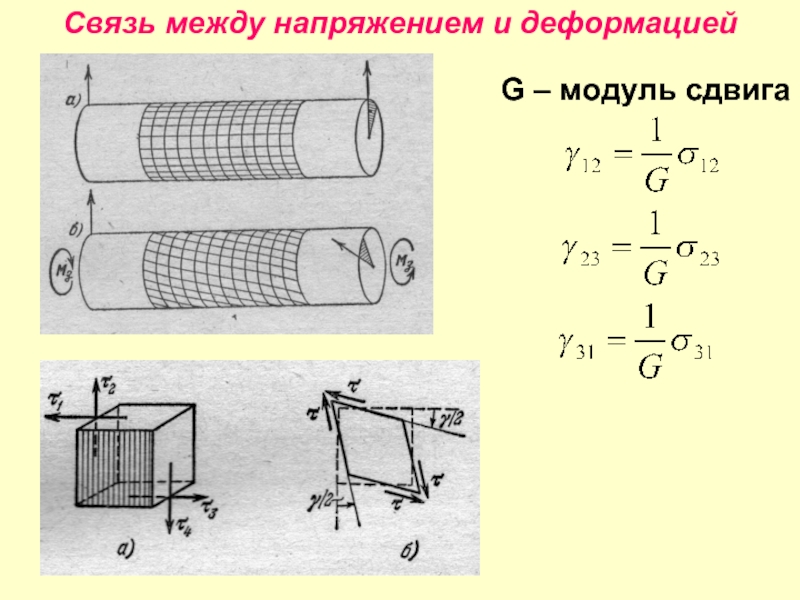
- 9. Связь между напряжением и деформацией G – модуль сдвига
- 10. Связь между напряжением и деформацией σ =
- 11. Связь между напряжением и деформацией
- 12. Связь между напряжением и деформацией В изотропном теле G = E/2(1 + μ)
- 13. Связь между напряжением и деформацией 81
- 14. Изотропные тела С44= 0,5 (С11 + С12) Волны Тензор пьезоэлектрических постоянных
- 15. Фононные возбуждения в твердом теле.
- 16. Квазичастицы Твердое тело сложная система, состоящая из
- 17. Колебательные свойства кристаллов M·d2 un /dt2 =
- 18. Колебательные свойства кристаллов un`=A exp(i(k`an-ωt)) =A exp(i(k
- 19. Колебательные свойства кристаллов Узлы n заняты ионами
- 20. Колебательные свойства кристаллов M·d2 un /dt2 =
- 21. Колебательные свойства кристаллов A / B =(
- 22. Колебательные свойства кристаллов Введем обозначение 16( f2
- 23. Колебательные свойства кристаллов ω2 ≈ω0(1 - (γka)2/32)
- 24. Колебательные свойства кристаллов В окрестности k=0 ω2
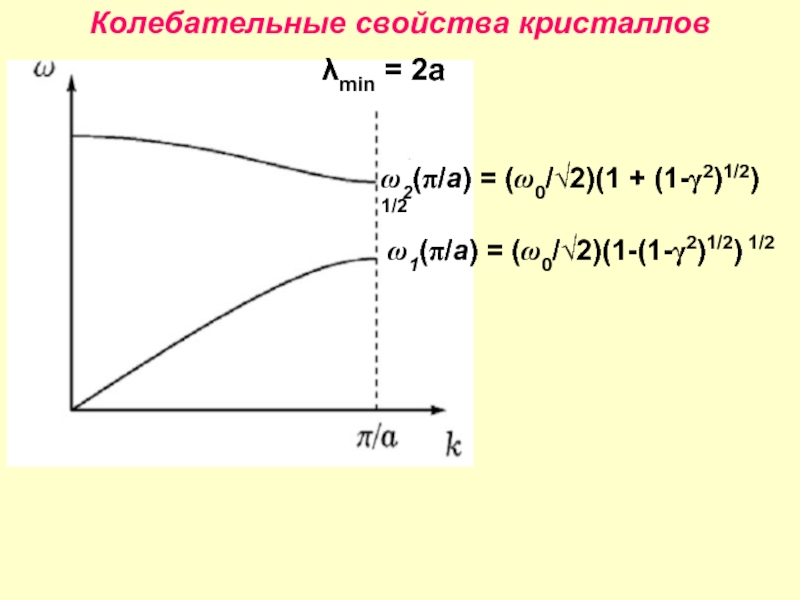
- 25. Колебательные свойства кристаллов ω1(π/a) = (ω0/√2)(1-(1-γ2)1/2) 1/2
- 26. Увлечение электронов акустическими фононами Смещение иона
- 27. Увлечение электронов акустическими фононами в металлах
- 28. Акустоэлектрический эффект Заряды накапливаются на краях
- 29. Акустоэлектрический эффект Заряды накапливаются на краях
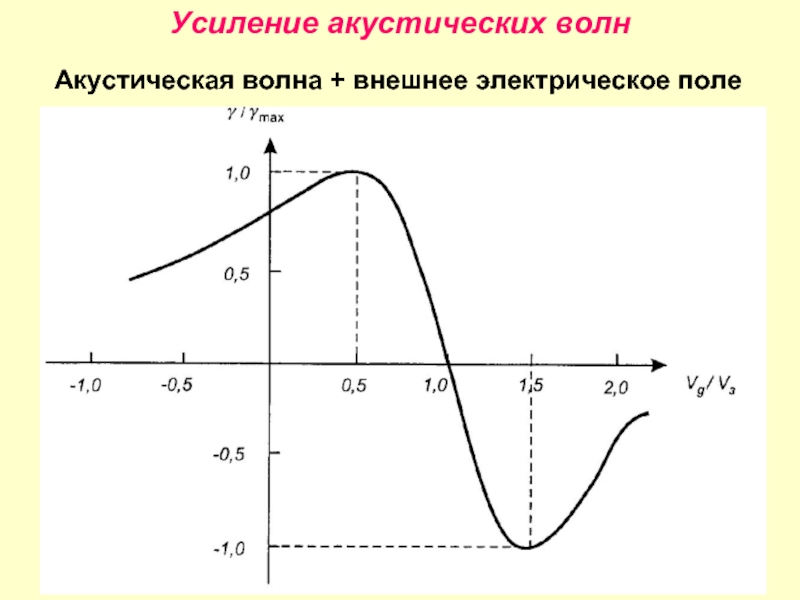
- 30. Усиление акустических волн Акустическая волна + внешнее электрическое поле
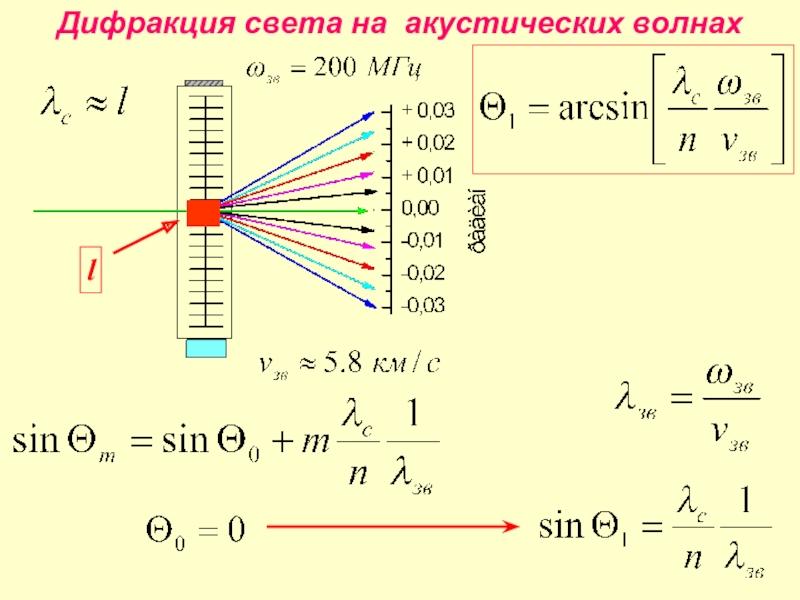
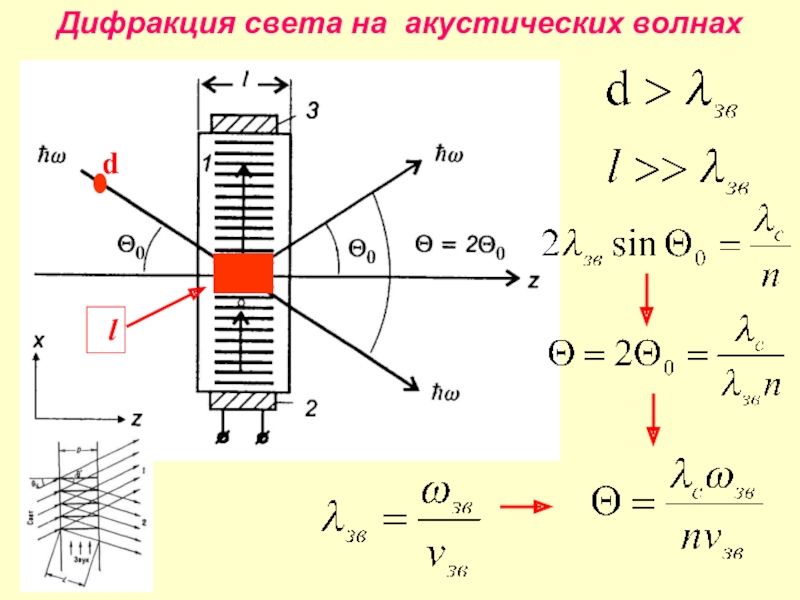
- 31. Дифракция света на акустических волнах
- 32. Дифракция света на акустических волнах
Слайд 2Теория упругости: некоторые понятия
Механическое напряжение в т.т. –
Сила действующая между двумя
σn = dFn /d S σt = dFt /d S
Fn проекция на нормаль к S
Ft проекция на плоскость касательную к S
n = 1,2,3
Слайд 4Тензор напряжений
Для любой точки абсолютно упругого тела существует
декартовая система координат
Слайд 8Связь между напряжением и деформацией
Изотропное тело
E – модуль Юнга
μ – коэффициент
σ = Eε εn = μ ε
Слайд 13Связь между напряжением и деформацией
81 компонента
21 независимая компонента
12, 21 → 6
13, 31 → 5
23, 32 → 4
С1122 → С12
С1123 → С14
Слайд 16Квазичастицы
Твердое тело сложная система, состоящая из сильно взаимодействующих частиц электронов и
Для преодоления сложностей, возникающих при описании большого количества взаимодействующих частиц, была предложена концепция квазичастиц. В основе этой концепции лежит попытка описать твердое тело в виде суммы независимых друг от друга согласованных движений многих (или даже всех) составляющих это тело частиц.
Слайд 17Колебательные свойства кристаллов
M·d2 un /dt2 = - f ·( un -
M·d2 un /dt2 = f ·( un+1 + un-1 - 2 ·un)
u(x,t)=A·exp(i(kx-ωt))
un=A·exp(i(kan-ωt))
-Mω2 = - f ·{2 - exp(-ika) - exp(ika)} =
- 2 ·f ·{1- cos(ka)} = 4·f ·sin2(ka/2)
ω2 =4·( f / M) ·sin2(ka/2), -> ω =ωmax ·|sin(ka/2)|
ω max =2·( f / M)1/2
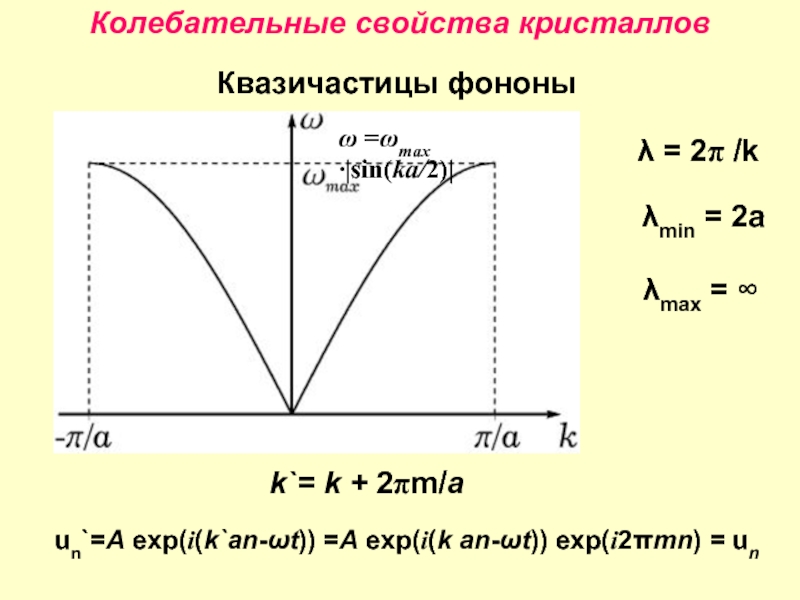
Слайд 18Колебательные свойства кристаллов
un`=A exp(i(k`an-ωt)) =A exp(i(k an-ωt)) exp(i2πmn) = un
k`=
Квазичастицы фононы
λ = 2π /k
λmin = 2a
λmax = ∞
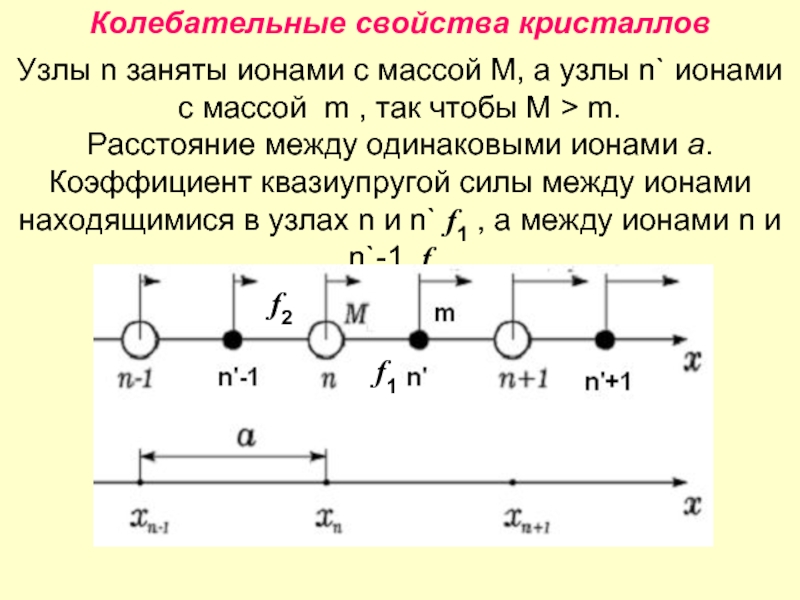
Слайд 19Колебательные свойства кристаллов
Узлы n заняты ионами с массой M, а узлы
Расстояние между одинаковыми ионами а. Коэффициент квазиупругой силы между ионами находящимися в узлах n и n` f1 , а между ионами n и n`-1 f2.
Слайд 20Колебательные свойства кристаллов
M·d2 un /dt2 = - f2 ·( un -
m·d2 un` /dt2 = - f2 ·( un` - un+1) + f1 ·( un - un`)
un = A exp(i(kan - ωt )) un-1 = un exp(-ika)
un` = B exp(i(kan - ωt )) un+1 = un exp(ika) un` = (B /A) un
-A · (ω2 - ( f2 + f1 ) / M )= B· ( f1 + f2· exp(-ika))/ M
-B · (ω2 - ( f2 + f1 ) / m )= A · ( f1 + f2· exp(ika))/ m
Слайд 21Колебательные свойства кристаллов
A / B =( f1+ f2· exp(-ika))/(( f2 +
=(( f2 + f1 ) - mω2 )/( f1 + f2· exp(ika ))
пусть ω02 = ( f2 + f1 )( M + m)/( Mm)
ω 21,2 = (ω02/2)(1 ±{1 - 16( f2 f1 /ω04 )sin2(ka/2)}1/2
Слайд 22Колебательные свойства кристаллов
Введем обозначение
16( f2 f1 /ω04) = 16 { Mm
ω21 = (ω02/2)(1 - {1 - γ2sin2(ka/2)} 1/2)
ω22 = (ω02/2)(1 + {1 - γ2sin2(ka/2)} 1/2)
-π/a ω1(0) = 0; акустические фононы ω2(0) =ω0; оптические фононы ω2(0) =ω0 >ω2(π/a) > ω1(π/a) > ω1(0)
ω1(π/a) = (ω0/√2)(1-(1-γ2)1/2) 1/2
ω2(π/a) = (ω0/√2)(1 + (1-γ2)1/2) 1/2
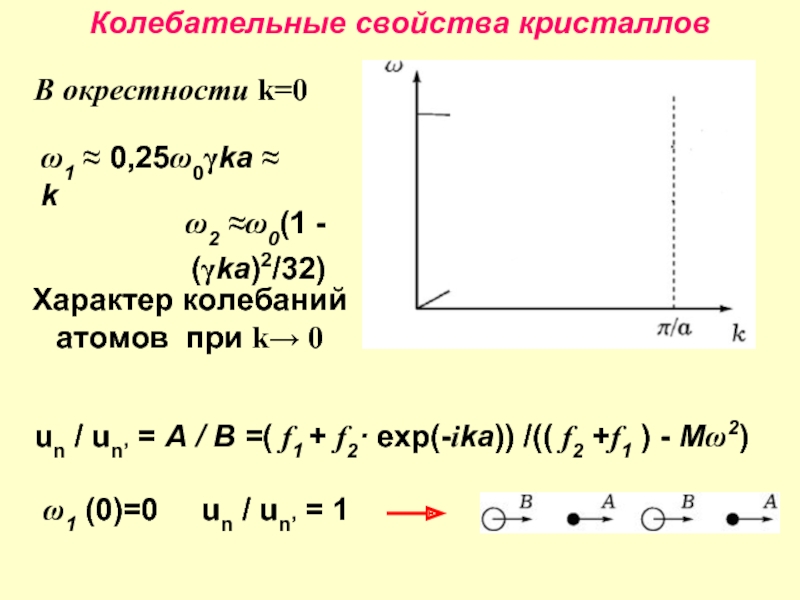
Слайд 23Колебательные свойства кристаллов
ω2 ≈ω0(1 - (γka)2/32)
Характер колебаний
атомов при k→ 0
un
ω1 (0)=0 un / un’ = 1
ω21 = (ω02/2)(1 - {1 - γ2sin2(ka/2)} 1/2)
ω22 = (ω02/2)(1 + {1 - γ2sin2(ka/2)}1/2)
В окрестности k=0
ω1 ≈ 0,25ω0γka ≈ k
Слайд 24Колебательные свойства кристаллов
В окрестности k=0
ω2 = ω0
un / un’ = A
un / un’ =(f1 + f2) /((f2 +f1 )- Mω02) =
(f1 + f2) /((f2 +f1 )- (f2 +f1 )( M + m)/( m)) =
=1/(1 - ( M + m)/ m) = - m/M
un M + un’ m = 0
ω02 = ( f2 + f1 )( M + m)/( Mm)
Слайд 25Колебательные свойства кристаллов
ω1(π/a) = (ω0/√2)(1-(1-γ2)1/2) 1/2
ω2(π/a) = (ω0/√2)(1 + (1-γ2)1/2)
λmin = 2a
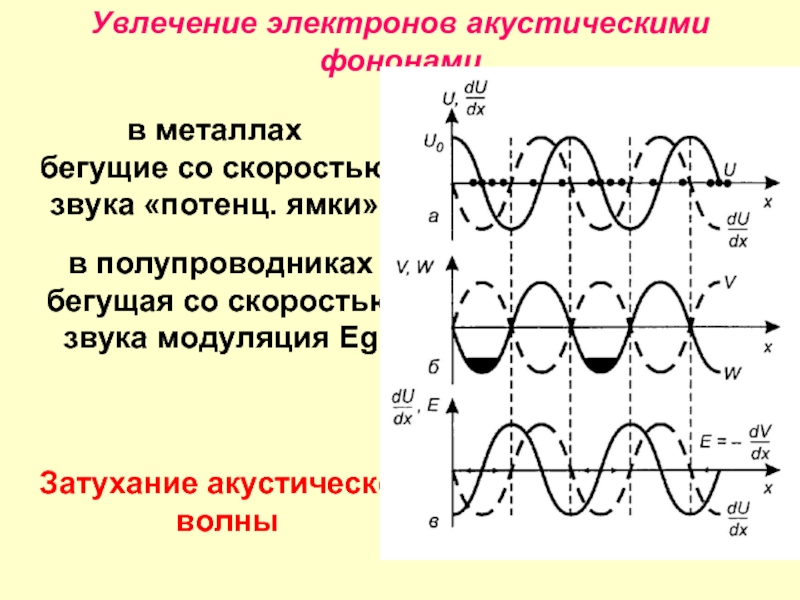
Слайд 26Увлечение электронов акустическими фононами
Смещение иона U=U0·cos(ωt- kx)
Деформация dU/dx= U0k·sin(ωt- kx)
Появляются
Изменяется плотность заряда
Изменяется распределение потенциала V и потенциальная энергия эл-на. e
W(x) = - eV(x)
Появляется
Электрическое поле
E = -dV/dx
Бегущая эл. волна!!!
Слайд 27Увлечение электронов акустическими фононами
в металлах
бегущие со скоростью
звука «потенц. ямки»
в
бегущая со скоростью
звука модуляция Eg
Затухание акустической
волны
Слайд 28Акустоэлектрический эффект
Заряды накапливаются на краях полупроводника
возникает эл. поле E
Поток фононов
Поток энергии W=nq vзв ωq
Поток импульса p=W/ vзв =nq ωq
Электроны получают импульс E= γ W/ enevзв = γ μW/ σ vзв
γ Wdx / vзв ≡