- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Упругие волны. Электромагнитные волны презентация
Содержание
- 1. Упругие волны. Электромагнитные волны
- 2. Общая физика. «Волны» Упругие волны Упругая
- 3. Общая физика. «Волны» Упругие волны Волновая
- 4. Общая физика. «Волны» Упругие волны
- 5. Общая физика. «Волны» Упругие волны
- 6. Общая физика. «Волны» Упругие волны
- 7. Общая физика. «Волны» Упругие волны Уравнения плоской и сферической волн.
- 8. Общая физика. «Волны» После преобразований: Упругие
- 9. Общая физика. «Волны» Упругие волны Уравнения
- 10. Общая физика. «Волны» Упругие
- 11. Общая физика. «Волны» Упругие волны Волновое
- 12. Общая физика. «Волны» Упругие волны Звуковые
- 13. Общая физика. «Волны» Электромагнитные волны.
- 14. Общая физика. «Волны» Электромагнитные волны. В
- 15. Общая физика. «Волны» Электромагнитные волны. В
- 16. Общая физика. «Волны» Электромагнитные волны. Рассмотрим
- 17. Общая физика. «Волны» Электромагнитные волны. Волновые
- 18. Общая физика. «Волны» Электромагнитные волны. Мгновенная картина электромагнитной волны в некоторый момент времени:
- 19. Общая физика. «Волны» Электромагнитные волны. Энергия
- 20. Общая физика. «Волны» Электромагнитные волны.
- 21. Общая физика. «Волны» Электромагнитные волны. Интенсивность
Слайд 1Общая физика. «Волны»
ЛЕКЦИЯ 10
ПЛАН ЛЕКЦИИ
1. Упругие волны:
- волновое уравнение;
- звуковые волны. Эффект Доплера (самостоятельно).
2. Электромагнитные волны:
- волновое уравнение;
- энергия электромагнитной волны;
- интенсивность;
- импульс электромагнитной волны.
Слайд 2Общая физика. «Волны»
Упругие волны
Упругая волна - процесс распространения возмущения в
Основные виды волн:
упругие (например, звуковые и сейсмические волны);
волны на поверхности жидкости;
электромагнитные волны (в том числе световые и радиоволны).
Характерная особенность волн - при их распространении происходит перенос энергии без переноса вещества.
Гармоническая волна - изменение состояния среды происходит по закону синуса или косинуса.
Параметры упругих гармонических волн
Фронт волны (волновой фронт) - геометрическое место точек, до которых доходят колебания к некоторому моменту времени t.
Слайд 3Общая физика. «Волны»
Упругие волны
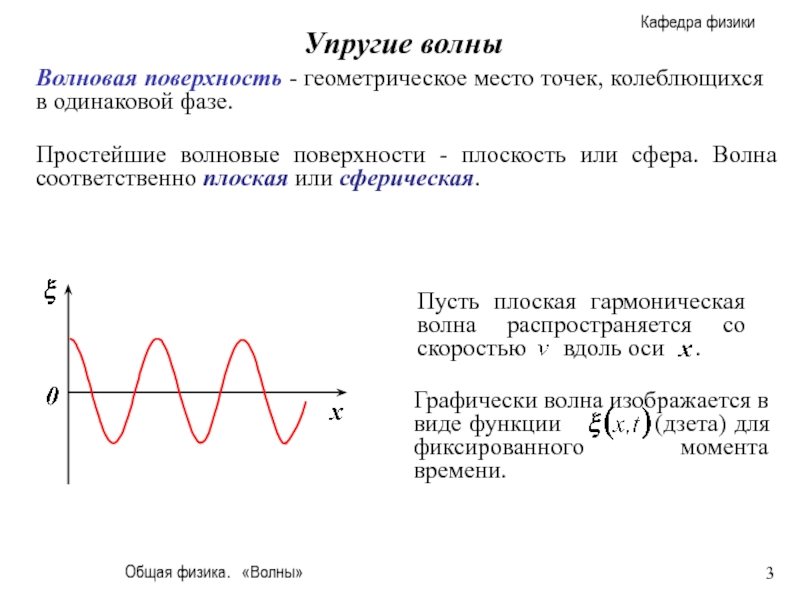
Волновая поверхность - геометрическое место точек, колеблющихся
Простейшие волновые поверхности - плоскость или сфера. Волна соответственно плоская или сферическая.
Слайд 4Общая физика. «Волны»
Упругие волны
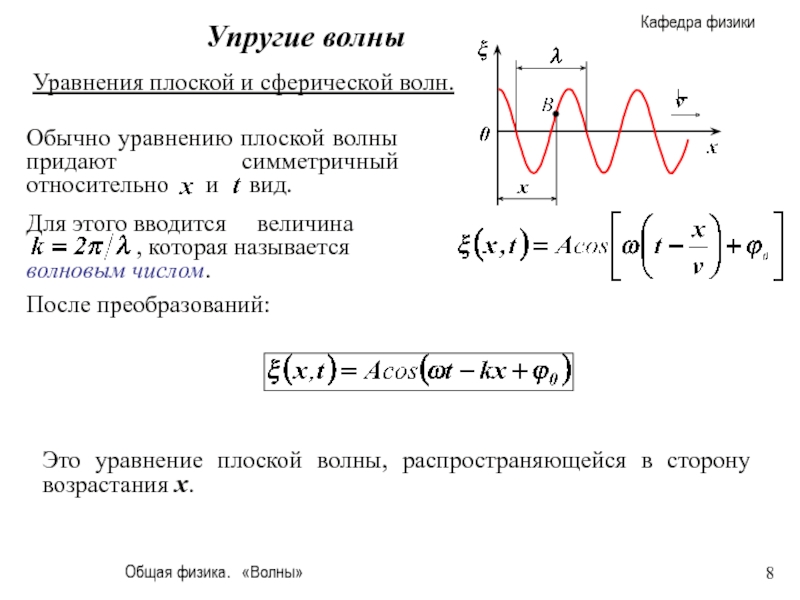
х - это расстояние от источника колебаний
Рисунок дает мгновенную картину распределения возмущений вдоль направления распространения волны.
Слайд 5Общая физика. «Волны»
Упругие волны
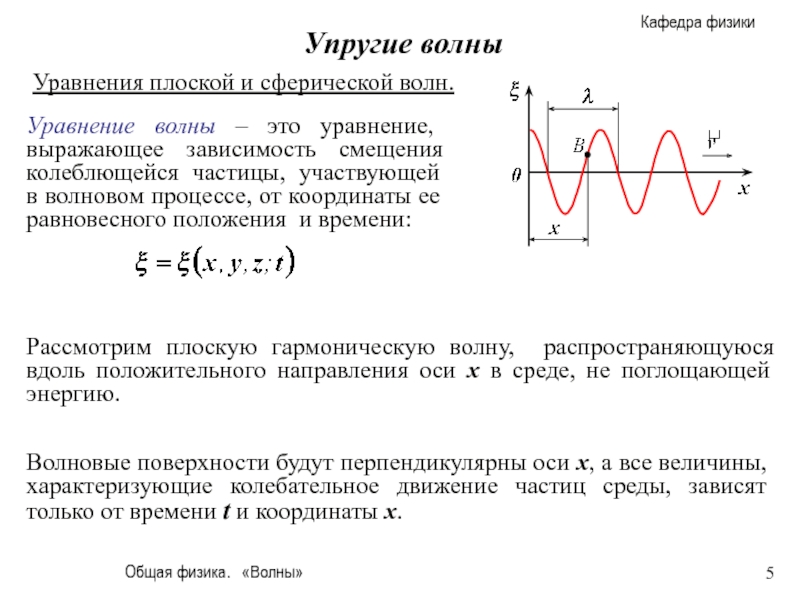
Уравнения плоской и сферической волн.
Уравнение волны
Рассмотрим плоскую гармоническую волну, распространяющуюся вдоль положительного направления оси х в среде, не поглощающей энергию.
Волновые поверхности будут перпендикулярны оси х, а все величины, характеризующие колебательное движение частиц среды, зависят только от времени t и координаты х.
Слайд 6Общая физика. «Волны»
Упругие волны
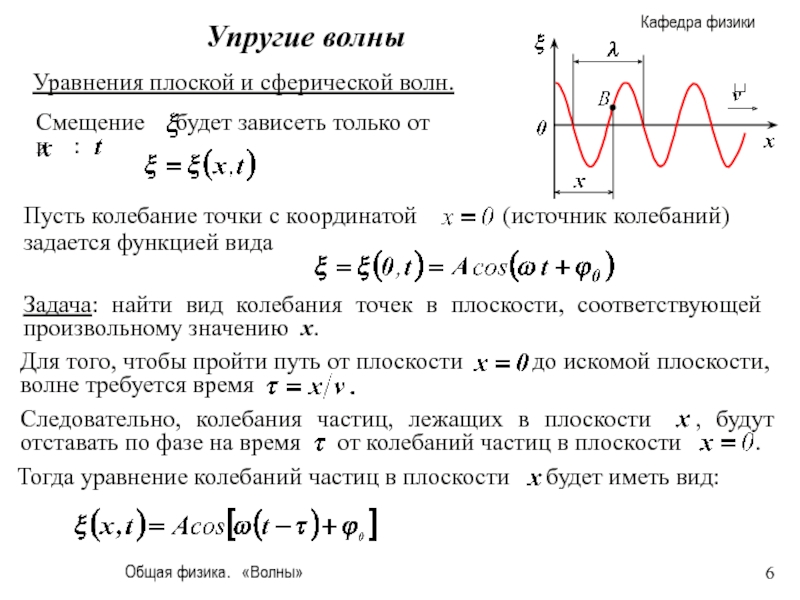
Уравнения плоской и сферической волн.
Задача: найти
Слайд 8Общая физика. «Волны»
После преобразований:
Упругие волны
Уравнения плоской и сферической волн.
Это
Слайд 9Общая физика. «Волны»
Упругие волны
Уравнения плоской и сферической волн.
Будем считать
Волна от такого источника в изотропной и однородной среде будет сферической.
Уравнение сферической волны.
Следовательно, уравнение сферической волны имеет вид:
Слайд 10Общая физика. «Волны»
Упругие волны
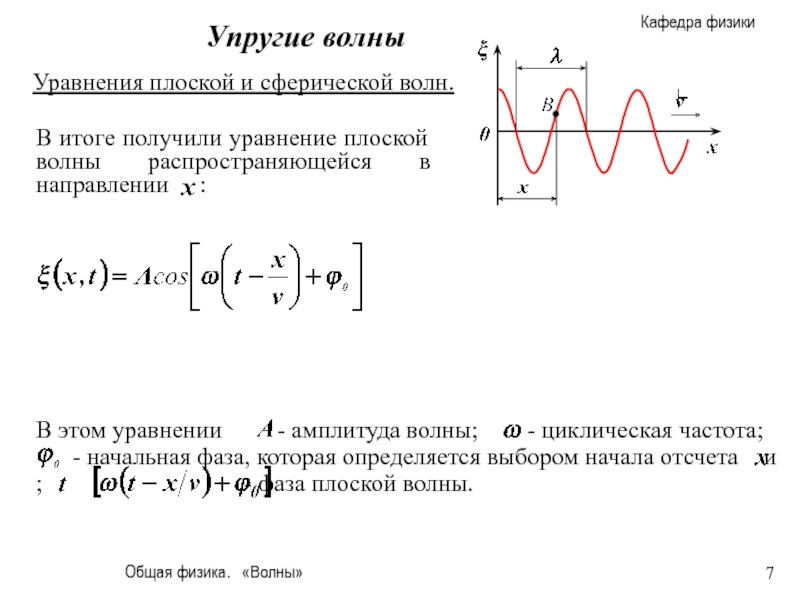
Уравнения плоской и сферической волн.
Уравнение плоской
Уравнение сферической волны
Слайд 11Общая физика. «Волны»
Упругие волны
Волновое уравнение.
Все возможные волны описываются волновыми уравнениями.
Уравнение конкретной волны - это решение волнового уравнения.
Вид волнового уравнения:
- оператор набла (оператор Лапласа)
Волновому уравнению удовлетворяют уравнения плоской и сферической волн.
Это одномерное волновое уравнение второго порядка в частных производных.
Слайд 12Общая физика. «Волны»
Упругие волны
Звуковые волны (звук) – это распространяющийся в
Диапазон звуковых частот – 20 Гц – 20 кГц.
Инфразвук - волны с частотами меньше 20 Гц.
Ультразвук - волны с частотами больше 20 кГц
Звуковые волны.
Акустика - учение о звуке.
Эффект Доплера.
Изучить самостоятельно!
Слайд 13Общая физика. «Волны»
Электромагнитные волны.
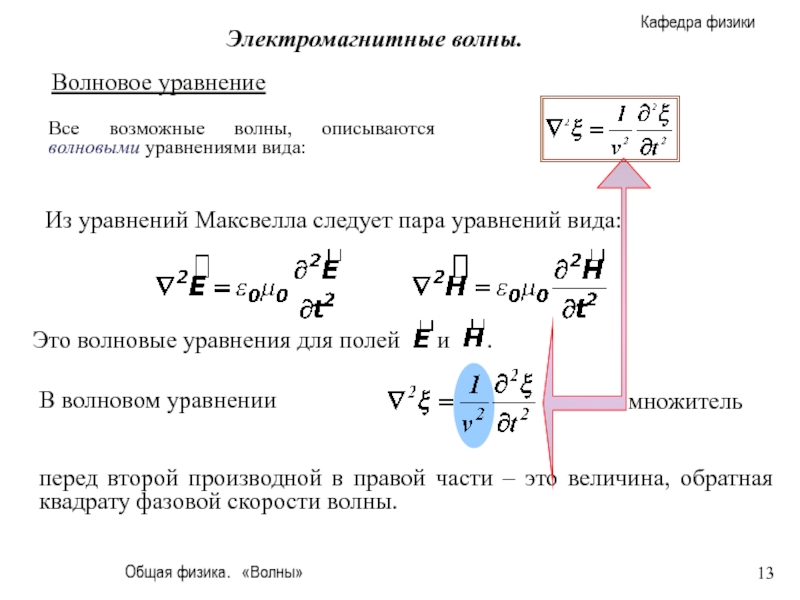
Из уравнений Максвелла следует пара уравнений вида:
Волновое
В волновом уравнении
множитель
перед второй производной в правой части – это величина, обратная квадрату фазовой скорости волны.
Все возможные волны, описываются волновыми уравнениями вида:
Слайд 14Общая физика. «Волны»
Электромагнитные волны.
В вакууме эта скорость для электромагнитной волны
Волновое уравнение
Эти уравнения указывают на то, что электромагнитные поля могут существовать в виде электромагнитных волн, фазовая скорость которых в вакууме равна скорости света.
Слайд 15Общая физика. «Волны»
Электромагнитные волны.
В природе существуют только правовинтовые электромагнитные волны
Это одно из проявлений законов взаимного создания переменных магнитных и электрических полей.
Векторная структура электромагнитной волны.
Слайд 16Общая физика. «Волны»
Электромагнитные волны.
Рассмотрим для простоты вид и свойства одномерного
Слайд 17Общая физика. «Волны»
Электромагнитные волны.
Волновые уравнения такой волны будут иметь вид:
Этим
Слайд 18Общая физика. «Волны»
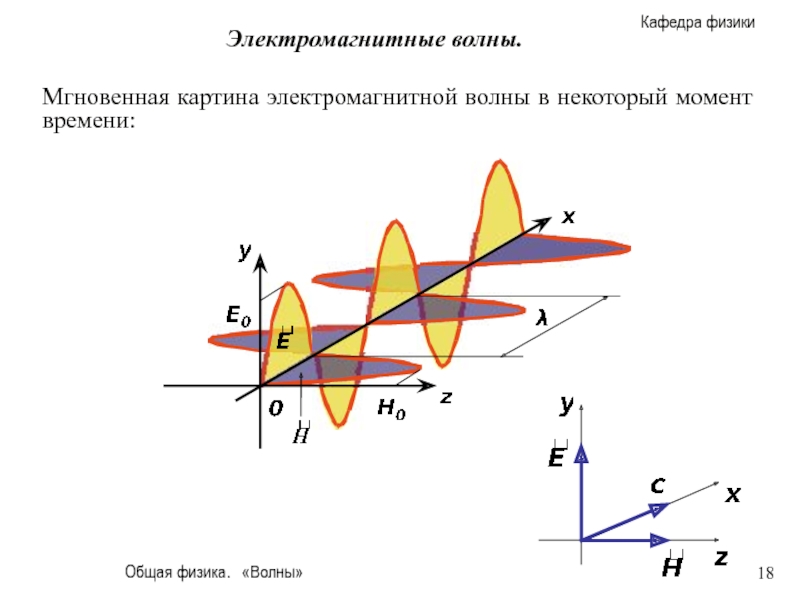
Электромагнитные волны.
Мгновенная картина электромагнитной волны в некоторый момент
Слайд 19Общая физика. «Волны»
Электромагнитные волны.
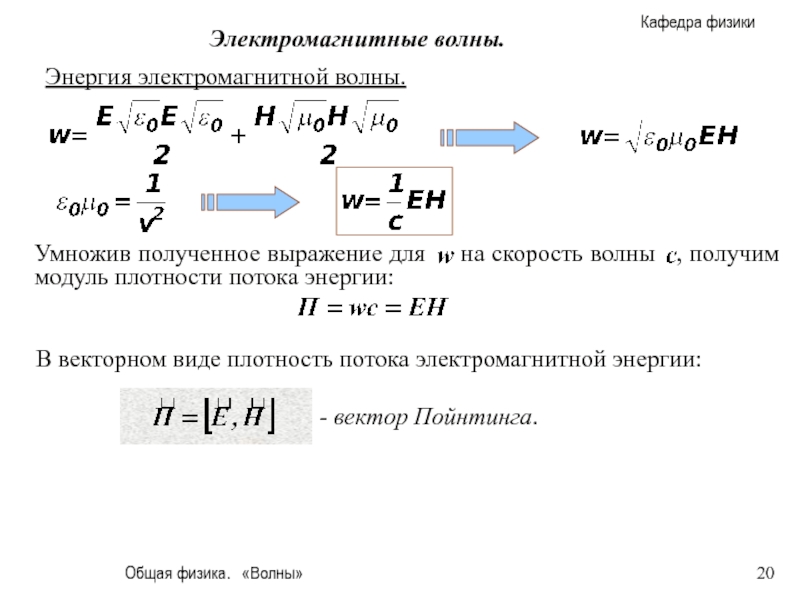
Энергия электромагнитной волны.
Электромагнитные волны переносят в пространстве
Объемная плотность энергии электромагнитной волны складывается из объемных плотностей энергии электрического и магнитного полей:
Следовательно, выражение для объемной плотности энергии электромагнитной волны в произвольный момент времени в рассматриваемой точке пространства можно представить в виде:
Слайд 20Общая физика. «Волны»
Электромагнитные волны.
Энергия электромагнитной волны.
В векторном виде плотность потока
- вектор Пойнтинга.
Слайд 21Общая физика. «Волны»
Электромагнитные волны.
Интенсивность электромагнитной волны.
Импульс электромагнитной волны.
Перенос энергии электромагнитной
Запишем это выражение для плотностей импульса и энергии т.е., для величин, отнесенных к единице объема: