- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Упругие напряжения и обратимые деформации. (Лекция 10) презентация
Содержание
- 1. Упругие напряжения и обратимые деформации. (Лекция 10)
- 2. Принцип напряжений Коши и Эйлера: В каждом
- 4. Девять компонент тензора напряжений могут быть
- 5. Напряженным состоянием в точке называется совокупность напряжений,
- 8. Правило знаков: Растягивающие нормальные напряжения будем считать
- 10. (20) вектор относительного смещения (21) (22) Ряд
- 11. Тензор дисторсии (как и всякий тензор) может
- 12. Разложение тензора малых деформаций Как и всякий
- 15. Эта величина относительного изменения объема не зависит
- 16. Вектор поворота Пусть Тогда деформация элемента определяется
- 17. Найдем компоненты вектора смещений: или: вектор поворота
- 19. Закон Гука В технических расчетах деформацию стержня
- 22. Обобщенный закон Гука для анизотропного тела: Учитывая
- 23. 2.Рассмотрим в элементе объема сферу единичного радиуса,
- 25. Термодинамическая теория Уравнение Гиббса для простой деформируемой
- 26. Домножив (4) на плотность и проинтегрировав по
Слайд 1Лекции 10
Упругие напряжения и обратимые деформации
Тензор напряжений. Тензор деформаций. Закон
Соотношения Дюамеля-Неймана.
Термодинамическое обоснование уравнений теории упругости и термоупругости
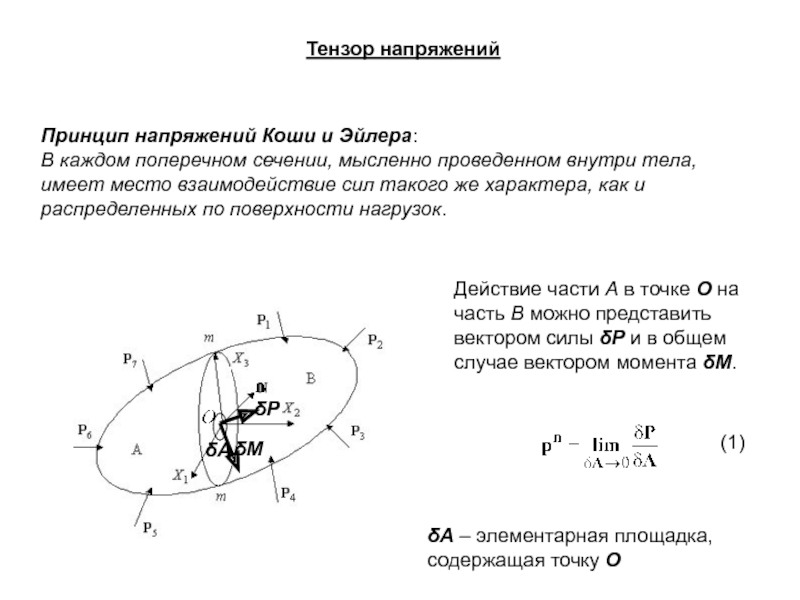
Слайд 2Принцип напряжений Коши и Эйлера:
В каждом поперечном сечении, мысленно проведенном внутри
Действие части А в точке O на часть В можно представить вектором силы δP и в общем случае вектором момента δM.
δА – элементарная площадка, содержащая точку О
(1)
Тензор напряжений
Слайд 4
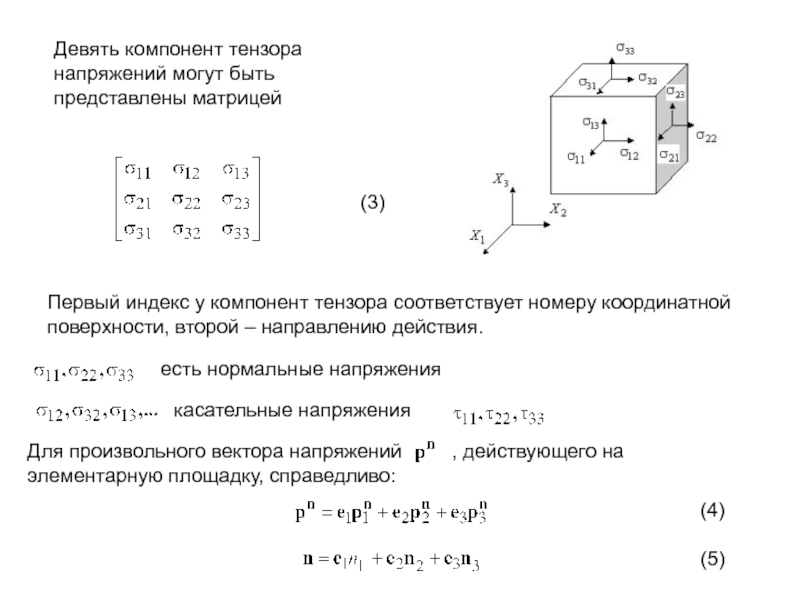
Девять компонент тензора напряжений могут быть представлены матрицей
Первый индекс у
(3)
(4)
(5)
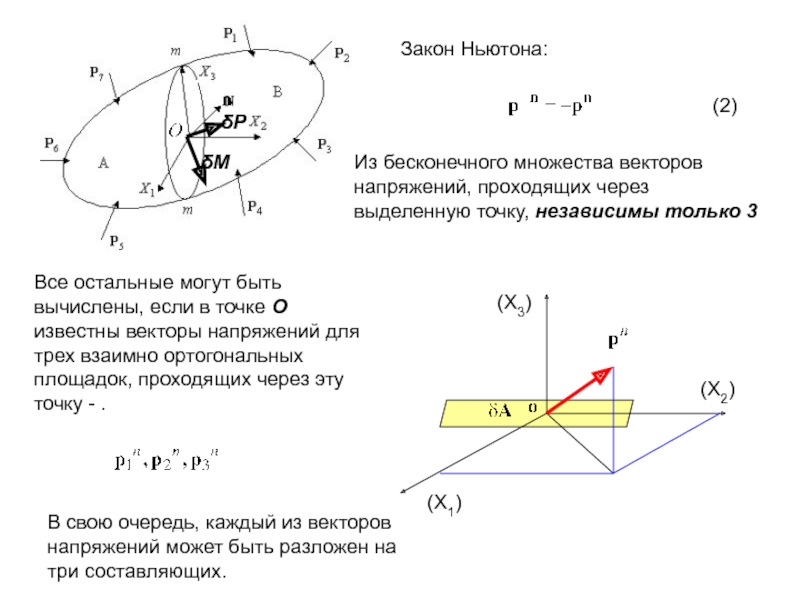
Слайд 5Напряженным состоянием в точке называется совокупность напряжений, действующих по всевозможным площадкам,
n1,n2,n3 – направляющие косинусы нормали
(6)
Повторяющийся индекс (i) называется немым (подставным); по нему идет суммирование. Неповторяющийся индекс (j) называется свободным
Слайд 7
антисимметричный тензор эквивалентен так называемому аксиальному вектору с компонентами
(14)
(15)
(16)
(17)
Слайд 8Правило знаков:
Растягивающие нормальные напряжения будем считать положительными, сжимающие – отрицательными.
Знак касательных
Слайд 10(20)
вектор относительного смещения
(21)
(22)
Ряд Тейлора:
относительные смещения малы по сравнению с абсолютными значениями
Сравниваем (21) и (22):
(23)
Тензор относительной деформации точки Q относительно точки P или тензор дисторсии
Компоненты этого тензора есть функции координат и времени!
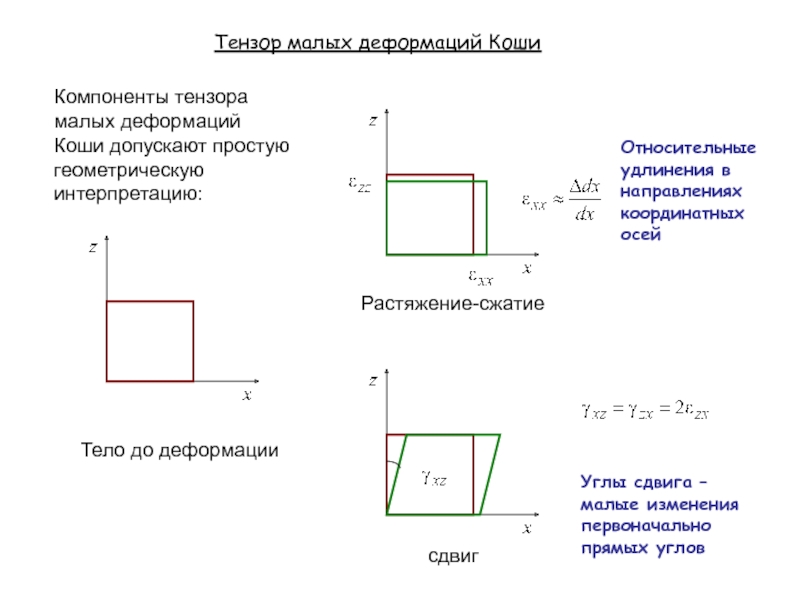
Слайд 11Тензор дисторсии (как и всякий тензор) может быть представлен в виде
Симметричная часть:
Тензор малых деформаций Коши
(23)
(24)
(25)
Тензор малых поворотов
Слайд 12Разложение тензора малых деформаций
Как и всякий тензор, тензор деформаций можно представить
(26)
(27)
(28)
(29)
…….
(13)
Шаровой тензор
Девиатор тензора деформаций
Тензор малых деформаций, по определению, симметричен!
Слайд 15Эта величина относительного изменения объема не зависит от выбора системы координат!
(33)
Иначе:
Если
Условие несжимаемости для деформируемой среды
МЖГ:
(34)
Компоненты вектора скорости
Слайд 16Вектор поворота
Пусть
Тогда деформация элемента определяется тензором вида:
или
Это –антисимметричный тензор, включающий только
(35)
(36)
Слайд 17Найдем компоненты вектора смещений:
или:
вектор поворота
(37)
(38)
Векторное произведение вектора поворота и вектора dr
Слайд 19Закон Гука
В технических расчетах деформацию стержня при растяжении определяют через относительное
Идеальная упругость – однозначная зависимость между силами и вызванными этими силами перемещениями
Для огромного большинства материалов закон упругости с большой точностью можно считать линейным
модуль упругости
Закон Гука
Закон упругости справедлив, пока напряжения не достигнут некоторого предела, называемого пределом упругости
Для всех материалов, применяемых в технике (кроме резины и каучукообразных полимеров), модуль упругости весьма высок по сравнению с пределом упругости, поэтому величина упругой деформации невелика – не более 1-2 %
Слайд 22Обобщенный закон Гука для анизотропного тела:
Учитывая связь (верхняя строка предыдущего слайда)
из
(41)
(42)
Тензоры напряжений и деформаций обладают рядом интересных свойств. Рассмотрим некоторые из них
Слайд 232.Рассмотрим в элементе объема сферу единичного радиуса, центр которой находится в
После деформации точки сферы будут иметь координаты:
и окажутся на поверхности, описываемой следующим уравнением
т.е., уравнение сферы переходит в уравнение эллипсоида, если все главные значения тензора деформаций – различны. Если главные значения – одинаковы, то сфера переходит в сферу.
В теории показывается (обычными средствами математического анализа), что точки, лежащие на одной прямой до деформации, после деформации также расположатся на некоторой прямой; параллельные прямые останутся параллельными и тд.
Слайд 25Термодинамическая теория
Уравнение Гиббса для простой деформируемой среды:
Локальным аналогом изменения удельного объема
Как перейти от (1) к термодинамической системе в целом?
Введем гидродинамической давление по формуле
(1)
Известно (для малых деформаций):
(2)
Если - шаровые тензоры, то
(3)
Слайд 26Домножив (4) на плотность и проинтегрировав по объему, получим
(4)
Уравнения Гиббса можно
Как мы уже знаем, если имеется уравнение Гиббса, то имеет место система УРС:
(5)
(6)
(7)