- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
University physics. Forces review of basic concepts презентация
Содержание
- 1. University physics. Forces review of basic concepts
- 2. Vectors and Scalars All physical quantities (e.g.
- 3. Representing Vectors An arrowed straight line is
- 4. Addition of vectors 1 The original vectors
- 5. Addition of vectors 2 With two vectors
- 6. 2 - Resultant of Two Forces
- 7. 2 - Addition of Vectors
- 8. 2 - Addition of Vectors
- 9. 2 - Resultant of Several Concurrent Forces
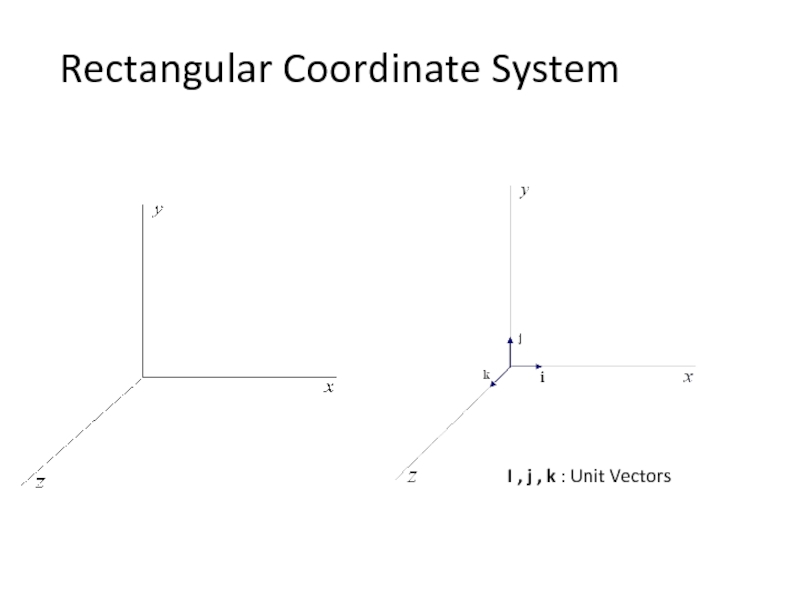
- 10. Rectangular Coordinate System I , j , k : Unit Vectors
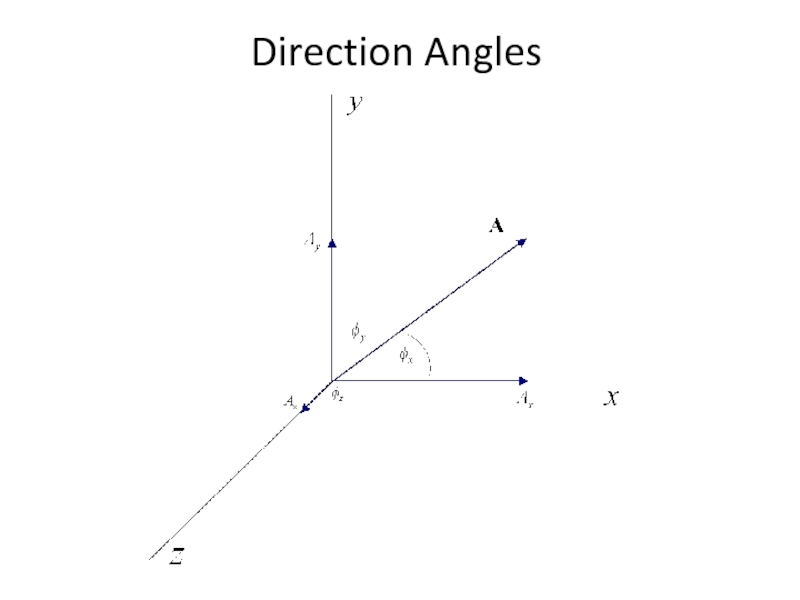
- 12. Direction Angles
- 13. Relationships for Direction Angles
- 14. Example 1. A force has x,
- 15. Determine the magnitude of the force in previous example:
- 16. Determine the three direction angles for the force :
- 18. Vector Operations to be Considered Scalar or
- 19. Consider two vectors A and B oriented in different directions.
- 20. Scalar or Dot Product Represents the Work
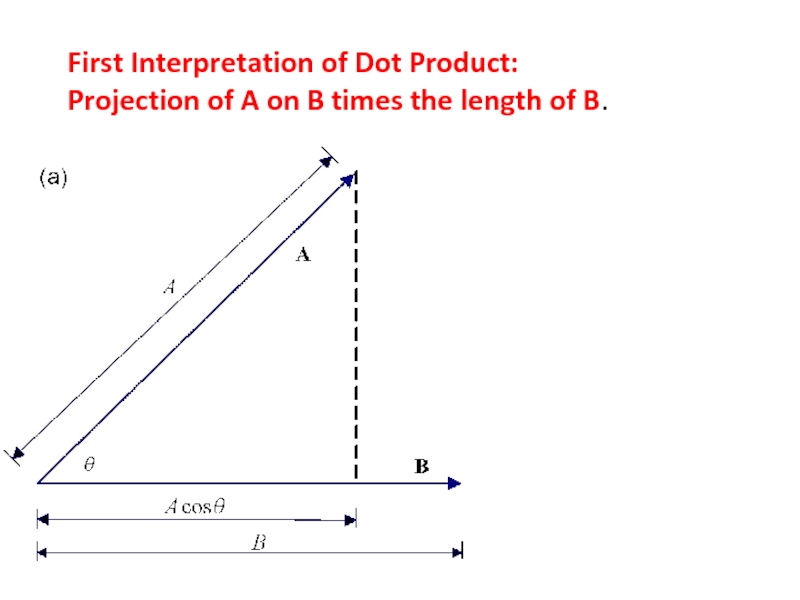
- 21. First Interpretation of Dot Product: Projection
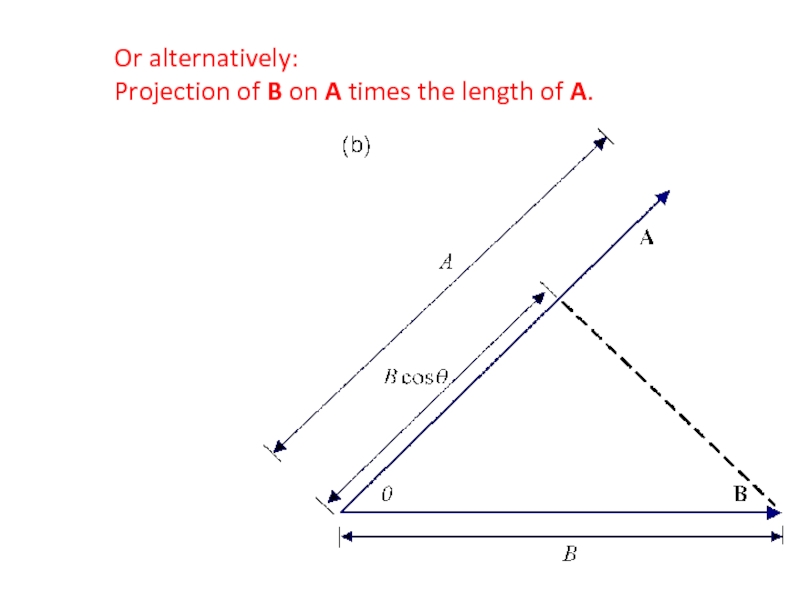
- 22. Or alternatively: Projection of B on A times the length of A.
- 23. Some Implications of Dot Product
- 24. Example : Perform several scalar operations on the following vectors:
- 26. Vector or Cross Product The Cross Product
Vectors and Scalars All physical quantities (e.g. speed and force) are described by a magnitude and a unit. VECTORS – also need to have their direction specified examples:
Слайд 2Vectors and Scalars
All physical quantities (e.g. speed and force) are described
by a magnitude and a unit.
VECTORS – also need to have their direction specified
examples: displacement, velocity, acceleration, force.
SCALARS – do not have a direction
examples: distance, speed, mass, work, energy.
VECTORS – also need to have their direction specified
examples: displacement, velocity, acceleration, force.
SCALARS – do not have a direction
examples: distance, speed, mass, work, energy.
Слайд 3Representing Vectors
An arrowed straight line is used.
The arrow indicates the direction
and the length of the line is proportional to the magnitude.
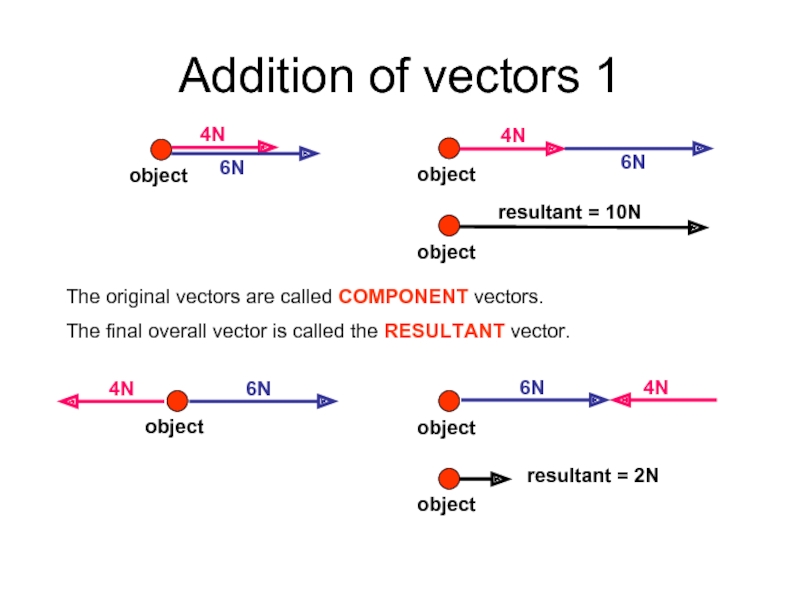
Слайд 4Addition of vectors 1
The original vectors are called COMPONENT vectors.
The final
overall vector is called the RESULTANT vector.
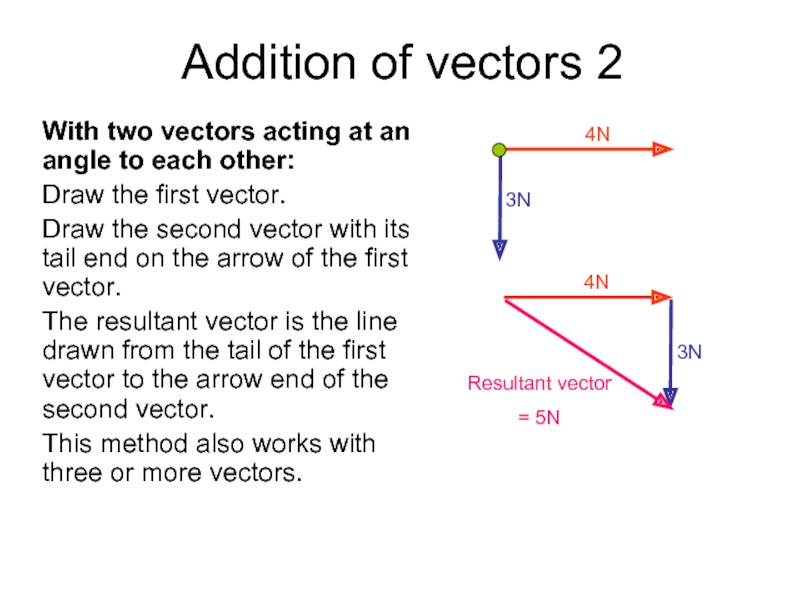
Слайд 5Addition of vectors 2
With two vectors acting at an angle to
each other:
Draw the first vector.
Draw the second vector with its tail end on the arrow of the first vector.
The resultant vector is the line drawn from the tail of the first vector to the arrow end of the second vector.
This method also works with three or more vectors.
Draw the first vector.
Draw the second vector with its tail end on the arrow of the first vector.
The resultant vector is the line drawn from the tail of the first vector to the arrow end of the second vector.
This method also works with three or more vectors.
Слайд 62 -
Resultant of Two Forces
The resultant is equivalent to the
diagonal of a parallelogram which contains the two forces in adjacent legs.
Force is a vector quantity.
Слайд 14Example 1. A force has x, y, and z components of
3, 4, and –12 N, respectively.
Express the force as a vector in rectangular coordinates.
Слайд 18Vector Operations to be Considered
Scalar or Dot Product:
A•B
Vector or Cross Product: AxB
Triple Scalar Product: (AxB)•C
Vector or Cross Product: AxB
Triple Scalar Product: (AxB)•C
Слайд 20Scalar or Dot Product
Represents the Work done by the Force B
during the
displacement A for example.
displacement A for example.
Слайд 26Vector or Cross Product
The Cross Product of 2 vectors A and
B, is a vector C
which is perpendicular to both A and B, and whose
Amplitude is (AB sin(θ))
which is perpendicular to both A and B, and whose
Amplitude is (AB sin(θ))
