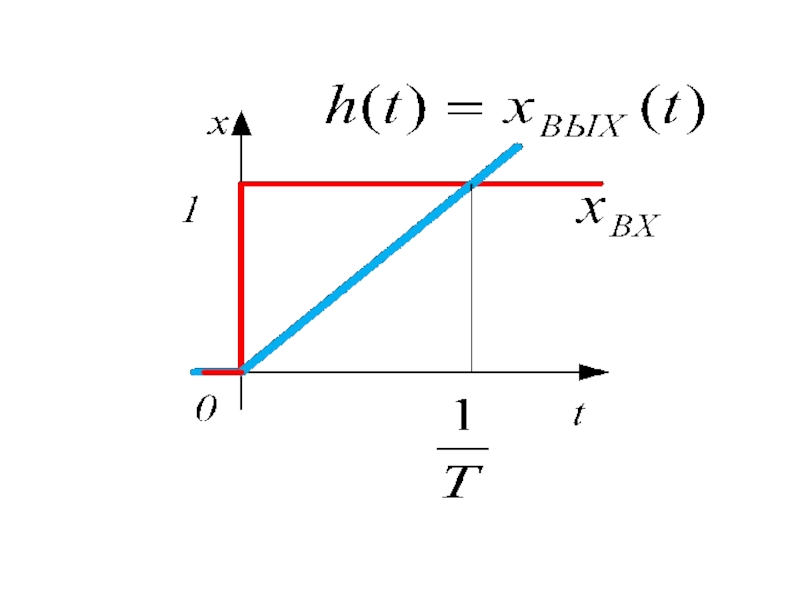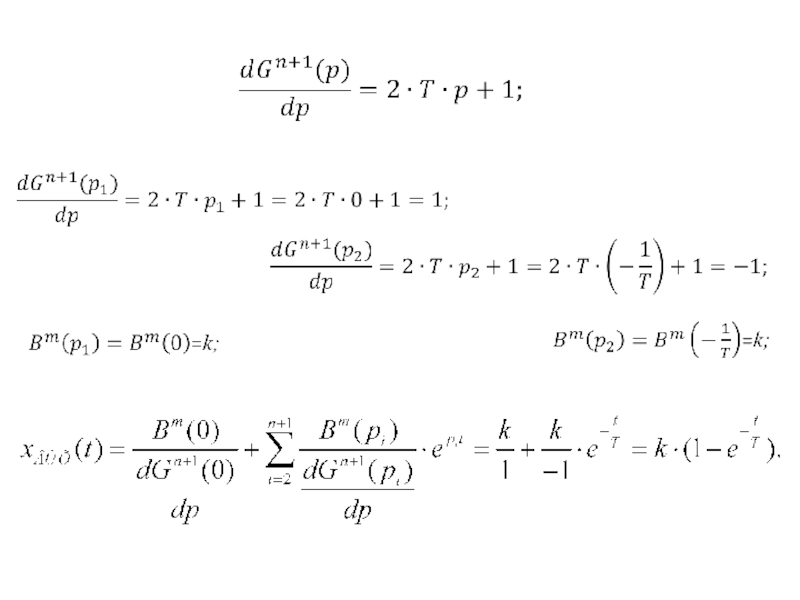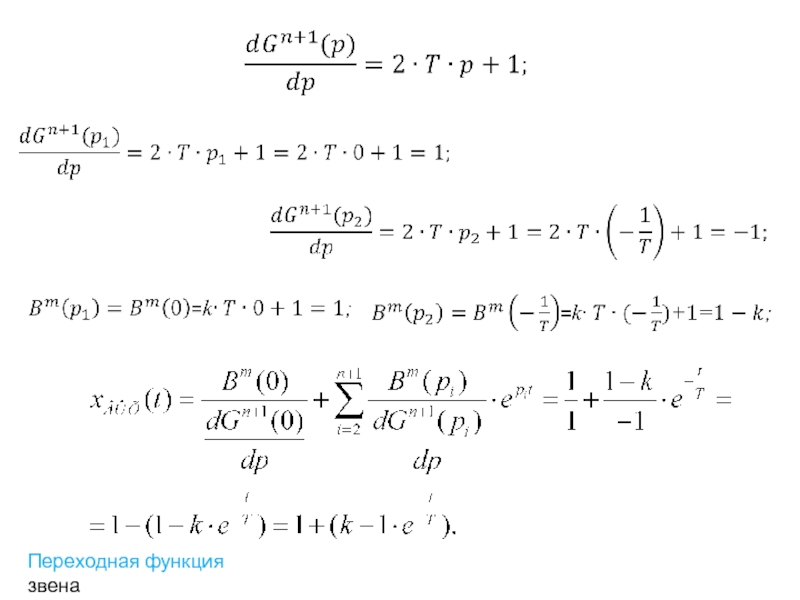- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Типовые динамические звенья ТАУ презентация
Содержание
- 1. Типовые динамические звенья ТАУ
- 2. Характер переходных процессов в
- 3. 1. Элементарные типовые динамические звенья.
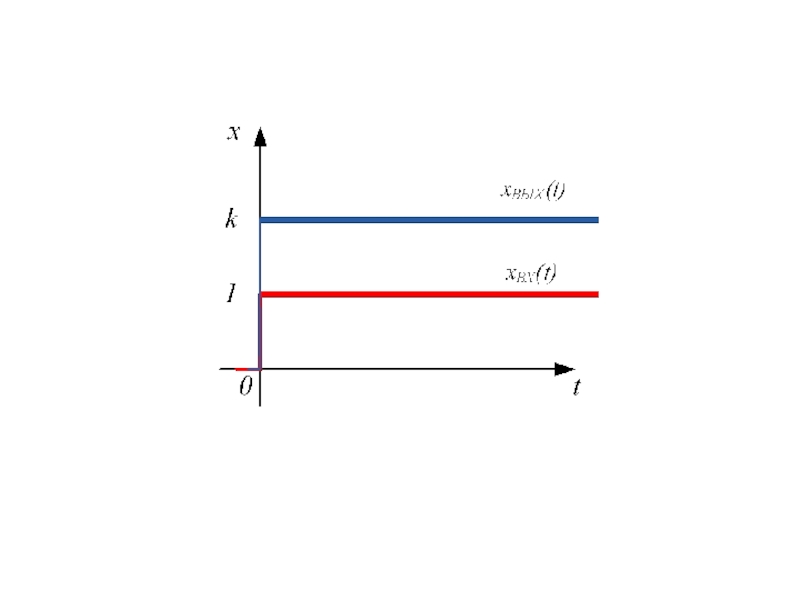
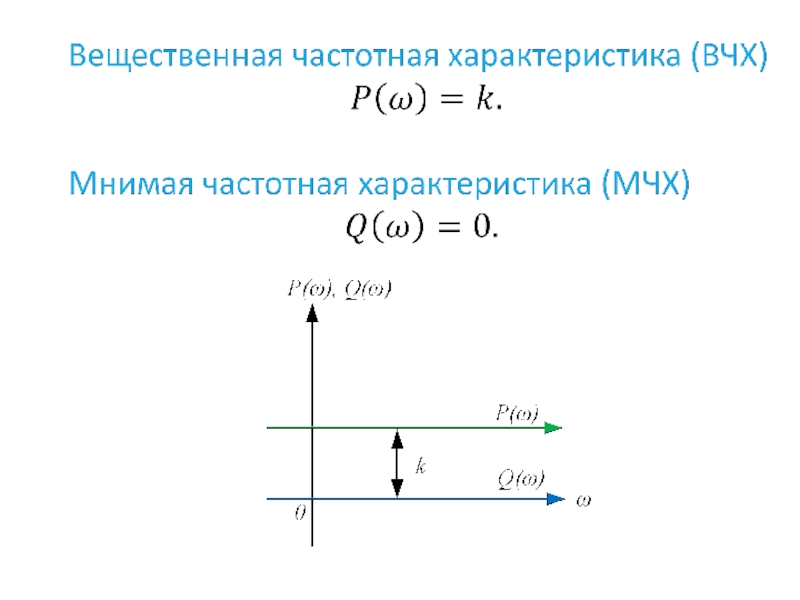
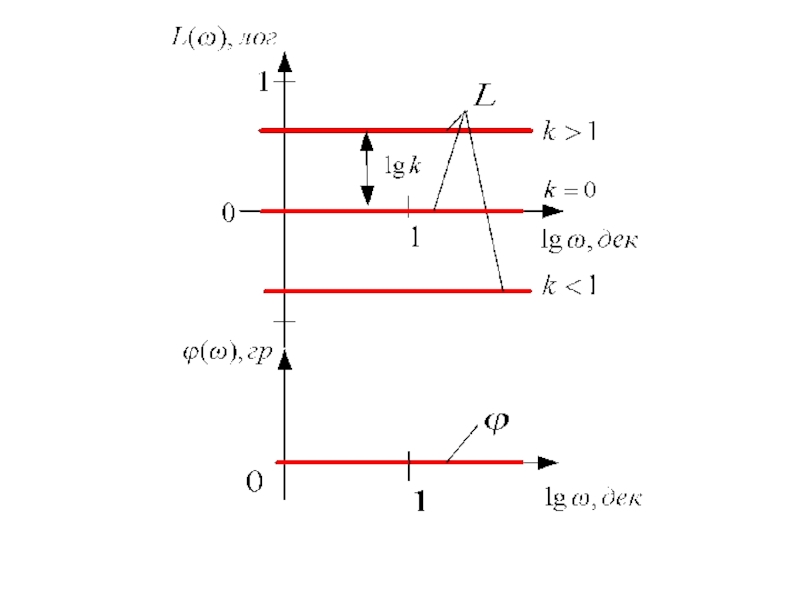
- 4. 1.1 Усилительное (пропорциональное) звено
- 5. Если перейти к операторной форме записи, то
- 6.
- 8.
- 9.
- 10.
- 13. 1.2 Интегрирующее звено Идеальным интегрирующим звеном
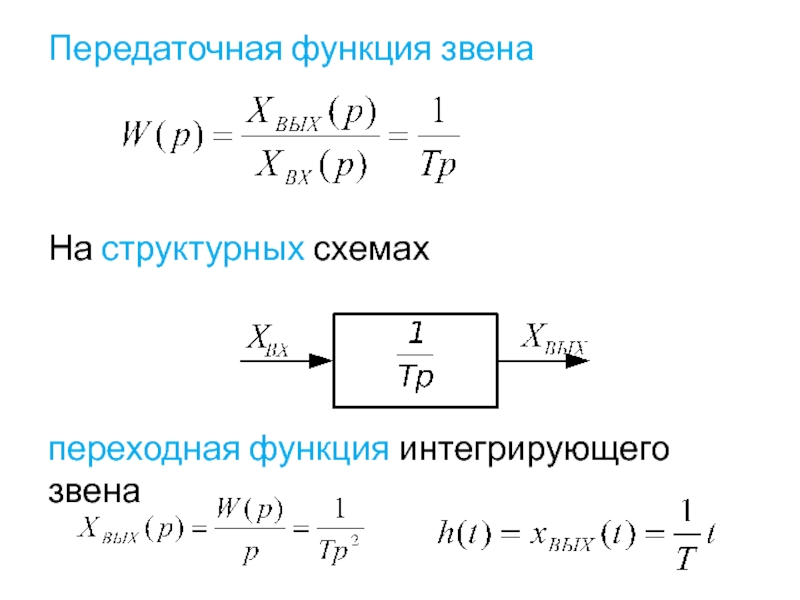
- 14. Передаточная функция звена
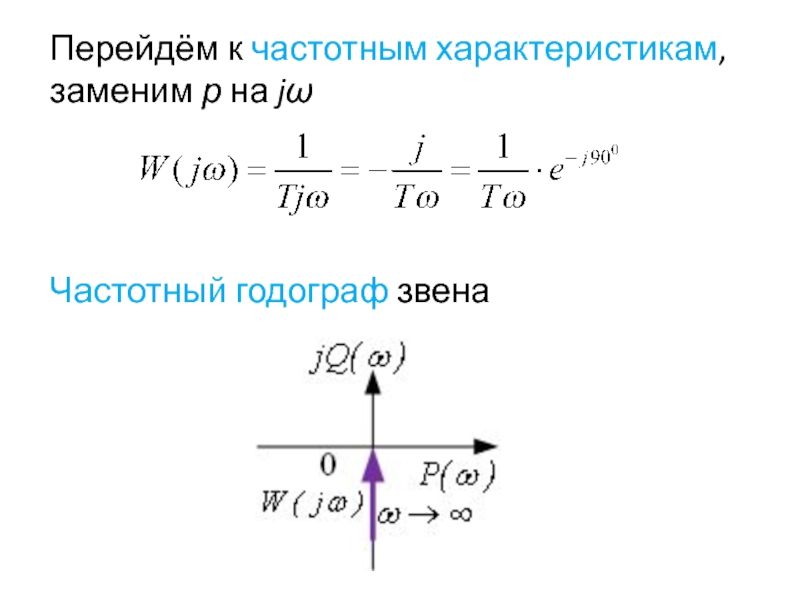
- 16. Перейдём к частотным характеристикам, заменим р на
- 17.
- 18. АЧХ интегрирующего звена Логарифмическая амплитудно-частотная характеристика
- 21. 1.3 Дифференцирующее звено На практике не
- 22. Переходя к изображениям, получим Передаточная
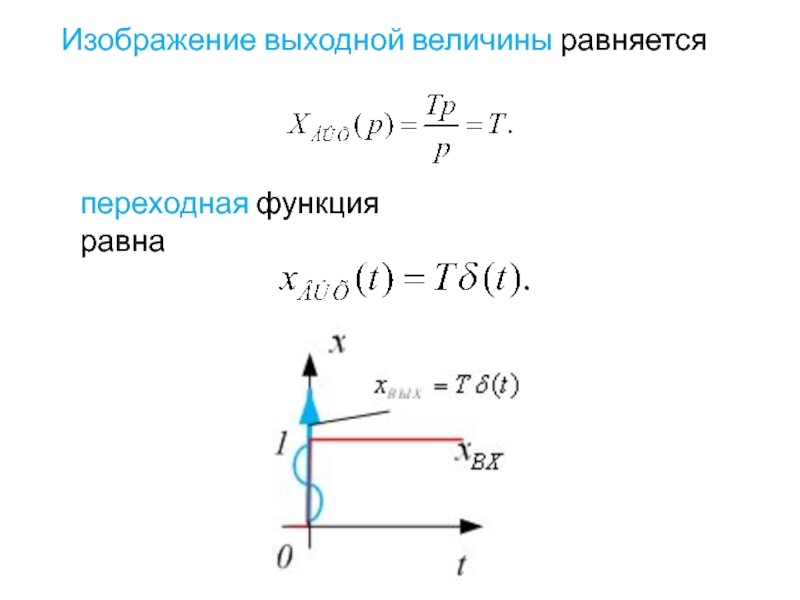
- 23. Изображение выходной величины равняется переходная функция равна
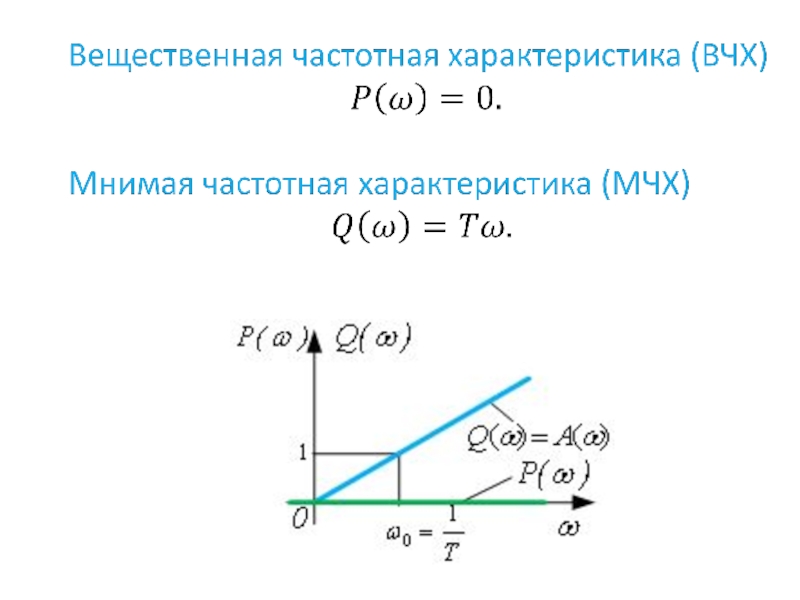
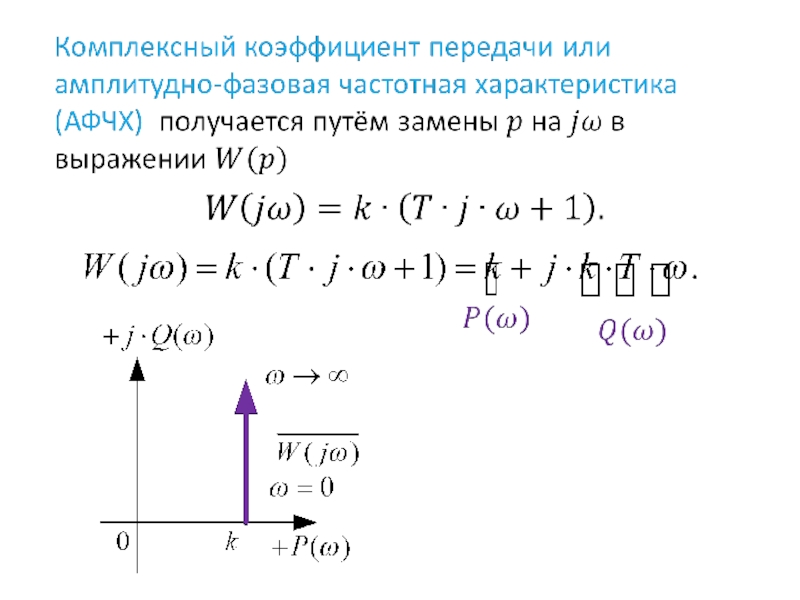
- 24. Перейдём к частотным характеристикам, заменим р на jω. Комплексный коэффициент передачи
- 25.
- 26. АЧХ дифференцирующего звена Логарифмическая амплитудно-частотная характеристика
- 29. 2 Звенья первого порядка 2.1 Инерционное (апериодическое)
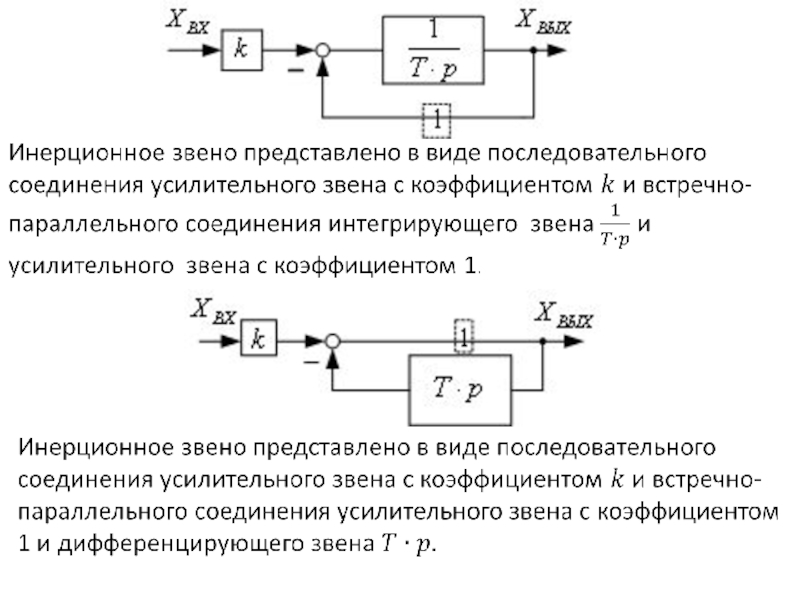
- 30. Применяя преобразование Лапласа при нулевых начальных условиях,
- 31.
- 32. Решение уравнения
- 33.
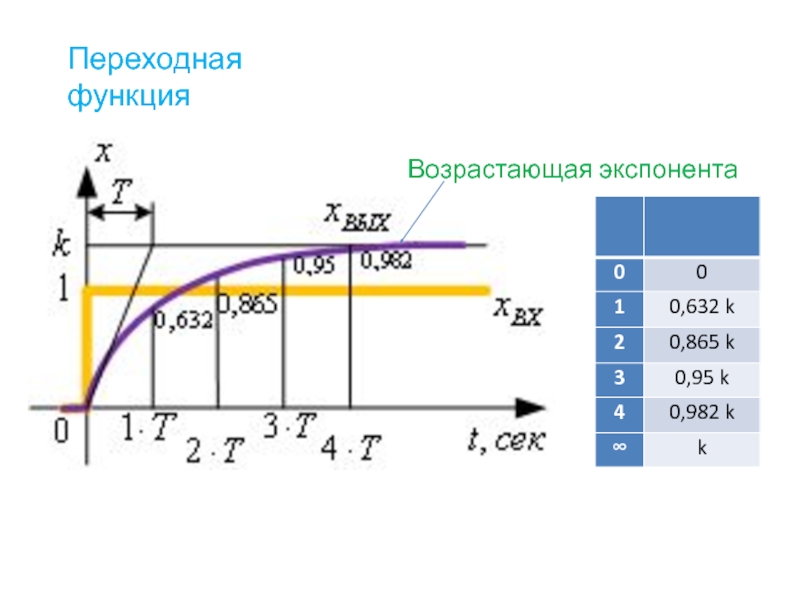
- 34. Переходная функция Возрастающая экспонента
- 35.
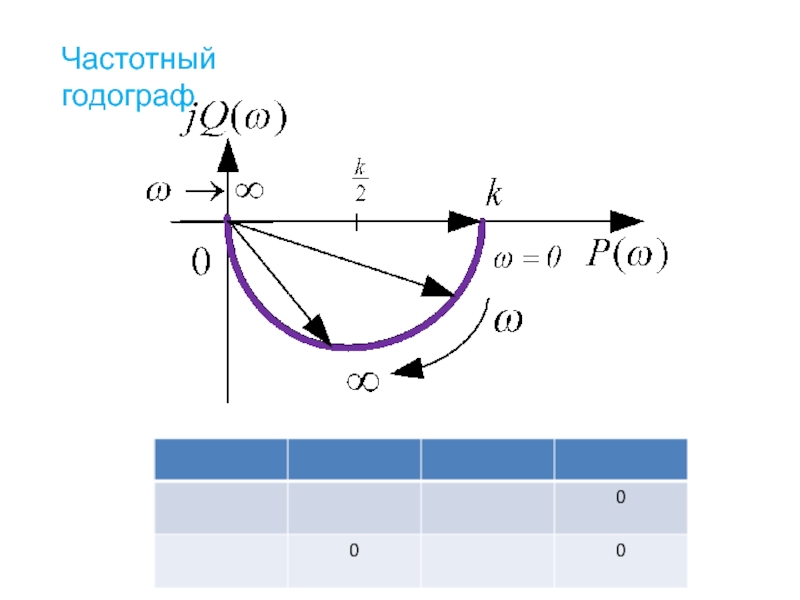
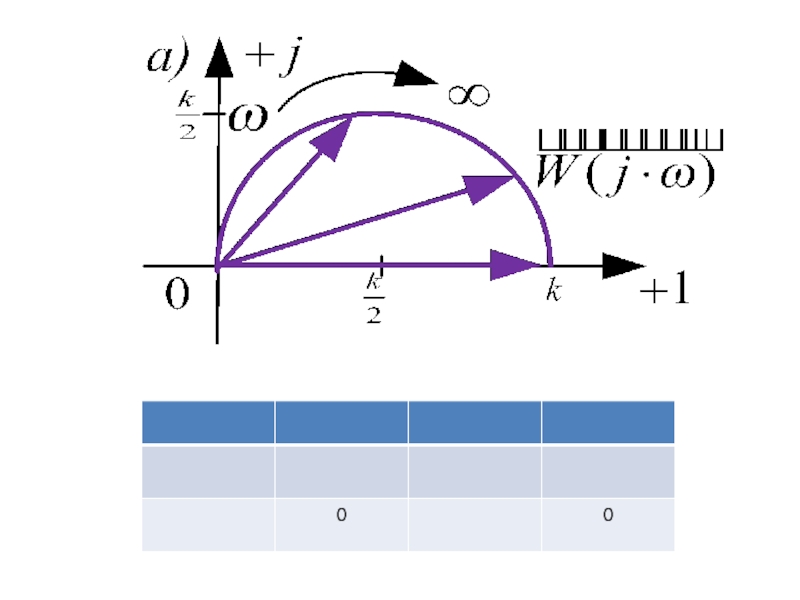
- 36. Частотный годограф
- 37.
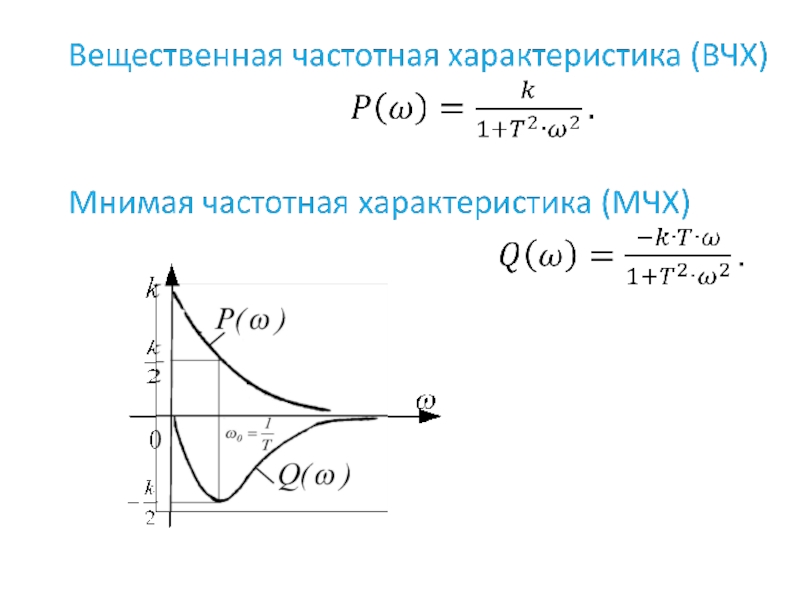
- 38. Амплитудно-частотная характеристика АЧХ инерционного звена Логарифмическая
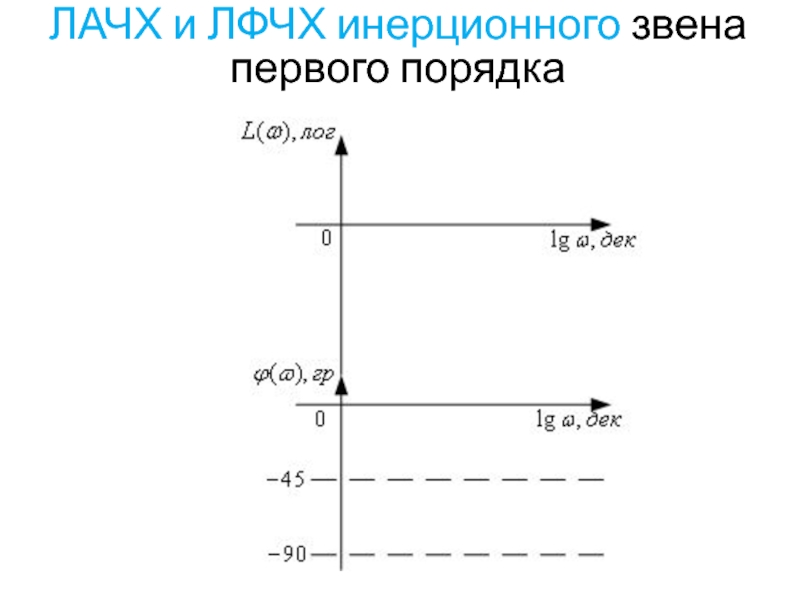
- 39. Логарифмическая фазо-частотная характеристика (ЛФЧХ)
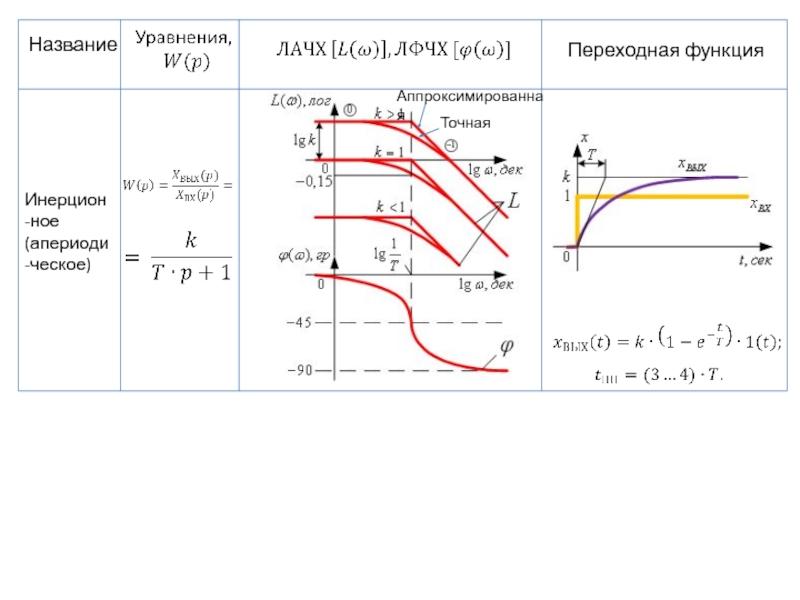
- 40. Логарифмическая амплитудно-частотная характеристика Точное построение L(ω)
- 41. Вторая асимптота характеризует при больших частотах, когда
- 42. ЛАЧХ и ЛФЧХ инерционного звена первого порядка
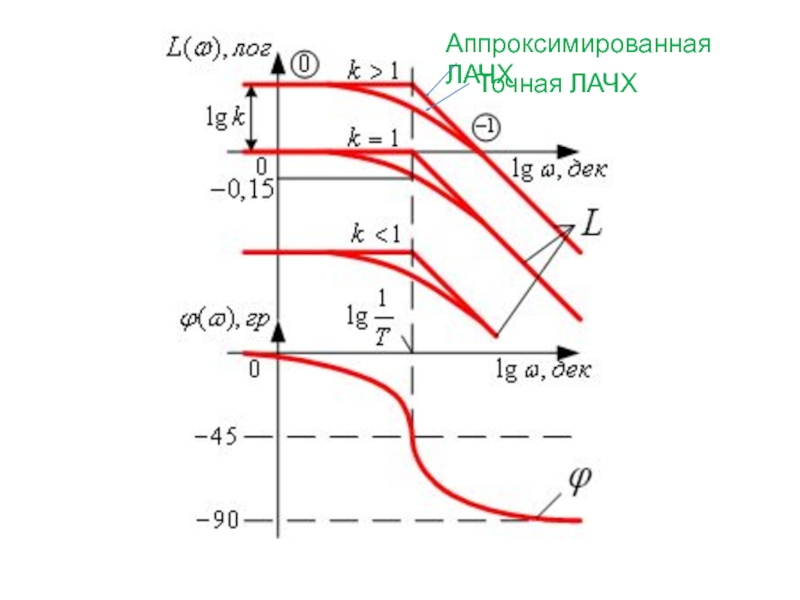
- 43. Аппроксимированная ЛАЧХ Точная ЛАЧХ
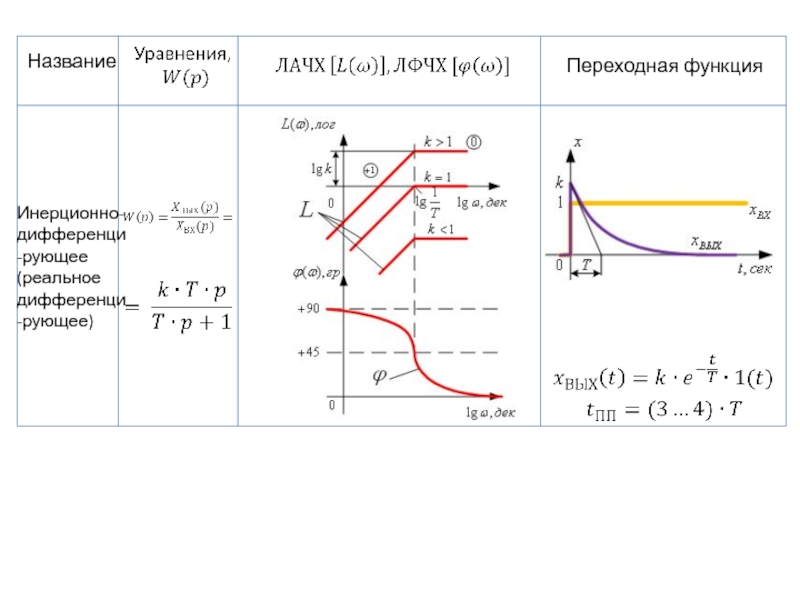
- 44. 2.2 Реальное дифференцирующее звено первого порядка
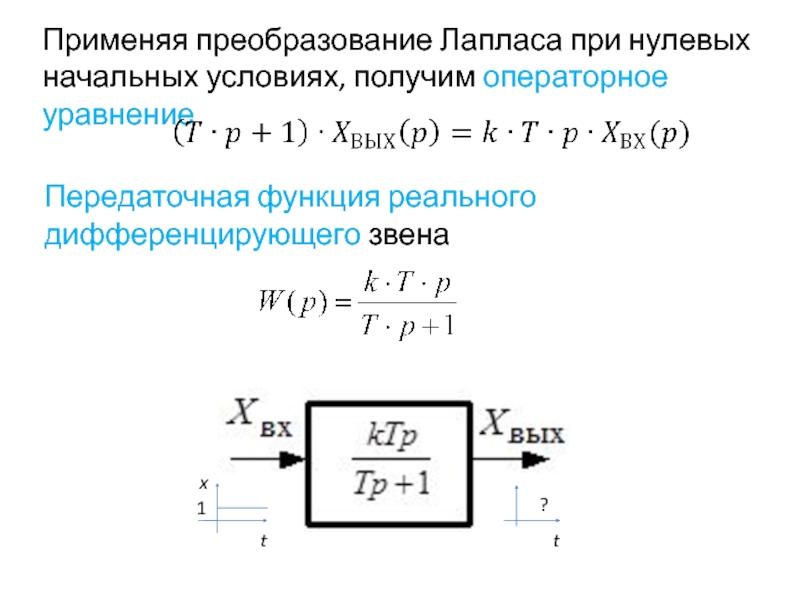
- 45. Применяя преобразование Лапласа при нулевых начальных условиях,
- 47. Решение уравнения
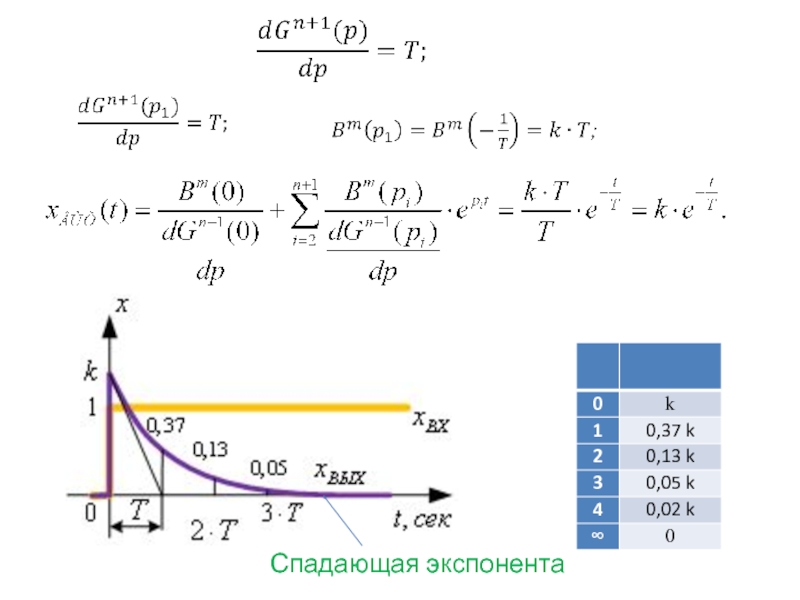
- 48. Спадающая экспонента
- 49.
- 51.
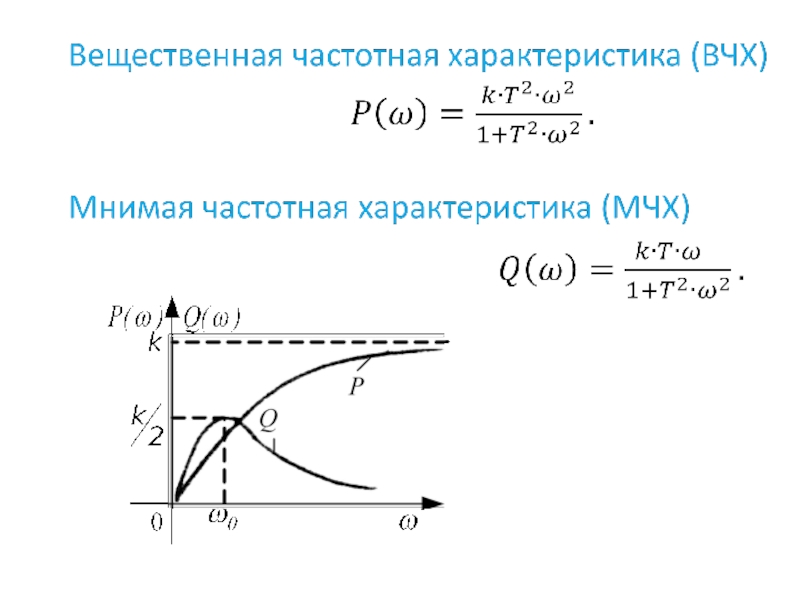
- 52. Амплитудно-частотная характеристика АЧХ реального дифференцирующего звена
- 53. Логарифмическая фазо-частотная характеристика (ЛФЧХ)
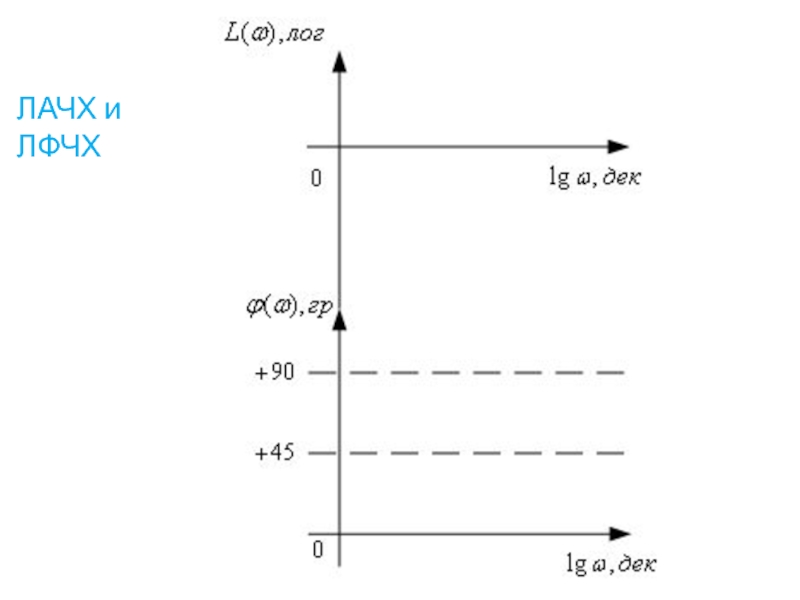
- 54. ЛАЧХ и ЛФЧХ
- 55. ЛАЧХ и ЛФЧХ
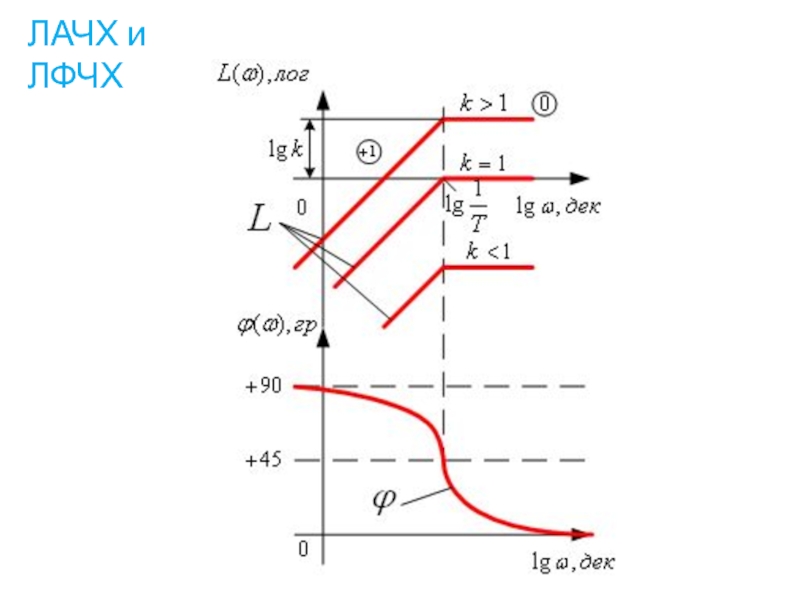
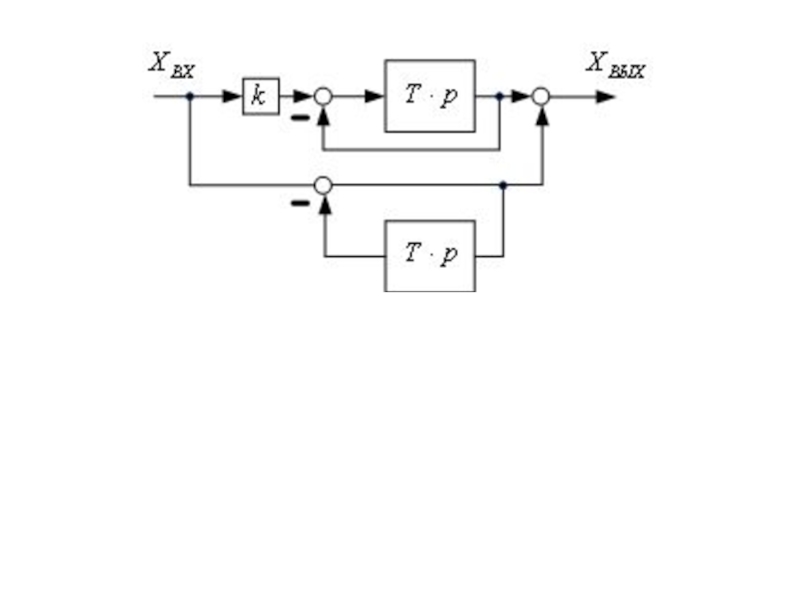
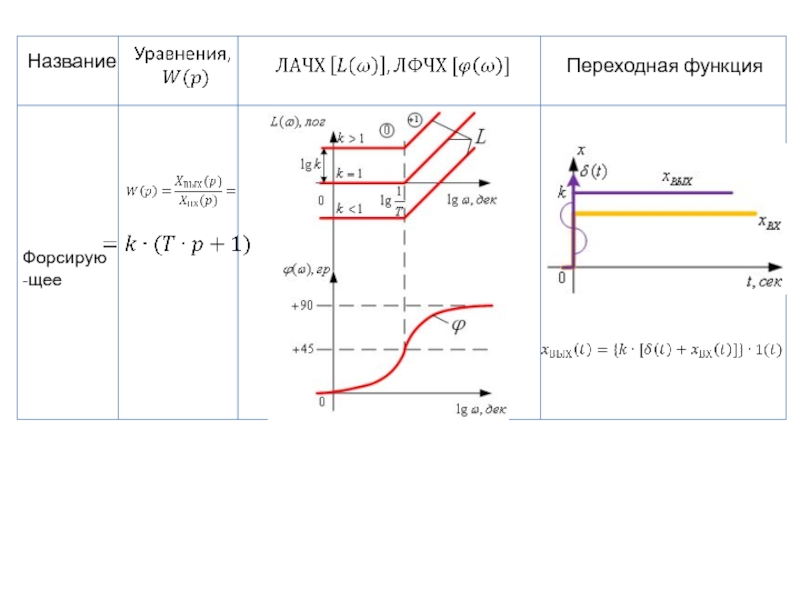
- 56. 2.3 Форсирующее звено 1 – го порядка Передаточная функция форсирующего звена
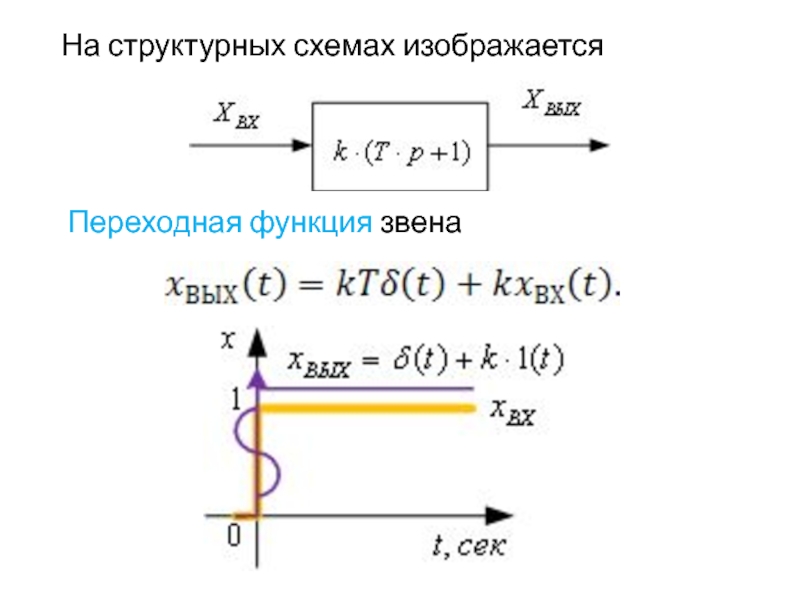
- 57. Переходная функция звена На структурных схемах изображается
- 58.
- 59.
- 60. Амплитудно-частотная характеристика АЧХ инерционного звена Логарифмическая
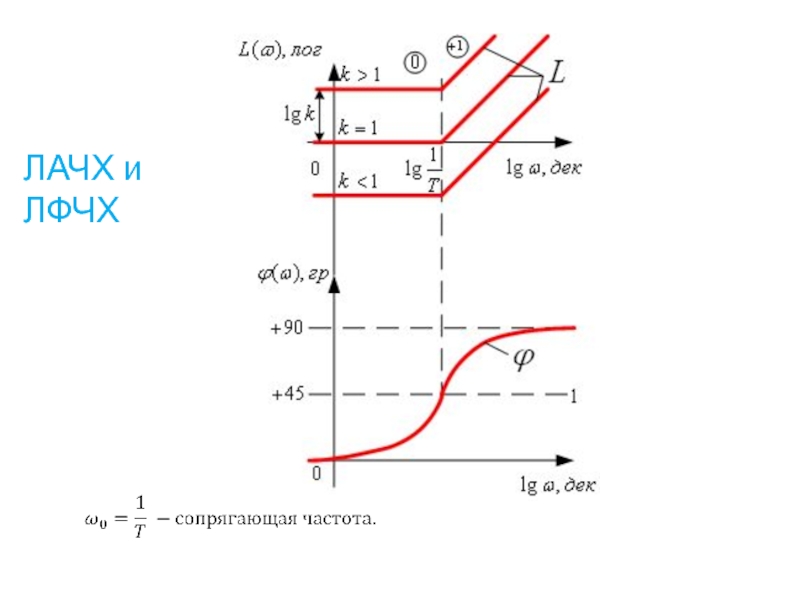
- 61. Логарифмическая фазо-частотная характеристика (ЛФЧХ) ЛАЧХ и ЛФЧХ
- 62. ЛАЧХ и ЛФЧХ
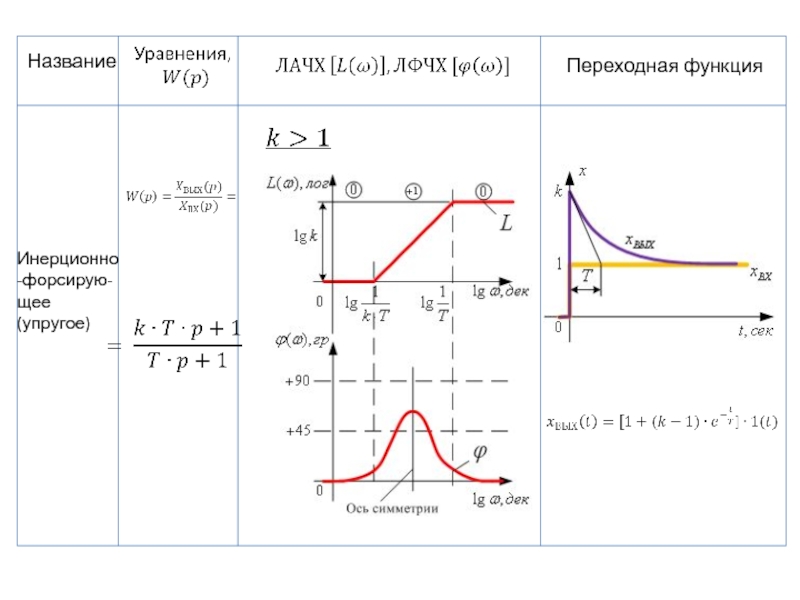
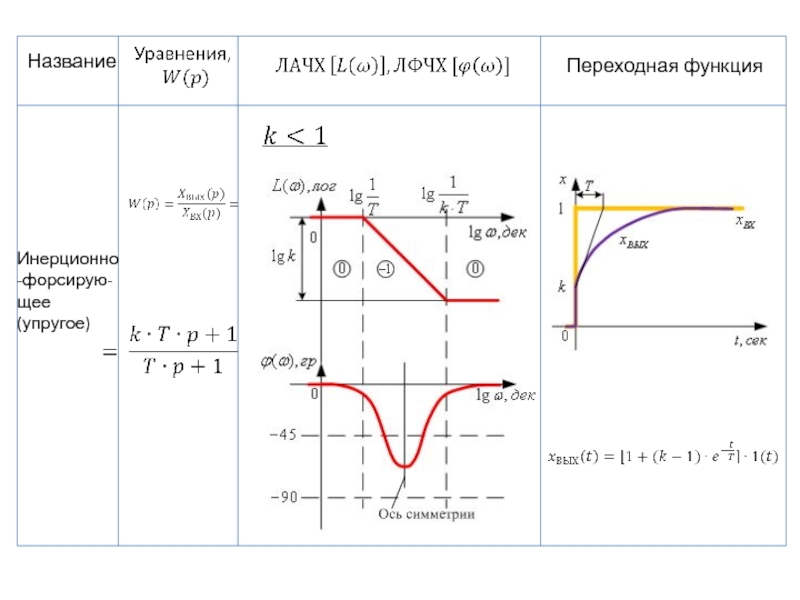
- 63. 2.4 Инерционно-форсирующее (упругое) звено
- 64. Применяя преобразование Лапласа при нулевых начальных условиях,
- 66. Решение уравнения
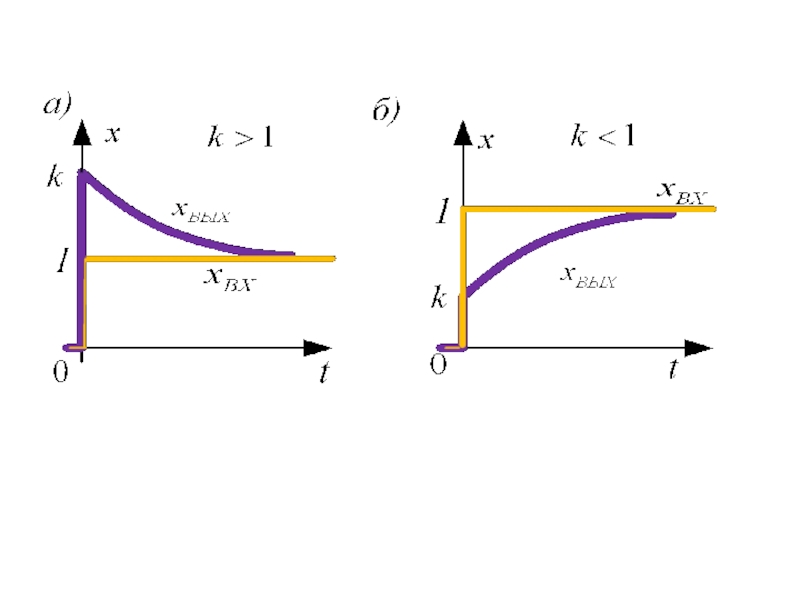
- 67. Переходная функция звена
- 69.
- 70.
- 71.
- 72. Амплитудно-частотная характеристика АЧХ упругого звена Логарифмическая
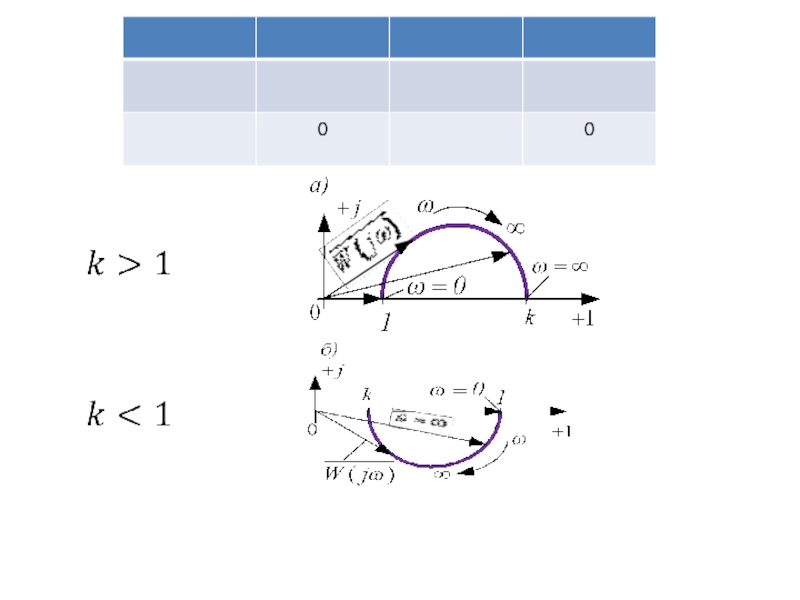
- 73. Логарифмическая амплитудно-фазовая характеристика описывается уравнением Асимптотические
- 74. ЛАЧХ и ЛФЧХ
- 75. Звенья второго порядка Звеном второго порядка называется
- 76. В зависимости от вида корней характеристического уравнения
- 77. В случае вещественных корней апериодическое звено второго
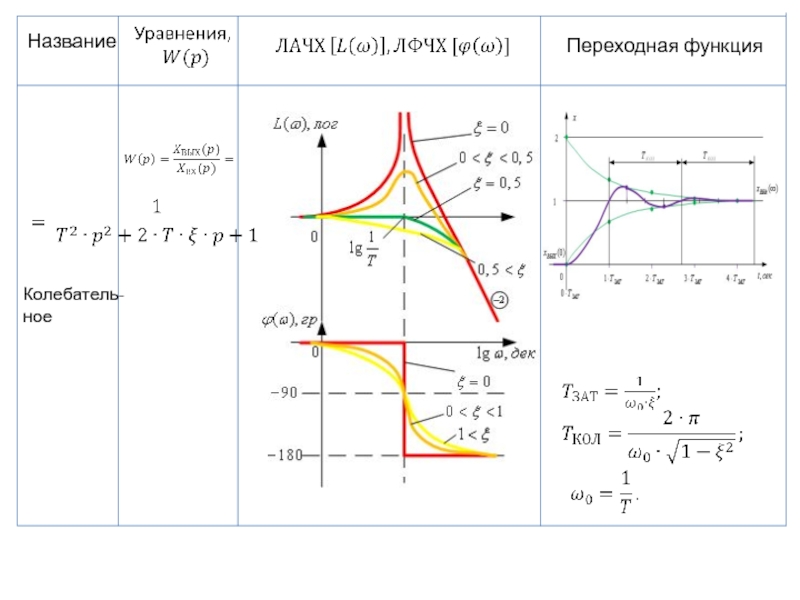
- 78. Колебательное звено Если корни уравнения будут комплексными, то инерционное звено второго порядка станет колебательным (ξ
- 79. Передаточная функция инерционного звена 2 порядка Амплитудно-фазовая характеристика
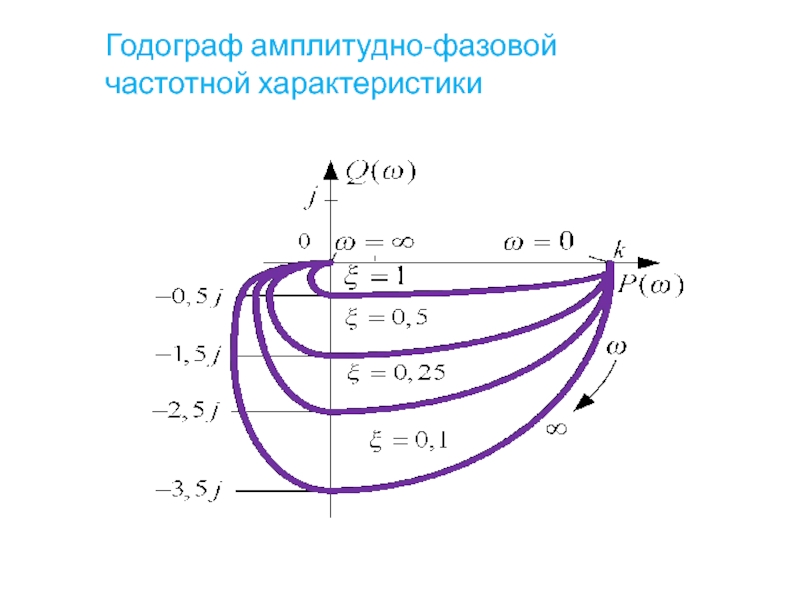
- 80. Годограф амплитудно-фазовой частотной характеристики
- 81. Амплитудно-частотная и фазо-частотная характеристики колебательного звена выражаются
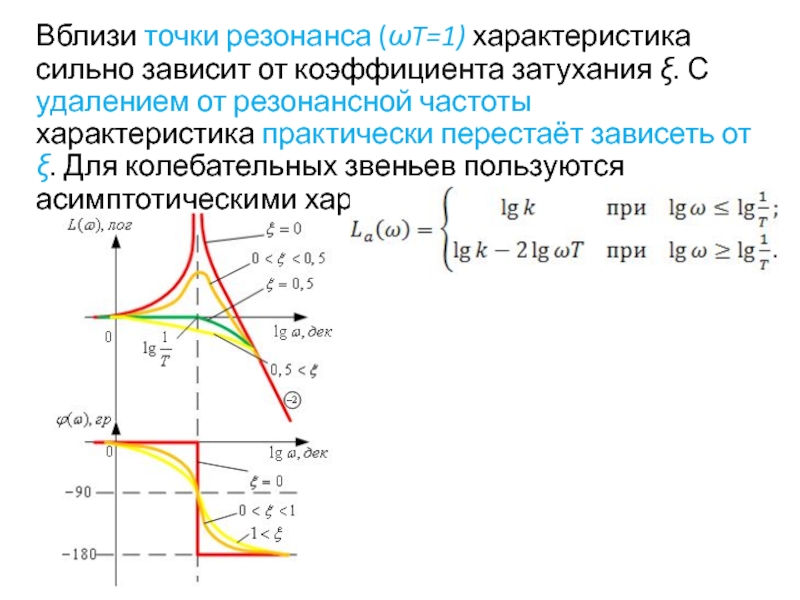
- 82. Вблизи точки резонанса (ωT=1) характеристика сильно зависит
- 83. Общее свойство минимально-фазовых устойчивых звеньев Общим показателем
- 84. Рассмотрим сомножитель числителя jω-qi. Эта разность представляет
- 85. Для минимально-фазовой системы определение приближённого значения фазы
- 91. 1. Элементарные типовые динамические звенья
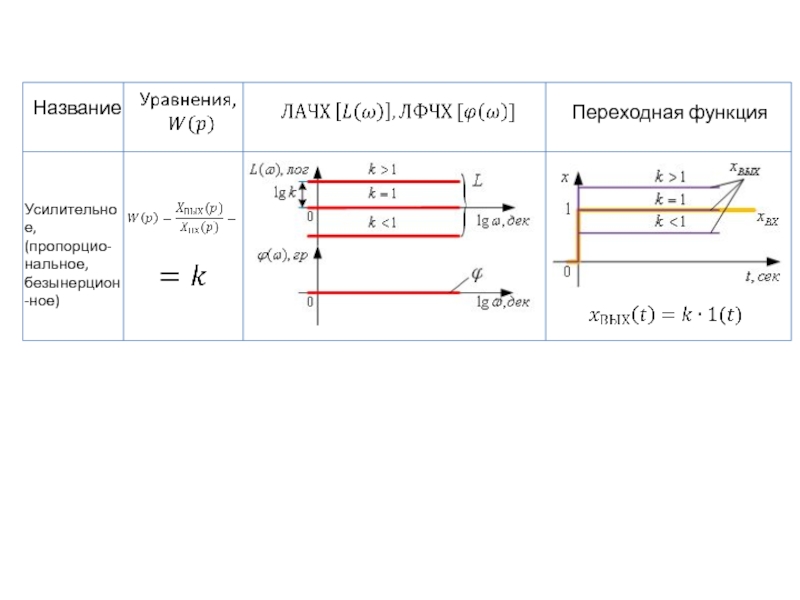
- 92. Название Переходная функция Усилительное, (пропорцио-
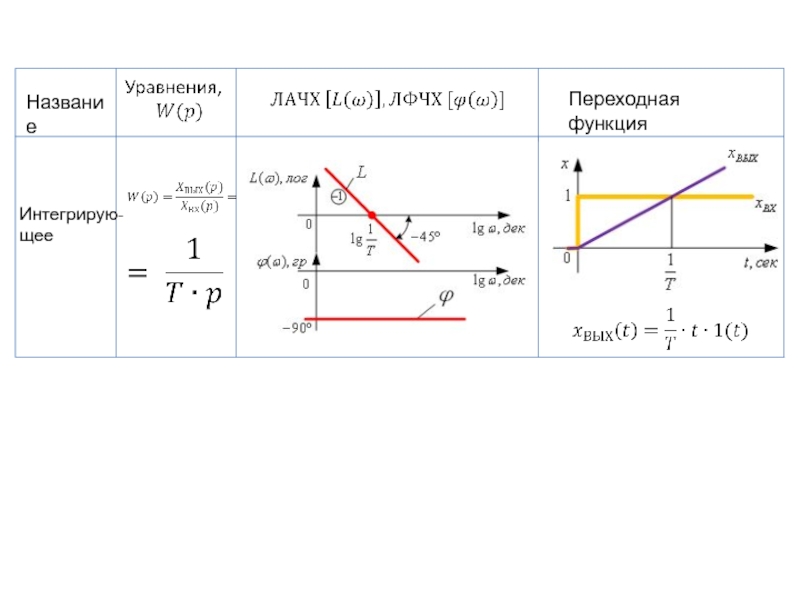
- 93. Интегрирую- щее Название Переходная функция
- 94. Название Переходная функция Дифферен-цирующее
- 95. 2. Реальные типовые динамические звенья 2.1 Звенья первого порядка
- 96. Название Переходная функция Инерцион-ное (апериоди-ческое) Аппроксимированная Точная
- 97. Название Переходная функция Инерционно-дифференци-рующее (реальное дифференци-рующее)
- 98. Название Переходная функция Форсирую-щее
- 99. Название Переходная функция Инерционно-форсирую-щее (упругое)
- 100. Название Переходная функция Инерционно-форсирую-щее (упругое)
- 101. 2. Реальные типовые динамические звенья 2.2 Звенья второго порядка
- 102. Название Переходная функция Колебатель-ное
Характер переходных процессов в САУ зависит от динамических свойств элементов, из которых она состоит. Эти элементы могут быть самыми разнообразными по назначению, конструктивному исполнению, принципу работы и т.д.
Слайд 2 Характер переходных процессов в САУ зависит от динамических
свойств элементов, из которых она состоит. Эти элементы могут быть самыми разнообразными по назначению, конструктивному исполнению, принципу работы и т.д. Однако, независимо от назначения и конструктивного исполнения, все элементы САУ могут быть подразделены на небольшое число звеньев, обладающих определенными динамическими свойствами, т.е. описываемых определенными дифференциальными уравнениями. Такие звенья носят название типовых динамических звеньев.
Различают две группы типовых звеньев: элементарные динамические звенья и
реальные типовые динамические звенья, представляющие собой соединения из элементарных звеньев.
Различают две группы типовых звеньев: элементарные динамические звенья и
реальные типовые динамические звенья, представляющие собой соединения из элементарных звеньев.
Слайд 31. Элементарные типовые динамические звенья.
- Усилительное (пропорциональное) звено.
- Интегрирующее звено.
- Дифференцирующее звено.
2. Реальные типовые динамические звенья.
Звенья первого порядка, основными из них являются.
- Инерционное звено.
- Реальное дифференцирующее (инерционно- дифференцирующее).
- Форсирующее звено.
- Инерционно-форсирующее (упругое) звено.
Звенья второго порядка.
- Колебательное звено.
- Консервативное звено.
- Дифференцирующее звено.
2. Реальные типовые динамические звенья.
Звенья первого порядка, основными из них являются.
- Инерционное звено.
- Реальное дифференцирующее (инерционно- дифференцирующее).
- Форсирующее звено.
- Инерционно-форсирующее (упругое) звено.
Звенья второго порядка.
- Колебательное звено.
- Консервативное звено.
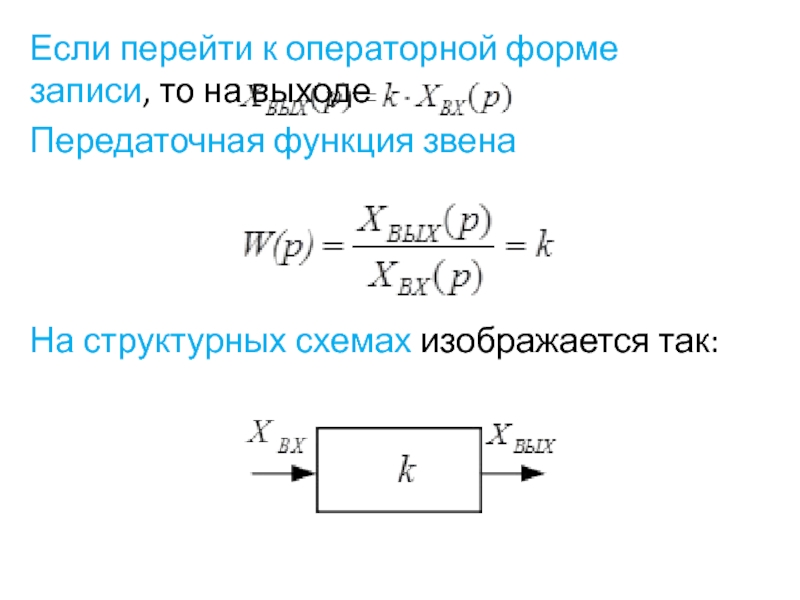
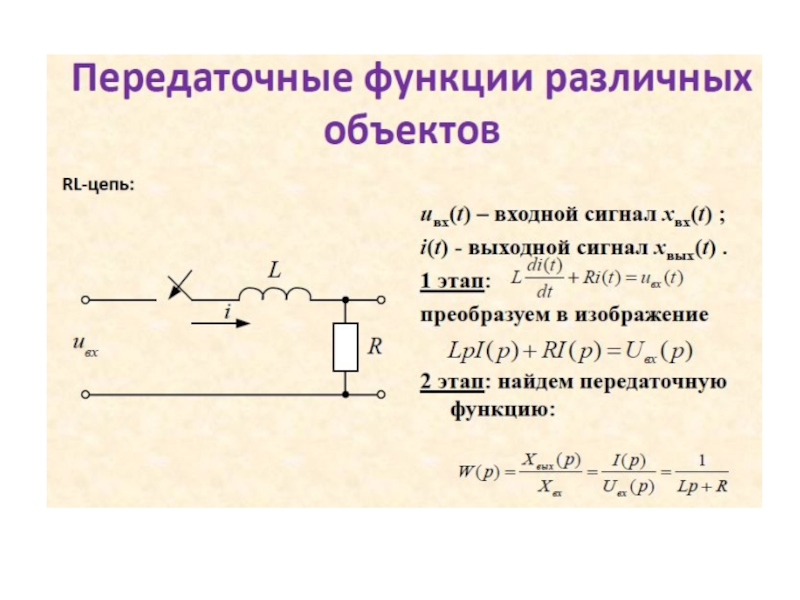
Слайд 5Если перейти к операторной форме записи, то на выходе
Передаточная функция звена
На структурных схемах изображается так:
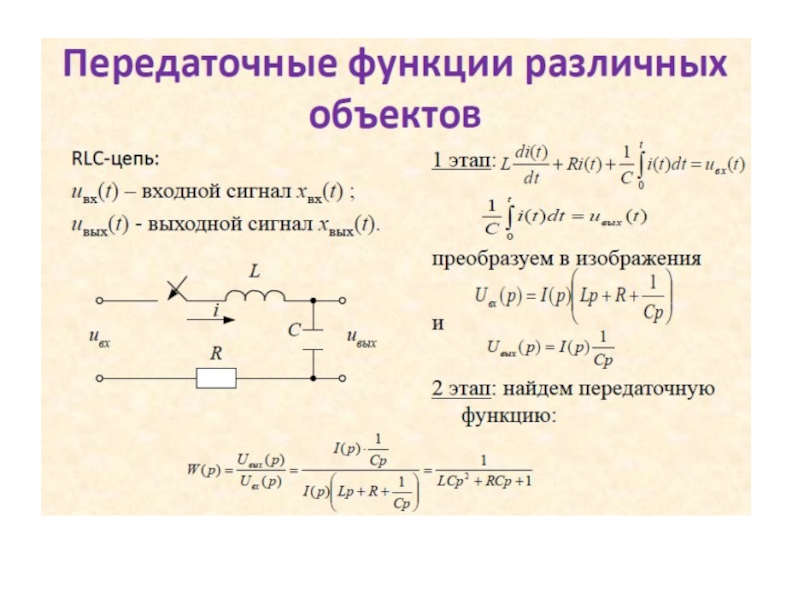
Слайд 131.2 Интегрирующее звено
Идеальным интегрирующим звеном называется звено, выходная величина которого
пропорциональна интегралу входной величины
,
где Т – постоянная времени.
Такие звенья называются интегрирующими. Примерами реальных элементов, эквивалентные схемы, которых сводятся к интегрирующему звену являются электрический конденсатор, вращающийся вал, гидравлический резервуар, гидравлический усилитель и др. Переходя к изображениям, получим
,
где Т – постоянная времени.
Такие звенья называются интегрирующими. Примерами реальных элементов, эквивалентные схемы, которых сводятся к интегрирующему звену являются электрический конденсатор, вращающийся вал, гидравлический резервуар, гидравлический усилитель и др. Переходя к изображениям, получим
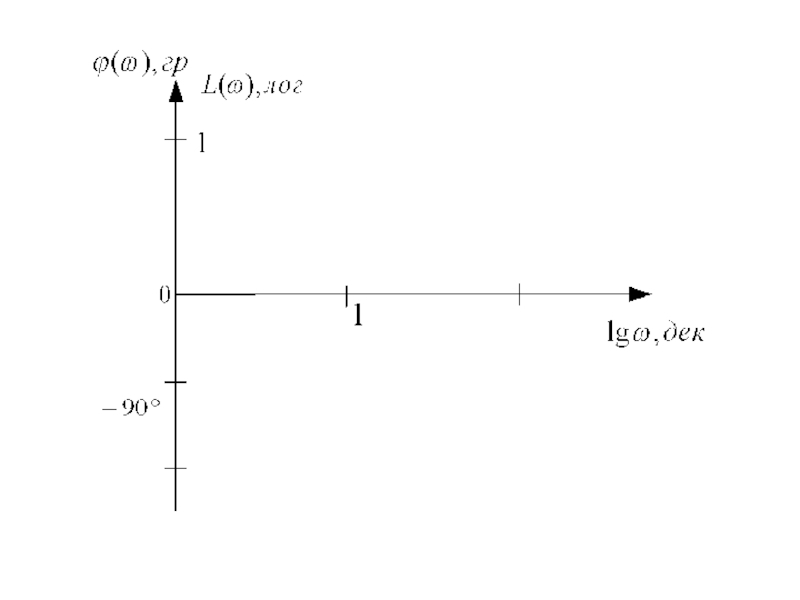
Слайд 18АЧХ интегрирующего звена
Логарифмическая амплитудно-частотная характеристика (ЛАЧХ)
в функции lgω имеет вид прямой с наклоном -1 лог/дек.
Логарифмическая фазо-частотная характеристика (ЛФЧХ)
Слайд 211.3 Дифференцирующее звено
На практике не существует реального элементе, в котором
на выходе точно воспроизводилась бы производная от любого входного сигнала. Однако, составляя структурную схему системы, её можно так разделить на звенья, что введение понятия дифференцирующего звена будет вполне обосновано. В этом случае выходная величина хВЫХ(t) зависит от входной величины хВХ(t) как производная (идеальное дифференцирующее звено)
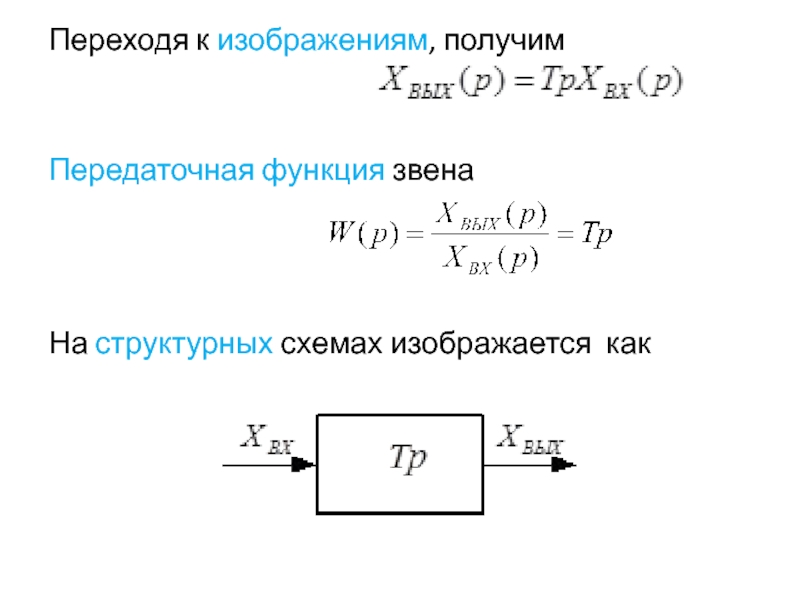
Слайд 22Переходя к изображениям, получим
Передаточная функция звена
На структурных схемах изображается как
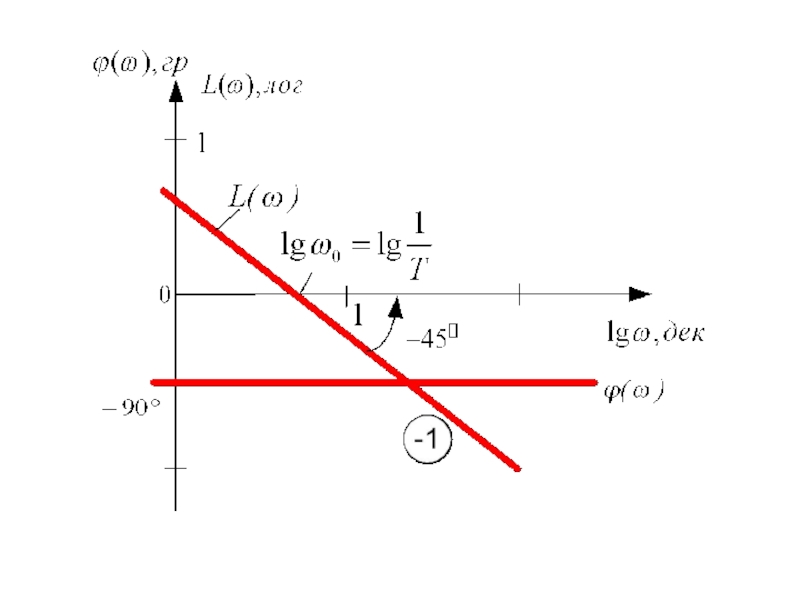
Слайд 26АЧХ дифференцирующего звена
Логарифмическая амплитудно-частотная характеристика (ЛАЧХ)
в функции lgω имеет вид прямой с наклоном +1 лог/дек.
Логарифмическая фазо-частотная характеристика (ЛФЧХ)
Слайд 292 Звенья первого порядка
2.1 Инерционное (апериодическое) звено
Инерционным (апериодическим)
звеном 1 – го порядка называется такое звено, связь между выходом и входом определяется линейным заданным уравнением первого порядка вида
где Т – постоянная времени инерционного звена, обусловленная наличием массы, момента инерции, индуктивности, ёмкости и т.д.;
k – коэффициент усиления (или передачи).
где Т – постоянная времени инерционного звена, обусловленная наличием массы, момента инерции, индуктивности, ёмкости и т.д.;
k – коэффициент усиления (или передачи).
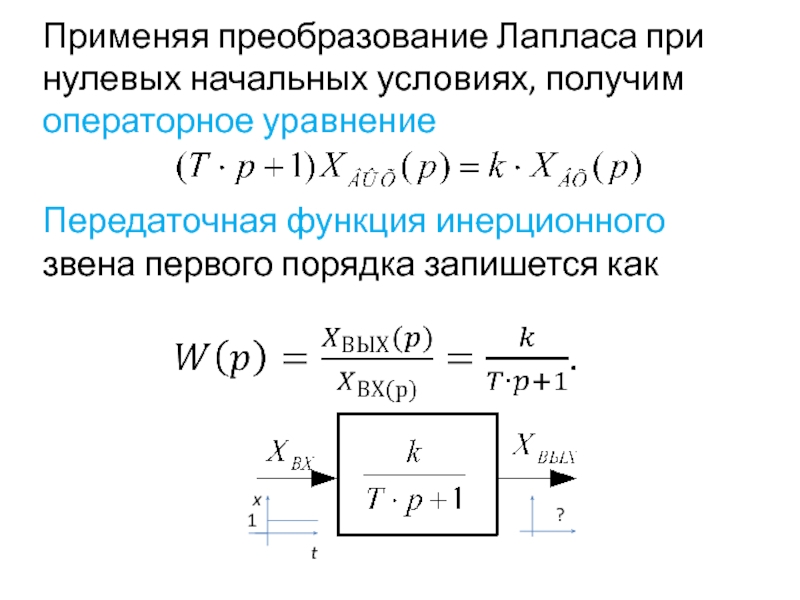
Слайд 30Применяя преобразование Лапласа при нулевых начальных условиях, получим операторное уравнение
Передаточная функция инерционного звена первого порядка запишется как
x
1
t
?
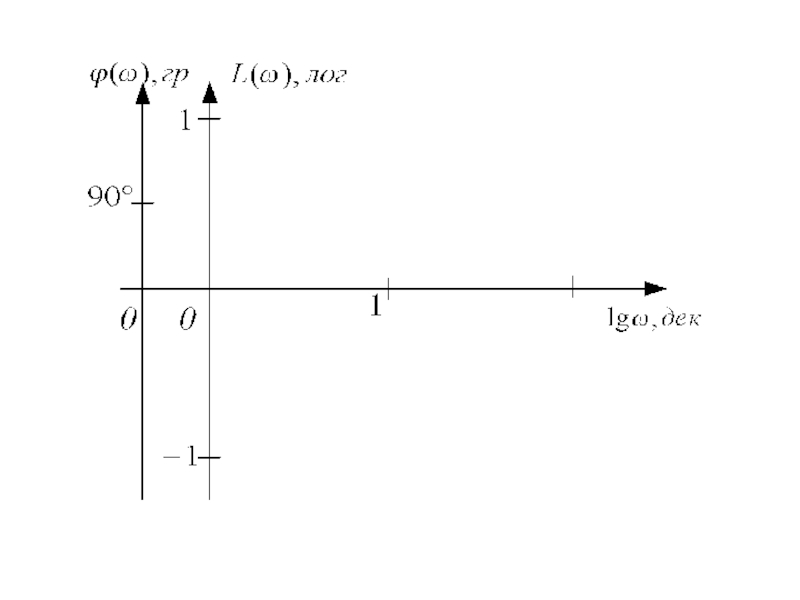
Слайд 38Амплитудно-частотная характеристика АЧХ
инерционного звена
Логарифмическая амплитудно-частотная характеристика (ЛАЧХ)
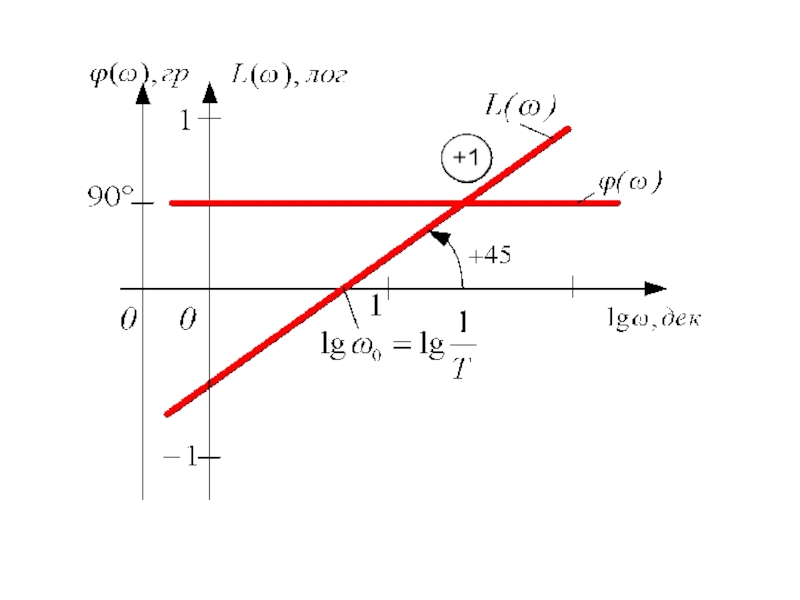
Слайд 40Логарифмическая амплитудно-частотная характеристика
Точное построение L(ω) заключается в последовательном определении значений
L(ω) при различных частотах ω. Построение ЛАХ обычно упрощают, заменяя точную L’(ω) асимптотами. Первая асимптота характеризует при малых частотах, когда величиной ω2Т2 можно пренебречь, т.е. принимают
Слайд 41Вторая асимптота характеризует при больших частотах, когда ω2Т2 »1, т.е. принимают
Эта асимптота зависит от частоты. Если принять приращение частоты на одну декаду (ω2=10 ω1), то амплитуда изменится на величину
Точка сопряжения обеих асимптот
Величина ω0 определяется постоянной времени инерционного звена первого порядка и называется сопрягающей частотой.
Слайд 45Применяя преобразование Лапласа при нулевых начальных условиях, получим операторное уравнение
Передаточная функция
реального дифференцирующего звена
x
1
t
?
t
Слайд 52Амплитудно-частотная характеристика АЧХ
реального дифференцирующего звена
Логарифмическая амплитудно-частотная характеристика (ЛАЧХ)
Слайд 60Амплитудно-частотная характеристика АЧХ
инерционного звена
Логарифмическая амплитудно-частотная характеристика (ЛАЧХ)
Слайд 64Применяя преобразование Лапласа при нулевых начальных условиях, получим операторное уравнение
Передаточная функция
упругого звена
На структурных схемах изображается
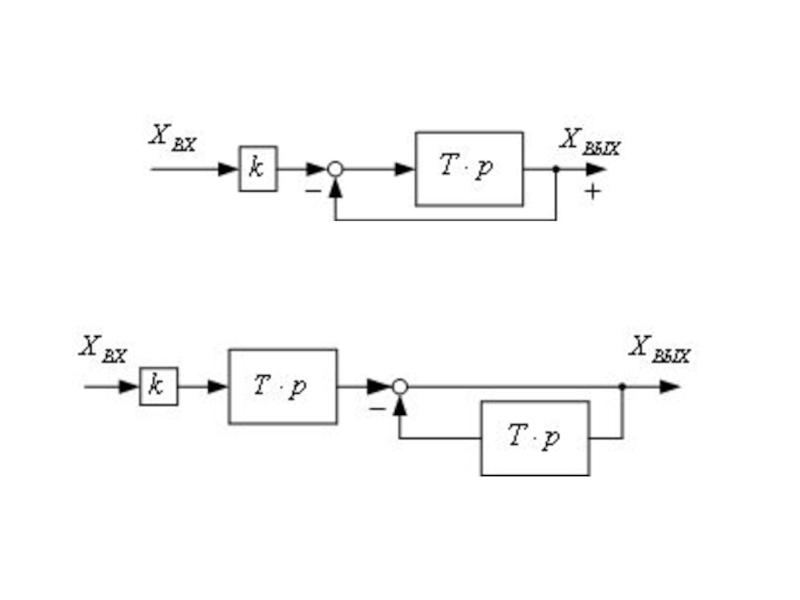
На структурных схемах изображается
x
1
t
?
t
Слайд 72Амплитудно-частотная характеристика АЧХ
упругого звена
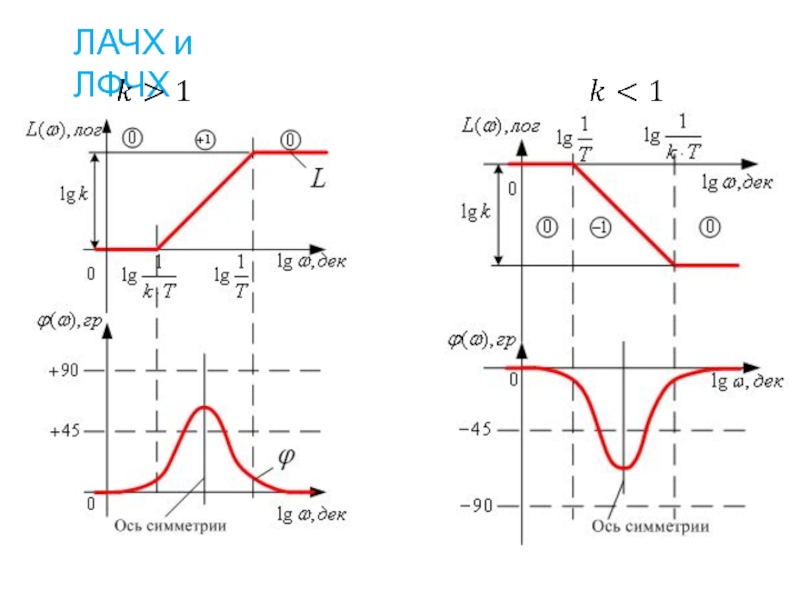
Логарифмическая амплитудно-частотная характеристика (ЛАЧХ)
Логарифмическая фазо-частотная характеристика (ЛАЧХ)
Слайд 73Логарифмическая амплитудно-фазовая характеристика описывается уравнением
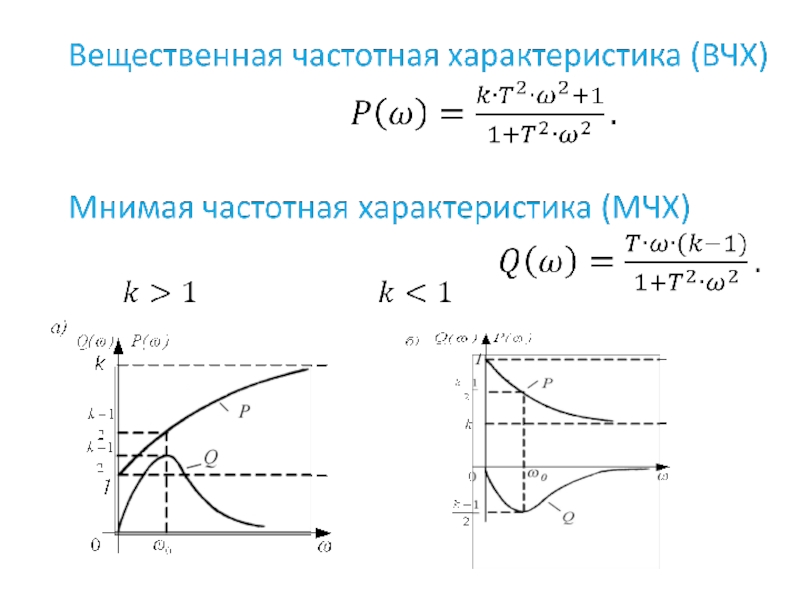
Асимптотические характеристики в зависимости от величины k
выражаются различно:
Слайд 75Звенья второго порядка
Звеном второго порядка называется звено, связь между выходной и
входной величиной которого определяется линейным дифференциальным уравнением второго порядка вида
,
где Т – постоянная времени ; ξ – относительный коэффициент затухания (демпфирования).
Применяя преобразование Лапласа при нулевых начальных условиях, получим операторное уравнение
,
где Т – постоянная времени ; ξ – относительный коэффициент затухания (демпфирования).
Применяя преобразование Лапласа при нулевых начальных условиях, получим операторное уравнение
Слайд 76В зависимости от вида корней характеристического уравнения инерционное звено второго порядка
может иметь различные переходные характеристики. Это позволяет установить три разновидности звена – апериодическое, колебательное и консервативное.
При единичном входном воздействии для случая вещественных различных корней р1 и р2 получим переходную функцию (ξ≥1):
При единичном входном воздействии для случая вещественных различных корней р1 и р2 получим переходную функцию (ξ≥1):
Слайд 77В случае вещественных корней апериодическое звено второго порядка эквивалентно последовательному соединению
двух инерционных звеньев первого порядка, поэтому передаточная функция может быть записана в виде
По выражению W(p) после замены р на jω получим частотную функцию W(jω) апериодического звена второго порядка, которая определяет частотные характеристики звена.
По выражению W(p) после замены р на jω получим частотную функцию W(jω) апериодического звена второго порядка, которая определяет частотные характеристики звена.
Слайд 78Колебательное звено
Если корни уравнения будут комплексными, то инерционное звено второго порядка
станет колебательным (ξ<1).
Слайд 81Амплитудно-частотная и фазо-частотная характеристики колебательного звена выражаются уравнениями
Логарифмическая амплитудно-фазовая характеристика колебательного
звена описывается уравнением
Слайд 82Вблизи точки резонанса (ωT=1) характеристика сильно зависит от коэффициента затухания ξ.
С удалением от резонансной частоты характеристика практически перестаёт зависеть от ξ. Для колебательных звеньев пользуются асимптотическими характеристиками
Слайд 83Общее свойство минимально-фазовых устойчивых звеньев
Общим показателем свойств звена является принадлежность нулей
передаточной функции к левой полуплоскости. Представляя передаточную функцию в комплексной форме, комплексный коэффициент передачи можно выразить как
Слайд 84Рассмотрим сомножитель числителя jω-qi. Эта разность представляет собой вектор, начало которого
лежит в точке qi, а конец на мнимой оси в точке jω. Фаза этого вектора характеризует поворот его относительно вещественной оси против часовой стрелки.
На рисунке построены два таких вектора для различных положений точки qi, обозначенных qi' и qi''. Из построения видно, что при одном и том же значении модуля комплекса jω-qi его фаза φ меньше в том случае, когда qi лежит в левой полуплоскости. Поэтому звенья, все нули передаточной функции лежат в левой полуплоскости (Re qi<0), называются минимально-фазовыми. Звенья, передаточные функции которых имеют хотя бы один нуль, лежащий в правой полуплоскости (Re qi.>0), называются неминимально-фазовыми.
На рисунке построены два таких вектора для различных положений точки qi, обозначенных qi' и qi''. Из построения видно, что при одном и том же значении модуля комплекса jω-qi его фаза φ меньше в том случае, когда qi лежит в левой полуплоскости. Поэтому звенья, все нули передаточной функции лежат в левой полуплоскости (Re qi<0), называются минимально-фазовыми. Звенья, передаточные функции которых имеют хотя бы один нуль, лежащий в правой полуплоскости (Re qi.>0), называются неминимально-фазовыми.
Слайд 85Для минимально-фазовой системы определение приближённого значения фазы φi(ωi) можно проводить непосредственно
по среднему наклону ЛАЧХ в частоте ωi без построения ЛФЧХ. При этом
