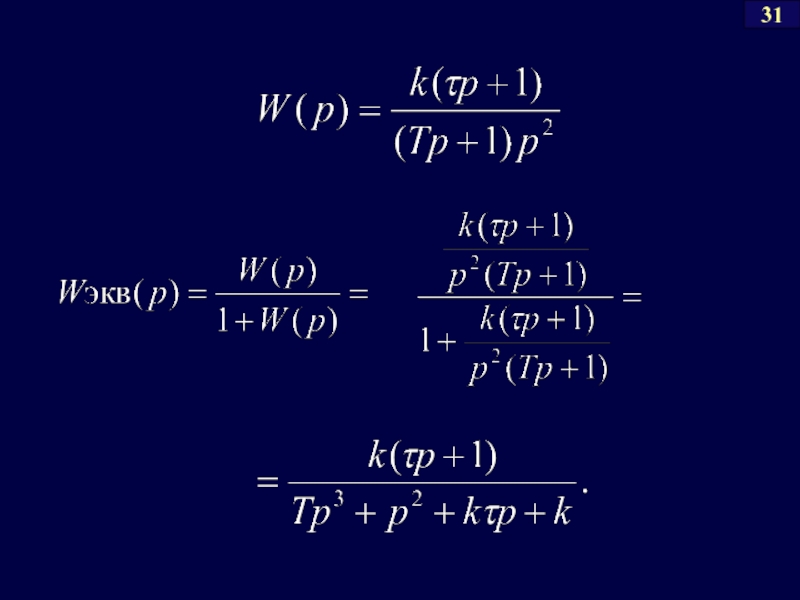- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Типовые динамические звенья систем управления презентация
Содержание
- 1. Типовые динамические звенья систем управления
- 2. П Л А Н Л
- 3. 3. ТОЖДЕСТВЕННЫЕ ПРЕОБРАЗОВАНИЯ СТРУКТУРНЫХ СХЕМ . ТИПОВЫЕ
- 4. Звеном СУ называется ее элемент, обладающий определенными
- 5. 1. КЛАССИФИКАЦИЯ ЗВЕНЬЕВ САУ Звеном
- 6. Классификация звеньев 9 - идеальное интегрирующее
- 7. 10 РЕАЛЬНЫЕ (ДИНАМИЧЕСКИЕ ) ЗВЕНЬЯ инерционное
- 8. 2. ВРЕМЕННЫЕ ХАРАКТЕРИСТИКИ ЗВЕНЬЕВ САУ 11
- 9. 12 2.1. Усилительное звено Примеры:
- 10. 13 1. Передаточная функция: 2. Операторное уравнение: 3. Дифференциальное уравнение: 2.2. ДИФФЕРЕНЦИРУЮЩЕЕ ЗВЕНО
- 11. 14 Идеальное дифференцирующее. При ступенчатом входном
- 12. Большинство объектов, которые представляют собой дифференцирующие звенья,
- 13. 16 1. Передаточная функция: 2. Операторное уравнение:
- 14. Идеальное интегрирующее Выходная величина идеального интегрирующего
- 15. Реальное интегрирующее. Примером интегрирующего звена
- 16. 19 1. Передаточная функция: 2. Операторное уравнение: 3. Дифференциальное уравнение: 2.4. АПЕРИОДИЧЕСКОЕ ЗВЕНО
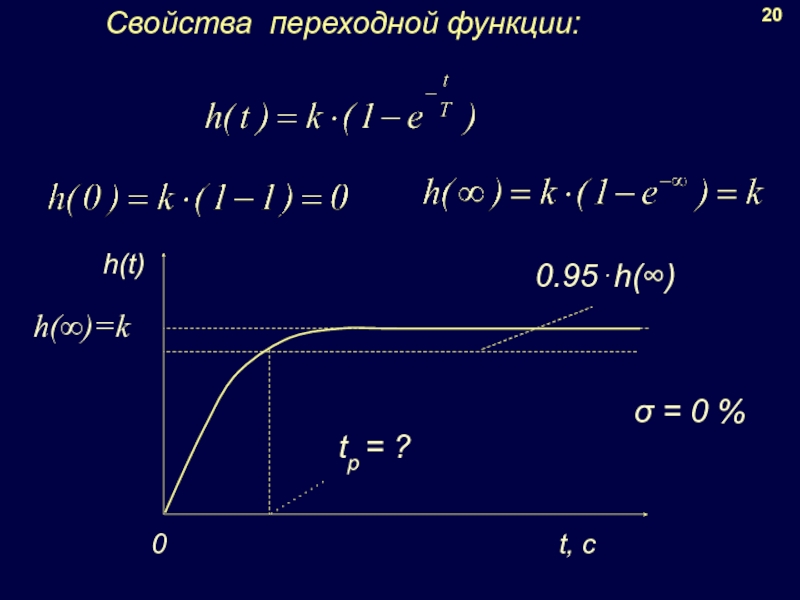
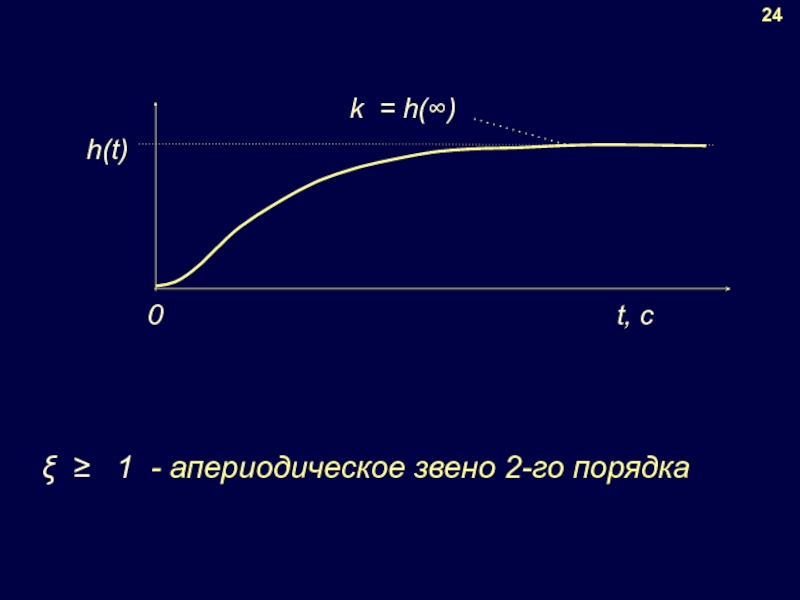
- 17. 20 Свойства переходной функции: h(∞)=k σ = 0 %
- 18. Определение времени регулирования: 21
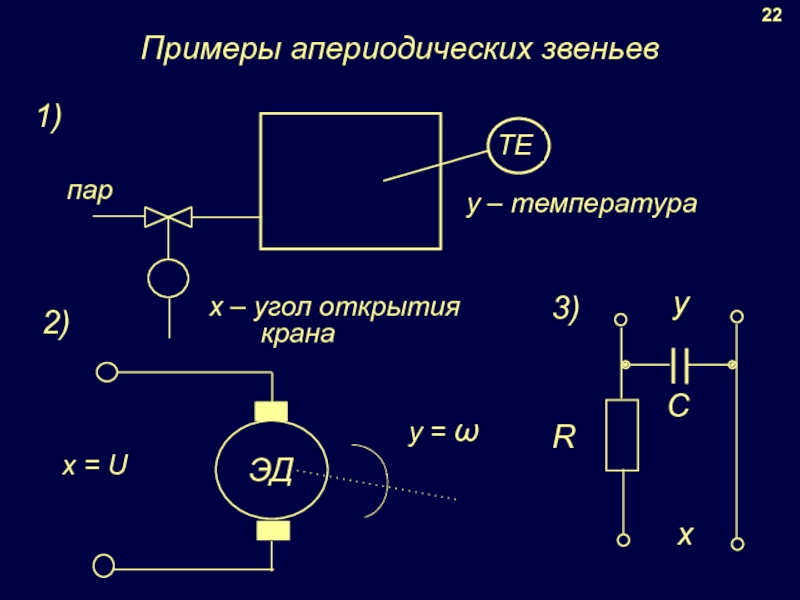
- 19. 22 Примеры апериодических звеньев x
- 20. 23 2.5. КОЛЕБАТЕЛЬНОЕ ЗВЕНО ПФ: При
- 21. 24 ξ ≥ 1 - апериодическое звено 2-го порядка
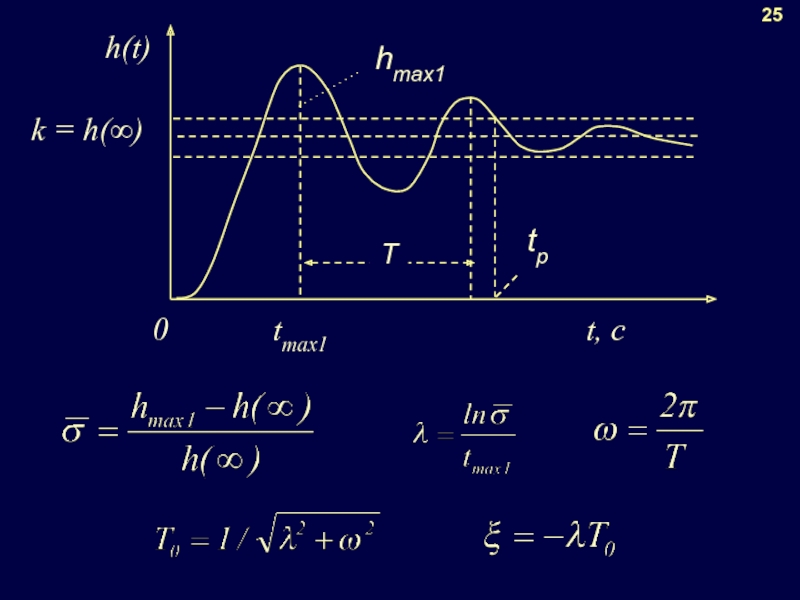
- 22. k = h(∞) hmax1 25
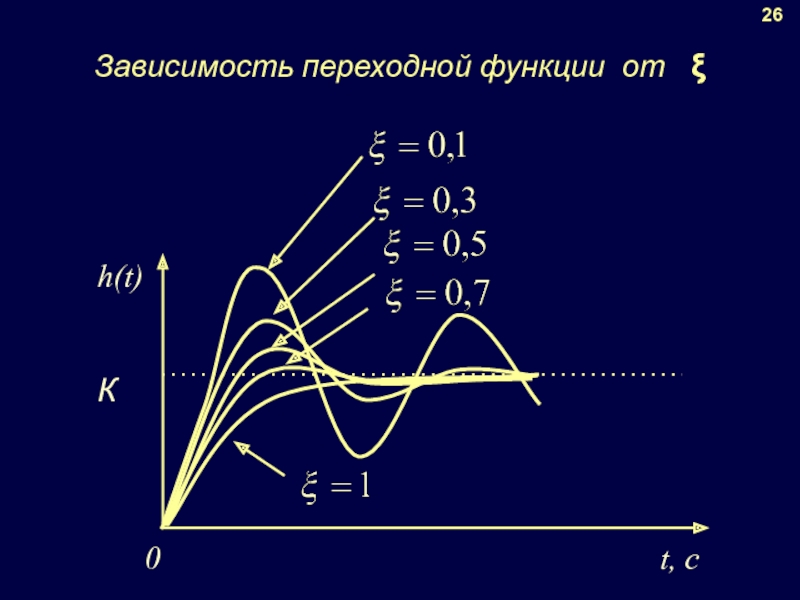
- 23. Зависимость переходной функции от ξ 26
- 24. 27 Оптимальная переходная функция ξopt = 0.707 tР ≈ 3 T σ < 5%
- 25. 28 ПРИМЕРЫ КОЛЕБАТЕЛЬНЫХ ЗВЕНЬЕВ: Колебания –
- 26. 2.6. ЗАПАЗДЫВАНИЕ В САУ 29 Звеном
- 27. Переходная функция звена с запаздыванием 30 τ
- 28. Простейшие типовые звенья: усилительное,
- 29. 1. Понятие об устойчивости САР
- 30. Выдающийся русский ученый А.М.Ляпунов основоположник
- 31. В САУ, работающей по отклонению, регулятор изменяет
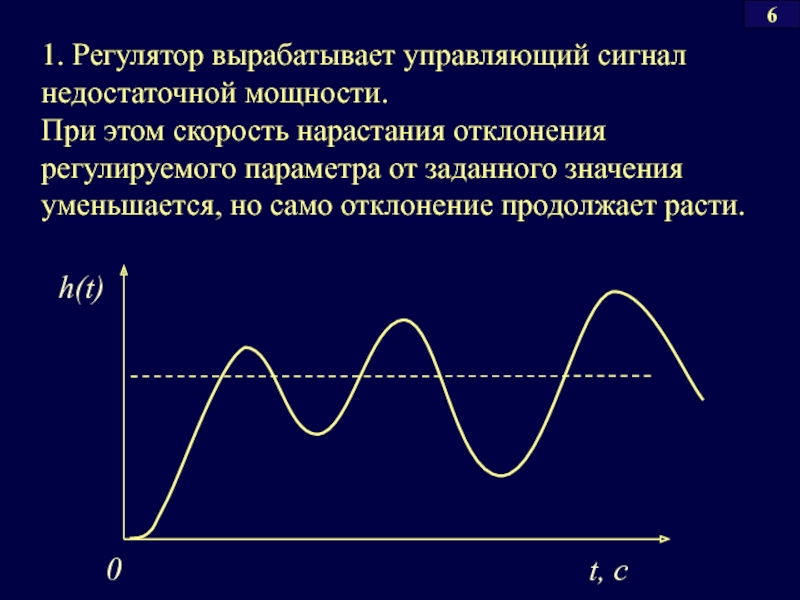
- 32. 1. Регулятор вырабатывает управляющий сигнал недостаточной мощности.
- 33. 2. Регулятор вырабатывает управляющий сигнал избыточной мощности,
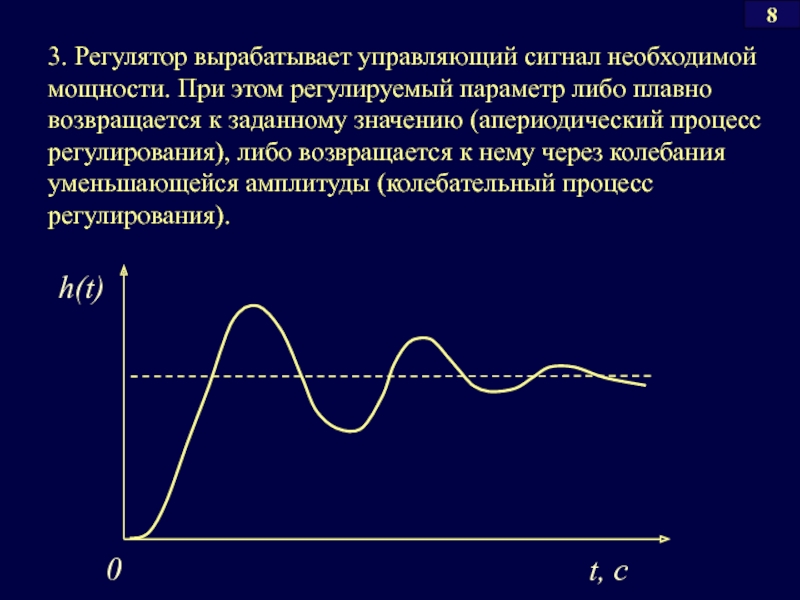
- 34. 3. Регулятор вырабатывает управляющий сигнал необходимой
- 35. 4.Понятие устойчивости. Критерии устойчивости. САР называется асимптотически
- 36. 1.2. Корневой критерий. Корневой критерий определяет устойчивость
- 37. Путем приравнивания знаменателя к нулю можно получить
- 38. ( Символом обозначены корни
- 39. (находились слева от мнимой оси на комплексной
- 40. 14 Если часть корней характеристического уравнения
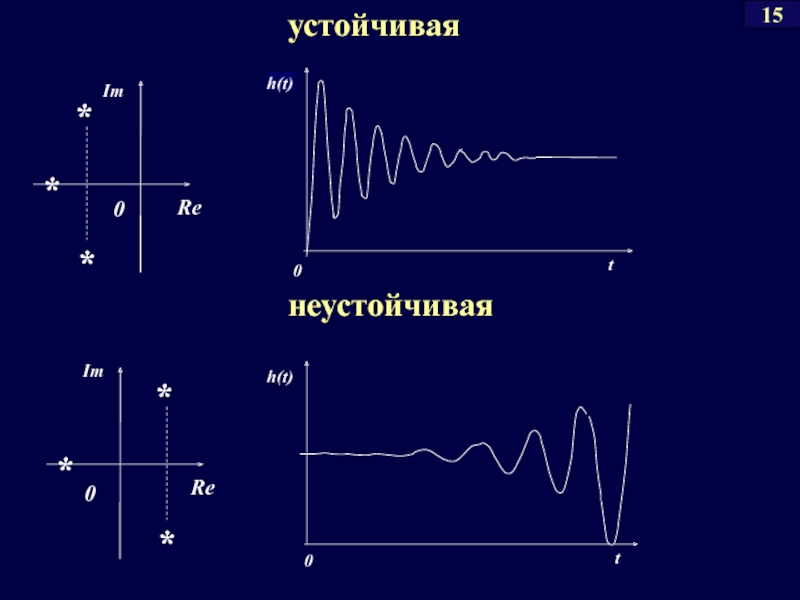
- 41. устойчивая неустойчивая 15
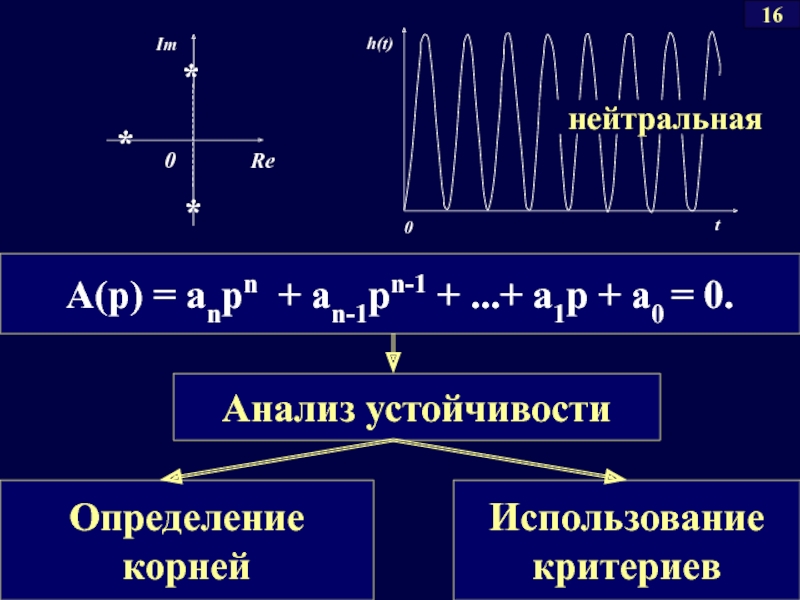
- 42. A(p) = anpn + an-1pn-1 + ...+ a1p + a0 = 0. 16
- 43. 2. Алгебраические критерии устойчивости непрерывных САР 2.1.
- 44. A(p) = an (p – p1 )(p
- 45. Необходимые условия устойчивости : Если линейная стационарная
- 46. САР неустойчива - a2 < 0.
- 47. 2.2. Критерий устойчивости Гурвица A(p)=an
- 48. an-1 a1 an a2 a3 … a2
- 49. Критерий Гурвица: Для того, чтобы корни
- 50. Критерий Гурвица САР 2-го порядка. A(p) =
- 51. Для САР 2-го порядка необходимые условия являются
- 52. Критерий Вышнеградского 26
- 53. Для того, чтобы САР 3-го порядка
- 54. 3. Области устойчивости САР Как влияют на
- 55. . Границы области устойчивости имеют штриховку, направленную
- 56. 30
- 57. 31
- 58. По критерию
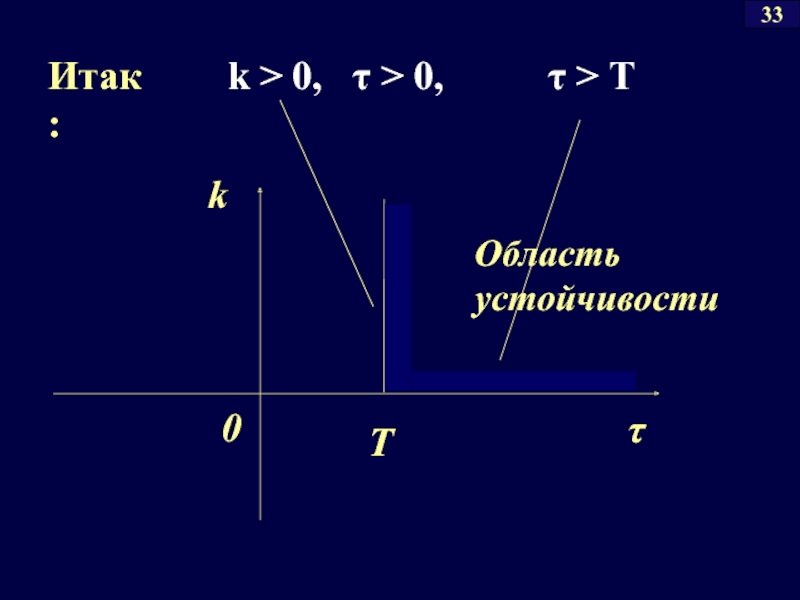
- 59. k > 0, τ > 0,
Слайд 2 П Л А Н Л Е К Ц И
2
Слайд 33. ТОЖДЕСТВЕННЫЕ ПРЕОБРАЗОВАНИЯ СТРУКТУРНЫХ СХЕМ . ТИПОВЫЕ СОЕДИНЕНИЯ (последовательное, параллельное, параллельное-встречное).
4.
Слайд 4Звеном СУ называется ее элемент, обладающий определенными свойствами в динамическом отношении.
Звенья регулирования могут иметь разную физическую основу (электрические, пневматические, механические и др. звенья), но относится к одной группе.
Соотношение входных и выходных сигналов в звеньях одной группы описываются одинаковыми передаточными функциями.
4
Слайд 51. КЛАССИФИКАЦИЯ ЗВЕНЬЕВ САУ
Звеном называется часть САУ, оператор которой
5
Применив преобразование Лапласа,
получим операторное уравнение звена:
Слайд 6Классификация звеньев
9
- идеальное интегрирующее
- усилительное звено
- идеальное дифференцирующее
ИДЕАЛЬНЫЕ ЗВЕНЬЯ
РЕАЛЬНЫЕ (ДИНАМИЧЕСКИЕ
- форсирующее 1-го порядка
форсирующее
2-го порядка
Слайд 710
РЕАЛЬНЫЕ (ДИНАМИЧЕСКИЕ ) ЗВЕНЬЯ
инерционное 1-го порядка
(апериодическое)
инерционное
2-го порядка:
колебательное
апериодическое 2-го порядка
консервативное
неустойчивое
Слайд 82. ВРЕМЕННЫЕ ХАРАКТЕРИСТИКИ ЗВЕНЬЕВ САУ
11
2.1. Усилительное звено
1. Передаточная функция:
2. Операторное уравнение:
3.
Слайд 1013
1. Передаточная функция:
2. Операторное уравнение:
3. Дифференциальное уравнение:
2.2. ДИФФЕРЕНЦИРУЮЩЕЕ ЗВЕНО
Слайд 1114
Идеальное дифференцирующее.
При ступенчатом входном сигнале выходной сигнал представляет собой импульс
Идеальные дифференцирующие звенья физически не реализуемы.
То есть, на выходе появляется единичный импульс, усиленный в k раз.
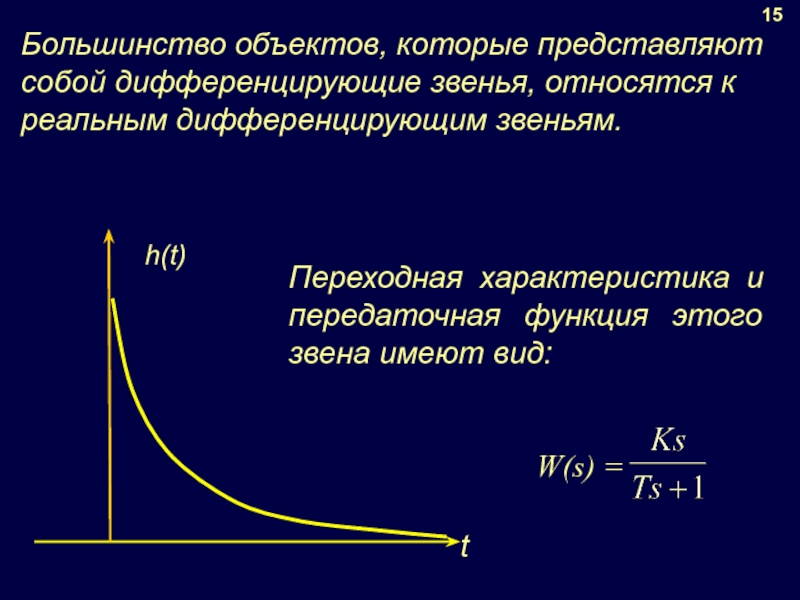
Слайд 12Большинство объектов, которые представляют собой дифференцирующие звенья, относятся к реальным дифференцирующим
15
Слайд 1316
1. Передаточная функция:
2. Операторное уравнение:
3. Дифференциальное уравнение этого звена устанавливает пропорциональность
2.3. ИНТЕГРИРУЮЩЕЕ ЗВЕНО
или
Слайд 14Идеальное интегрирующее
Выходная величина идеального интегрирующего звена пропорциональна интегралу входной величины.
При подаче на вход звена воздействия выходной сигнал постоянно возрастает.
Это звено астатическое, т.е. не имеет установившегося режима.
у
t
17
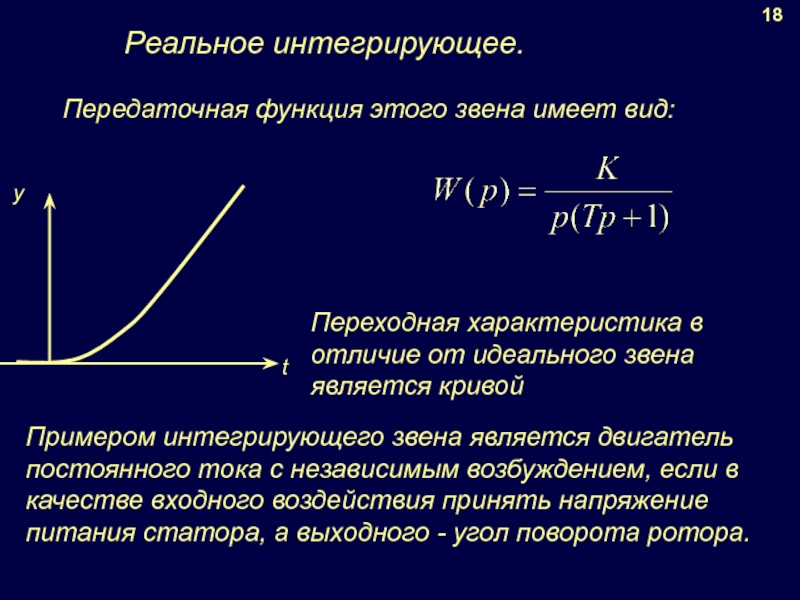
Слайд 15Реальное интегрирующее.
Примером интегрирующего звена является двигатель постоянного тока с независимым
18
Слайд 1619
1. Передаточная функция:
2. Операторное уравнение:
3. Дифференциальное уравнение:
2.4. АПЕРИОДИЧЕСКОЕ ЗВЕНО
Слайд 2023
2.5. КОЛЕБАТЕЛЬНОЕ ЗВЕНО
ПФ:
При подаче на вход ступенчатого воздействия амплитудой х0
колебательный (при ).
Слайд 2528
ПРИМЕРЫ КОЛЕБАТЕЛЬНЫХ ЗВЕНЬЕВ:
Колебания –
результат
взаимодействия сил
- электрические цепи,
включающие активное сопротивление, емкость
- автомобиль на пружинном подвесе
с амортизаторами,
- механические весы,
Слайд 262.6. ЗАПАЗДЫВАНИЕ В САУ
29
Звеном с запаздыванием называется
элемент САУ, оператор
Слайд 28Простейшие типовые звенья:
усилительное,
интегрирующее,
дифференцирующее,
апериодическое,
колебательное,
запаздывающее
Слайд 29
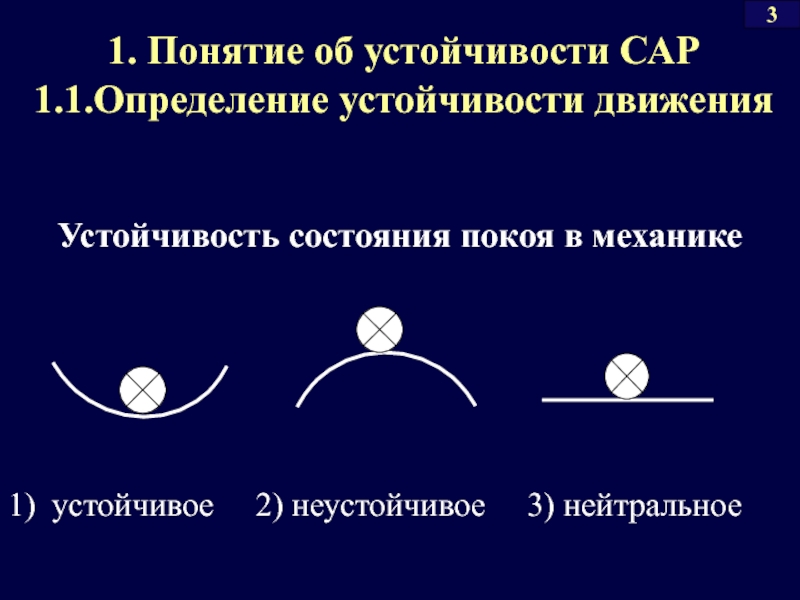
1. Понятие об устойчивости САР
1.1.Определение устойчивости движения
1) устойчивое 2)
Устойчивость состояния покоя в механике
3
Слайд 30Выдающийся русский ученый А.М.Ляпунов
основоположник учения об устойчивости
движения, в
покоя выбрал невозмущенное движение
Невозмущенным называется движение
САР при отсутствии возмущений.
САР называется устойчивой, если она, будучи выведенной из состояния невозмущенного движения некоторым возмущением, приходит вновь в это состояние или близкое к нему после прекращения действия этого возмущения.
4
Слайд 31В САУ, работающей по отклонению, регулятор изменяет управляющий сигнал после того,
5
Слайд 321. Регулятор вырабатывает управляющий сигнал недостаточной мощности.
При этом скорость нарастания
6
Слайд 332. Регулятор вырабатывает управляющий сигнал избыточной мощности, который не только компенсирует
7
Слайд 34
3. Регулятор вырабатывает управляющий сигнал необходимой мощности. При этом регулируемый параметр
8
Слайд 354.Понятие устойчивости. Критерии устойчивости.
САР называется асимптотически
устойчивой, если при указанных выше
Причина движения САР после
прекращения действия возмущения
– ненулевые начальные условия
Далее устойчивая САР –
это асимптотически устойчивая САР
9
Слайд 361.2. Корневой критерий.
Корневой критерий определяет устойчивость системы по виду передаточной функции.
Динамической характеристикой системы, описывающей основные поведенческие свойства, является характеристический полином, находящийся в знаменателе передаточной функции.
10
Слайд 37Путем приравнивания знаменателя к нулю можно получить характеристическое уравнение, по корням
Корни характеристического уравнения могут быть как действительные, так и комплексные и для определения устойчивости откладываются на комплексной плоскости
11
Слайд 38( Символом обозначены корни уравнения).
Виды корней характеристического уравнения:
-
положительные (корень 1);
отрицательные (2);
нулевые (3);
- Комплексные
комплексные сопряженные (4);
чисто мнимые (5);
*
12
Слайд 39(находились слева от мнимой оси на комплексной плоскости ).
1.3. Необходимые
13
Для того, чтобы линейная стационарная
САР была асимптотически устойчивой по
Ляпунову необходимо и достаточно,
чтобы корни ее характеристического
уравнения имели отрицательные
действительные части
Слайд 4014
Если часть корней характеристического
уравнения САР находятся на мнимой оси,
1.3. Необходимые и достаточные условия устойчивости САР
Слайд 432. Алгебраические критерии устойчивости непрерывных САР
2.1. Необходимые условия устойчивости
Пусть A(p)
A(p) = an (p – p1 )(p – p2 )...(p – pn ),
где рi корни уравнения A(p) = 0.
17
Слайд 44A(p) = an (p – p1 )(p – p2 )...(p –
Если p1 = - α < 0 устойчивый корень,
(p – p1) = (p + α) - двучлен
с положительными коэффициентами,
Если p1 = - α + j β; p2 = - α - j β;
α > 0; β > 0 - устойчивые корни,
(р – р1 )(р – р2 ) = (p + α - j β)(p + α + j β) =
= p2 + 2α p + α2+β2, 2 α > 0, α2 + β2 >0
18
Слайд 45Необходимые условия устойчивости : Если линейная стационарная
САР устойчива, то все
её характеристического полинома
больше нуля.
Это значит, что если
19
Слайд 46САР неустойчива - a2 < 0.
A(p) = p3
3) A(p) = p3 + p2 + 4 p + 20; все ai > 0 -
A(p) = p3- 3 p2+ 2p+1 -
САР неустойчива - a2 = 0.
САР необходимо доп. исследовать
Примеры:
20
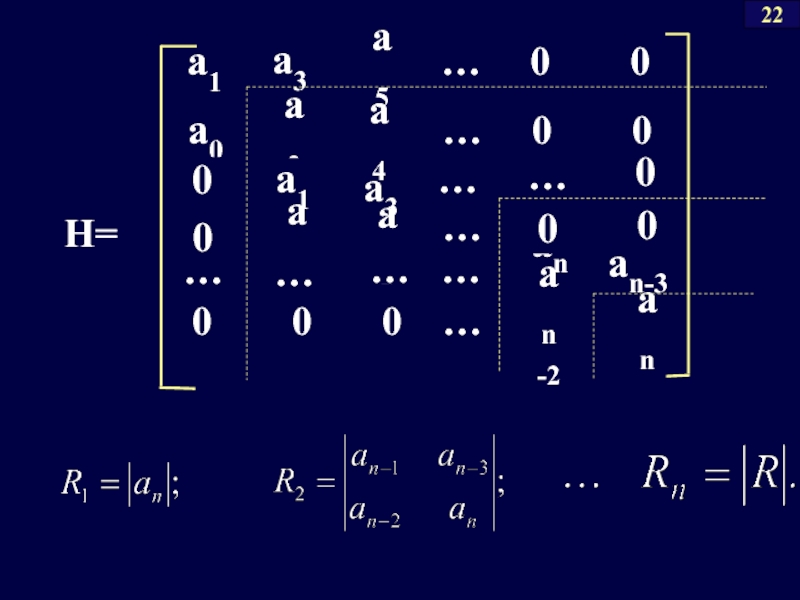
Слайд 472.2. Критерий устойчивости Гурвица
A(p)=an pn+ ... + a1p +
Правила написания матрицы Гурвица:
на главной диагонали - a0 , a1, ..., an-1
в порядке увеличения индексов
сверху вниз;
2) строки - в порядке увеличения
индексов слева направо, при этом
ai = 0, при i < 0 и i > n.
21
Слайд 49Критерий Гурвица:
Для того, чтобы корни
характеристического уравнения
САР при аn
23
Слайд 51Для САР 2-го порядка необходимые
условия являются и достаточными
Критерий Гурвица САР 3-го
Критерий Вышнеградского
A(p) = a3p3 + a2p2 + a1p + a0= 0; a3 > 0;
25
Слайд 53Для того, чтобы САР 3-го порядка была устойчивой, необходимо и
Критерий Вышнеградского
27
Слайд 543. Области устойчивости САР
Как влияют на устойчивость САР
ее параметры?
Пространство параметров,
Области устойчивости очерчиваются линиями (границами), которые опре-деляются по критериям устойчивости.
28
Слайд 55. Границы области устойчивости имеют штриховку, направленную в сторону области устойчивости.
Пример.
Дано:
область
Требуется определить:
структурная схема САР
29