- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Тепломассообмен. Задачи. Теплопроводность презентация
Содержание
- 1. Тепломассообмен. Задачи. Теплопроводность
- 2. План 1. Теплопроводность через однослойную и многослойную плоские стенки. 2. Теплопроводность через цилиндрическую стенку.
- 3. 1. Теплопроводность через однослойную и многослойную плоские стенки
- 4. При стационарном тепловом режиме температурное поле внутри
- 5. Для многослойной плоской стенки (3)
- 6. При расчете тепловых потерь через стенки печи
- 7. Коэффициент теплоотдачи конвекцией αо может быть
- 8. Пример № 1. Определить тепловой поток
- 9. Пример № 1. Решение. 1. По
- 10. Пример № 2. Определить коэффициент теплопроводности материала
- 11. Пример № 3. Определить потерю тепла через
- 12. Решение. 1. Находим коэффициенты теплопроводности шамотного и
- 13. Обозначим температуру на границе раздела слоев t'
- 14. Принимаем температуру наружной поверхности стенки tн =
- 15. или с учетом зависимости коэффициентов теплопроводности от
- 16. Решим это уравнение относительно t′, ° С,
- 17. Определим средние температуры по толщине слоев материалов,
- 18. для диатомитового кирпича λд = 0,145 + 0,0003·345=0,2485 Вт/(м·К).
- 19. 2. Найдем коэффициент теплоотдачи конвекцией от наружной
- 20. 3. Определим удельный тепловой поток, q, Вт/м2,
- 21. 4. Проверим принятое ранее значение температуры наружной
- 22. Пример № 4. Вычислить плотность теплового потока,
- 23. Решение. Плотность теплового потока для многослойной стенки определяем по уравнению (3),
- 24. При замене изоляционной прослойки красным кирпичом
- 25. Экономия от применения изоляционной прослойки,
- 26. Температуру между изоляционной прослойкой и красным кирпичом определяем по формуле:
- 27. Температуру между шамотным и красным кирпичом:
- 28. Пример № 5. Плоская стальная стена с
- 29. Решение. Эквивалентная теплопроводность для трехслойной стенки определяется из уравнения:
- 30. Для новой изоляции при одинаковых потерях эквивалентная
- 31. 2. Теплопроводность через цилиндрическую стенку
- 32. Для расчета теплопроводности через однослойную цилиндрическую стенку
- 33. Закон Фурье для теплового потока, проходящего через
- 34. Для многослойной цилиндрической поверхности тепловой поток определяется из выражения: (7)
- 35. Если dнар/dвн < 2, то с достаточной
- 36. Пример № 1. Стальная труба, отношение диаметров
- 37. Решение. Из условия задачи следует, что d1=0,2
- 38. Температуру между слоями найдем по уравнениям:
- 39. Температуру между слоями найдем по уравнениям:
План 1. Теплопроводность через однослойную и многослойную плоские стенки. 2. Теплопроводность через цилиндрическую стенку.
Слайд 2План
1. Теплопроводность через однослойную и многослойную плоские стенки.
2. Теплопроводность через цилиндрическую
стенку.
Слайд 4При стационарном тепловом режиме температурное поле внутри нагреваемого тела не меняется
во времени, т.е. dt/dτ = 0.
Плотность теплового потока для плоской стенки можно определить по формуле Фурье:
или
где q = const – тепловой поток, Вт/м2; t1, t2 – температуры на поверхностях стенки, °C; δ – толщина стенки, м; λ – коэффициент теплопроводности, Вт/(м∙К); R – тепловое сопротивление, (м2∙К)/Вт.
Плотность теплового потока для плоской стенки можно определить по формуле Фурье:
или
где q = const – тепловой поток, Вт/м2; t1, t2 – температуры на поверхностях стенки, °C; δ – толщина стенки, м; λ – коэффициент теплопроводности, Вт/(м∙К); R – тепловое сопротивление, (м2∙К)/Вт.
(1)
(2)
Слайд 6При расчете тепловых потерь через стенки печи в окружающую среду следует
пользоваться формулой
где Rп – тепловое сопротивление при переходе от источника тепла к внутренней поверхности стены, (м2∙К)/Вт;
практически можно принять Rп = 0 и считать, что температура источника тепла (газа) равна температуре внутренней поверхности кладки, 1/αп;
Rст – тепловое сопротивление многослойной (однослойной) стенки печи, ∑δ/λ;
Ro – тепловое сопротивление при переходе от наружной поверхности стены в окружающую среду 1/αо.
где Rп – тепловое сопротивление при переходе от источника тепла к внутренней поверхности стены, (м2∙К)/Вт;
практически можно принять Rп = 0 и считать, что температура источника тепла (газа) равна температуре внутренней поверхности кладки, 1/αп;
Rст – тепловое сопротивление многослойной (однослойной) стенки печи, ∑δ/λ;
Ro – тепловое сопротивление при переходе от наружной поверхности стены в окружающую среду 1/αо.
(4)
Слайд 7Коэффициент теплоотдачи конвекцией αо может быть рассчитан по формуле
или для
приближенных расчетов принят равным αо=11,63 Вт/(м2∙К).
αо = 1,163∙(8 + 0,05∙tнар),
(5)
Слайд 8Пример № 1.
Определить тепловой поток через бетонную стену здания толщиной δ
= 200 мм, высотой Н = 2,5 м и длиной l = 2 м. если температуры на ее поверхностях tc1 = 20ºC, tc2 = – 10ºC, а коэффициент теплопроводности λ = 1 Вт/(м·К).
Слайд 9Пример № 1.
Решение.
1. По формуле (1) определим удельный тепловой поток
2.
Определим тепловой поток через стену, умножив удельный тепловой поток на площадь стены
Слайд 10Пример № 2.
Определить коэффициент теплопроводности материала стены толщиной 50 мм, если
плотность теплового потока через нее q = 100 Вт/м2, а разность температур Δt = 20 °C.
Решение.
1. Определим коэффициент теплопроводности материала стены из формулы (1)
Решение.
1. Определим коэффициент теплопроводности материала стены из формулы (1)
Слайд 11Пример № 3.
Определить потерю тепла через стенку методической печи при стационарном
режиме, если температура внутренней поверхности кладки tк = tп = 1300°C, температура окружающей среды tо = 0°C. Толщина шамотной кладки стенки δш = 0,46 м; толщина изоляционной кладки из диатомитового кирпича δд = 0,115 м.
Слайд 12Решение.
1. Находим коэффициенты теплопроводности шамотного и диатомитового кирпича [1], Вт/(м·К),
для шамотного
кирпича λш = 0,7 + 0,00064 tср.ш;
для диатомитового кирпича λд = 0,145 + 0,0003 tср.д.
для диатомитового кирпича λд = 0,145 + 0,0003 tср.д.
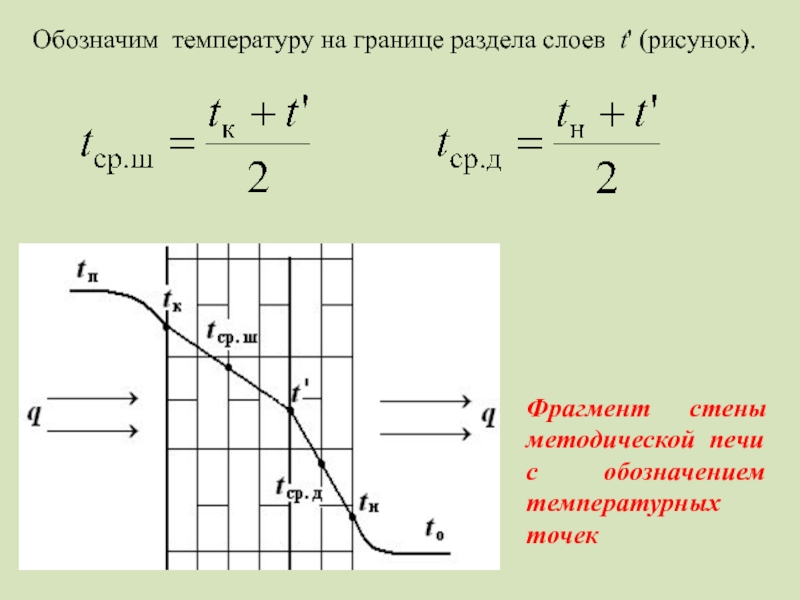
Слайд 13Обозначим температуру на границе раздела слоев t' (рисунок).
Фрагмент стены методической печи
с обозначением температурных точек
Слайд 14Принимаем температуру наружной поверхности стенки tн = 100 °C.
Передача тепла
происходит при стационарном режиме, т. е. при q= const, тогда можно записать равенство удельных тепловых потоков слева и справа:
или с учетом зависимости коэффициентов теплопроводности от температуры:
или с учетом зависимости коэффициентов теплопроводности от температуры:
Слайд 15или с учетом зависимости коэффициентов теплопроводности от температуры:
получим квадратное уравнение:
0,00000132(t')2 +
0,000925t' – 1,0 = 0
Слайд 17Определим средние температуры по толщине слоев материалов,
для шамотного кирпича:
λш = 0,7
+ 0,00064·945=1,31 Вт/(м·К).
Слайд 192. Найдем коэффициент теплоотдачи конвекцией от наружной поверхности стенки к окружающей
среде по формуле (5)
αо = 1,163∙(8 + 0,05∙tнар),
αо = 1,163∙(8 + 0,05∙100)=15,15 Вт/(м2·К).
Слайд 214. Проверим принятое ранее значение температуры наружной поверхности стенки:
откуда
так как
принятая ранее температура наружной поверхности tн = 100 °C, а полученная расчетом tн = 95,5 °C и погрешность которой составляет Δ = 4,5 %. Это допустимо. Расчет считаем законченным.
Слайд 22Пример № 4.
Вычислить плотность теплового потока, проходящего через стенку неэкранированной топочной
камеры парового котла толщиной 625 мм. Стенка состоит из трех слоев: одного шамотного кирпича толщиной 250 мм, изоляционной прослойки из мелкого шлака толщиной 125 мм и одного красного кирпича толщиной 250 мм. Температура на внутренней поверхности топочной камеры tк = tп = 1527°C, а наружной tн = 47°C.
Теплопроводности: шамотного кирпича λ1=1,28 Вт/(м·К), изоляционной прослойки λ2=0,15 Вт/(м·К) и красного кирпича λ3=0,8 Вт/(м·К).
Как изменится тепловой поток в стенке, если изоляционную прослойку заменить красным кирпичом? Определить экономию в процентах от применения изоляционной прослойки. Кроме того, определить температуру между слоями.
Теплопроводности: шамотного кирпича λ1=1,28 Вт/(м·К), изоляционной прослойки λ2=0,15 Вт/(м·К) и красного кирпича λ3=0,8 Вт/(м·К).
Как изменится тепловой поток в стенке, если изоляционную прослойку заменить красным кирпичом? Определить экономию в процентах от применения изоляционной прослойки. Кроме того, определить температуру между слоями.
Слайд 25Экономия от применения изоляционной прослойки,
Температуру между шамотным кирпичом и изоляционной прослойкой
определяем по формуле:
Слайд 27Температуру между шамотным и красным кирпичом:
Из расчета видно, изоляционная прослойка не
только уменьшает тепловые потери, но и сохраняет кладку из красного кирпича.
При температурах выше 900 °С красный кирпич быстро разрушается.
При температурах выше 900 °С красный кирпич быстро разрушается.
Слайд 28Пример № 5.
Плоская стальная стена с λ1=50 Вт/(м·К) и толщиной δ1=0,02
м изолирована от тепловых потерь слоем асбестового картона с λ2=0,15 Вт/(м·К) толщиной δ2=0,2 м и слоем пробки λ3=0,045 Вт/(м·К) толщиной δ3=0,1 м. Определить, какой толщины необходимо взять слой пенобетона с λ=0,08 Вт/(м·К) вместо асбеста и пробки, чтобы теплоизоляционные свойства стенки остались без изменения.
Слайд 30Для новой изоляции при одинаковых потерях эквивалентная теплопроводность остается такой же,
как и у трехслойной стенки, поэтому
откуда
Слайд 32Для расчета теплопроводности через однослойную цилиндрическую стенку необходимо учитывать условие, что
удельный тепловой поток q = Q∕F ≠ const, поскольку площадь F = 2πr·l, через которую проходит тепловой поток, зависит от радиуса, переменной величины.
Слайд 33Закон Фурье для теплового потока, проходящего через однослойную цилиндрическую стенку, будет
иметь вид:
для цилиндрической поверхности плотность теплового потока относят на 1 м ее длины.
для цилиндрической поверхности плотность теплового потока относят на 1 м ее длины.
(6)
Слайд 35Если dнар/dвн < 2, то с достаточной точностью, в практических расчетах,
можно определить тепловой поток по формулам для плоской стенки (2) и (3).
В этом случае в качестве диаметра трубы следует принимать средний диаметр
В этом случае в качестве диаметра трубы следует принимать средний диаметр
Слайд 36Пример № 1.
Стальная труба, отношение диаметров которой d1/d2=200/220 мм и теплопроводность
λ1 = 50 Вт/(м·К), покрыта двухслойной изоляцией. Толщина первого слоя δ2 = 50 мм с теплопроводностью λ2 = 0,2 Вт/(м·К) и второго δ3 = 80 мм с λ3=0,1 Вт/(м·К). Температура внутренней поверхности трубы tcт1 = 327 ºC и наружной поверхности изоляции tcт2 =47 ºC. Определить тепловые потери теплоты через изоляцию с 1 м длины трубопровода и температуры на границе соприкосновения отдельных слоев.
Слайд 37Решение.
Из условия задачи следует, что d1=0,2 м, d2=0,22 м, d3=0,32 м,
и d4=0,48 м.
Согласно уравнению (7) получаем
Согласно уравнению (7) получаем
