- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Тепломассообмен. Теплопроводность при стационарном тепловом режиме (часть 1) презентация
Содержание
- 1. Тепломассообмен. Теплопроводность при стационарном тепловом режиме (часть 1)
- 2. План 1. Передача теплоты через однослойную плоскую
- 3. 1. Передача теплоты через однослойную плоскую стенку
- 4. Теплопроводность через однослойную плоскую стенку (самый распространенный
- 5. При этих условиях температурное поле в стенке
- 6. Из этого уравнения следует, что температура изменяется
- 7. Константа интегрирования С определяется из условий на
- 8. Общее количество теплоты QT, которое передается через
- 9. Тепловой поток Q зависит не от абсолютного
- 10. Распределение температур при постоянном и переменном коэффициентах
- 11. В уравнение Введем поправки на
- 12. При граничных значениях переменных имеем: при
- 13. Множитель
- 14. Уравнение температурной кривой в стенке получается путем
- 15. 2. Передача теплоты через многослойную плоскую стенку
- 16. Выведем расчетную формулу теплопроводности сложной стенки при
- 17. Рассмотрим трехслойную стенку, в которой толщина отдельных
- 18. Тепловой поток для каждого слоя:
- 19. Складывая их, получаем:
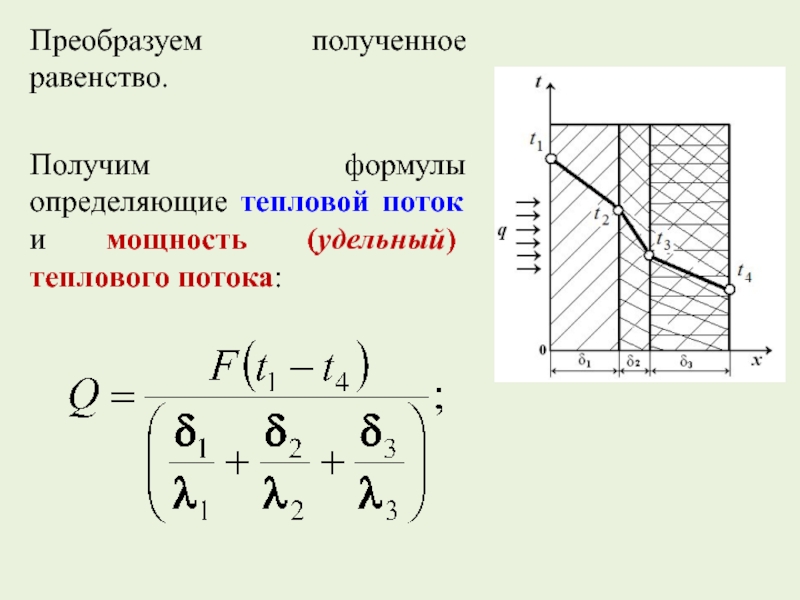
- 20. Преобразуем полученное равенство. Получим формулы определяющие тепловой поток и мощность (удельный) теплового потока:
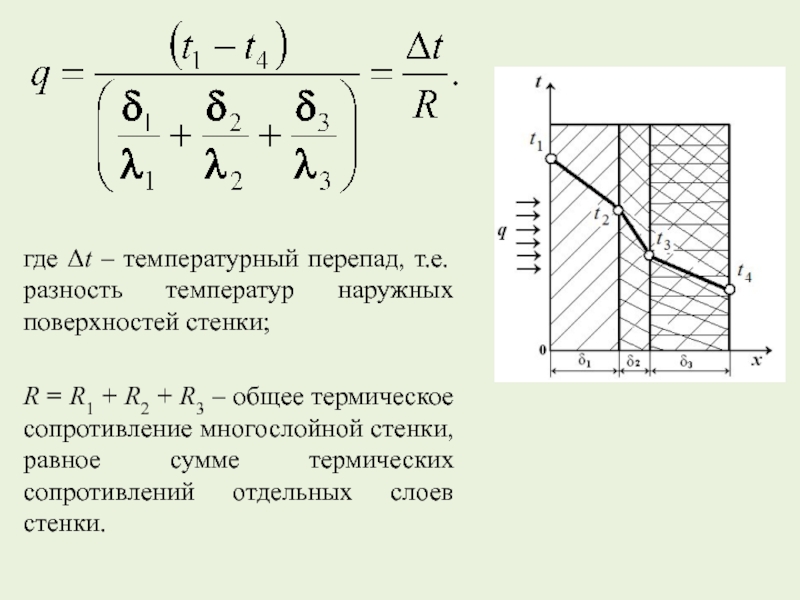
- 21. где Δt – температурный перепад, т.е. разность
- 23. Температуры (°С) между отдельными слоями сложной стенки
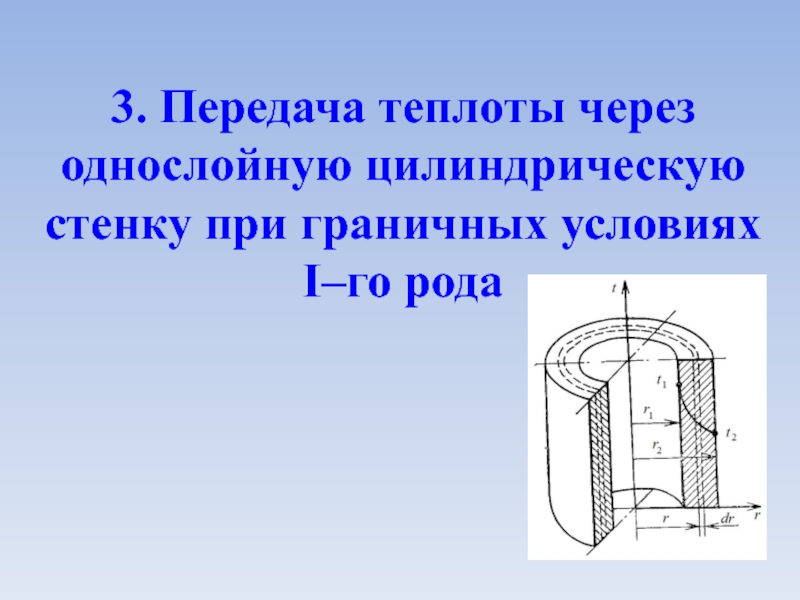
- 24. 3. Передача теплоты через однослойную цилиндрическую стенку при граничных условиях I–го рода
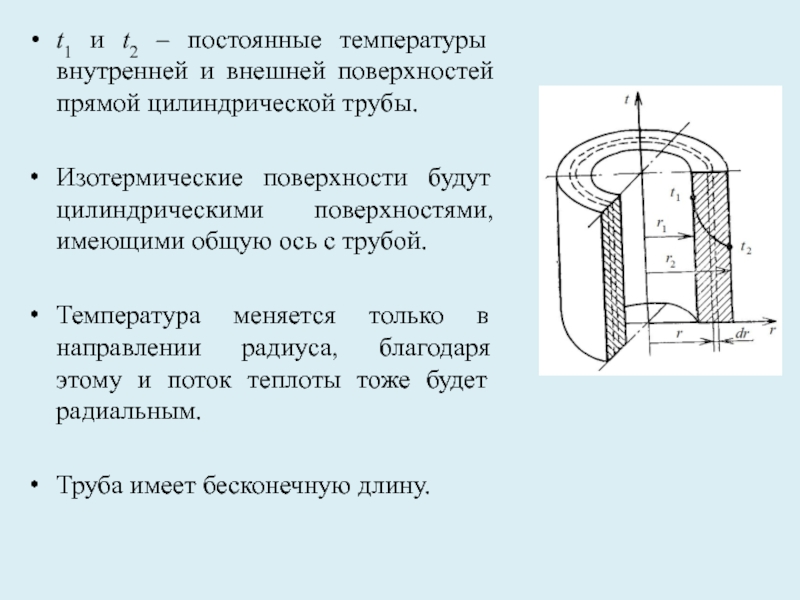
- 25. t1 и t2 – постоянные температуры внутренней
- 26. Температурное поле одномерное t=f(r), где r текущая
- 27. Рассмотрим участок трубы длинной l, в которой
- 28. Через внутреннюю и внешнюю поверхности проходит один
- 29. Разность температур между поверхностями элементарного слоя будет
- 30. Разделяя переменные, получаем
- 31. Выразим тепловой поток
- 32. Тепловой поток может быть отнесен к единице
- 33. 4. Передача теплоты через многослойную цилиндрическую стенку при граничных условиях I–го рода
- 34. Цилиндрическая стенка состоит из трех плотно прилегающих
- 35. Теплопроводность слоев равны λ1, λ2, λ3.
- 36. При стационарном режиме через все слои проходит
- 37. Решая полученные уравнения относительно разности температур и почленно складывая, получаем откуда
- 38. Температуры (°С) между слоями находим из следующих уравнений:
- 39. 5. Передача теплоты через шаровую стенку при граничных условиях I–го рода
- 40. Постоянный тепловой поток направлен через шаровую стенку.
- 41. Тепловой поток, проходящий через шаровой слой радиусом
- 42. Интегрируя данное уравнение
План 1. Передача теплоты через однослойную плоскую стенку при граничных условиях I–го рода. 2. Передача теплоты через многослойную плоскую стенку при граничных условиях I–го рода. 3. Передача теплоты через однослойную цилиндрическую
Слайд 2План
1. Передача теплоты через однослойную плоскую стенку при граничных условиях I–го
рода.
2. Передача теплоты через многослойную плоскую стенку при граничных условиях I–го рода.
3. Передача теплоты через однослойную цилиндрическую стенку при граничных условиях I–го рода.
4. Передача теплоты через многослойную цилиндрическую стенку при граничных условиях I–го рода.
5. Передача теплоты через шаровую стенку при граничных условиях I–го рода.
6. Теплопроводность тел с внутренними источниками теплоты.
2. Передача теплоты через многослойную плоскую стенку при граничных условиях I–го рода.
3. Передача теплоты через однослойную цилиндрическую стенку при граничных условиях I–го рода.
4. Передача теплоты через многослойную цилиндрическую стенку при граничных условиях I–го рода.
5. Передача теплоты через шаровую стенку при граничных условиях I–го рода.
6. Теплопроводность тел с внутренними источниками теплоты.
Слайд 31. Передача теплоты через однослойную плоскую стенку при граничных условиях I–го
рода
Дифференциальное уравнение теплопроводности позволяет определить температуру в зависимости от времени и координат в любой точке поля.
Для любого случая к нему надо присоединить необходимые краевые условия.
Слайд 4Теплопроводность через однослойную плоскую стенку (самый распространенный случай)
Длина и ширина плоской
стенки бесконечно велики по сравнению с ее толщиной δ.
Стенка имеет постоянную толщину δ.
Температуры поверхностей стенки t1 и t2 поддерживаются постоянными, т.е. они являются изотермическими поверхностями.
Температура меняется только направлении перпендикулярном плоскости стенки, которое принимаем за ось x.
Теплопроводность λ постоянна для всей стенки.
Стенка имеет постоянную толщину δ.
Температуры поверхностей стенки t1 и t2 поддерживаются постоянными, т.е. они являются изотермическими поверхностями.
Температура меняется только направлении перпендикулярном плоскости стенки, которое принимаем за ось x.
Теплопроводность λ постоянна для всей стенки.
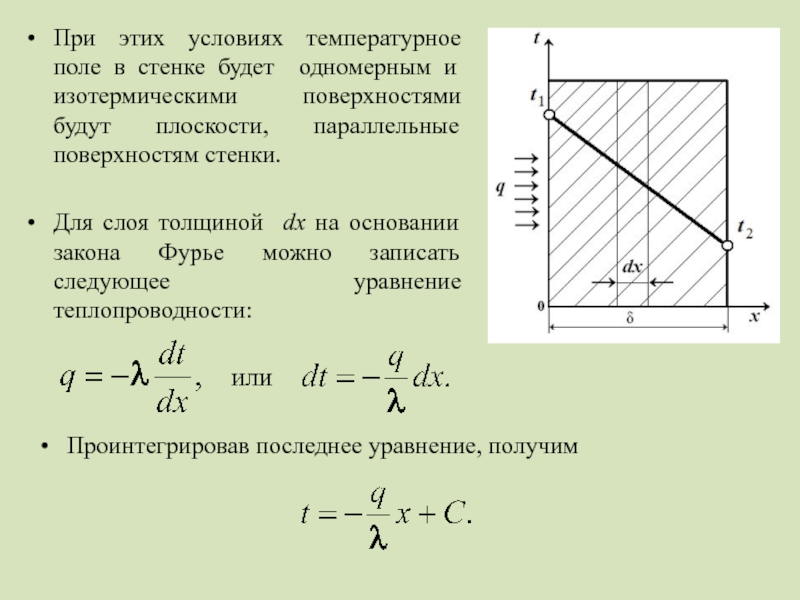
Слайд 5При этих условиях температурное поле в стенке будет одномерным и изотермическими
поверхностями будут плоскости, параллельные поверхностям стенки.
Для слоя толщиной dх на основании закона Фурье можно записать следующее уравнение теплопроводности:
Для слоя толщиной dх на основании закона Фурье можно записать следующее уравнение теплопроводности:
или
Проинтегрировав последнее уравнение, получим
Слайд 6Из этого уравнения следует, что температура изменяется по толщине стенки по
линейному закону.
Константа интегрирования С определяется из условий на границах стенки:
если х = 0, то t = t1, откуда С = t1.
Если х = δ, то t = t2 и данное уравнение принимает вид
Константа интегрирования С определяется из условий на границах стенки:
если х = 0, то t = t1, откуда С = t1.
Если х = δ, то t = t2 и данное уравнение принимает вид
Из этого уравнения определяем значение мощности теплового потока q:
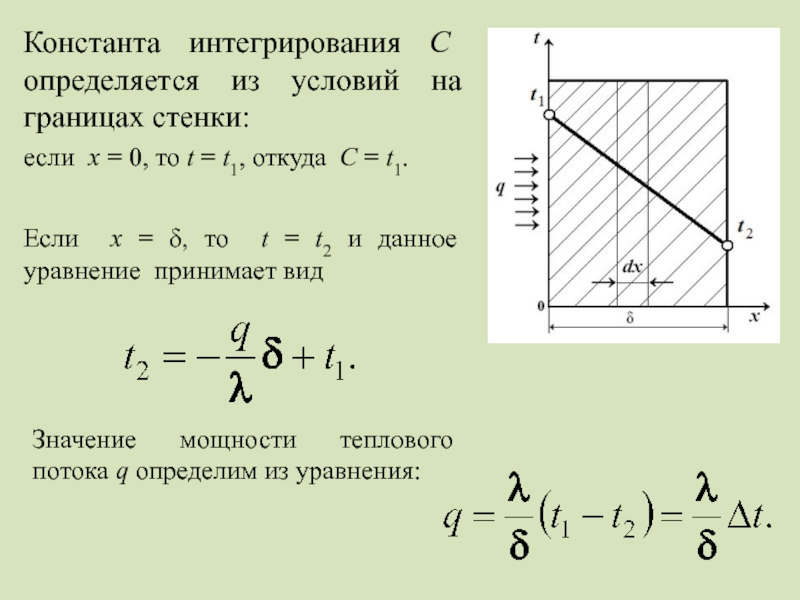
Слайд 7Константа интегрирования С определяется из условий на границах стенки:
если х =
0, то t = t1, откуда С = t1.
Если х = δ, то t = t2 и данное уравнение принимает вид
Если х = δ, то t = t2 и данное уравнение принимает вид
Значение мощности теплового потока q определим из уравнения:
Слайд 8Общее количество теплоты QT, которое передается через поверхность стенки F за
время τ:
где – тепловая проводимость стенки.
где – тепловая проводимость стенки.
Слайд 9Тепловой поток Q зависит не от абсолютного значения температур, от разности
температур на наружных поверхностях стенки:
где называется температурным напором.
где называется температурным напором.
Слайд 10Распределение температур при постоянном и переменном коэффициентах теплопроводности
Уравнение
справедливо для случая, когда
теплопроводность является постоянной величиной.
Теплопроводность реальных тел зависит от температуры и закон изменения температур выражается кривой линией.
Если теплопроводность зависит от температуры в незначительной степени, то на практике закон изменения температур считают линейным.
Теплопроводность реальных тел зависит от температуры и закон изменения температур выражается кривой линией.
Если теплопроводность зависит от температуры в незначительной степени, то на практике закон изменения температур считают линейным.
Слайд 11
В уравнение
Введем поправки на зависимость λ от t, считая эту зависимость
линейной:
Подставим эту зависимость в уравнение Фурье, получаем
Разделив переменные и интегрируя, получаем
Подставим эту зависимость в уравнение Фурье, получаем
Разделив переменные и интегрируя, получаем
Слайд 12При граничных значениях переменных имеем:
при x=0, t=t1 и
при x=δ, t=t2 и
Вычитая
из второго равенства первое, находим
Полученное уравнение позволяет определить поверхностную плотность теплового потока при переменной теплопроводности.
Полученное уравнение позволяет определить поверхностную плотность теплового потока при переменной теплопроводности.
Слайд 13Множитель
является среднеинтегральным значением теплопроводности.
В уравнении
теплопроводность λ была принята постоянной и равной среднеинтегральному значению теплопроводности λср.
Плотность (мощность) теплового потока можем определить по формуле
В уравнении
теплопроводность λ была принята постоянной и равной среднеинтегральному значению теплопроводности λср.
Плотность (мощность) теплового потока можем определить по формуле
Слайд 14Уравнение температурной кривой в стенке получается путем решения квадратного уравнения
относительно t
и подстановки значения С из уравнения
Из данного уравнения следует, что температура внутри стенки изменяется по кривой. Если коэффициент b отрицателен, то кривая направлена выпуклостью вниз; если b положителен, то выпуклостью вверх.
Из данного уравнения следует, что температура внутри стенки изменяется по кривой. Если коэффициент b отрицателен, то кривая направлена выпуклостью вниз; если b положителен, то выпуклостью вверх.
Слайд 152. Передача теплоты через многослойную плоскую стенку при граничных условиях I–го
рода
В тепловых аппаратах часто встречаются стенки, состоящие из нескольких плоских слоев различных материалов.
Выведем уравнение для этого случая.
Будем полагать, что все слои плотно прилегают друг к другу.
Слайд 16Выведем расчетную формулу теплопроводности сложной стенки при стационарном состоянии из уравнения
теплопроводности для отдельных слоев.
Тепловой поток, проходящий через любую изотермическую поверхность неоднородной стенки, один и тот же.
Тепловой поток, проходящий через любую изотермическую поверхность неоднородной стенки, один и тот же.
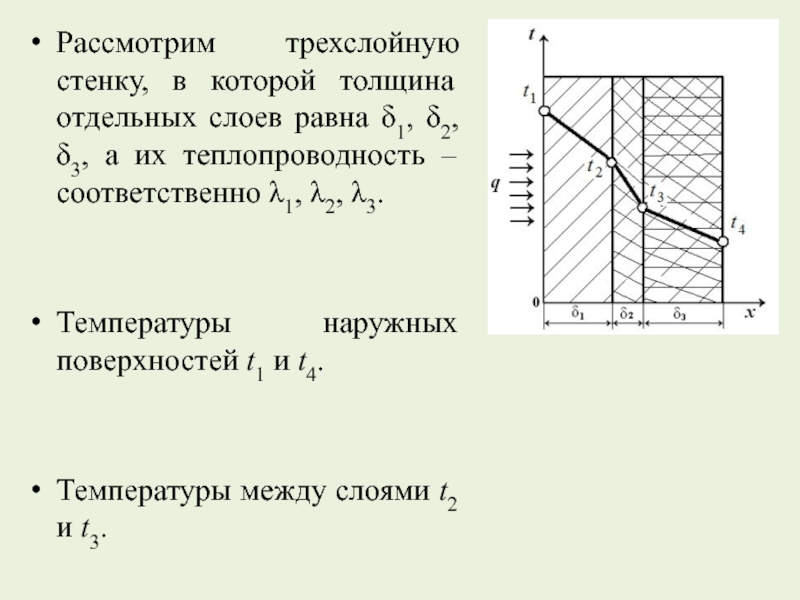
Слайд 17Рассмотрим трехслойную стенку, в которой толщина отдельных слоев равна δ1, δ2,
δ3, а их теплопроводность – соответственно λ1, λ2, λ3.
Температуры наружных поверхностей t1 и t4.
Температуры между слоями t2 и t3.
Температуры наружных поверхностей t1 и t4.
Температуры между слоями t2 и t3.
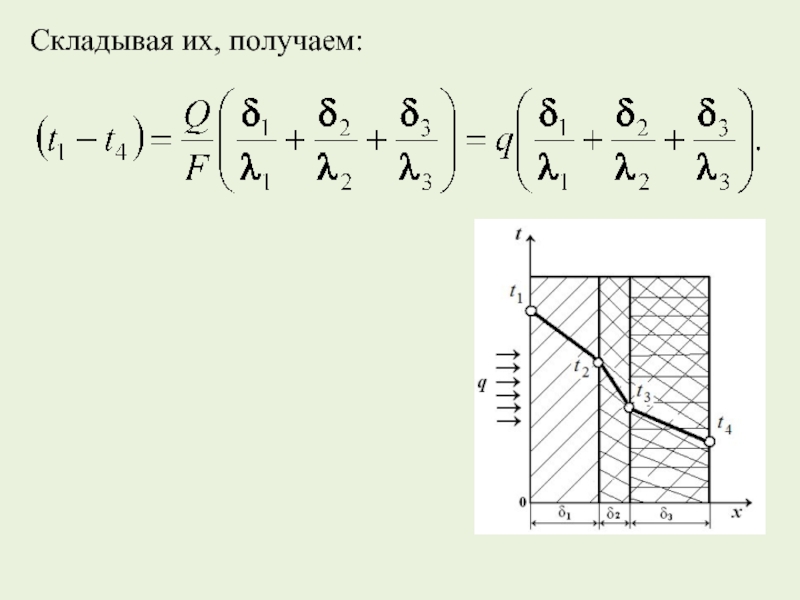
Слайд 20Преобразуем полученное равенство.
Получим формулы определяющие тепловой поток и мощность (удельный) теплового
потока:
Слайд 21где Δt – температурный перепад, т.е. разность температур наружных поверхностей стенки;
R
= R1 + R2 + R3 – общее термическое сопротивление многослойной стенки, равное сумме термических сопротивлений отдельных слоев стенки.
Слайд 22
– термическое сопротивление слоя;
– полное термическое сопротивление многослойной плоской стенки.
Слайд 23Температуры (°С) между отдельными слоями сложной стенки находим из следующих уравнений:
Температура
в каждом слое стенки при постоянной теплопроводности изменяется по линейному закону, а для многослойной стенки температурный график представляет собой ломаную линию.
Слайд 243. Передача теплоты через однослойную цилиндрическую стенку при граничных условиях I–го
рода
Слайд 25t1 и t2 – постоянные температуры внутренней и внешней поверхностей прямой
цилиндрической трубы.
Изотермические поверхности будут цилиндрическими поверхностями, имеющими общую ось с трубой.
Температура меняется только в направлении радиуса, благодаря этому и поток теплоты тоже будет радиальным.
Труба имеет бесконечную длину.
Изотермические поверхности будут цилиндрическими поверхностями, имеющими общую ось с трубой.
Температура меняется только в направлении радиуса, благодаря этому и поток теплоты тоже будет радиальным.
Труба имеет бесконечную длину.
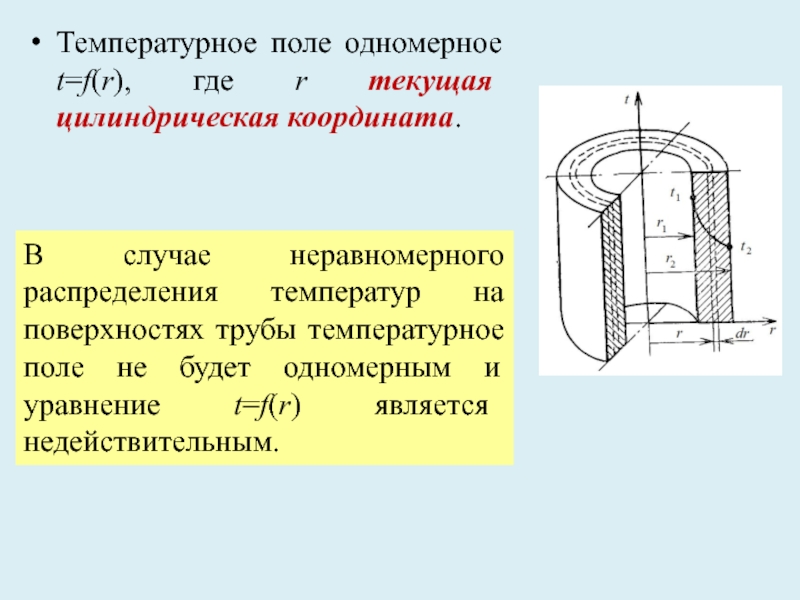
Слайд 26Температурное поле одномерное t=f(r), где r текущая цилиндрическая координата.
В случае неравномерного
распределения температур на поверхностях трубы температурное поле не будет одномерным и уравнение t=f(r) является недействительным.
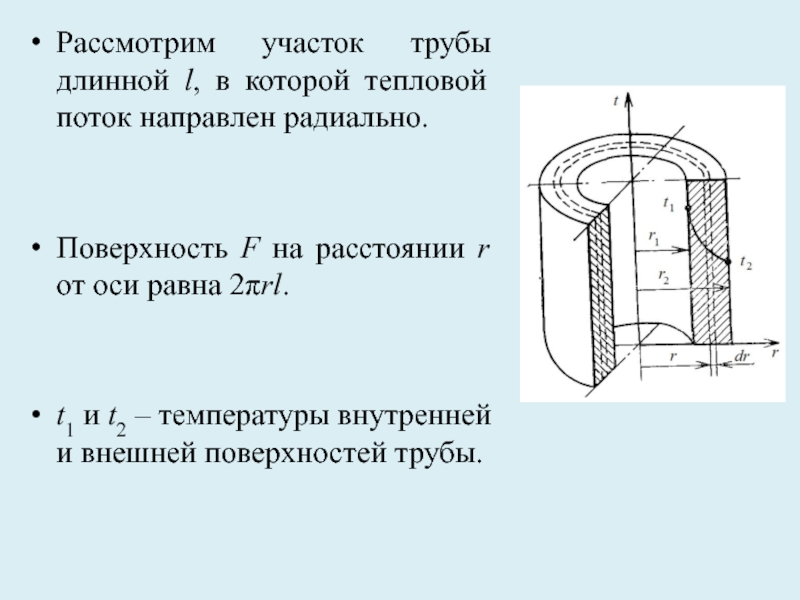
Слайд 27Рассмотрим участок трубы длинной l, в которой тепловой поток направлен радиально.
Поверхность
F на расстоянии r от оси равна 2πrl.
t1 и t2 – температуры внутренней и внешней поверхностей трубы.
t1 и t2 – температуры внутренней и внешней поверхностей трубы.
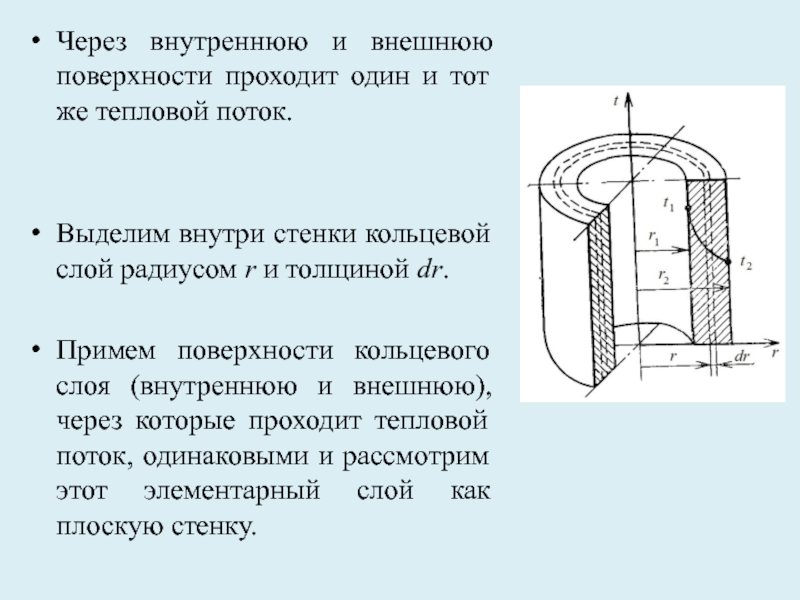
Слайд 28Через внутреннюю и внешнюю поверхности проходит один и тот же тепловой
поток.
Выделим внутри стенки кольцевой слой радиусом r и толщиной dr.
Примем поверхности кольцевого слоя (внутреннюю и внешнюю), через которые проходит тепловой поток, одинаковыми и рассмотрим этот элементарный слой как плоскую стенку.
Выделим внутри стенки кольцевой слой радиусом r и толщиной dr.
Примем поверхности кольцевого слоя (внутреннюю и внешнюю), через которые проходит тепловой поток, одинаковыми и рассмотрим этот элементарный слой как плоскую стенку.
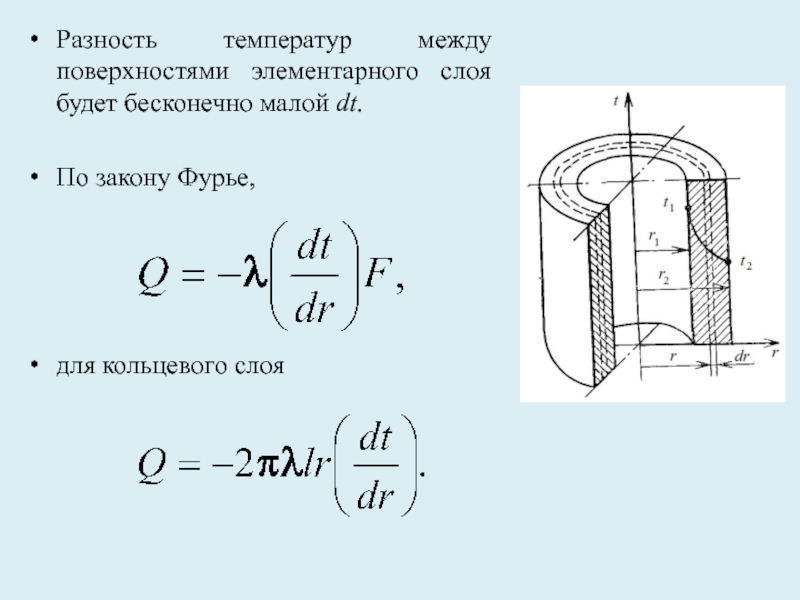
Слайд 29Разность температур между поверхностями элементарного слоя будет бесконечно малой dt.
По закону
Фурье,
для кольцевого слоя
для кольцевого слоя
Слайд 30Разделяя переменные, получаем
Интегрируя полученное уравнение в пределах от t1 до t2
и от r1 до r2 и при λ=const, получаем
Слайд 31Выразим тепловой поток
Выводы из полученного уравнения:
Распределение температур в стенке цилиндрической трубы
представляет собой логарифмическую кривую.
Тепловой поток, проходящий через цилиндрическую стенку, определяется заданными граничными условиями и зависит от отношения наружного диаметра к внутреннему.
Тепловой поток, проходящий через цилиндрическую стенку, определяется заданными граничными условиями и зависит от отношения наружного диаметра к внутреннему.
Слайд 32Тепловой поток может быть отнесен к единице длины трубы ql и
к 1 м2 внутренней или внешней поверхности q1 и q2.
Расчетные формулы принимают следующий вид:
Расчетные формулы принимают следующий вид:
Слайд 334. Передача теплоты через многослойную цилиндрическую стенку при граничных условиях I–го
рода
Слайд 34Цилиндрическая стенка состоит из трех плотно прилегающих слоев.
Температура внутренней поверхности стенки
t1, наружной t4.
Температуры между слоями t2 и t3.
Температуры между слоями t2 и t3.
Слайд 35Теплопроводность слоев равны λ1, λ2, λ3.
Диаметры слоев равны d1, d2,
d3, d4.
Температура каждого слоя стенки изменяется по логарифмической кривой.
Общая температурная кривая представляет собой ломаную логарифмическую кривую.
Температура каждого слоя стенки изменяется по логарифмической кривой.
Общая температурная кривая представляет собой ломаную логарифмическую кривую.
Слайд 36При стационарном режиме через все слои проходит один и тот же
тепловой поток.
Для каждого слоя тепловой поток равен:
Для каждого слоя тепловой поток равен:
Слайд 37Решая полученные уравнения относительно разности температур и почленно складывая, получаем
откуда
Слайд 40Постоянный тепловой поток направлен через шаровую стенку.
Источник теплоты находится внутри шара.
Температура
изменяется только по направлению радиуса.
Изотермические поверхности представляют собой концентрические шаровые поверхности.
Температура внутренней поверхности стенки t1, наружной t2.
Теплопроводность стенки λ постоянна.
Внутренний радиус шара r1, наружный r2.
Изотермические поверхности представляют собой концентрические шаровые поверхности.
Температура внутренней поверхности стенки t1, наружной t2.
Теплопроводность стенки λ постоянна.
Внутренний радиус шара r1, наружный r2.
Слайд 41Тепловой поток, проходящий через шаровой слой радиусом r и толщиной dr,
находим из уравнения Фурье:
или
или
Слайд 42
Интегрируя данное уравнение по t и r.
Постоянную интегрирования определяем из граничных
условий
при r = r1, то t = t1,
при r = r2, то t = t2, получаем
при r = r1, то t = t1,
при r = r2, то t = t2, получаем
