- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Тепломассообмен. Система дифференциальных уравнений конвективного теплообмена. Условия однозначности презентация
Содержание
- 1. Тепломассообмен. Система дифференциальных уравнений конвективного теплообмена. Условия однозначности
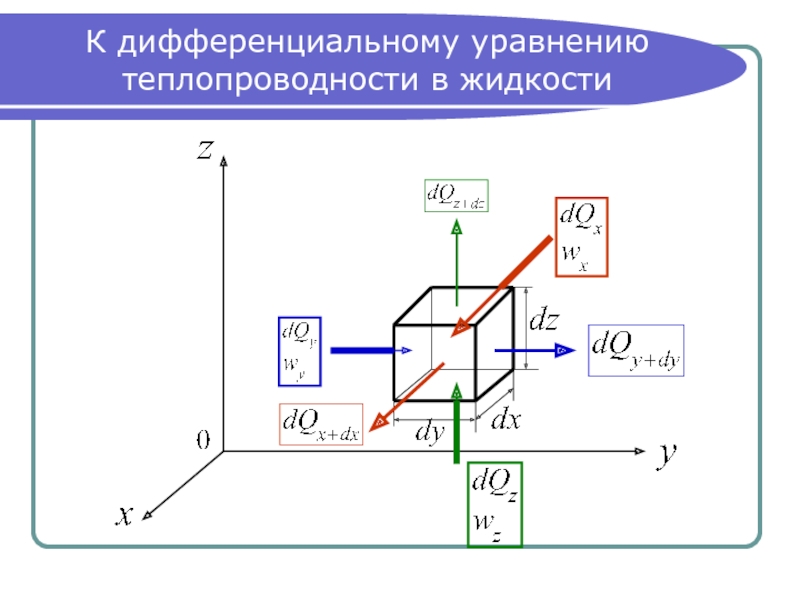
- 2. К дифференциальному уравнению теплопроводности в жидкости
- 3. Уравнение теплового баланса
- 4. Ряд Тейлора
- 5. Теплота, подведенная теплопроводностью и конвекцией
- 6. Теплота, подведенная к элементарному объему
- 7. Общий вид дифференциального уравнения энергии Фурье-Кирхгофа
- 8. Развернутое выражение дифференциального уравнения энергии
- 9. Дифференциальное уравнение энергии Фурье-Кирхгофа
- 10. Дифференциальное уравнение движения жидкости Навье-Стокса
- 11. Продольное обтекание жидкостью вертикальной пластины
- 12. Проекции дифференциального уравнения движения на оси координат
- 13. Составляющие проекций уравнения движения на оси
- 14. Система дифференциальных уравнений конвективного теплообмена
- 15. Условия однозначности ● Геометрические
- 16. Общие решения задачи конвективного теплообмена
Слайд 1Тепломассообмен 10
● Система дифференциальных уравнений конвективного теплообмена
● Условия однозначности
Слайд 3Уравнение теплового баланса
В математической физике изучают явление в бесконечно
малом объеме
dv за бесконечно малый промежуток времени
что позволяет пренебречь величинами 2 порядка малости.
Принимаются допущения: тело однородно и изотропно;
физические свойства тела в малом объеме dv постоянны;
внутренние источники теплоты отсутствуют.
По аналогии с дифференциальным уравнением теплопровод-
ности в твердом теле, которое было выведено ранее, можно
получить дифференциальное уравнение теплопроводности
в жидкости (уравнение энергии Фурье – Кирхгофа).
Уравнение теплового баланса: (1)
где Q – изменение внутренней энергии объема dv за время :
что позволяет пренебречь величинами 2 порядка малости.
Принимаются допущения: тело однородно и изотропно;
физические свойства тела в малом объеме dv постоянны;
внутренние источники теплоты отсутствуют.
По аналогии с дифференциальным уравнением теплопровод-
ности в твердом теле, которое было выведено ранее, можно
получить дифференциальное уравнение теплопроводности
в жидкости (уравнение энергии Фурье – Кирхгофа).
Уравнение теплового баланса: (1)
где Q – изменение внутренней энергии объема dv за время :
Слайд 4Ряд Тейлора
(2) - изменение внутренней энергии
объема dv за
время ;
теплота, подведенная (3)
конвекцией и теплопроводностью (4)
к объему dv за время .
Теплота на входе вдоль оси х: (5)
Теплота на выходе вдоль оси х: (6)
Если функция в интервале dx непрерывна и
дифференцируема, то ее можно разложить в ряд Тейлора:
(7)
где как величина 2 порядка малости.
теплота, подведенная (3)
конвекцией и теплопроводностью (4)
к объему dv за время .
Теплота на входе вдоль оси х: (5)
Теплота на выходе вдоль оси х: (6)
Если функция в интервале dx непрерывна и
дифференцируема, то ее можно разложить в ряд Тейлора:
(7)
где как величина 2 порядка малости.
Слайд 5Теплота, подведенная теплопроводностью и конвекцией
Подставляя (5), (6), (7) в (4),
имеем теплоту, подведенную
вдоль оси х к бесконечно малому объему dv за бесконечно
малый промежуток времени
(8)
Аналогично (9)
вдоль осей y и z:
(10)
После подстановки (2), (3), (8), (9), (10) в (1) получаем:
вдоль оси х к бесконечно малому объему dv за бесконечно
малый промежуток времени
(8)
Аналогично (9)
вдоль осей y и z:
(10)
После подстановки (2), (3), (8), (9), (10) в (1) получаем:
Слайд 6Теплота, подведенная
к элементарному объему
После сокращения на dv,
имеем: (11)
где
Тогда теплота, подведенная к объему dv за время
конвекцией и теплопроводностью: (12)
где расход массы через единицу сечения
в единицу времени, кг/(м2с).
Аналогично вдоль оси y ;
и вдоль оси z: .
где
Тогда теплота, подведенная к объему dv за время
конвекцией и теплопроводностью: (12)
где расход массы через единицу сечения
в единицу времени, кг/(м2с).
Аналогично вдоль оси y ;
и вдоль оси z: .
Слайд 7Общий вид дифференциального уравнения энергии Фурье-Кирхгофа
Возьмем производные (13)
по координатам
х, y, z
от тепловых потоков: (14)
(15)
После подстановки (13), (14), (15) в (11) получим общий
вид дифференциального уравнения энергии Фурье-Кирхгофа:
(16)
от тепловых потоков: (14)
(15)
После подстановки (13), (14), (15) в (11) получим общий
вид дифференциального уравнения энергии Фурье-Кирхгофа:
(16)
Слайд 8Развернутое выражение дифференциального уравнения энергии
В уравнении (16) выражение
(17)
представляет собой дифференциальное уравнение
сплошности (неразрывности) течения жидкости.
Введем также обозначение
оператора Лапласа: . (18)
С учетом выражений (17) и (18) уравнение энергии
примет вид: (19)
где энтальпия h = cpt, тогда развернутое уравнение энергии:
(20)
представляет собой дифференциальное уравнение
сплошности (неразрывности) течения жидкости.
Введем также обозначение
оператора Лапласа: . (18)
С учетом выражений (17) и (18) уравнение энергии
примет вид: (19)
где энтальпия h = cpt, тогда развернутое уравнение энергии:
(20)
Слайд 9Дифференциальное
уравнение энергии Фурье-Кирхгофа
В уравнении (20) выражение в скобках представляет
собой
полную (субстанциональную) производную от температуры
по времени и координатам: (21)
где проекции скоростей
жидкости на оси координат:
После деления уравнения (20) на ,
с учетом (21) и обозначения коэффициента
температуропроводности жидкости:
получаем окончательное выражение
дифференциального уравнения энергии: (22)
полную (субстанциональную) производную от температуры
по времени и координатам: (21)
где проекции скоростей
жидкости на оси координат:
После деления уравнения (20) на ,
с учетом (21) и обозначения коэффициента
температуропроводности жидкости:
получаем окончательное выражение
дифференциального уравнения энергии: (22)
Слайд 10Дифференциальное уравнение
движения жидкости Навье-Стокса
Частным случаем дифференциального уравнения энергии
(22)
для твердого тела является
дифференциальное уравнение тепло-
проводности, которое было выведено ранее: .
Вывод дифференциального уравнения движения жидкости
Навье-Стокса сложен, поэтому
оно приводится без вывода: (1)
где оператор Гамильтона
для давления:
Стрелки в уравнении (1) отмечают векторные величины.
дифференциальное уравнение тепло-
проводности, которое было выведено ранее: .
Вывод дифференциального уравнения движения жидкости
Навье-Стокса сложен, поэтому
оно приводится без вывода: (1)
где оператор Гамильтона
для давления:
Стрелки в уравнении (1) отмечают векторные величины.
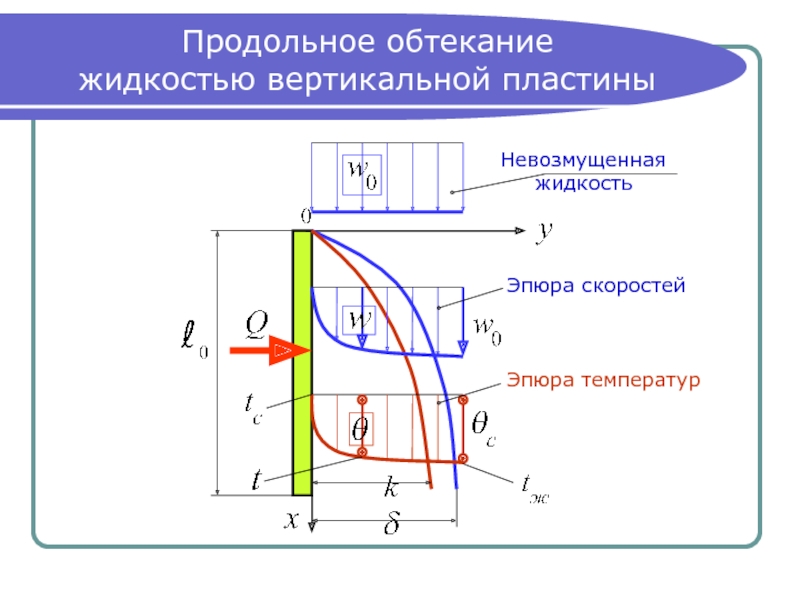
Слайд 11Продольное обтекание
жидкостью вертикальной пластины
Невозмущенная
жидкость
Эпюра скоростей
Эпюра температур
Слайд 12Проекции дифференциального уравнения движения на оси координат
При продольном обтекании вертикальной
пластины, когда ось
«х» направлена вниз, проекции ускорения на оси координат:
, тогда - ускорение свободного
падения.
В этом случае проекции
уравнения Навье-Стокса (1) (2)
на оси координат:
(3)
(4)
«х» направлена вниз, проекции ускорения на оси координат:
, тогда - ускорение свободного
падения.
В этом случае проекции
уравнения Навье-Стокса (1) (2)
на оси координат:
(3)
(4)
Слайд 13Составляющие проекций
уравнения движения на оси координат
В левых частях уравнений
(2), (3), (4) находятся полные
(субстанциональные) производные от скоростей по времени
и координатам:
Введем обозначения
операторов Лапласа:
(субстанциональные) производные от скоростей по времени
и координатам:
Введем обозначения
операторов Лапласа:
Слайд 14Система дифференциальных уравнений конвективного теплообмена
Дифференциальное уравнение сплошности (неразрывности):
или в
(5) векторной форме: (6)
Итак конвективный теплообмен описывается системой
дифференциальных уравнений: (7)
Чтобы из бесконечного
множества процессов,
описываемых системой
уравнений (7), выделить
конкретный процесс,
надо добавить условия
однозначности.
(5) векторной форме: (6)
Итак конвективный теплообмен описывается системой
дифференциальных уравнений: (7)
Чтобы из бесконечного
множества процессов,
описываемых системой
уравнений (7), выделить
конкретный процесс,
надо добавить условия
однозначности.
Слайд 15Условия однозначности
● Геометрические условия: вертикальная плоскость длиной
● Физические условия: величины постоянные,
берутся при определяющей температуре. Чаще всего ей
является средняя температура жидкости .
● Начальные условия: при
● Граничные условия I рода: при
(8)
В системе дифференциальных уравнений и условиях
однозначности есть три вида величин: независимые перемен-
ные - постоянные величины -
зависимые переменные -
Слайд 16Общие решения задачи
конвективного теплообмена
Шесть неизвестных (независимых величин) могут быть
найдены при наличии шести уравнений. С учетом того, что
уравнение Навье-Стокса в проекциях на оси координат дает
три дифференциальных уравнения, общие решения системы
уравнений (7) с граничными условиями (8):
(9)