- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теория электромагнитного поля презентация
Содержание
- 1. Теория электромагнитного поля
- 2. 1. Электрическое поле. Его основные характеристики.
- 3. Опыт показал, что между наэлектризованными телами
- 4. Электрический заряд обозначается буквой q, единица
- 5. Наименьшей по массе устойчивой частицей, имеющей
- 6. Суммарный заряд электрически изолированной системы не
- 7. Силы электростатического взаимодействия заряженных тел
- 8. Закон Кулона. Сила взаимодействия двух неподвижных
- 9. где
- 11. Сам по себе закон Кулона не
- 12. Согласно этой теории вокруг каждого
- 13. Определение: Электрическое поле есть особый вид
- 14. Силовой характеристикой электрического поля служит вектор
- 15. Напряженность поля, создаваемого точечным зарядом:
- 17. Однородным называют электрическое поле, векторы напряженности
- 18. Для графического изображения электростатического поля в
- 19. Следует помнить, что: 1) силовые
- 21. Принцип суперпозиции электрических полей: напряженность электрического
- 23. Помимо силовой характеристики электрического поля существует
- 24. Существуют два вида электрических полей: а) потенциальное ЭП; б) вихревое ЭП.
- 25. Потенциальное ЭП – это электростатическое поле,
- 26. Потенциал электрического поля – скалярная физическая
- 27. Другими словами, потенциал электрического поля в
- 28. Разность потенциалов – величина, равная работе
- 29. Работа электростатического поля при перемещении
- 30. Работа электростатического поля не зависит от
- 31. Такое поле называется потенциальным. Электростатическое поле – потенциальное поле.
- 32. Кроме потенциальных ЭП, существуют также вихревые
- 33. Связь между разностью потенциалов и напряженностью ЭП
- 34. Напряженность однородного поля численно
- 35. Воображаемую поверхность, все точки которой имеют
- 36. Потенциал поля точечного заряда q на
- 38. Принцип суперпозиции электрических полей – потенциал
- 39. Электрическая емкость Электрическая емкость проводника C –
- 40. Электрическая емкость проводника определяется его формой,
- 41. Однако уединенные проводники обладают небольшой емкостью.
- 42. Плоский конденсатор – система из двух
- 43. Электроемкость конденсатора – отношение заряда одной
- 44. Конденсаторы различаются по форме (плоские,
- 45. Формулы для вычисления емкости конденсаторов:
- 46. Энергия электрического поля Электрическое
- 47. Объемная плотность энергии электростатического поля ω
- 48. Энергия плоского конденсатора. Исходя из
- 49. 2. Магнитное поле и его характеристики
- 50. Таким образом, источниками магнитного поля являются
- 51. Определение: Магнитное поле есть особый вид
- 52. Для описания магнитного поля необходимо
- 53. За положительное направление вектора B принимается
- 54. Таким образом, исследуя магнитное поле, создаваемое
- 55. Аналогично силовым линиям в электростатике можно
- 57. Для того чтобы количественно описать магнитное
- 58. Здесь q – величина заряда,
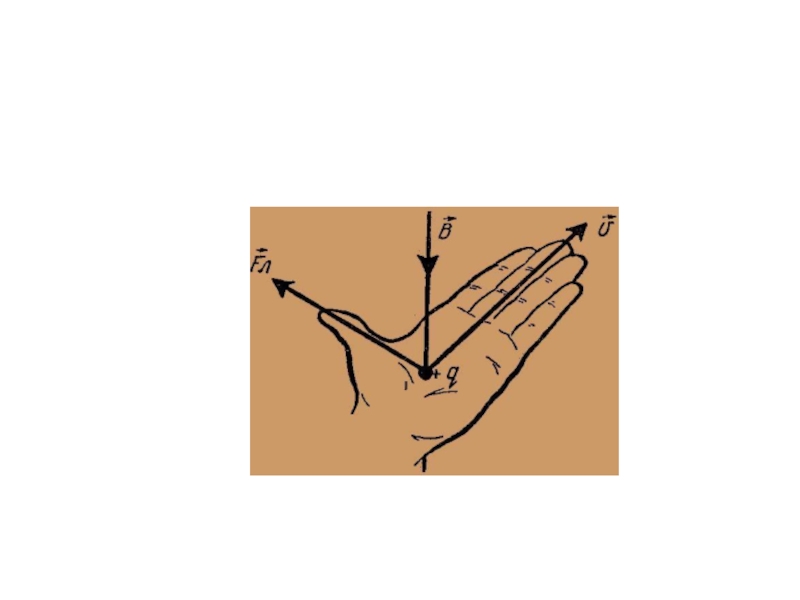
- 59. Направление силы Лоренца определяют по правилу левой руки:
- 61. Сила Лоренца (магнитная сила) всегда перпендикулярна
- 62. Из формулы Лоренца можно дать определение
- 63. Единицей магнитной индукции В является тесла
- 64. где μ – относительная магнитная
- 65. Действие магнитного поля на проводник с
- 66. Сила, действующая в этом случае на
- 67. Из курса элементарной физики известно, что
- 68. Эта сила называется силой Ампера.
- 69. Одним из важных примеров магнитного
- 70. Если по двум параллельным проводникам электрические
- 72. Опыты показали, что модуль силы, действующей
- 73. Закон Био-Савара-Лапласа Позволяет вычислить напряженность магнитного поля,
- 74. П.С. Лаплас проанализировал полученные данные и
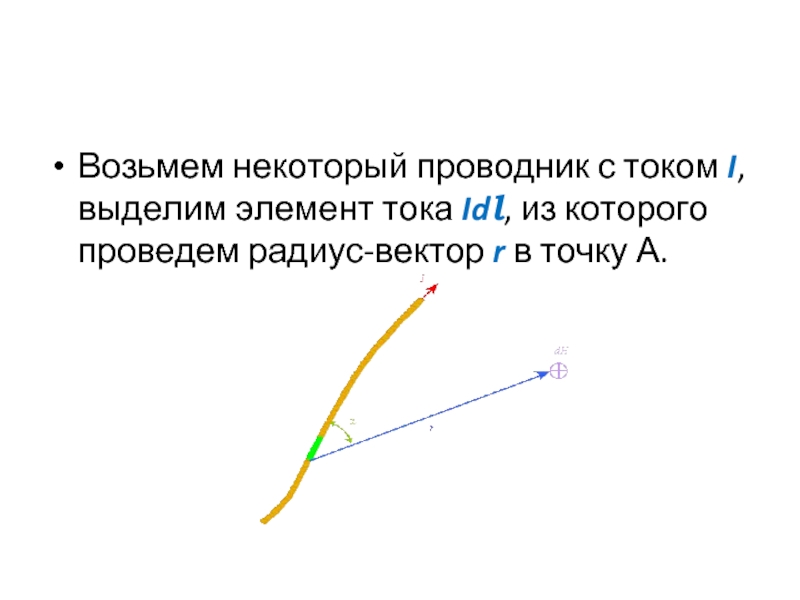
- 75. Возьмем некоторый проводник с током I,
- 76. В точке А элемент тока создает
- 77. k – коэффициент пропорциональности, зависящий от
- 78. Интегрируя эту формулу, находим напряженность поля, создаваемого током любой формы:
- 79. Так, напряженность магнитного поля в центре
- 80. Напряженность магнитного поля, созданного бесконечным прямолинейным
- 81. Напряженность магнитного поля соленоида (однородного):
- 82. Энергия магнитного поля Поскольку магнитное поле является
Слайд 1ВОЕННО–МЕДИЦИНСКАЯ АКАДЕМИЯ
имени С.М. Кирова
Кафедра биологической и медицинской физики
ЛЕКЦИЯ № 9
по дисциплине
на тему: «Основы теории электромагнитного поля»
для курсантов и студентов I курса по специальности «Лечебное дело»
Слайд 2
1. Электрическое поле. Его основные характеристики. Потенциальное и вихревое электрические поля.
Все
Наличие электрического заряда проявляется в том, что заряженное тело взаимодействует с другими заряженными телами.
Слайд 3
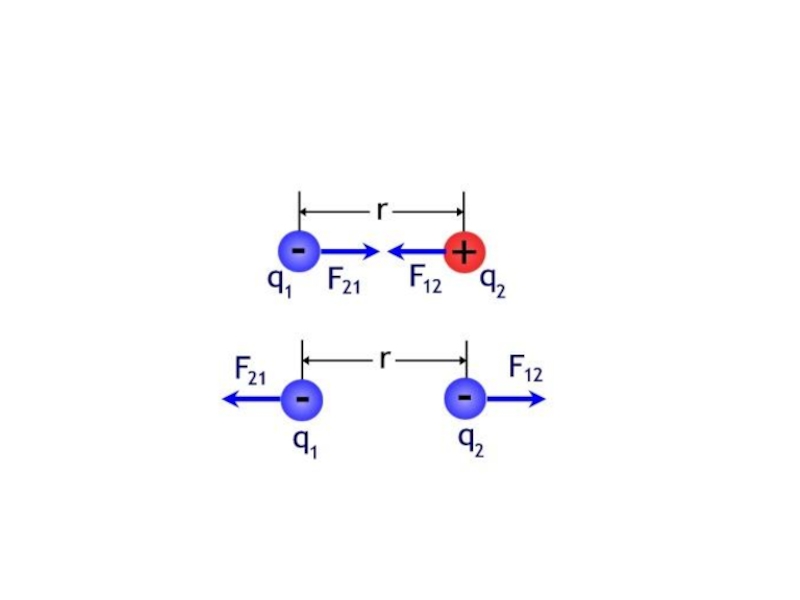
Опыт показал, что между наэлектризованными телами имеется либо притяжение, либо отталкивание.
Это объясняется тем, что имеется два вида электрических зарядов, условно называемых положительными и отрицательными.
Одноименные заряды отталкиваются, разноименные – притягиваются.
Слайд 4
Электрический заряд обозначается буквой q, единица измерения заряда – кулон (Кл).
Электрический
Элементарный заряд - это наименьший встречающийся в природе электрический заряд, равный 1,6·10-19 Кл.
Слайд 5
Наименьшей по массе устойчивой частицей, имеющей отрицательный элементарный заряд, является электрон
У электрона существует и античастица, имеющая положительный элементарный заряд – позитрон.
Слайд 6
Суммарный заряд электрически изолированной системы не изменяется при любых процессах, происходящих
q = q1 + q2 + q3 +…+ qn = const
Слайд 7
Силы электростатического взаимодействия заряженных тел подчиняются закону Кулона, поэтому их часто
Слайд 8
Закон Кулона. Сила взаимодействия двух неподвижных точечных зарядов прямо пропорциональна величине
Слайд 9
где
– коэффициент пропорциональности, или константа Кулона,
ε – относительная диэлектрическая проницаемость среды.
Сила направлена вдоль прямой, соединяющей заряженные тела.
Слайд 11
Сам по себе закон Кулона не дает представления о том, каков
Слайд 12
Согласно этой теории вокруг каждого заряда существует электрическое поле.
Взаимодействие электрических
Слайд 13
Определение:
Электрическое поле есть особый вид материи, посредством которого осуществляются силовые воздействия
Слайд 14
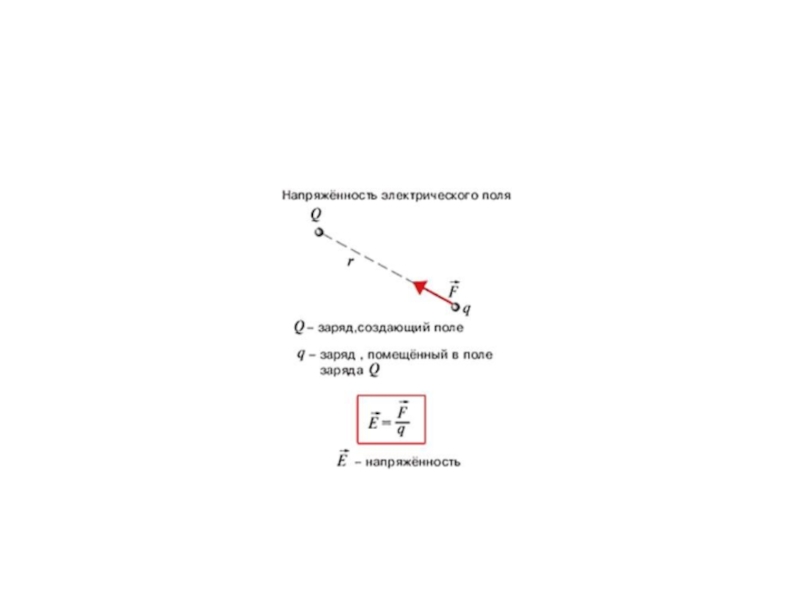
Силовой характеристикой электрического поля служит вектор напряженности электрического поля.
Он численно
Размерность напряженности ЭП: Н/Кл.
Слайд 15
Напряженность поля, создаваемого точечным зарядом:
,
где r – расстояние от заряда
Слайд 17
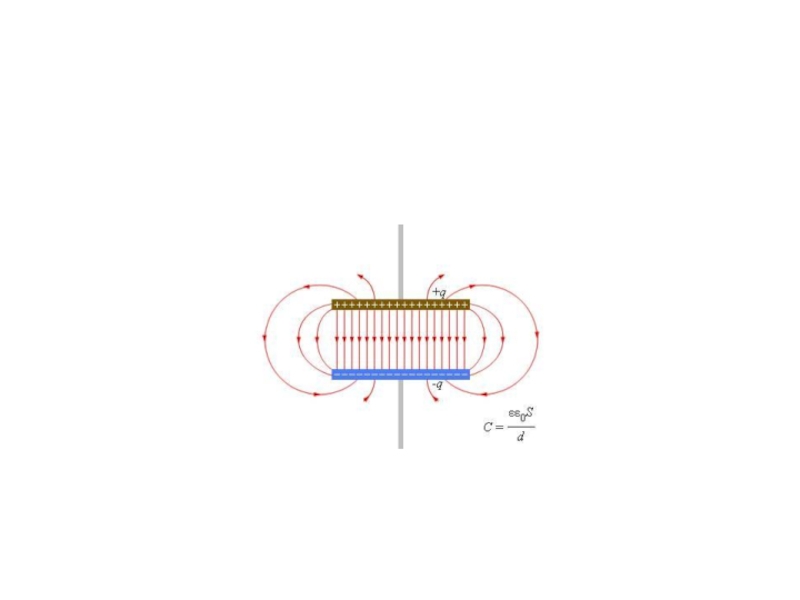
Однородным называют электрическое поле, векторы напряженности которого одинаковы во всех точках
Приблизительно однородным является электрическое поле между двумя разноименно заряженными металлическими пластинами, расположенными параллельно друг другу.
Слайд 18
Для графического изображения электростатического поля в пространстве применяется метод силовых линий,
Силовыми линиями называются линии, касательные к которым в каждой точке совпадают с направлением вектора напряженности в этой точке.
Слайд 19
Следует помнить, что:
1) силовые линии электростатического поля не пересекаются друг
2) имеют начало на положительном заряде и конец на отрицательном или уходят на бесконечность, т.е. являются незамкнутыми;
3) густота силовых линий пропорциональна величине напряженности электростатического поля.
Слайд 21
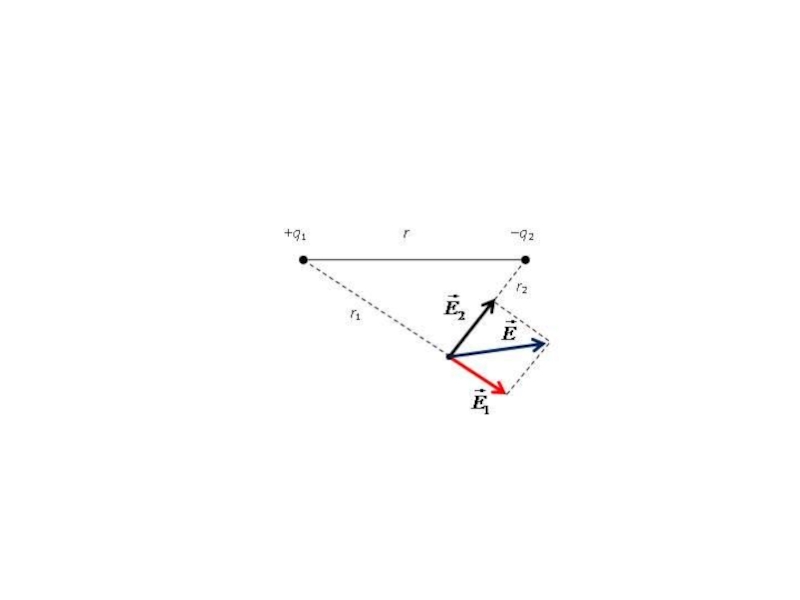
Принцип суперпозиции электрических полей: напряженность электрического поля системы точечных зарядов равна
или
Слайд 23
Помимо силовой характеристики электрического поля существует и характеристика его источников -
D = ε0εE [Кл.м-2]
Слайд 25
Потенциальное ЭП – это электростатическое поле, т.е. поле, созданное системой неподвижных
Важной характеристикой потенциального ЭП является потенциал электрического поля (электрический потенциал).
Это энергетическая характеристика потенциального ЭП.
Слайд 26
Потенциал электрического поля – скалярная физическая величина, численно равная отношению потенциальной
Единица измерения: 1 вольт (В) = 1 Дж/Кл.
Слайд 27
Другими словами, потенциал электрического поля в данной точке равен работе сторонних
Слайд 28
Разность потенциалов – величина, равная работе А1,2 , которую совершают силы
Слайд 29
Работа электростатического поля при перемещении заряда q из точки с потенциалом
А1,2 = q·(ϕ1 - ϕ2)
Слайд 30
Работа электростатического поля не зависит от вида траектории перемещения заряда, а
Соответственно, при перемещении заряда по замкнутому контуру полная работа электростатического поля равна нулю.
Слайд 32
Кроме потенциальных ЭП, существуют также вихревые электрические поля.
Их силовые линии
Источником вихревых ЭП является переменное магнитное поле.
Слайд 33Связь между разностью потенциалов и напряженностью ЭП
Между напряженностью ЭП и потенциалом
или
Слайд 34
Напряженность однородного поля численно равна разности потенциалов на единице длины линии
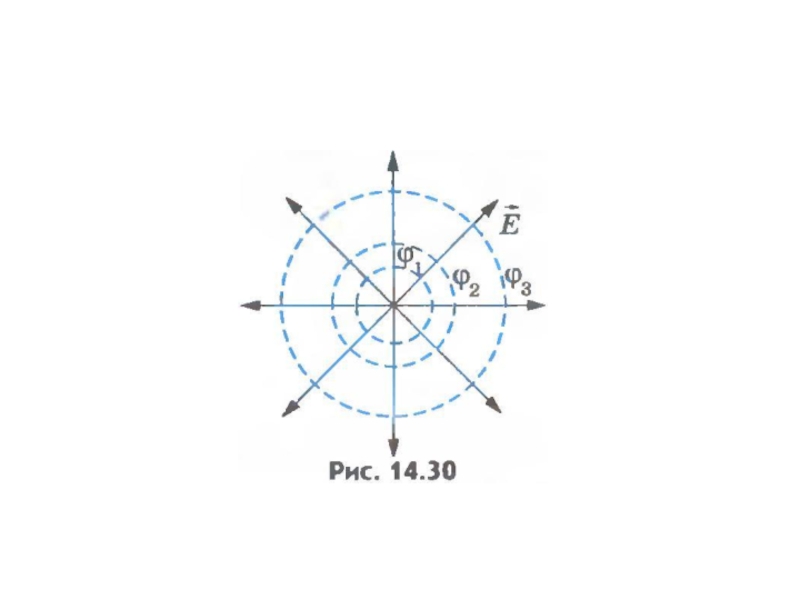
Слайд 35
Воображаемую поверхность, все точки которой имеют одинаковый потенциал, называют эквипотенциальной поверхностью.
Силовые линии и эквипотенциальные поверхности взаимно перпендикулярны.
При перемещении заряда по эквипотенциальной поверхности работа не совершается.
Слайд 36
Потенциал поля точечного заряда q на расстоянии r от него:
Эквипотенциальная поверхность
Слайд 38
Принцип суперпозиции электрических полей – потенциал поля системы точечных зарядов φ
Слайд 39Электрическая емкость
Электрическая емкость проводника C – количественная мера его способности удерживать
Электрическая емкость уединенного проводника равна отношению заряда проводника q к его потенциалу φ :
[1 Кл/В = 1 Ф]
Слайд 40
Электрическая емкость проводника определяется его формой, геометрическими размерами и свойствами окружающей
Емкость уединенного шара, погруженного в однородный безграничный диэлектрик с проницаемостью ε, равна
Слайд 41
Однако уединенные проводники обладают небольшой емкостью.
Для накопления большого по величине
Конденсатором называют устройство из двух проводников (обкладок), разделенных слоем диэлектрика, толщина которого мала по сравнению с размерами проводников.
Слайд 42
Плоский конденсатор – система из двух плоских параллельных металлических пластин, расположенных
Слайд 43
Электроемкость конденсатора – отношение заряда одной из его обкладок к разности
,
где φ1 и φ2 – потенциалы пластин,
U – напряжение на конденсаторе.
Слайд 44
Конденсаторы различаются по форме (плоские, сферические, цилиндрические), а также по материалу,
Слайд 46
Энергия электрического поля
Электрическое поле является носителем энергии.
В общем случае количественной
Слайд 47
Объемная плотность энергии электростатического поля ω – физическая величина, равная отношению
Слайд 48
Энергия плоского конденсатора.
Исходя из величины работы А, совершаемой электрическим полем при
получим формулу для энергии заряженного конденсатора:
Слайд 492. Магнитное поле и его характеристики
Магнитные явления были известны человечеству
Впоследствии выяснилось, что в пространстве вокруг движущихся заряженных тел, движущихся заряженных частиц, а также вокруг проводников, по которым текут постоянные токи, возникает особого вида поле, называемое магнитным полем.
Слайд 50
Таким образом, источниками магнитного поля являются движущиеся электрические заряды (следовательно, и
Магнитное поле постоянных магнитов также создается электрическими микротоками, циркулирующими внутри молекул вещества (гипотеза Ампера).
Слайд 51
Определение: Магнитное поле есть особый вид материи, посредством которого осуществляются силовые
Слайд 52
Для описания магнитного поля необходимо ввести силовую характеристику поля, аналогичную вектору
Слайд 53
За положительное направление вектора B принимается направление от южного полюса S
Слайд 54
Таким образом, исследуя магнитное поле, создаваемое током или постоянным магнитом, с
Такое исследование позволяет представить пространственную структуру магнитного поля.
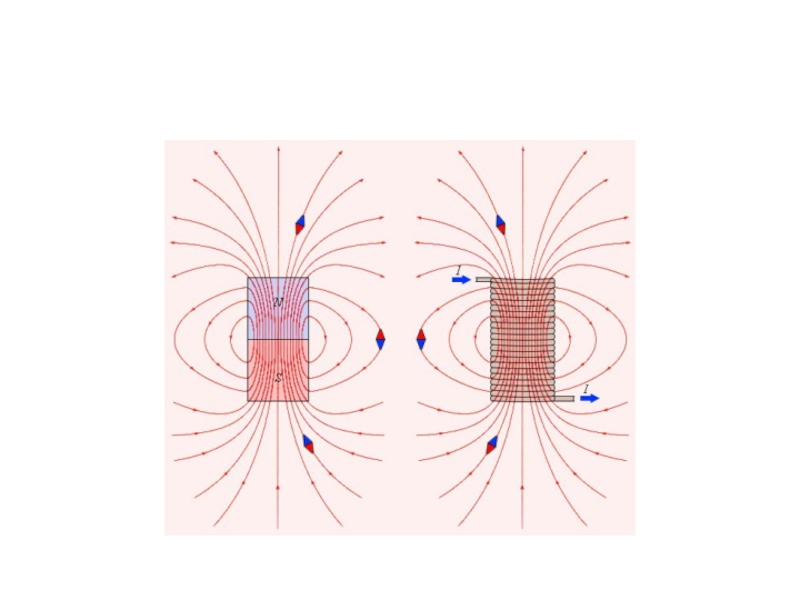
Слайд 55
Аналогично силовым линиям в электростатике можно построить линии магнитной индукции, в
Линии магнитной индукции всегда замкнуты, они нигде не обрываются. Поэтому магнитное поле является вихревым силовым полем.
Слайд 57
Для того чтобы количественно описать магнитное поле, нужно указать способ определения
Известно, что на заряд, движущийся в магнитном поле, действует сила Лоренца, численно равная:
Слайд 58
Здесь
q – величина заряда,
v – его скорость,
В – величина
α – угол между векторами v и В.
Слайд 61
Сила Лоренца (магнитная сила) всегда перпендикулярна плоскости, в которой лежат векторы
Этим она отличается от электрической силы, которая направлена так же, как вектор Е.
Слайд 62
Из формулы Лоренца можно дать определение магнитной индукции В:
Вектор магнитной индукции
Слайд 63
Единицей магнитной индукции В является тесла (Тл).
Для характеристики магнитного поля источника
Слайд 64
где μ – относительная магнитная проницаемость среды, а μ0 – магнитная
Единица напряженности магнитного поля –
1 А·м-1.
Слайд 65
Действие магнитного поля на проводник с током. Закон Ампера.
А.М. Ампером было
Слайд 66
Сила, действующая в этом случае на участок проводника со стороны магнитного
Слайд 67
Из курса элементарной физики известно, что направление действия силы F определяется
Слайд 68
Эта сила называется силой Ампера.
Она достигает максимального по модулю значения
Слайд 69
Одним из важных примеров магнитного взаимодействия является взаимодействие параллельных токов.
Закономерности
Слайд 70
Если по двум параллельным проводникам электрические токи текут в одну и
В случае, когда токи текут в противоположных направлениях, проводники отталкиваются.
Взаимодействие токов вызывается их магнитными полями: магнитное поле одного тока действует силой Ампера на другой ток и наоборот.
Слайд 72
Опыты показали, что модуль силы, действующей на отрезок длиной Δl каждого
Слайд 73Закон Био-Савара-Лапласа
Позволяет вычислить напряженность магнитного поля, создаваемого постоянным током.
Ж.Б. Био и
Слайд 74
П.С. Лаплас проанализировал полученные данные и нашел, что напряженность магнитного поля
Слайд 75
Возьмем некоторый проводник с током I, выделим элемент тока Idl, из
Слайд 76
В точке А элемент тока создает магнитное поле, напряженность которого dH
Слайд 77
k – коэффициент пропорциональности, зависящий от выбора единиц.
В системе СИ
k = 1/(4π), поэтому:
Слайд 80
Напряженность магнитного поля, созданного бесконечным прямолинейным проводником с током в любой
Слайд 81
Напряженность магнитного поля соленоида (однородного):
где N – число витков; l –
Слайд 82Энергия магнитного поля
Поскольку магнитное поле является силовым полем, то оно обладает
Объемная плотность энергии магнитного поля вычисляется по формуле: