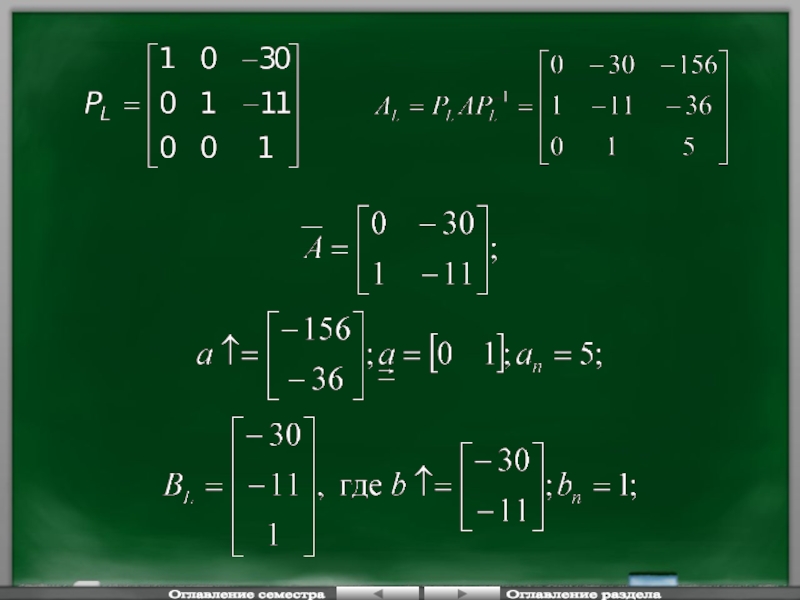- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теория автоматического управления. Современная ТАУ. (Часть 2) презентация
Содержание
- 1. Теория автоматического управления. Современная ТАУ. (Часть 2)
- 2. Учебный курс «Теория Автоматического Управления» Современная
- 3. Современная ТАУ Системы с обратной связью
- 4. Описание одномерных и многомерных объектов и систем
- 5. Связь матрично-векторной и вход-выходной моделей объектов и
- 6. Понятия управляемости и наблюдаемости Понятие управляемости
- 7. Понятия базиса в пространстве состояний Основные
- 8. Наблюдатели состояний Основные понятия и определения Оглавление семестра Редуцированный наблюдатель
- 9. Системы с обратной связью по состояниям
- 10. Управление и наблюдение в многомерных системах. Разделяющее
- 11. Закономерности движения Понятия возмущенного и невозмущенного
- 12. Оценка устойчивости состояния автоматических систем Понятие
- 13. Оценка устойчивости замкнутых систем с использованием функции
- 14. Математическое описание и исследование дискретно-непрерывных систем управления
- 15. Основные понятия и определения. Описание одномерных и
- 16. уравнение состояний уравнение наблюдений
- 17. В зависимости от соотношения степеней
- 18. Оглавление семестра Оглавление раздела
- 19. Пример Дан объект управления
- 20. 1) 2)
- 21. Алгоритм построения: Исходная математическая модель, представленная в
- 22. Пример: Дана структурная схема объекта управления Необходимо
- 23. Оглавление семестра Оглавление раздела
- 24. характеристическая матрица
- 25. Передаточная матрица – это матрица,
- 26. Основной задачей при построении
- 27. Пример 1) 2)
- 28. Оглавление семестра Оглавление раздела
- 29. 1. Можно ли, выбрав соответствующим образом входы
- 30. Оглавление семестра Оглавление раздела
- 31. Объект называется полностью наблюдаемым, если по данным измерения, наблюдения, на конечном интервале времени t0
- 32. Частично управляемый объект является стабилизируемым
- 33. Пример №1: - полная - неполная -
- 34. Пример №2: Определим управляемость и наблюдаемость:
- 35. Система всегда записана относительно некоторых
- 36. Поиск необходимого преобразования P может
- 37. Для исследования динамических систем в
- 38. 2) Транспонированная ОН (ТОН)
- 39. Для перехода к ней применяют преобразования (1)
- 40. Для перехода к данной форме
- 41. Динамический наблюдатель состояния (ДНС) –
- 42. Для синтеза наблюдателя необходимо ввести
- 43. В теории управления применяется 2
- 44. Для обеспечения асимптотического затухания ошибки
- 45. 2)
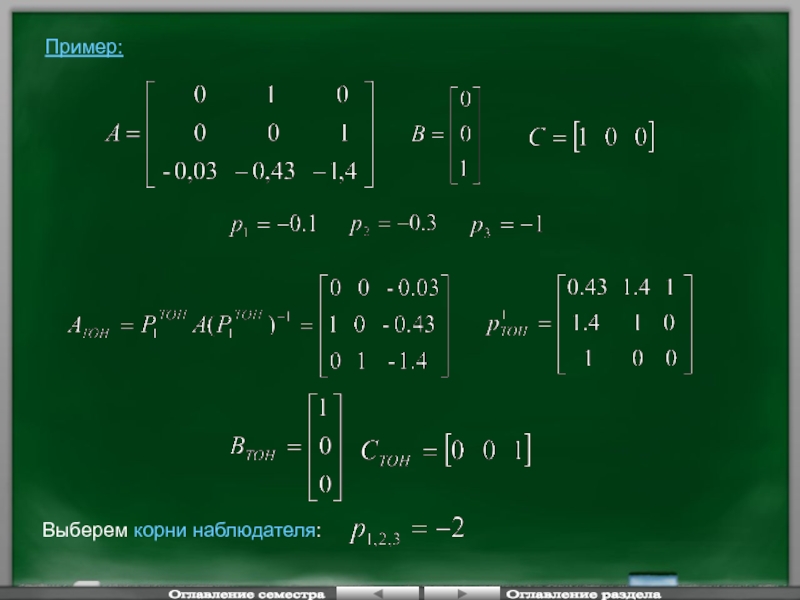
- 46. Пример: Выберем корни
- 47. Оглавление семестра Оглавление раздела
- 48. Оглавление семестра Оглавление раздела
- 49. Преимуществом использования ДНС при построении
- 50. Недостатком является его большая сложность при высокой
- 51. Редуцированный наблюдатель состояния. Для синтеза
- 52. Оглавление семестра Оглавление
- 53. Оглавление семестра
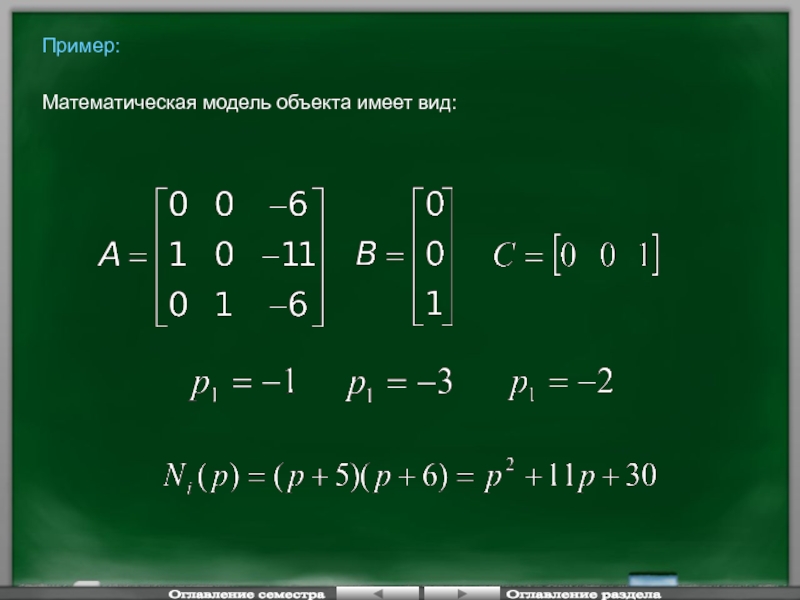
- 54. Пример: Математическая модель объекта имеет вид:
- 55. Оглавление семестра Оглавление раздела
- 56. Оглавление семестра Оглавление раздела
- 57. Недостатком наблюдателя Луенбергера по сравнению
- 58. Системы с обратной связью по состоянию Модальное
- 59. Модальное управление одномерными объектами. Замыкая такой
- 60. Для построения вектора обратной связи
- 61. Управление, при котором корни (моды)
- 62. Модальное управление не позволяет
- 63. Замечание 2 Ограниченность модального управления
- 64. Модальное управление многомерными объектами. Если
- 65. Управление и наблюдение в многомерных системах. Разделяющиеся
- 66. Необходимо разделить объект на подсистемы.
- 67. 2) К выбранным r строкам
- 68. 3) Из выбранных n строк
- 69. 5) Построение оставшихся
- 70. Согласно полученной структуре разделяющихся матриц,
- 71. 1) В качестве первых m
- 72. В результате преобразования
- 73. При линейной зависимости столбцов матрицы В
- 74. 3) Аналогично для b3,b4,…, тогда
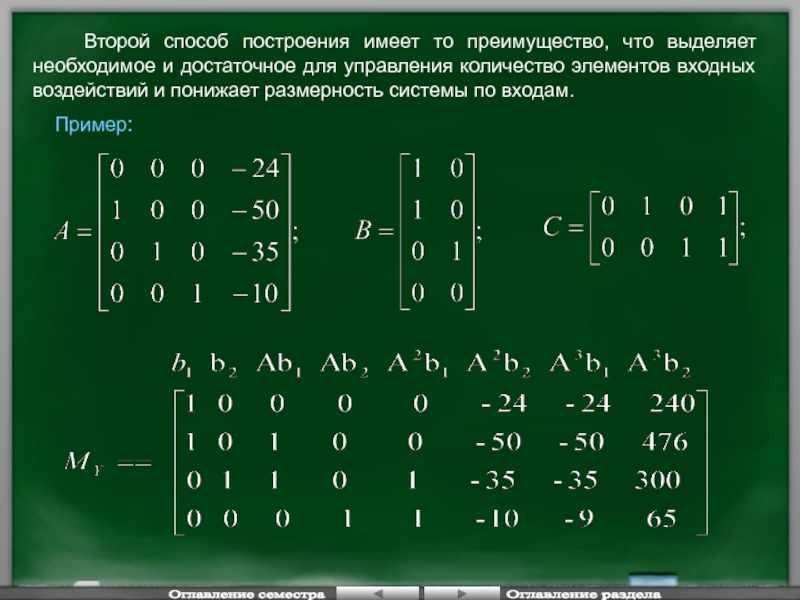
- 75. Второй способ построения имеет то
- 76. При
- 77. Примеры построения многовходовых объектов с использованием разделяющих
- 78. На компьютере можно подобрать оптимальное
- 79. Для правильного построения модального управления
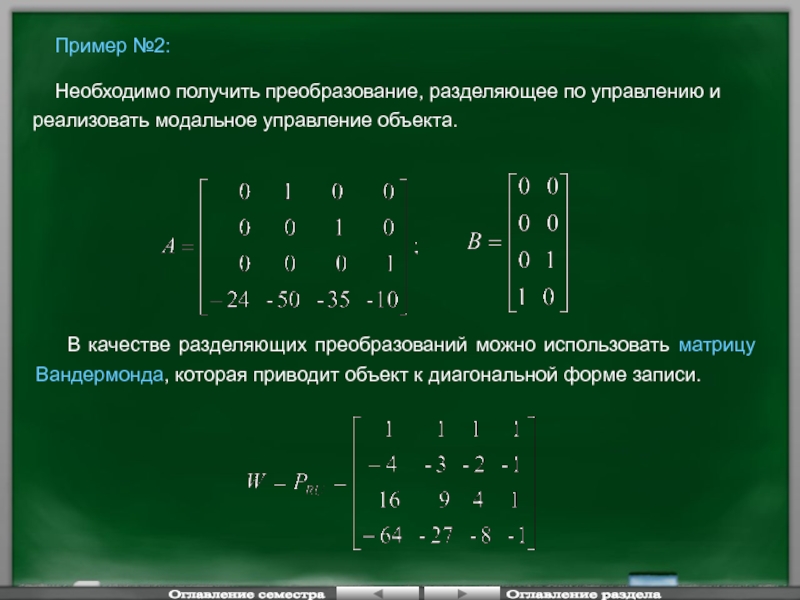
- 80. Пример №2:
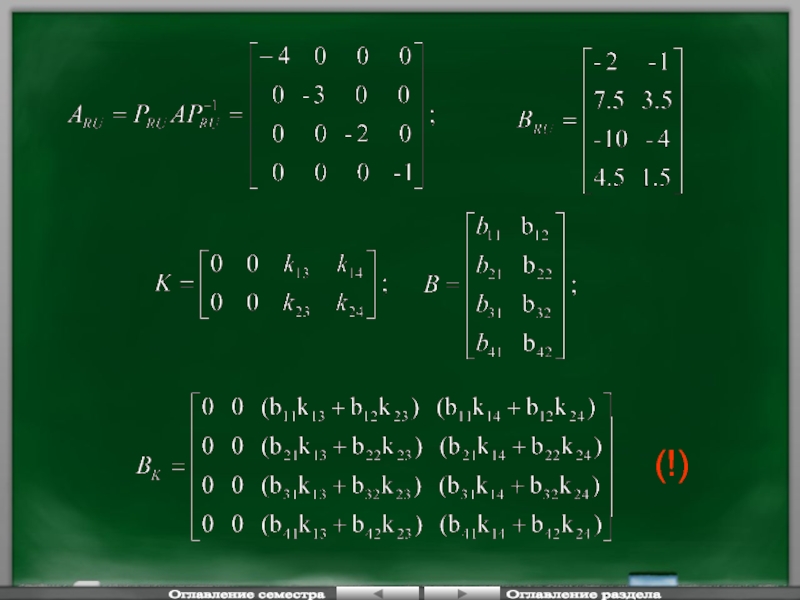
- 81. (!) Оглавление семестра Оглавление раздела
- 82. Оглавление семестра Оглавление раздела
- 83. Оглавление семестра Оглавление раздела
- 84. Если объект не возмущен, то x(t)=0
- 85. Оглавление семестра Оглавление раздела
- 86. Оглавление семестра Оглавление раздела
- 88. (2) (1)
- 89. Свойства фундаментальной матрицы: 1)
- 90. Поэтому переходную матрицу можно определить
- 91. при t = t0 (3)
- 92. По аналогии с экспонентной (3)
- 93. Таким образом можно записать еще
- 94. Вынужденные движения в линейных динамических системах. Теорема:
- 95. (6) Оглавление семестра
- 96. Наиболее часто решение для переходной
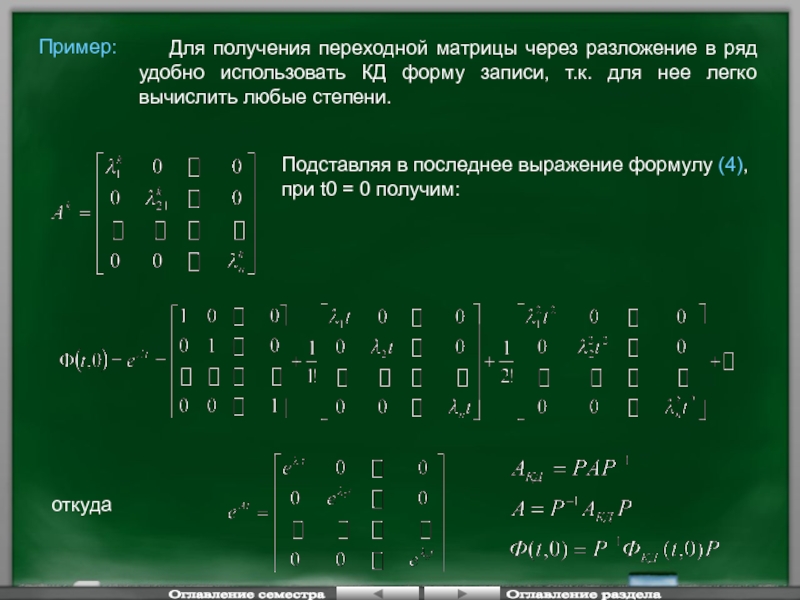
- 97. Для получения переходной матрицы через
- 98. Для применения данного подхода необходимо,
- 99. Пример 2: Необходимо вычислить переходную
- 100. Оценка устойчивости состояния автоматических систем по
- 101. Для общего понятия определения устойчивости
- 102. (*) Оглавление семестра Оглавление
- 103. Оглавление семестра Оглавление раздела
- 104. Одна и та же система
- 105. Служит мерой возмущенного движения
- 106. , такое, что из неравенства Оценка
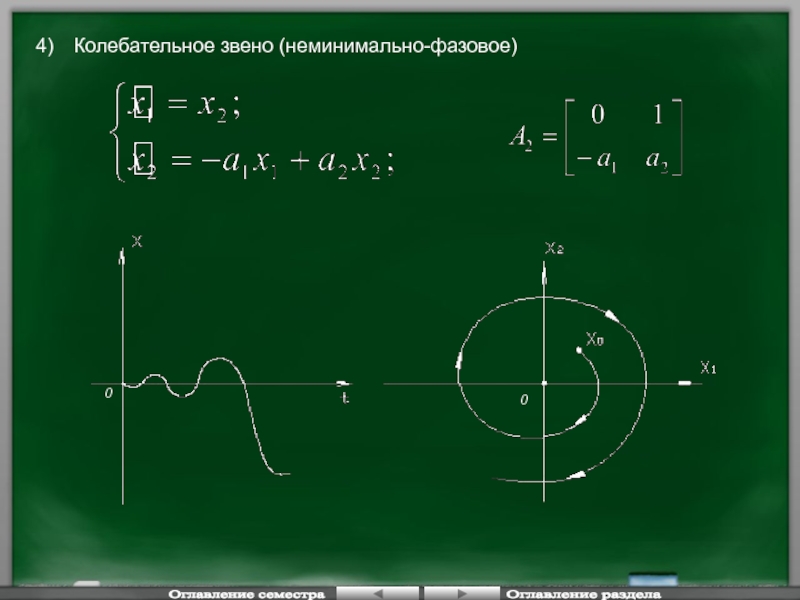
- 108. Консервативное звено
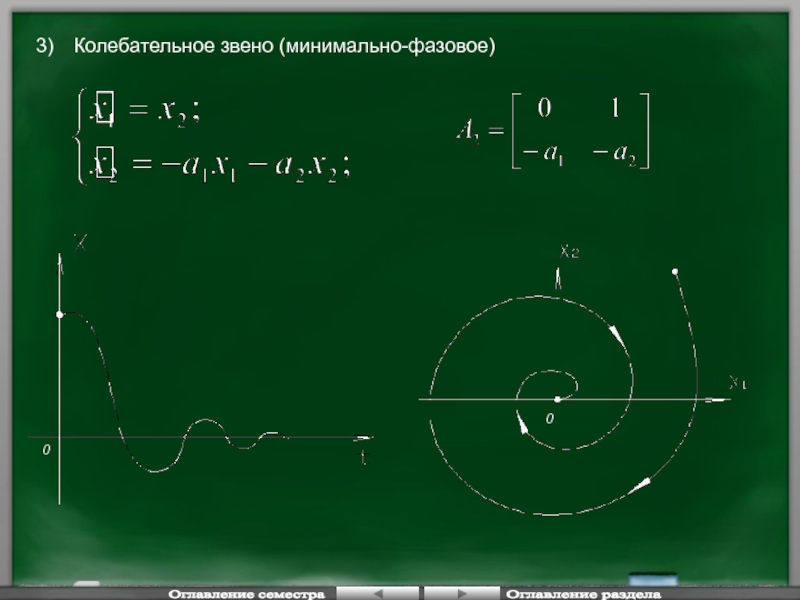
- 109. Колебательное звено (минимально-фазовое) Оглавление семестра Оглавление раздела 0 0 3)
- 110. Оглавление семестра Оглавление раздела 0 0 Колебательное звено (неминимально-фазовое) 4)
- 111. Оценка устойчивости по переходной матрице.
- 112. Оценка устойчивости по спектру линейной системной матрицы.
- 113. Оценка устойчивости замкнутых систем с использованием
- 114. Если в области (*)
- 115. Исследования устойчивости с помощью функции
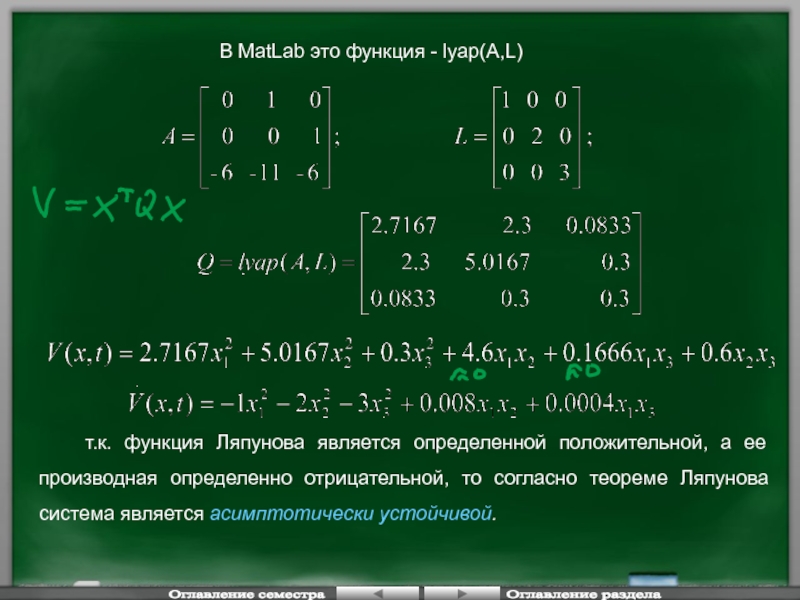
- 116. Т.к. функция
- 117. Теорема Ляпунова для линейных систем.
- 118. В MatLab это функция - lyap(A,L)
- 119. Оценка качества переходных процессов с использованием
- 120. Из выражения (*.1) следует верхняя оценка времени
- 121. 2) Функция Ляпунова заключает в себе значительную
- 122. Для обеспечения отрицательной определенности
- 123. Математическое описание и
- 124. Таким образом промышленная цифровая система
- 125. Иногда смешанное квантование приводит
- 126. Любой из параметров
- 128. Получение матрично-векторных математических моделей ДНСУ
- 129. Последнее выражение по математической
- 130. Заменить
- 131. Пример:
- 133. По диагонали такой матрицы
- 134. Преобразуем системную
- 135. Вычисление переходной матрицы
- 137. 2) Основная
- 138. Оглавление семестра Оглавление раздела
- 139. Оценка фундаментальных свойств ДНСУ ДНСУ
- 140. Математические модели процессов в ДНСУ
- 141. При анализе дискретных систем с
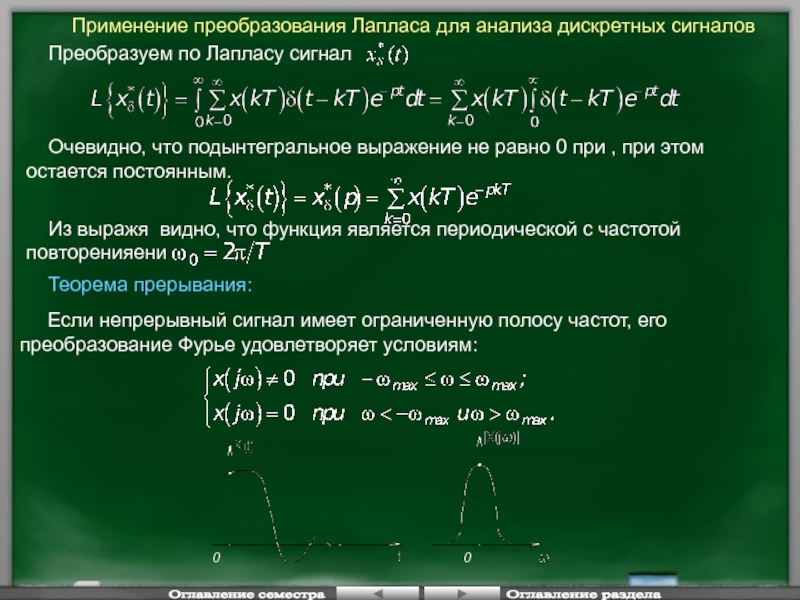
- 142. Применение преобразования Лапласа для анализа дискретных
- 143. Если же частота квантования не
- 144. Анализ качества дискретных систем:
- 145. Оглавление семестра Оглавление раздела 0 0
- 146. Выделение области с заданной степенью устойчивости:
- 147. Выделение области равной степени затухания (или колебательности):
Слайд 2Учебный курс
«Теория Автоматического Управления»
Современная ТАУ
Описание одномерных и многомерных объектов
Связь матрично-векторной и вход-выходной моделей объектов и систем
Понятия управляемости и наблюдаемости
Понятие базиса в пространстве состояний
Основные формы представления математических моделей
Наблюдатели состояний
Далее ?
Слайд 3Современная ТАУ
Системы с обратной связью по состоянию
Управление и наблюдение
Закономерности движения
Оценка устойчивости состояния автоматических систем
Оценка устойчивости замкнутых систем с использованием функции Ляпунова
Математическое описание и исследование дискретно-непрерывных систем управления.
Слайд 4Описание одномерных и многомерных объектов и систем
в пространстве состояний
Основные
Оглавление семестра
Математическое описание в пространстве состояний
Слайд 5Связь матрично-векторной и вход-выходной моделей объектов и систем
Построение МВ ММ
Оглавление семестра
Построение МВ ММ по структурной схеме
Построение вход-выходных моделей по матрично-векторным
Техника вычисления передаточных матриц
Слайд 6Понятия управляемости и наблюдаемости
Понятие управляемости
Оглавление семестра
Понятие наблюдаемости и
Понятие стабилизируемости, детектируемости и идентифицируемости
Слайд 7Понятия базиса в пространстве состояний
Основные понятия и определения
Оглавление семестра
Слайд 8Наблюдатели состояний
Основные понятия и определения
Оглавление семестра
Редуцированный наблюдатель
Слайд 9Системы с обратной связью по состояниям
Основные понятия и определения
Оглавление семестра
Модальное управление одномерными объектами
Модальное управление многомерными объектами
Слайд 10Управление и наблюдение в многомерных системах. Разделяющее преобразование.
Многомерный ДНС Луенбергера.
Оглавление семестра
Преобразование, разделяющееся по наблюдению
Преобразование, разделяющееся по управлению
Возможности систем обратных связей для многовходовых объектов. Примеры построения многовходовых объектов
Слайд 11Закономерности движения
Понятия возмущенного и невозмущенного движений
Оглавление семестра
Свободное движение
Слайд 12Оценка устойчивости состояния автоматических систем
Понятие устойчивости в пространстве состояний
Оглавление семестра
Оценка устойчивости по Ляпунову
Оценка устойчивости по переходной матрице
Оценка устойчивости по спектру линейной системной матрицы
Слайд 13Оценка устойчивости замкнутых систем с использованием функции Ляпунова
Основные понятия и
Оглавление семестра
Построение функции Ляпунова на основе матрично-векторной модели.
Теорема Ляпунова для линейных систем
Оценка качества переходных процессов
Слайд 14Математическое описание и исследование дискретно-непрерывных систем управления
Основные понятия и определения
Вычисление переходной матрицы состояния ДНСУ
Эквивалентные преобразования матрично-векторных моделей линейных ДНСУ
Оценка фундаментальных свойств ДНСУ
Математические модели процессов в ДНСУ
Оглавление семестра
Слайд 15Основные понятия и определения.
Описание одномерных и многомерных объектов
и систем в
Переменные состояния – это некоторые внутренние переменные объекта или системы, характеризующие ее динамические свойства.
Описание в пространстве состояний – это представление математической модели объекта или системы с использованием переменных состояния.
Оглавление семестра
Оглавление раздела
Слайд 16уравнение состояний
уравнение наблюдений
Матрично-векторная математическая модель (МВММ) строится на основе
- матрицы
- вектора
- системная матрица (характеризует фундаментальные
свойства объекта или системы, n – размерность объекта)
- матрица управлений (m – количество управляющих входов)
- матрица возмущений (r – количество возмущающих входов)
матрица выходов (показывает взаимосвязь между
переменными состояния и выходами, p – количество выходов)
матрица взаимосвязей управлений с выходами
матрица взаимосвязей возмущений с выходами
Математическое описание в пространстве состояний
Оглавление семестра
Оглавление раздела
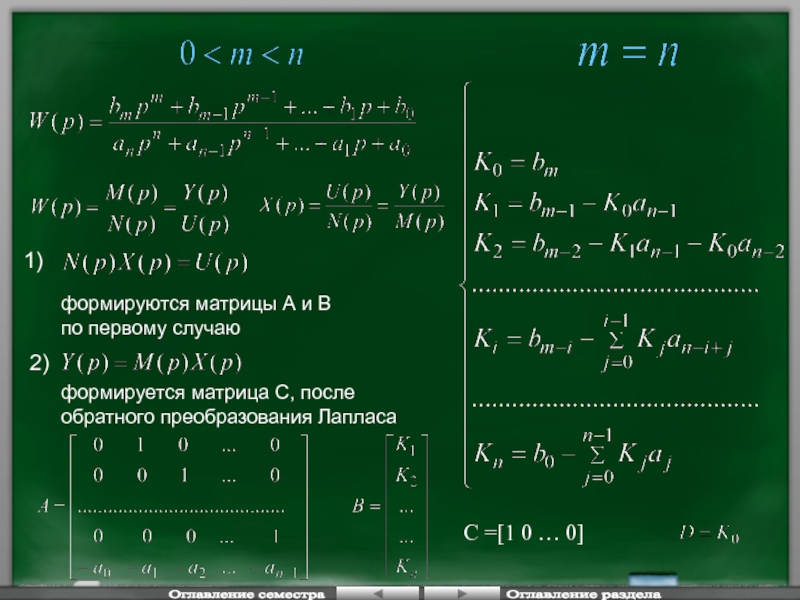
Слайд 17 В зависимости от соотношения степеней полиномов числителя и
знаменателя
После применения обратного преобразования Лапласа
Связь матрично-векторной и вход-выходной моделей объектов и систем
Построение МВ ММ по вход-выходной модели
Оглавление семестра
Оглавление раздела
Слайд 19Пример
Дан объект управления
С=[1 0 0]
Необходимо построить МВ ММ
Оглавление семестра
Оглавление
Слайд 20
1)
2)
формируются матрицы А и В
по первому случаю
формируется
обратного преобразования Лапласа
C =[1 0 … 0]
Оглавление семестра
Оглавление раздела
Слайд 21Алгоритм построения:
Исходная математическая модель, представленная в графической
форме преобразуется к структуре,
звенья нулевого или первого порядков (ПЗ или ИЗ).
На выходах динамических звеньев первого порядка назначаются
переменные состояния
выходы звеньев нулевого порядка
не обозначаются (они входят в МВ ММ в качестве коэффициентов).
Формируются сигналы на входах динамических звеньев, согласно
полученной на первых этапах структуре, при этом участвуют
как назначенные переменные состояния, так и сумматоры и звенья
нулевого порядка.
Составляется система операторных алгебраических уравнений, после
применения обратного преобразования Лапласа она преобразуется
в систему дифференциальных уравнений в форме Коши, по которой
строится МВ ММ.
Построение МВ ММ по структурной схеме.
1)
2)
3)
4)
Оглавление семестра
Оглавление раздела
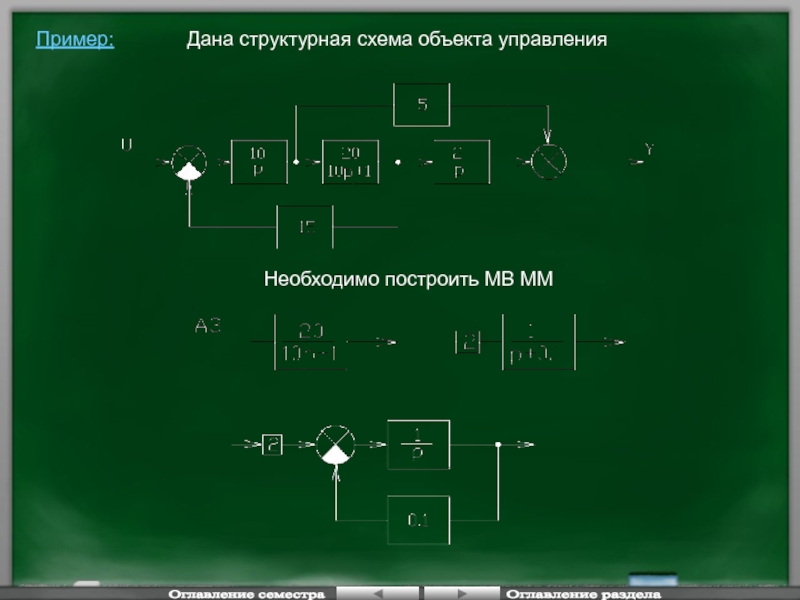
Слайд 22Пример:
Дана структурная схема объекта управления
Необходимо построить МВ ММ
Оглавление семестра
Оглавление раздела
Слайд 24
характеристическая матрица
характеристический полином
→
Передаточные матрицы (ПМ) по состоянию
Построение вход-выходных
Оглавление семестра
Оглавление раздела
Слайд 25
Передаточная матрица – это матрица, в ячейках которой стоят
передаточные функции по
Передаточные матрицы по выходам
Пример
Оглавление семестра
Оглавление раздела
Слайд 26 Основной задачей при построении передаточных матриц является
нахождение
В случае высокой размерности объекта это может представлять особые
трудности, поэтому для построения передаточной матрицы использую
специальные алгоритмы.
Самым распространенным является алгоритм Леверье-Фадеева.
- след матрицы
проверочный шаг
Техника вычисления передаточных матриц
Оглавление семестра
Оглавление раздела
Слайд 27
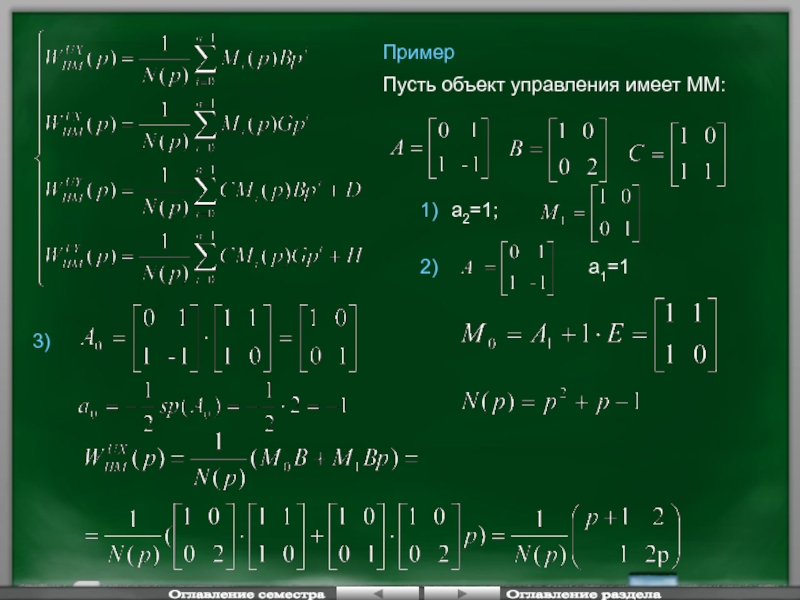
Пример
1)
2)
а1=1
3)
Пусть объект управления имеет ММ:
a2=1;
Оглавление семестра
Оглавление раздела
Слайд 28
Оглавление семестра
Оглавление раздела
Заключение: Полученные результаты показывают, что переход от
Слайд 291. Можно ли, выбрав соответствующим образом входы U(t) перевести ОУ из
Понятия управляемости и наблюдаемости динамических систем.
Оглавление семестра
Оглавление раздела
Пренебрежением фактором управления или наблюдения объекта может привести к ошибочным результатам, в связи с этим рассматривается два важных понятия:
- наблюдаемость ;
- управляемость.
В результате возникают два важных вопроса:
2. Можно ли, наблюдая вектор выходов Y(t) в течение достаточно длительного промежутка времени определить начальное состояние объекта?
Слайд 30Оглавление семестра
Оглавление раздела
Объект называется полностью управляемым, если для любых
Для оценки управляемости используем теорему Калмана:
Для полной управляемости объекта необходимо и достаточно, чтобы матрица управляемости
имела ранг размерности объекта n. Если ранг меньше n, но больше 0, значит объект частично управляемый, если ранг равен 0, то неуправляемый.
Понятие управляемости.
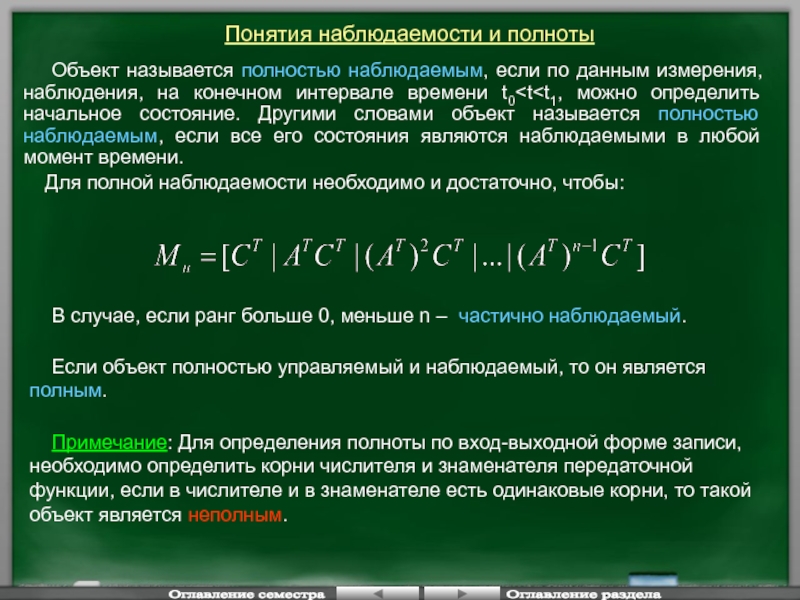
Слайд 31 Объект называется полностью наблюдаемым, если по данным измерения, наблюдения,
Понятия наблюдаемости и полноты
В случае, если ранг больше 0, меньше n – частично наблюдаемый.
Оглавление семестра
Оглавление раздела
Если объект полностью управляемый и наблюдаемый, то он является полным.
Примечание: Для определения полноты по вход-выходной форме записи, необходимо определить корни числителя и знаменателя передаточной функции, если в числителе и в знаменателе есть одинаковые корни, то такой объект является неполным.
Слайд 32 Частично управляемый объект является стабилизируемым в том случае, если
Понятие стабилизируемости, детектируемости и идентифицируемости
Объект называется детектируемым, если системная матрица его не наблюдаемой части имеет устойчивый спектр корней.
Объект называется идентифицируемым, если по измерениям переменных состояния на некотором интервале можно найти матрицу A.
Оглавление семестра
Оглавление раздела
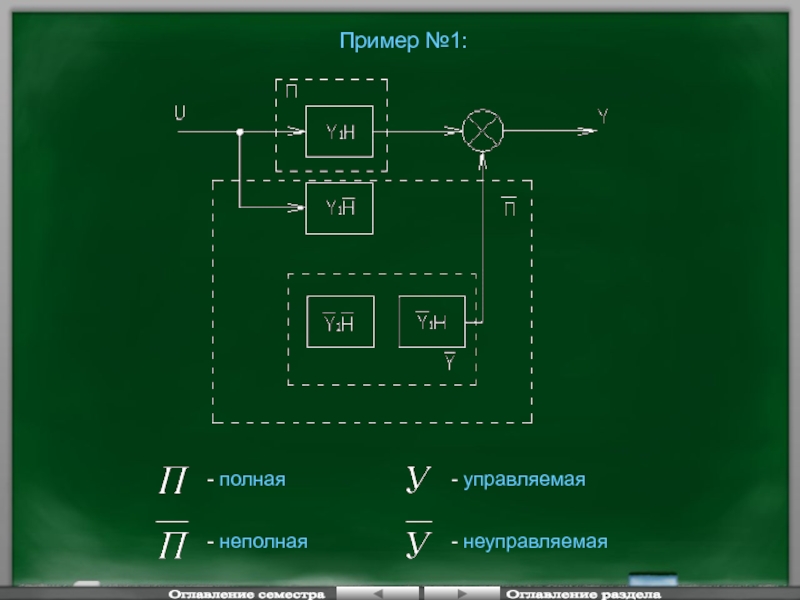
Слайд 33Пример №1:
- полная
- неполная
- управляемая
- неуправляемая
Оглавление семестра
Оглавление раздела
Слайд 34Пример №2:
Определим управляемость и наблюдаемость:
Объект является частично управляемым, т.к.
Оглавление семестра
Оглавление раздела
Слайд 35 Система всегда записана относительно некоторых конкретных базовых векторов ,
Форма записи матрично-векторных моделей не является единственной для каждых конкретных A,B,C, конкретные A,B,C соответствуют некоторому конкретному базису в пространстве состояний. Любое n-мерное линейное пространство имеет множество различных базисов.
Для перехода к новому базису существует некоторое преобразование, которое обозначается: .
Это преобразование должно удовлетворять следующим условиям: - p – квадратная матрица и невырожденная [ ].
Понятие базиса в пространстве состояний
Оглавление семестра
Оглавление раздела
Слайд 36 Поиск необходимого преобразования P может быть различным в зависимости
2) Преобразование на основе свойств наблюдаемости
Для его построения необходимо, чтобы объект был полностью наблюдаемым.
(1)
(2)
Общие закономерности преобразования МВ ММ к произвольно выбранному базису
Необходимо, чтобы объект был полностью управляемым. После определения преобразования
обязательно необходимо сделать его проверку.
1) Преобразование на основе управляемости
Если преобразование из исходного базиса в новый не дает положительного результата, то преобразовать объект исходного базиса в заданный невозможно.
Оглавление семестра
Оглавление раздела
Слайд 37 Для исследования динамических систем в пространстве состояний в теории
1) Основная нормальная форма (ОН)
В ОН форме управляемой матрица В имеет стандартную форму, а С может быть произвольной.
В ОН форме наблюдаемой матрица С должна быть стандартной, а В может быть произвольной.
Для перехода к ОН форме используют преобразования (1) и (2).
Основные формы представления МВ ММ и способы перехода к ним
Оглавление семестра
Слайд 382) Транспонированная ОН (ТОН)
Для перехода к данной форме, обычно
а)
Исходный базис должен быть в ОН – форме.
, где - матрица управляемости
б)
Оглавление семестра
Слайд 39Для перехода к ней применяют преобразования (1) или (2).
5) Каноническая диагональная
где - собственные числа матрицы А
4) Обратная нормальная форма
3) Дополнительная нормальная форма
Оглавление семестра
Слайд 40 Для перехода к данной форме записи используют специальные преобразования
Для перехода к диагональной форме записи необходимо сначала преобразовать к ОН форме.
6) Жорданово - каноническая форма
,где - клетки Жордана
7) Треугольная форма
Из данных 7 форм, наибольшее распространение получили три:
а) ОН
б) ТОН
в) КД
Оглавление семестра
Слайд 41 Динамический наблюдатель состояния (ДНС) – техническое устройство, позволяющее с
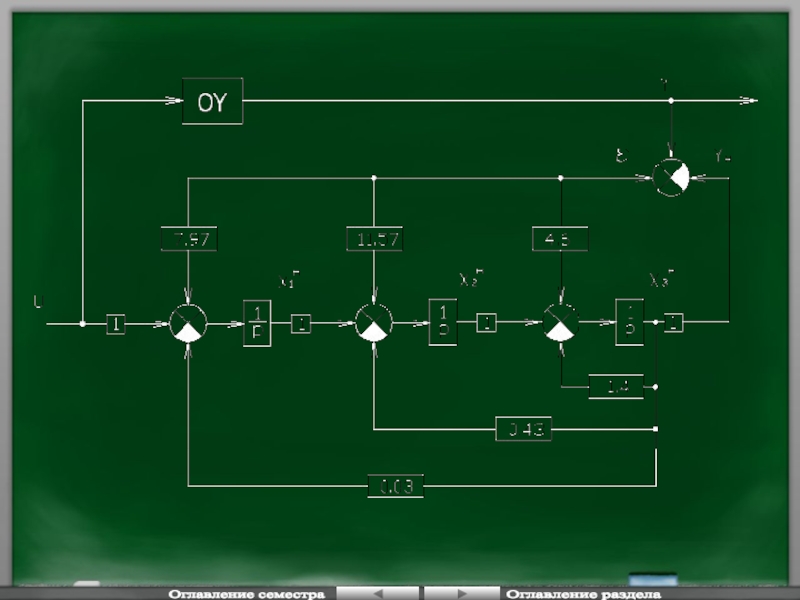
Схема наблюдателя:
Наблюдатели (идентификаторы) состояния линейных динамических объектов и систем
Оглавление семестра
Оглавление раздела
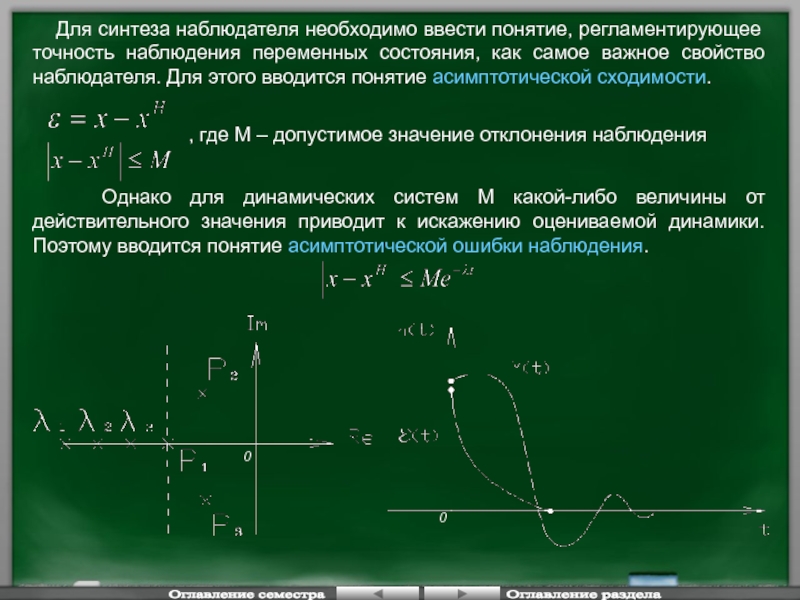
Слайд 42 Для синтеза наблюдателя необходимо ввести понятие, регламентирующее точность наблюдения
, где М – допустимое значение отклонения наблюдения
Однако для динамических систем М какой-либо величины от действительного значения приводит к искажению оцениваемой динамики. Поэтому вводится понятие асимптотической ошибки наблюдения.
Оглавление семестра
Оглавление раздела
0
0
Слайд 43 В теории управления применяется 2 типа наблюдателей состояний:
1)
2) Наблюдатель состояния Луенбергера (так называемый редуцированный наблюдатель).
Наиболее распространенным в инженерной практике является ДНС Калмана.
Условия асимптотической оценки наблюдателя состояния:
( - вектор обратных связей наблюдателя, формирующий его динамические свойства).
Модель наблюдателя (Калмана):
Оглавление семестра
Оглавление раздела
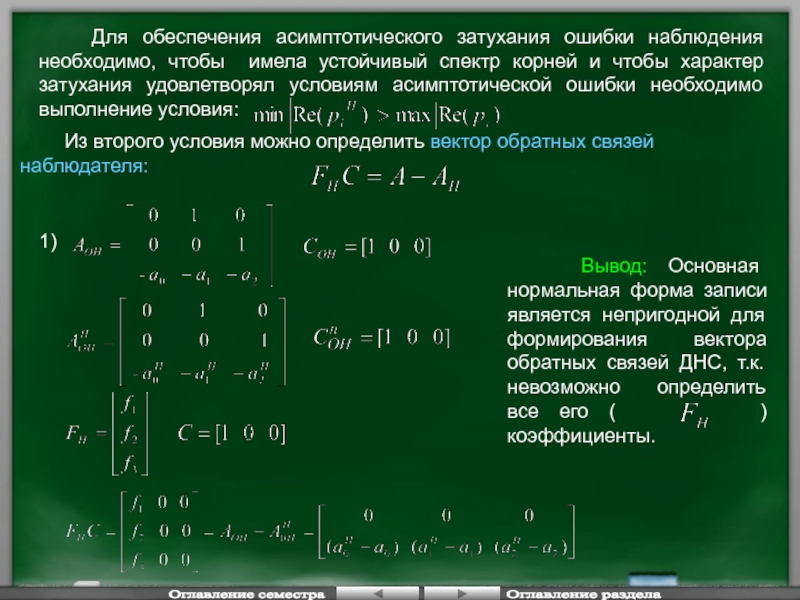
Слайд 44 Для обеспечения асимптотического затухания ошибки наблюдения необходимо, чтобы имела
Из второго условия можно определить вектор обратных связей наблюдателя:
1)
Вывод: Основная нормальная форма записи является непригодной для формирования вектора обратных связей ДНС, т.к. невозможно определить все его ( ) коэффициенты.
Оглавление семестра
Оглавление раздела
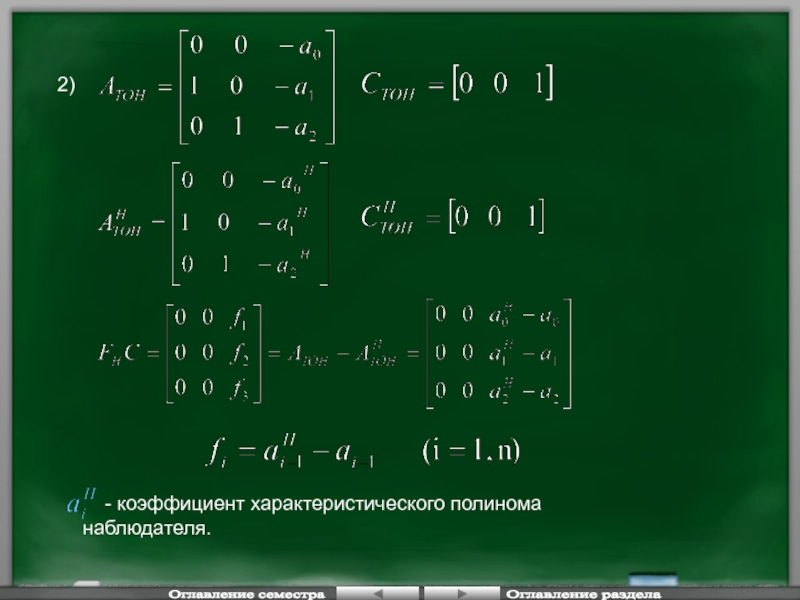
Слайд 452)
- коэффициент характеристического полинома наблюдателя.
Оглавление семестра
Оглавление раздела
Слайд 49 Преимуществом использования ДНС при построении САУ по сравнению с
Достоинство асимптотического ДНС Калмана состоит в его универсальности и в высокой эффективности наблюдаемых переменных состояния, т.е. независимо от причин отклонения действительных значений этих переменных, наблюдаемые переменные сводятся к ним со скоростью, определяемой выбранными значениями собственных чисел наблюдателя.
Оглавление семестра
Оглавление раздела
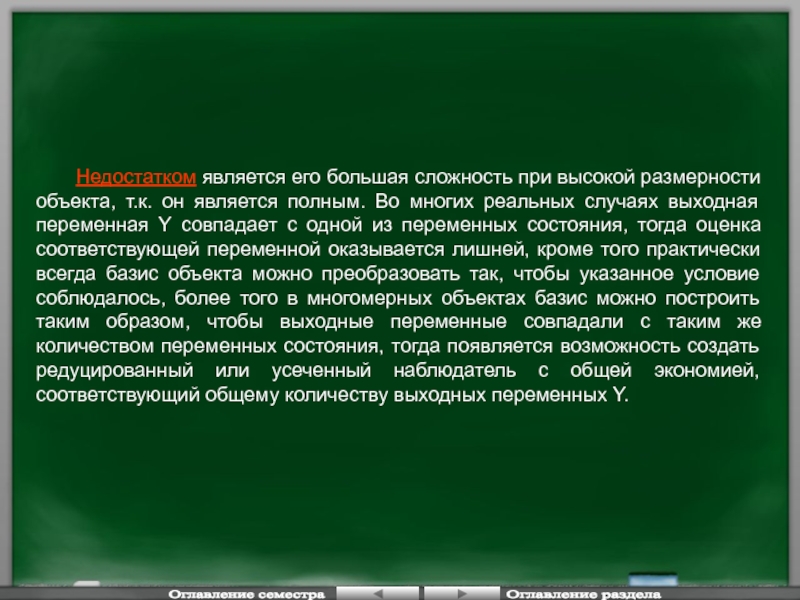
Слайд 50 Недостатком является его большая сложность при высокой размерности объекта, т.к. он
Оглавление семестра
Оглавление раздела
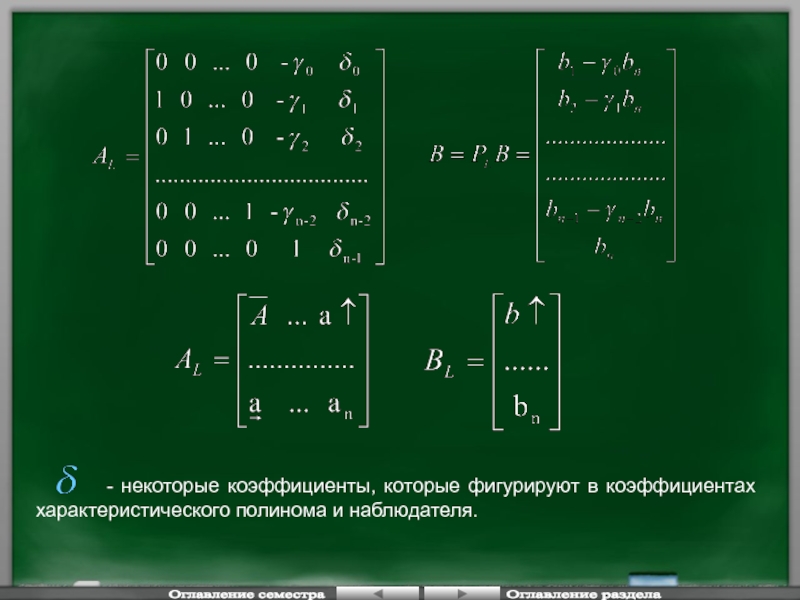
Слайд 51Редуцированный наблюдатель состояния.
Для синтеза ДНС необходимо объект преобразовать к
Необходимо применить преобразование:
- коэффициент характеристического полинома наблюдателя состояний.
Свойства ДНС выбираются аналогично ДНС Калмана, но размерность наблюдателя на единицу меньше размерности объекта.
Оглавление семестра
Оглавление раздела
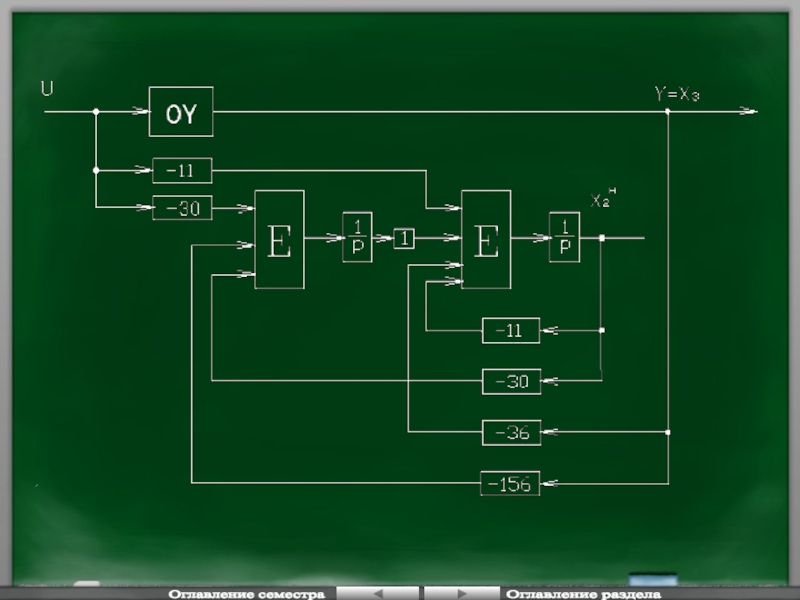
Слайд 52
Оглавление семестра
Оглавление раздела
- некоторые
Слайд 53
Оглавление семестра
Оглавление раздела
После преобразования матрица
имеет ТОН форму
коэффициент γ определяет ее свойства, задавая их с учетом точности наблюдения можно сформировать ДНС.
- уравнение редуцированного наблюдателя Луенберга.
определяет точность работы наблюдателя, т.е. скорость схождения ошибки к нулю, определяется собственными числами матрицы (коэффициент γ), который выбирается по аналогии с ДНС Калмана.
Слайд 57 Недостатком наблюдателя Луенбергера по сравнению с наблюдателем Калмана является
Осуществляется в плане участия переменной в формировании динамики переменной состояния в соответствии с исходной моделью. В результате, выигрывая в простоте реализации наблюдателя проигрывают в точности оценки состояния.
При спонтанных отклонениях начальных значений переменная ошибка наблюдения подавляется с интенсивностью, заданной коэффициентами γ, но при наличии постоянно действующего неконтролируемого воздействия наблюдаемость осуществляется также с постоянной, не равной нулю ошибкой. В этом отношении наблюдатель Калмана более эффективен, чем наблюдатель Луенбергера.
Оглавление семестра
Оглавление раздела
Слайд 58Системы с обратной связью по состоянию
Модальное управление объектами.
Рассмотрение объектов
Такой подход дает больше возможностей для формирования устойчивой системы и придания ей заданного качества, так как n-мерный статический регулятор обратной связи имеет n-степеней свободы, тогда как П - регулятор при вход-выходном описании имеет только одну степень свободы.
Оглавление семестра
Оглавление раздела
Слайд 59Модальное управление одномерными объектами.
Замыкая такой объект обратными связями по переменным состояния
- корни объекта
Оглавление семестра
Оглавление раздела
- корни системы должны быть лучше, чем корни объекта
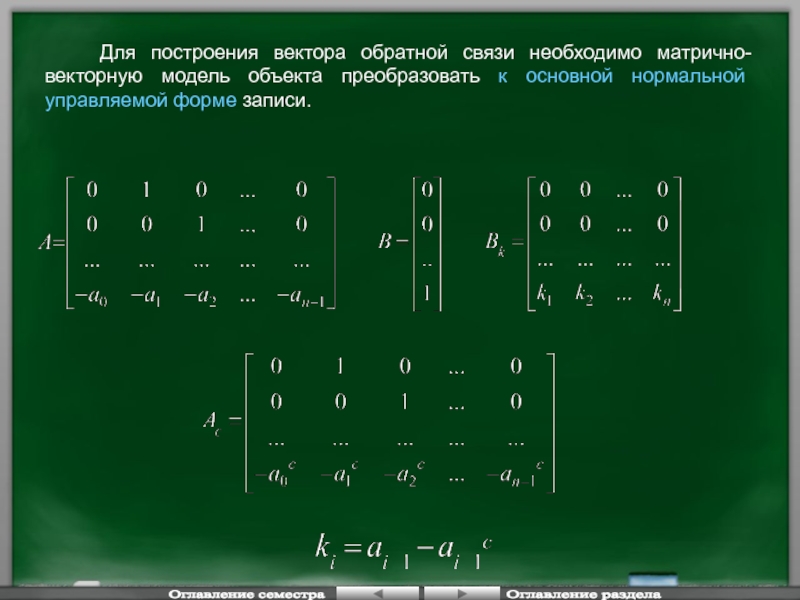
Слайд 60 Для построения вектора обратной связи необходимо матрично-векторную модель объекта
Оглавление семестра
Оглавление раздела
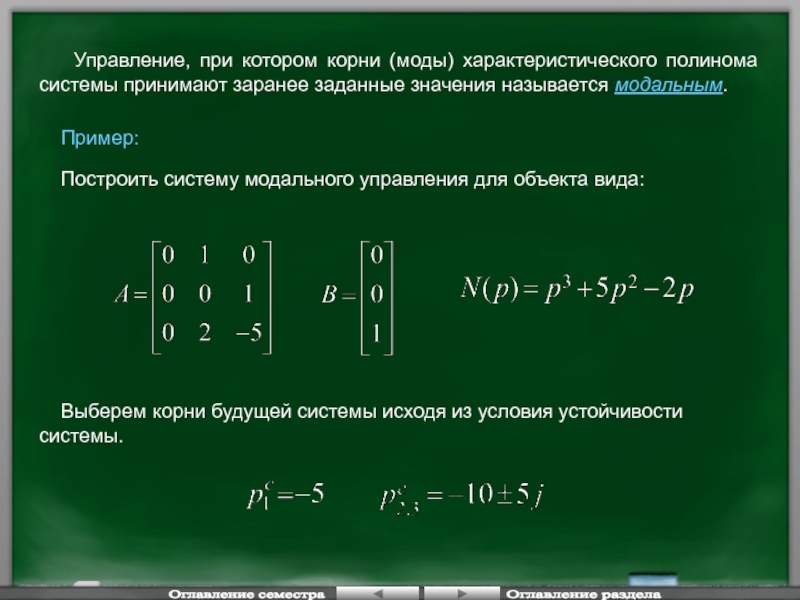
Слайд 61 Управление, при котором корни (моды) характеристического полинома системы принимают
Пример:
Построить систему модального управления для объекта вида:
Выберем корни будущей системы исходя из условия устойчивости системы.
Оглавление семестра
Оглавление раздела
Слайд 62
Модальное управление не позволяет повышать точность работы системы, так
Замечание 1
Оглавление семестра
Оглавление раздела
Слайд 63Замечание 2
Ограниченность модального управления состоит в том, что обратная
Корни системы выбираются лучше, чем у объекта и они должны обеспечивать заданное качество. В данном случае необходимо, чтобы время регулирования было в 5 раз меньше.
Оглавление семестра
Оглавление раздела
Слайд 64Модальное управление многомерными объектами.
Если у объекта количество вводов больше
Оглавление семестра
Оглавление раздела
Слайд 65Управление и наблюдение в многомерных системах.
Разделяющиеся преобразования.
Многомерный ДНС Луенбергера.
Преобразования, разделяющиеся
Для построения такого наблюдателя в многомерном cлучае, необходимо преобразовать ММ объекта таким образом, чтобы она была представлена таким же количеством подсистем, сколько измеряемых выходов имеет объект, тогда возможно построение одномерных НЛ.
Оглавление семестра
Оглавление раздела
(r - количество выходов)
Слайд 66 Необходимо разделить объект на подсистемы.
Алгоритм построения преобразования, разделяющегося по
R – линейно-независимых строк матрицы C
Оглавление семестра
Оглавление раздела
Для обеспечения правильного разделения необходимо, чтобы объект был наблюдаемым (частично).
1) Выбираем в качестве элементов промежуточной матрицы Q, используемой для построения матрицы разделяющейся по наблюдению.
Слайд 67 2) К выбранным r строкам добавляем последовательно, начиная, например,
Оглавление семестра
Оглавление раздела
Слайд 68 3) Из выбранных n строк строим матрицу Q по
4) С использованием обратной матрицы Q, строится матрица преобразования.
Оглавление семестра
Оглавление раздела
Слайд 69
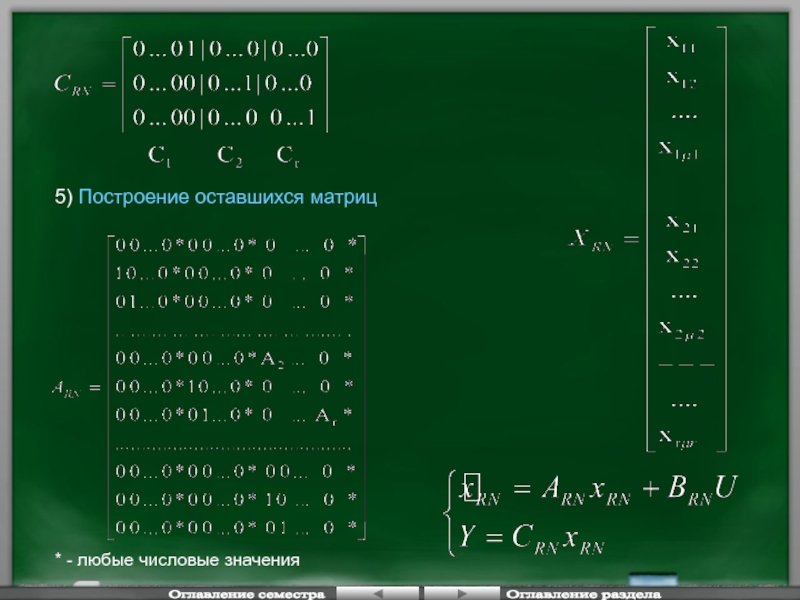
5) Построение оставшихся матриц
* - любые числовые значения
Оглавление семестра
Оглавление раздела
Слайд 70 Согласно полученной структуре разделяющихся матриц, последнею переменную из подсистем
Преобразование, разделяющееся по управлению.
Исходными данными также является система уравнений.
Пусть объект является управляемым и матрица В имеет размерность . Для построения преобразований, разделяющихся по управлению, можно использовать 2 алгоритма:
Оглавление семестра
Оглавление раздела
Слайд 71 1) В качестве первых m столбцов для преобразования
Выбирается m – столбцов матрицы В;
2) К выбранным столбцам последовательно присоединяются столбцы Ab1, Ab2, … и проверяется линейная независимость
каждого последующего от всех предыдущих. Если какой-либо очередной столбец линейно зависим, то дальше наращивание на базе этого столбца не происходит.
Первый алгоритм аналогичен алгоритму по наблюдению:
Оглавление семестра
Оглавление раздела
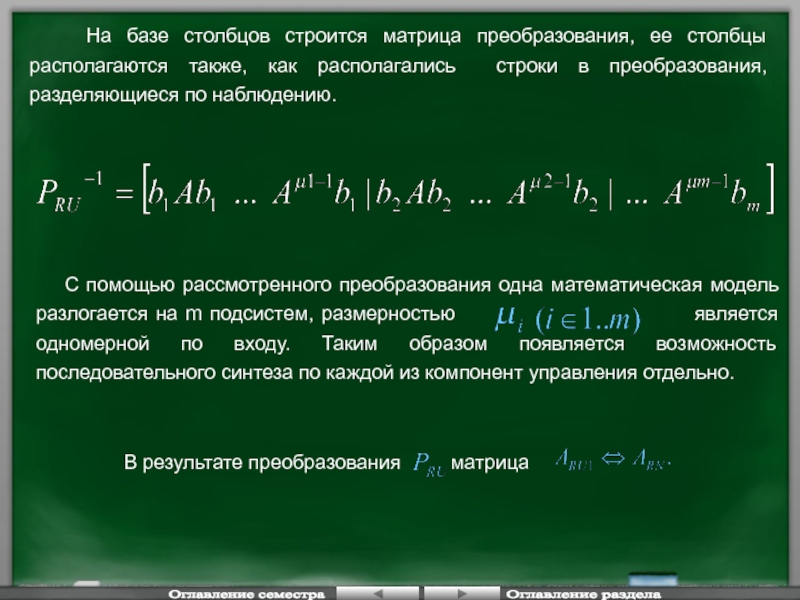
Слайд 72В результате преобразования матрица
С помощью
На базе столбцов строится матрица преобразования, ее столбцы располагаются также, как располагались строки в преобразования, разделяющиеся по наблюдению.
Оглавление семестра
Оглавление раздела
Слайд 73
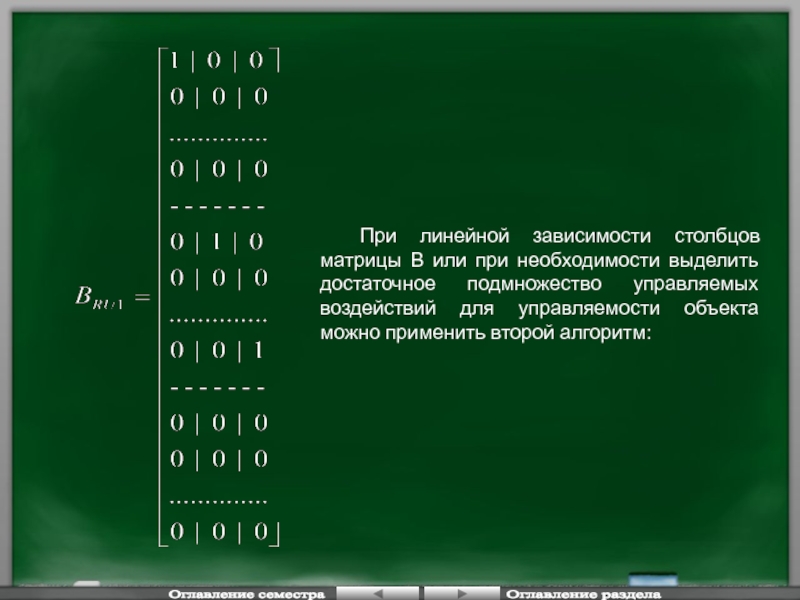
При линейной зависимости столбцов матрицы В или при необходимости выделить достаточное
Оглавление семестра
Оглавление раздела
Слайд 74 3) Аналогично для b3,b4,…, тогда последний член набора показывает,
или до последнего линейно независимого столбца (до n линейно независимых).
1) Строится матрица управляемости (МУ) и из нее выбираются столбцы для преобразования в следующем порядке
последний линейно независимый столбец из набора
2) Если то выбираем из второго столбца
но иметь вид верхней, треугольной клеточной
матрицы, где количество клеток равно q.
Оглавление семестра
Оглавление раздела
Слайд 75 Второй способ построения имеет то преимущество, что выделяет необходимое
Пример:
Оглавление семестра
Оглавление раздела
Слайд 76
При построении системы управления чаще приходится использовать ДНС и
Оглавление семестра
Оглавление раздела
или
Слайд 77Примеры построения многовходовых объектов с использованием разделяющих преобразований.
Возможности систем обратных связей
Пример №1
- необходимо построить модальное управление объектом, разделенным на подсистемы в предыдущем примере.
Оглавление семестра
Оглавление раздела
- матрица
Слайд 78 На компьютере можно подобрать оптимальное значение а0, обеспечивающее второе
Для сохранения структуры матрицы Ас необходимо некоторые элементы матрицы Вк положить нулевыми, а остальные варьировать в зависимости от заданных требований.
Требования к новой системе:
Корень -1 заменить на -5 (p+5)
Остальные корни должны иметь максимум по модулю вещественные части при условии изменения только коэффициента а0
Оглавление семестра
Оглавление раздела
Слайд 79
Для правильного построения модального управления необходимо преобразовать объект и вектор обратных
Оглавление семестра
Оглавление раздела
Слайд 80 Пример №2:
Необходимо получить преобразование, разделяющее по
В качестве разделяющих преобразований можно использовать матрицу Вандермонда, которая приводит объект к диагональной форме записи.
Оглавление семестра
Оглавление раздела
Слайд 84
Если объект не возмущен, то x(t)=0
Закономерности движения линейных систем в
Понятие возмущенных и невозмущенных движений.
Одно или несколько движений устанавливающихся в системе при отсутствии внешних воздействий называются невозмущенными.
Все остальные движения, являющиеся следствием любых воздействий на систему, называются возмущенными.
Оглавление семестра
Оглавление раздела
- это уравнение описывает состояние объекта.
х – состояние
v – вектор входных воздействий
t – время
F – нелинейная функция
- справедлива для стационарных систем
Слайд 85
Оглавление семестра
Оглавление раздела
Для анализа свойств стационарных систем,
Ненулевые начальные условия движения исследования объекта называются возмущениями.
Возмущенные движения системы на некотором интервале времени в отсутствии влияния внешних воздействий называются свободными движениями объекта.
Аналогичное движение при наличии воздействий называется вынужденным.
Слайд 86
Оглавление семестра
Оглавление раздела
В практике теории управления распространенным
Слайд 87 означающее прекращение движения
Положение равновесия исследуемого объекта соответствует равенство нулю всех производных:
где
Оглавление семестра
Оглавление раздела
0
В этом случае переменные состояния принято называть фазовыми координатами, траектории – фазовыми. Часто для наглядности эти траектории отображают на плоскости. Изображение сечения фазовой траектории на плоскости называется портретом.
- нелинейная функция.
Слайд 88
(2)
(1)
Свободные движения в линейной динамической системе.
Для оценки
Динамическая система, описываемая уравнением (1), при условии U(t)=0 называется автономной системой.
Матрица Х(t), [n x n] называется фундаментальной для системы (2)
когда ее столбцы образованы линейно независимыми решениями этой системы
Оглавление семестра
Оглавление раздела
- называется определителем Вронского.
Слайд 89
Свойства фундаментальной матрицы:
1)
2)
3)
4)
Для каждого
Оглавление семестра
Оглавление раздела
1) Должна
2) Должна удовлетворять уравнению
Если матрица X(t) неособенная и удовлетворяет решению данной системы, то она является фундаментальной.
Если Х(t) есть фундаментальная матрица, то называется переходной матрицей.
На основании свойств фундаментальной матрицы дать свойства переходной матрице:
Переходная матрица представляет собой фундаментальную, построенную для единичных начальных условий
Слайд 90 Поэтому переходную матрицу можно определить как решение матричного уравнения:
Определение переходной матрицы и ее свойств относятся к системам,
описываемыми ДУ с постоянными и переменными коэффициентами.
Оглавление семестра
Оглавление раздела
Если х0 - вектор произвольных не нулевых начальных условий,
то решение системы можно найти по следующей формуле:
Слайд 91при t = t0
(3)
Оглавление семестра
Оглавление раздела
В соответствии со свойствами переходной матрицы, это одно из решений матричного ДУ, обращающееся в единичную матрицу каждый раз, когда элементы t и t0 равны руг другу. В случае системы первого порядка переходная матрица вырождается в скалярную функцию.
Следовательно роль переходной матрицы играет решение равное (1).
Слайд 92 По аналогии с экспонентной (3) можно ввести понятия матричного
Если в этой формуле α заменить на матрицу А, то получится некоторая функциональная матрица, которая и называется матричным экспоненциалом:
(4)
Переходной матрицей системы (1) является матричный экспоненциал, определенный равенством (4).
Оглавление семестра
Оглавление раздела
Слайд 93 Таким образом можно записать еще несколько свойств переходной матрицы,
б) если А – скаляр и А=α, то
Оглавление семестра
Оглавление раздела
а) если системная матрица А – постоянная, то
в)
г)
д)
е)
Слайд 94Вынужденные движения в линейных динамических системах.
Теорема:
(5)
Оглавление семестра
Оглавление раздела
то для получения ее решения можно воспользоваться переходной матрицей вида (4), которая позволяет найти это решение методом варьируемых постоянных интегрирования (метод Лагранжа).
Если Φ(t,t0) есть переходная матрица объекта, то единственное решение системы уравнений, при x(t0)=x0 задается формулой
Слайд 95(6)
Оглавление семестра
Оглавление раздела
(6) – формула Коши,
Частным случаем для определения переходной матрицы является вариант, когда t0=0 :
Слайд 96 Наиболее часто решение для переходной матрицы находится с помощью
(7)
Оглавление семестра
Оглавление раздела
Пусть объект описывается неоднородным ДУ.
Применим к уравнению
Преобразование Лапласа при нулевых начальных условиях:
Слайд 97 Для получения переходной матрицы через разложение в ряд удобно
Пример:
откуда
Оглавление семестра
Оглавление раздела
Подставляя в последнее выражение формулу (4), при t0 = 0 получим:
Слайд 98 Для применения данного подхода необходимо, чтобы матрица А не
Пример 1:
Пусть системная матрица объекта имеет вид:
Оглавление семестра
Оглавление раздела
- собственные числа матрицы,
где
Слайд 99Пример 2:
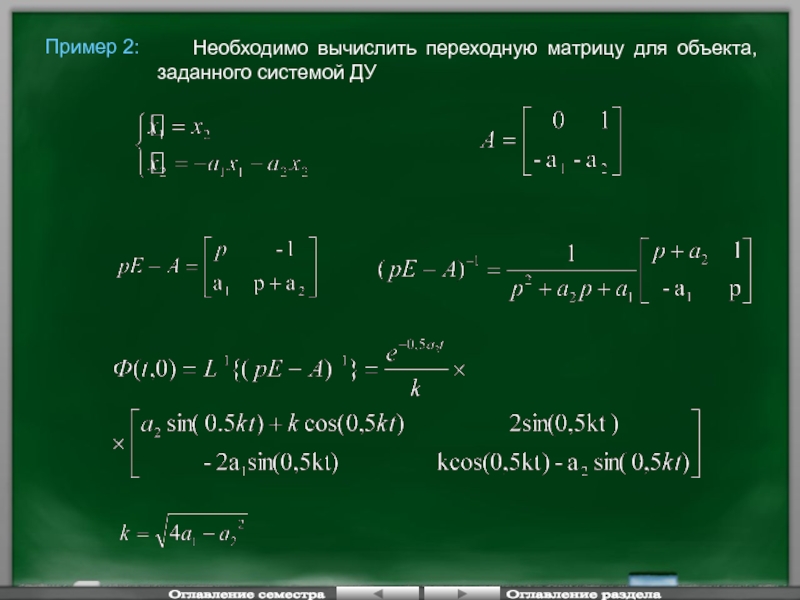
Необходимо вычислить переходную матрицу для объекта, заданного системой
Оглавление семестра
Оглавление раздела
Слайд 100Оценка устойчивости состояния автоматических систем
по матрично-векторной модели.
Понятие устойчивости в пространстве
Оценка устойчивости объектов и систем по вход-выходным критериям является производной от более общей и фундаментальной оценки устойчивости для систем в пространстве состояний. Для произвольных систем (линейных, нелинейных, в полных и частных производных, стационарных и нестационарных) является очень сложной задачей, иногда не решаемой.
Понятие устойчивости является относительным, по своей природе любой объект является физически устойчивым (техническая устойчивость).
В то же время по управляемой входной переменной он может быть неустойчивым, при этом при рассмотрении объектов и измерений может рассматриваться как устойчивый, так и неустойчивый, потому говорят не об устойчивости объекта, а устойчивости движения.
Оглавление семестра
Оглавление раздела
Слайд 101 Для общего понятия определения устойчивости назначим 2 множества:
Оглавление семестра
Оглавление раздела
Для определения большинства понятий устойчивости обычно используют конечномерное евклидово пространство состояния
1) Множество начальных состояний
2) Множество конечных состояний
Gk в общем случае также задается в Rn и времени t. Его элементы обычно удовлетворяют уравнению движения объекта и системы.
Область G0 обычно имеет ту же размерность, что и пространство состояний (n), область Gk (
Слайд 102(*)
Оглавление семестра
Оглавление раздела
0
0
Если уравнение (*) x
а) внутри G0 находится Gk
б) Gk вне этой области
(распространен в технических системах).
Слайд 103Оглавление семестра
Оглавление раздела
0
0
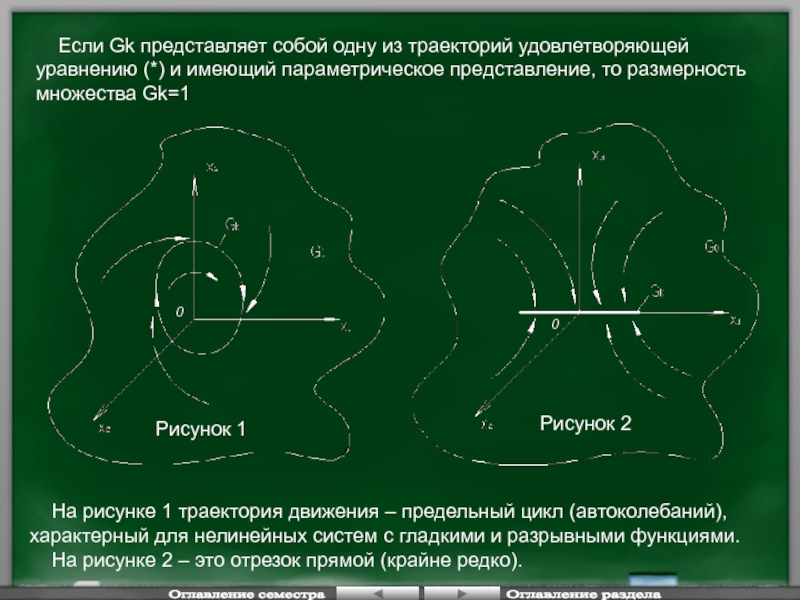
Если Gk представляет собой одну
На рисунке 1 траектория движения – предельный цикл (автоколебаний), характерный для нелинейных систем с гладкими и разрывными функциями.
На рисунке 2 – это отрезок прямой (крайне редко).
Рисунок 1
Рисунок 2
Слайд 104 Одна и та же система может иметь несколько множеств
Оглавление семестра
Оглавление раздела
0
В качестве множества Gk может выступать поверхность (цилиндр), любой размерности, на котором лежат траектории, которые соответствуют уравнению (*).
Множество Gk будем называть множеством невозмущенных состояния или движений, а множество G0 - областью притяжения при наличии устойчивости.
Множество невозмущенных состояний (движений) называется асимптотически устойчивым с областью притяжения G0, если всякие движения начавшиеся в G0 в силу уравнений или законов движения динамической системы, приходит сколь угодно малую окрестность Gk с течением времени.
Слайд 105
Служит мерой возмущенного движения
Оглавление семестра
Оглавление раздела
- норма вектора состояний x
Слайд 106, такое, что из неравенства
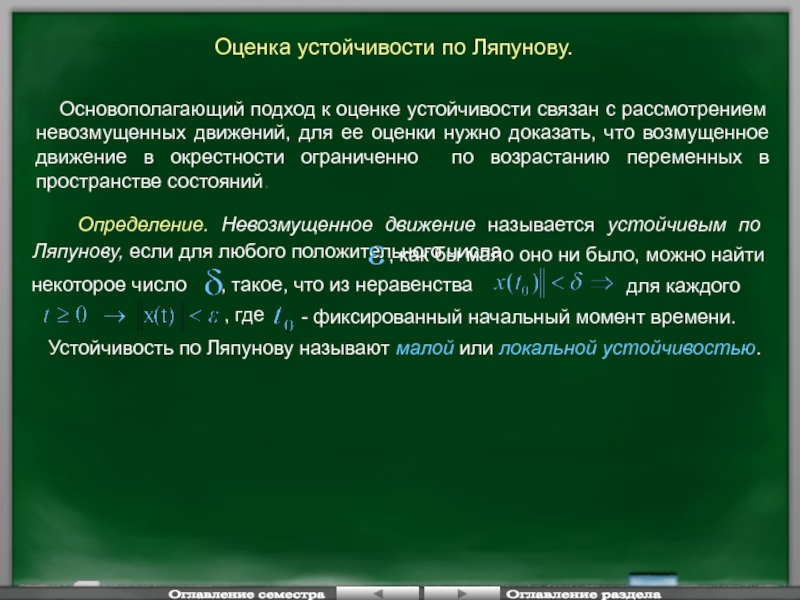
Оценка устойчивости по Ляпунову.
Основополагающий
Определение. Невозмущенное движение называется устойчивым по Ляпунову, если для любого положительного числа
, как бы мало оно ни было, можно найти
для каждого
, где
- фиксированный начальный момент времени.
некоторое число
Устойчивость по Ляпунову называют малой или локальной устойчивостью.
Оглавление семестра
Оглавление раздела
Слайд 107
Здесь подменяется ,
Оглавление семестра
Оглавление раздела
0
0
при
Определение. Движение и соответственно его равновесное положение, устойчивое по Ляпунову и отвечающее дополнительному относительно предыдущего определения свойству
называется асимптотически устойчивым.
Устойчивые линейные системы всегда являются асимптотически устойчивым .
Слайд 108
Консервативное звено (генератор синусоидальных колебаний)
Оглавление семестра
Оглавление раздела
Примеры
1)
2)
Странный аттрактор
0
Слайд 111Оценка устойчивости по переходной матрице.
Для оценки устойчивости достаточно анализировать
При исследовании
возможно три случая:
1) Переходная матрица является ограниченной: для каждого
если переходная матрица ограничена, то можно
показать, что
если
то будет выполняться
условие устойчивости по Ляпунову.
2) Переходная матрица – асимптотически затухающая функция времени
т.е. второй случай соответствует асимптотической устойчивости.
3) Неограниченная матрица, т.е. в ней есть хотя бы один элемент, который
т.е. движение того элемента
является расходящимся – неустойчивое движение.
неограничен на интервале времени
Оглавление семестра
Оглавление раздела
Слайд 112Оценка устойчивости по спектру линейной системной матрицы.
1) Объект является устойчивым по
2) Неустойчивым, если условие следующее:
3) Является асимптотически устойчивым, если
Доказательством этих условий является решение однородных уравнений по формуле Коши:
Оглавление семестра
Оглавление раздела
Слайд 113Оценка устойчивости замкнутых систем
с использованием функции Ляпунова.
Основные понятия и определения.
Функция Ляпунова
- это непрерывная вещественная функция,
определенная в n-мерном пространстве
,имеющая определенный знак,
непрерывные частные производные в области
и равная нулю только в
начале координат. Другими словами,
- шаг радиуса R.
Для оценки устойчивости функции Ляпунова необходимо знать понятия знакоопределенности функции.
Функцию
назовем определенно положительной в области (*),
если всюду в этой области, кроме начала координат, имеет смысл неравенство
Если же выполняется неравенство
то функция
называется определенно отрицательной
(общее название - функция
знакоопределенная).
Оглавление семестра
Оглавление раздела
Слайд 114
Если в области (*) имеет место всюду неравенство
или
то функция
К примеру функция
определенно положительной ,
функция
будет знакопостоянной в пространстве
Функция
является определенно отрицательной в пространстве
Теорема 1: (об устойчивости)
Если для системы
(**)
существует в области R знакопостоянная
функция V(x,t), производная которой по времени, взятая в силу системы (**),
является знакопостоянной функцией знака, противоположного знаку функции
V(x,t), то положение равновесия устойчиво в смысле Ляпунова.
Теорема 2: (об асимптотической устойчивости)
Если для системы (**) существует знакоопределенная функция V(x,t), полная
производная которой по времени, найденная в силу системы (**), будет также
знакоопределенной, знака противоположного с V(x,t), то положение равновесия
будет асимптотически устойчивым.
Оглавление семестра
Оглавление раздела
Слайд 115 Исследования устойчивости с помощью функции Ляпунова получило название второго
В соответствии с представленными теоремами для оценки устойчивости можно построить знакоопределенную функцию и убедившись в отрицательной определенности ее производной доказать неустойчивость.
Построение функции Ляпунова на основе матрично-векторной модели.
Наибольшее распространение получила квадратичная форма функции Ляпунова:
- положительно определенная симметричная матрица
Условие определенной положительности квадратичных форм задается
неравенствами Сильвестра, согласно которых, проверка знакоопределенности
функций Ляпунова делается очень легко.
Считается что
если собственные числа матрицы Q положительны.
Оглавление семестра
Оглавление раздела
Слайд 116
Т.к. функция Ляпунова
в n-мерном пространстве, то она является
функцией n-переменных, которые
по времени от функции квадратичной формы определяется как производная
от сложной функции.
- уравнение Ляпунова (***),
где L – положительно определенная матрица.
Оглавление семестра
Оглавление раздела
Слайд 117Теорема Ляпунова для линейных систем.
Для того, чтобы системная матрица
Таким образом, задавшись любой положительно определенной матрицей L , можно построить функцию Ляпунова (для линейных систем с устойчивой матрицей A (***) существует всегда).
1)
т.е. она является симметричной
2)
наблюдается взаимно-однозначное
При построении функции Ляпунова рекомендуется задавать матрицу L в диагональной форме записи, по диагонали стоят собственные числа, определяется знак матрицы, а выше и ниже диагонали нули, определяющие симметричность матрицы.
Оглавление семестра
Оглавление раздела
Слайд 118В MatLab это функция - lyap(A,L)
т.к. функция Ляпунова является
Оглавление семестра
Оглавление раздела
Слайд 119Оценка качества переходных процессов
с использованием функции Ляпунова.
Оценка времени затухания возмущенного
Функция Ляпунова наряду с основной задачей получения достаточных условий
устойчивости могут использоваться также для оценки отдельных показателей
качества, т.е. качества собственных движений замкнутой системы.
- наименьшее и наибольшее собственные числа матрицы Q.
После дифференцирования, интегрирования и экспонирования получится
неравенство вида:
(*.1)
t – время;
- значение функции Ляпунова для определенных начальных условий.
Оглавление семестра
Оглавление раздела
Слайд 120Из выражения (*.1) следует верхняя оценка времени затухания переходного
процесса, как
- окрестность.
Если в выражении (*.1) вместо х подставить
можно получить оценку
переходного процесса.
(*.2)
Если требуется нижняя оценка времени затухания возмущенного движения,
то используют (*.1).
Выводы по использованию второго метода Ляпунова.
1) Является эффективным методом оценки устойчивости систем управления
без решения их математических моделей, даже в нелинейном случае,
а для линейных систем существуют регулярные алгоритмы построения
функции Ляпунова для системы линейного порядка.
Оглавление семестра
Оглавление раздела
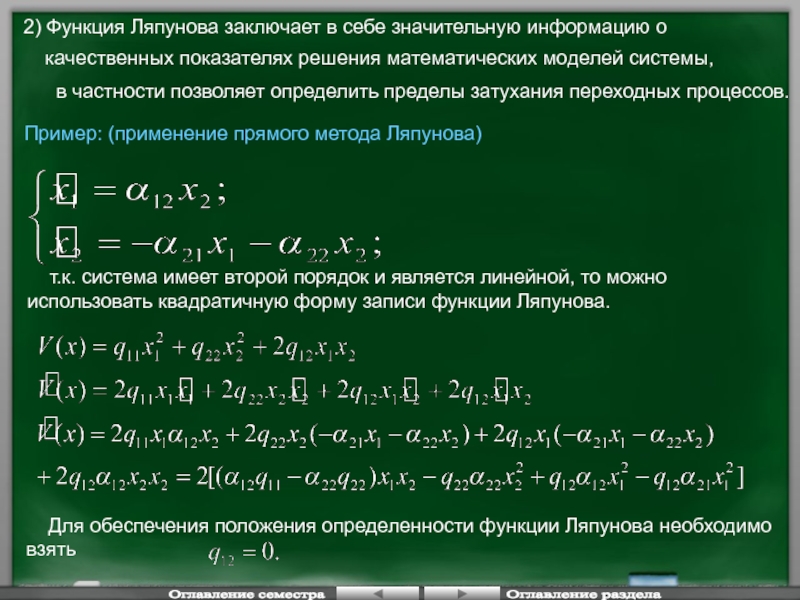
Слайд 1212) Функция Ляпунова заключает в себе значительную информацию о
качественных
в частности позволяет определить пределы затухания переходных процессов.
Пример: (применение прямого метода Ляпунова)
т.к. система имеет второй порядок и является линейной, то можно использовать квадратичную форму записи функции Ляпунова.
Для обеспечения положения определенности функции Ляпунова необходимо взять
Оглавление семестра
Оглавление раздела
Слайд 122
Для обеспечения отрицательной определенности производной функции
Ляпунова
которые мы имеем:
(но дополнительным условием нужно, чтобы
- положительно)
(*.3) – условие обеспечения устойчивости для системы второго порядка.
Оглавление семестра
Оглавление раздела
Слайд 123
Математическое описание и исследование дискретно-непрерывных систем управления.
Интенсивное развитие
Общие сведения о дискретно-непрерывных системах.
Оглавление семестра
Оглавление раздела
Слайд 124 Таким образом промышленная цифровая система управления всегда содержит непрерывный
ДНСУ (дискретно-непрерывная система управления) такая система содержит хотя бы один преобразователь аналогового сигнала в дискретную форму.
Устройства, с помощью которых аналоговый сигнал преобразуется в дискретный называются квантователями. Процесс преобразования называется квантованием.
Квантование бывает трех типов:
1) по уровню;
2) по времени;
3) смешанное.
По форме представления квантованного сигнала в дискретном виде различают:
1) импульсный;
2) релейный;
3)цифровой.
При этом импульсное квантование связано с квантованием по времени, релейное - по уровню, смешанное - с цифровым.
Оглавление семестра
Оглавление раздела
Слайд 125
Иногда смешанное квантование приводит к тому, что после импульсного
Поскольку квантование производится через некоторые переменные или постоянные промежутки времени, то квантованный сигнал представляется последовательностью импульсов прямоугольной формы.
Формирование дискретного сигнала осуществляется посредством пропускания непрерывного сигнала через ключ, который периодически, с тактом квантования Т (период), замыкается на время τ, которое называется длительностью импульса.
Одним из основных параметром дискретного сигнала является скважность:
Оглавление семестра
Оглавление раздела
0
0
Слайд 126
Любой из параметров импульсной последовательности порознь или вместе может
Если длительность импульса существенно меньше Т, то последовательность импульсов xd(t) можно рассматривать как дискретный сигнал.
Ключ действует как идеальный квантователь
Оглавление семестра
Оглавление раздела
0
0
Слайд 127
Причины построения дискретно-непрерывных систем управления:
1)Появление ЭВМ и
2)Повышенная чувствительность, высокая надежность, отсутствие дрейфа, высокая помехоустойчивость по сравнению аналоговыми, кроме того, небольшие габариты и масса, низкая стоимость и удобство при программировании.
3)Экономичность, связанная с высокой гибкостью по сравнению с аналоговыми регуляторами, заключающаяся в изменении программно-цифрового сигнала или адаптации к характеристикам цифрового управления без каких-либо изменений в аппаратных средствах.
4)Возможность работы в режиме разделения времени (позволяет по одному и тому же каналу передавать несколько различных сигналов).
5)В период между моментами квантования дискретная система движется как разомкнутая, что упрощает анализ системы, особенно для нелинейных систем.
В период размыкания системы возможно решение различных фоновых задач на ЭВМ.
Оглавление семестра
Оглавление раздела
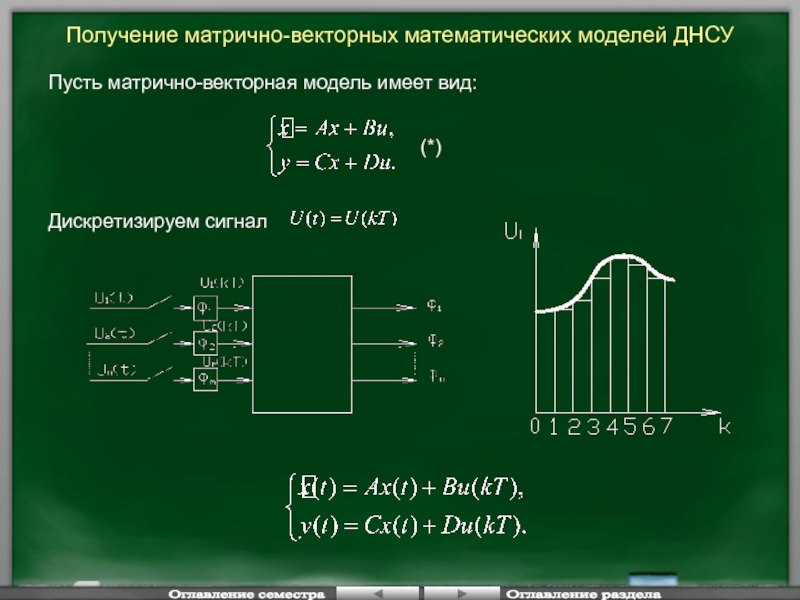
Слайд 128Получение матрично-векторных математических моделей ДНСУ
Пусть матрично-векторная модель имеет вид:
(*)
Оглавление семестра
Оглавление раздела
Слайд 129
Последнее выражение по математической записи ничем не отличаются от
Оглавление семестра
Оглавление раздела
Слайд 130
Заменить в уравнении (*) на дискретную переменную простой подстановкой
- системная матрица дискрено-непрерывного объекта.
Элементы этой матрицы являются зависимыми от периода дискретизации.
Оглавление семестра
Оглавление раздела
Слайд 131
Пример:
Дана переходная матрица непрерывной системы.
Уравнения наблюдений,
Для упрощения математической записи ДНСУ часто применяют прием нормирования по независимому аргументу.
(***)
Система записана для стационарного объекта. Если объект не стационарный, то матрицы входящие в систему становятся зависимыми от момента времени K.
Оглавление семестра
Оглавление раздела
Слайд 132
Если состояния и движения системы описываются уравнением (***), то,
Для определения переходной матрицы дискретной системы можно применить итерационную процедуру, поскольку первое уравнение в системе (***) записано для момента времени K и K+1, где К – произвольный текущий момент, то его можно сдвинуть на любое число позиций в левой и правой части одновременно.
Переходные уравнения состояния ДНС
Устойчивость ДНСУ будет определяться тем: затухающая, ограниченная или расходящаяся функция матрицы перехода.
Поскольку в последнем выражении системная матрица AT может быть представлена в любой эквивалентной форме, то ее можно привести к диагональной форме.
Оглавление семестра
Оглавление раздела
Слайд 133
По диагонали такой матрицы стоят ее собственные числа, а
При этом условии все элементы матрицы будут стремиться к 0, а сама матрица - к нулевой матрице. Если какой - то из корней = 1, то получится ограниченная матрица (астатическая система). При наличии хотя бы одного корня больше 1 соответствующий элемент матрицы при стремится к ∞, и вся матрица оказывается неограниченной.
Пример:
Непрерывная динамическая система имеет системную матрицу вида:
Необходимо определить системную матрицу ДНСУ.
Для решения задачи необходимо определить переходную матрицу непрерывной системы и осуществив дискретизацию получить дискретную матрицу .
Оглавление семестра
Оглавление раздела
Слайд 134
Преобразуем системную матрицу к диагональной форме записи.
Будем
Объект квантованный с периодом является устойчивым в дискретной области, т.к. диагональные элементы системной матрицы меньше 1, а объект с - устойчивым в дискретной области, но на границе устойчивости, т.к. диагональные элементы стремятся к единице.
Оглавление семестра
Оглавление раздела
Слайд 135
Вычисление переходной матрицы состояния ДНСУ
Вычисление переходной матрицы дискретных состояний
Метод основан на теореме Гамильтона-Кэли:
Любая квадратная матрица удовлетворяет собственному характеристическому уравнению.
,т.е. для вычисления переходной матрицы на N-ном шаге достаточно иметь степени матриц вплоть до N-ной.
продолжая эту процедуру можно получить матрицу любой степени.
Оглавление семестра
Оглавление раздела
Слайд 136
Эквивалентные преобразования матрично-векторных моделей
линейных ДНСУ:
Преобразование дискретной модели из
При этой форме записи, каждая переменная состояния в k+1 момент времени зависит только в k-ый момент времени и от управления.
1) Каноническая форма записи
Оглавление семестра
Оглавление раздела
Слайд 137
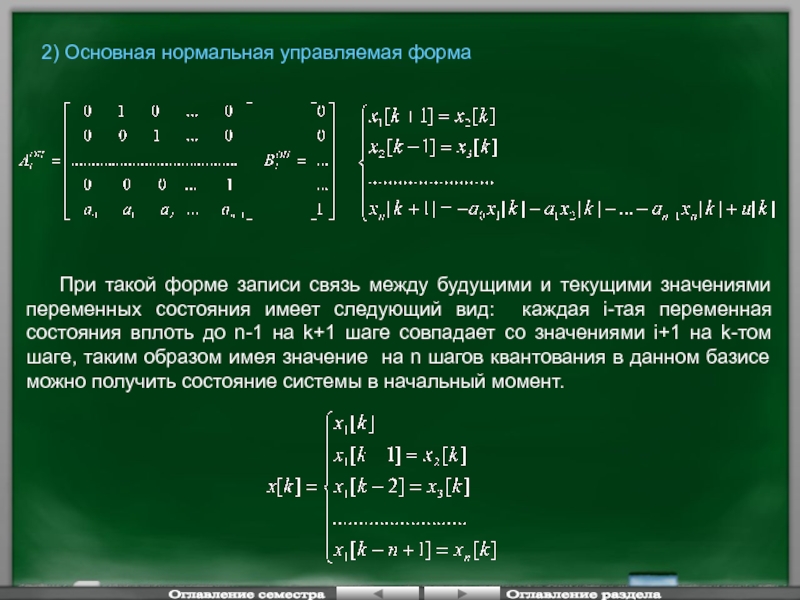
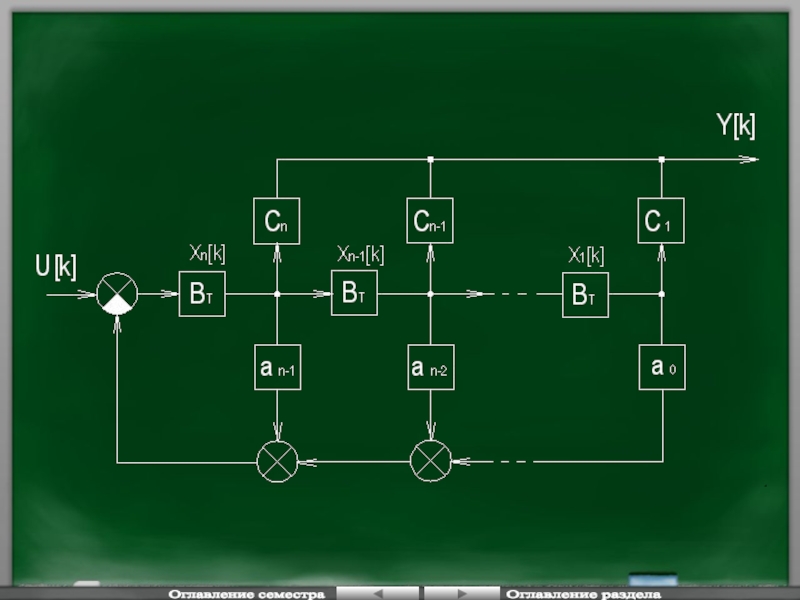
2) Основная нормальная управляемая форма
При такой форме записи связь
Оглавление семестра
Оглавление раздела
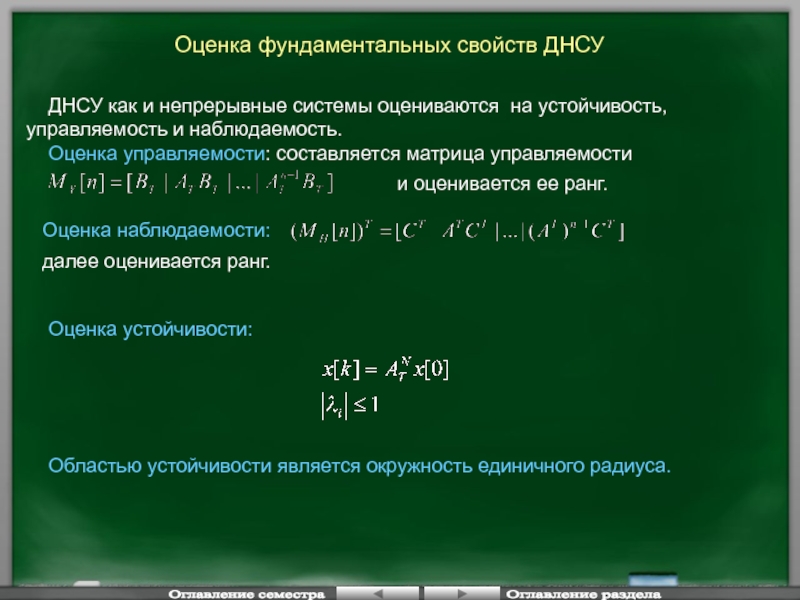
Слайд 139Оценка фундаментальных свойств ДНСУ
ДНСУ как и непрерывные системы оцениваются
Оценка управляемости: составляется матрица управляемости
и оценивается ее ранг.
Оценка наблюдаемости:
далее оценивается ранг.
Областью устойчивости является окружность единичного радиуса.
Оценка устойчивости:
Оглавление семестра
Оглавление раздела
Слайд 140Математические модели процессов в ДНСУ
Основной особенностью математического описания процессов,
Понятие идеального квантователя:
Наиболее распространенным математическим методом описания дискретных функций является замена последовательности импульсов, чаще всего прямоугольных, полученных при квантовании решетчатой функции состоящей из идеальных импульсов. Если продолжительность замыкания ключа значительно меньше периода Т, то импульсы дискретной последовательности можно приближенно заменить идеальными импульсами идеальной площади:
Решетчатая функция физически нереализуема.
Введение идеального квантователя позволяет значительно упростить математический аппарат.
Пусть , тогда сигнал
Оглавление семестра
Оглавление раздела
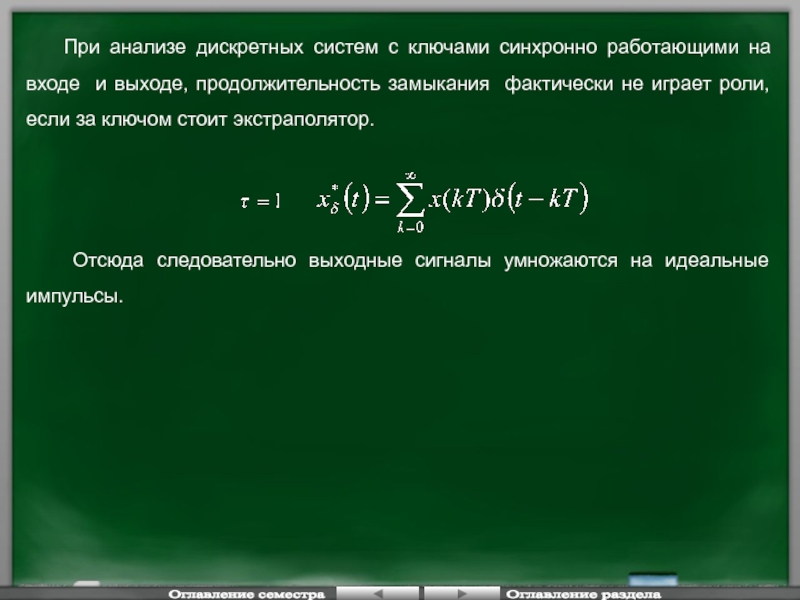
Слайд 141 При анализе дискретных систем с ключами синхронно работающими на
Отсюда следовательно выходные сигналы умножаются на идеальные импульсы.
Оглавление семестра
Оглавление раздела
Слайд 142 Применение преобразования Лапласа для анализа дискретных сигналов
Преобразуем по
Очевидно, что подынтегральное выражение не равно 0 при , при этом остается постоянным.
Из выражя видно, что функция является периодической с частотой повторенияени
Теорема прерывания:
Если непрерывный сигнал имеет ограниченную полосу частот, его преобразование Фурье удовлетворяет условиям:
Оглавление семестра
Оглавление раздела
0
0
Слайд 143 Если же частота квантования не достаточно велика, т.е.
Таким образом, в спектре квантованного сигнала по сравнению со спектром непрерывного появляются дополнительные высокочастотные составляющие.
Операция восстановления исходного сигнала по изображению может быть выполнена без ошибки только при условии:
Предположим, что сигнал подвергается квантованию с малым периодом Т, после чего аппроксимируется последовательностью . Если величина Т достаточно мала, то преобразование Фурье распадается на “основной спектр” и совокупность повторяющихся с периодом “дополнительных спектров”.
- теорема о прерывании Котельникова.
В теории цифрового управления частота называется Шенноновской:
определяет полосу пропускания дискретной системы.
Оглавление семестра
Оглавление раздела
0
0
Слайд 144Анализ качества дискретных систем:
Для анализа качества функционирования ДНС
На качество и на фундаментальные свойства ДНС существенно влияет период дискретизации, поэтому выбор периода дискретизации является важным этапом анализа и синтеза ДНСУ.
Анализ качества во временной области:
Замечание: сложность анализа качества ДНСУ состоит в том, что отсутствует информация о поведении системы между тактами квантования, в этих случаях используют модифицированное z – преобразование.
Связь показателей качества ДНСУ с корнями имеет более сложный вид, чем в непрерывном случае.
Оглавление семестра
Оглавление раздела
Слайд 146Выделение области с заданной степенью устойчивости:
Оглавление семестра
Оглавление раздела
0
0


















![ПримерДан объект управленияС=[1 0 0] Необходимо построить МВ ММОглавление семестра Оглавление раздела](/img/tmb/5/415390/d4d0be7e62182b7c03c14c1005f6d45a-800x.jpg)