- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теория автоматического управления. (Часть 1) презентация
Содержание
- 1. Теория автоматического управления. (Часть 1)
- 2. Учебный курс «Теория Автоматического
- 3. Классическая ТАУ Основные понятия и определения
- 5. Математическое описание объектов и систем управления
- 6. Структурные представления и анализ в теории управления
- 7. Временные и частотные характеристики динамических объектов и
- 8. Исследование одноконтурных систем автоматического управления (САУ)
- 9. Синтез САУ методом типовых регуляторов Виды
- 10. Построение областей устойчивости САУ в плоскости
- 11. Оценка качества управления в линейных автоматических системах
- 12. Джеймс Уатт (James Watt) Родился 19 января
- 13. Цель курса ТАУ – ознакомление с принципами
- 14. Управляющее устройство Объект
- 15. Устройство управления - это устройство, в котором
- 16. Пример: Простейшая система автоматического регулирования уровня жидкости
- 17. Общая функциональная структура САУ САУ состоит из
- 18. Фундаментальные принципы управления Два основных принципа: 1.
- 19. Принцип замкнутого управления: ε – ошибка
- 20. Классификация САУ Классификацию САУ можно производить по
- 21. Пример: Построение математической модели объекта управления
- 22. Данная форма записи (Коши) является
- 23. Форма (1) содержала 4 переменных
- 24. Построение математической модели является первым
- 25. Разложение осуществляется по формуле:
- 26. (3) Это вход-выходное дифференциальное
- 27. Применяем преобразование Лапласа к
- 28. Определение передаточной функции по различным каналам исследования.
- 29. Свойства передаточной функции динамического звена. 1) Передаточная
- 31. Элементарная передаточная функция – передаточная
- 32. Типовые (элементарные) динамические звенья. 1) Пропорциональное звено
- 33. Структурные представления и анализ в теории
- 34. Оглавление семестра Оглавление раздела
- 35. Основные типы соединения звеньев в САУ 1)
- 36. Основные правила структурных преобразований
- 37. Замечание: Не всякая структурная схема упрощается
- 38. Временные и частотные характеристики динамических объектов и
- 39. Специальные функции. Оглавление семестра
- 40. 2) Единичное, ступенчатое воздействие (функция Хевисайда) Самая распространенная функция в ТАУ.
- 41. 3) Линейно-возрастающая функция 4) Параболическое воздействие Оглавление семестра Оглавление раздела
- 42. Функцию, описывающую
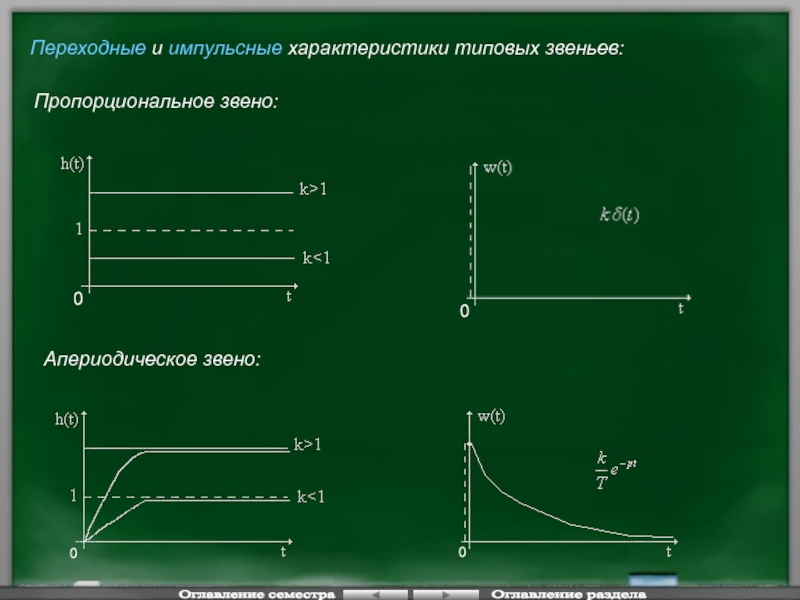
- 44. Переходные и импульсные характеристики типовых звеньев: Пропорциональное
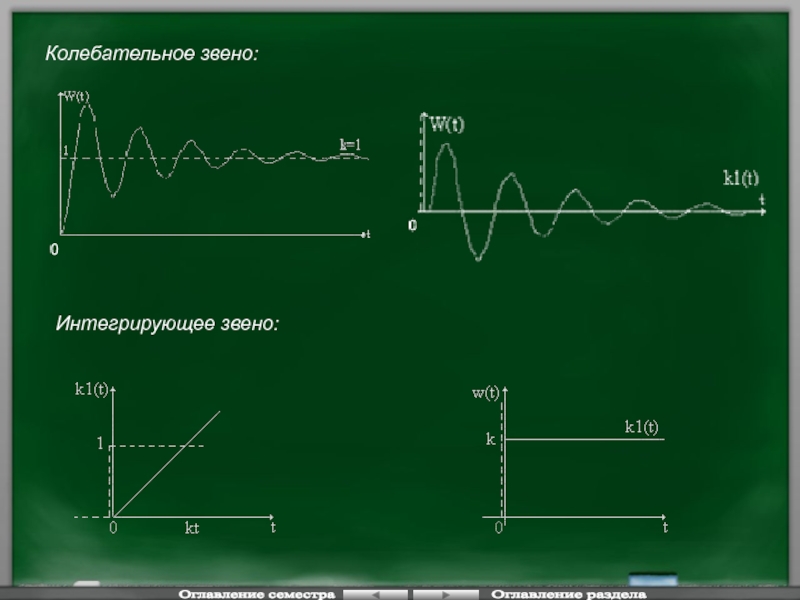
- 45. Колебательное звено: Интегрирующее звено: Оглавление семестра Оглавление раздела
- 46. Дифференцирующее звено: Пропорционально - дифференцирующее 1го порядка:
- 47. Частотные характеристики линейных динамических звеньев и систем.
- 48. ВЧХ МЧХ ВЧХ -
- 49. Для построения частотных характеристик используется диапазон частот
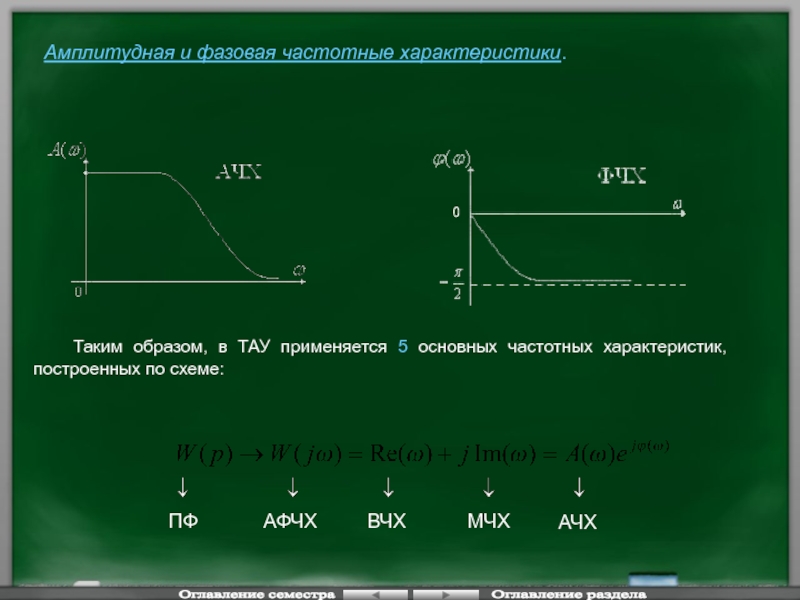
- 51. Амплитудная и фазовая частотные характеристики. Таким образом,
- 52. Частотные характеристики любого линейного
- 53. 1. Пропорциональное звено АФЧХ ВЧХ ФЧХ МЧХ АЧХ
- 54. 2. Интегрирующее звено АФЧХ ВЧХ ФЧХ МЧХ АЧХ
- 55. 3. Дифференциирующее звено АФЧХ ВЧХ ФЧХ МЧХ АЧХ
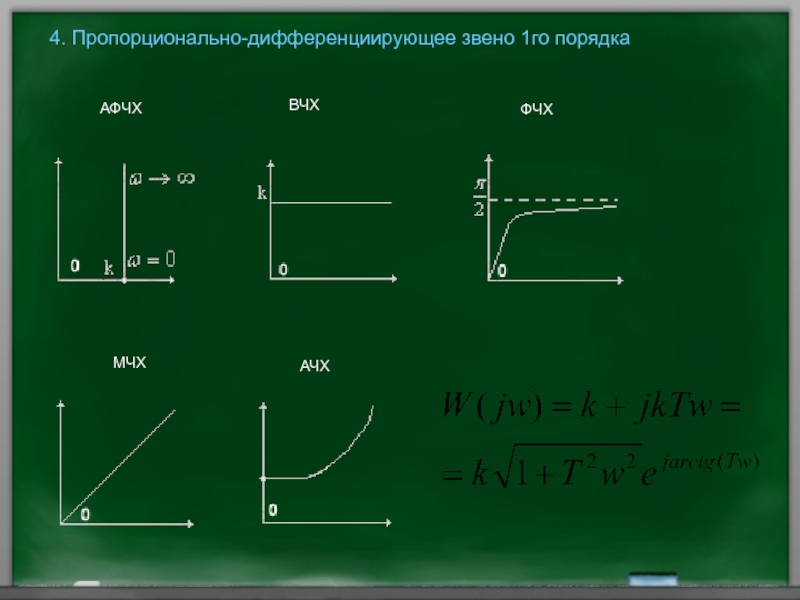
- 56. 4. Пропорционально-дифференциирующее звено 1го порядка АФЧХ ВЧХ ФЧХ МЧХ АЧХ
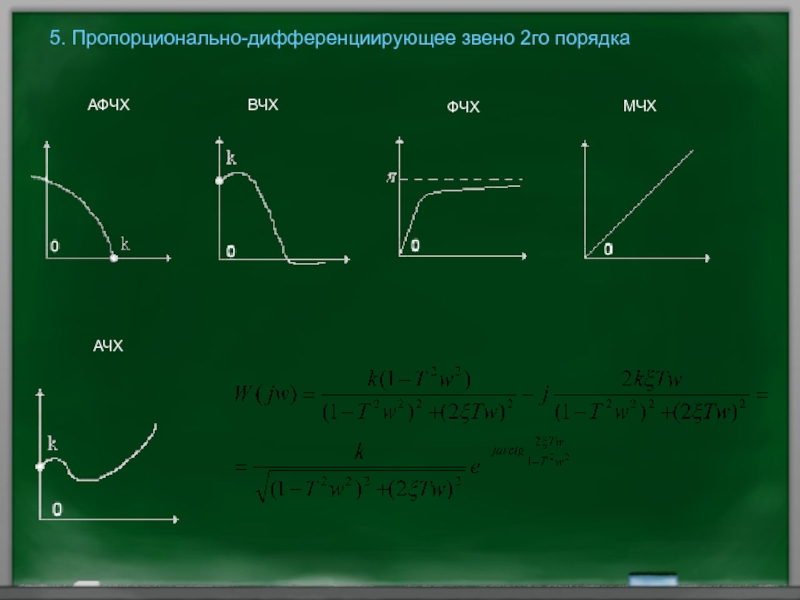
- 57. 5. Пропорционально-дифференциирующее звено 2го порядка АФЧХ ВЧХ ФЧХ МЧХ АЧХ
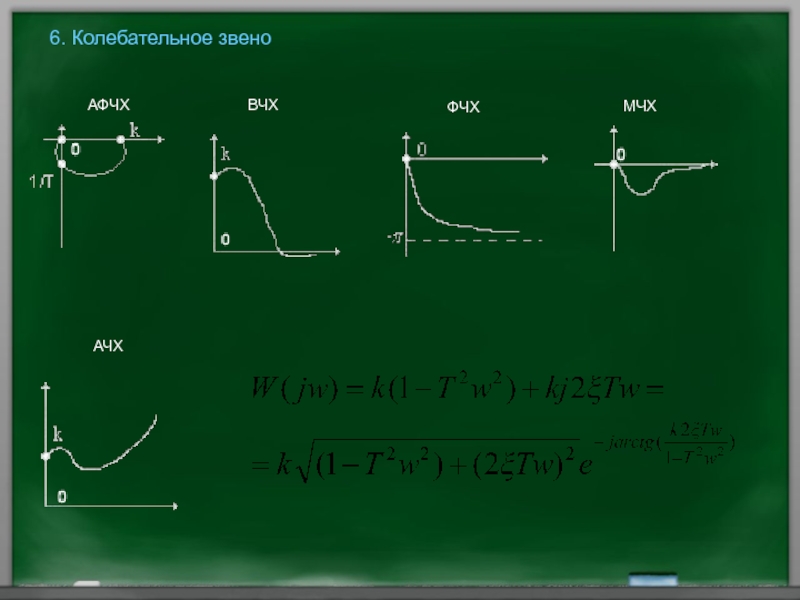
- 58. 6. Колебательное звено АФЧХ ВЧХ ФЧХ МЧХ АЧХ
- 59. Оглавление семестра Оглавление раздела
- 60. Логарифмические частотные характеристики динамических объектов и
- 61. Оглавление семестра Оглавление раздела
- 62. Все звенья
- 63. ЛАЧХ ЛФЧХ ПЗ ИЗ ДЗ Оглавление семестра Оглавление раздела
- 64. ЛАЧХ ЛФЧХ ПД1 КЗ ПД2 Оглавление семестра Оглавление раздела
- 65. Построение логарифмических частотных характеристик (ЛЧХ) сложных динамических
- 66. При построении ЛАЧХ: Правильно строить низкочастотную асимптоту;
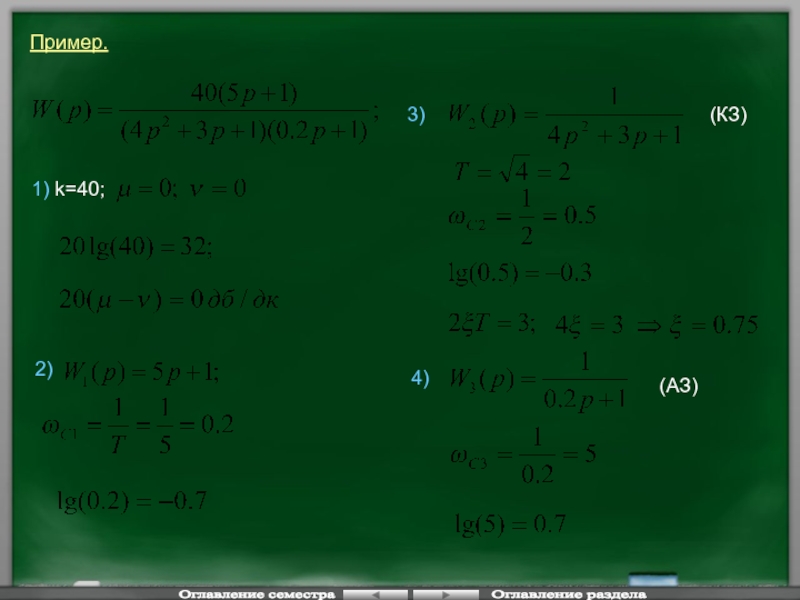
- 67. Пример. 1) k=40;
- 68. Оглавление семестра Оглавление раздела
- 69. Нетиповые динамические звенья. Нетиповые звенья получены на
- 70. Неминимально-фазовое звено – звено, в
- 71. г) Нетиповые звенья, описываемые трансцендентной функцией (звено
- 72. Исследование замкнутых одноконтурных систем автоматического управления.
- 73. Понятие устойчивости. Методы оценки устойчивости объектов и
- 74. Качественная оценка характеристического полинома. Необходимое условие устойчивости
- 75. В 1878 году английский математик Раус предложил
- 76. Правило определения устойчивости: Если все диагональные миноры
- 77. Во всех частотных критериях при оценке устойчивости
- 78. Для устойчивости объекта или системы необходимо и
- 79. По сути, это частный случай принципа аргумента,
- 80. Пример: неустойчивые Пример: на границе устойчивости Оглавление семестра Оглавление раздела
- 81. Модифицированный критерий Михайлова. Обычно применяется при построении
- 82. Критерий Найквиста: Оценка устойчивости замкнутых систем по
- 83. Годограф, изображающий характеристическую функцию, совпадает с годографом
- 84. Аналитическая трактовка критерия Найквиста.
- 85. Для того, чтобы замкнутая система была устойчивой,
- 86. 2) Разомкнутая система обладает астатизмом первого порядка
- 87. 4) Разомкнутая система содержит неустойчивое звено Оглавление семестра Оглавление раздела
- 88. Понятие запасов устойчивости замкнутой системы. Критерий Найквиста
- 89. Оглавление семестра Оглавление раздела
- 90. Трактовка критерия Найквиста с использованием ЛЧХ. Применение
- 91. В инженерной практике, в процессе проектирования реальных
- 92. Астатические первого порядка
- 93. Синтез систем автоматического управления методом типовых регуляторов.
- 94. 1) П – пропорциональный регулятор Достоинства: Простота
- 95. 2) И – интегрирующий регулятор (применяется для
- 96. 3) ПИ – пропорционально-интегральный регулятор
- 97. 4) ПД – пропорционально-дифференциальный регулятор Достоинства: Расширяет
- 98. 5) ПИД – пропорционально-интегрально дифференцируемый регулятор Оглавление семестра Оглавление раздела
- 99. Построение областей устойчивости САУ в плоскости
- 100. Однопараметрическое D-разбиение. Исходными данными
- 101. Примечание: для построения параметрического годографа необязательно изменять
- 102. Так как M2 L2 и
- 103. 3) - уравнение особой прямой
- 104. 2. (Для особых прямых) Штриховка особых прямых,
- 105. Пример: Оглавление семестра Оглавление раздела
- 106. Оглавление семестра Оглавление раздела
- 107. Оценка качества управления в линейных автоматических
- 108. Методы оценки качества и виды испытываемых
- 109. Оценка качества системы управления по виду переходного
- 110. - (показатель колебательности) Оглавление семестра Оглавление раздела
- 111. Построение переходных процессов в САУ. 1) По
- 112. Графики: Интеграл Дюамеля, -
- 113. Аналитические методы анализа частных показателей точности
- 114. Чем больше тем точнее получается
- 115. Свойство преобразования Лапласа: Используя выражения
- 116. 1) Если система является статической, то она
- 117. Для исследования реакции системы на различные виды
- 118. Оглавление семестра Оглавление раздела
- 119. Методы косвенной (приближенной) оценки качества линейных систем.
- 120. Если входным воздействием является ступенчатая функция, у
- 121. Качественная и приближенная количественная оценки переходных процессов
- 122. а) Амплитудных (ось ординат) 2) Изменение масштабов
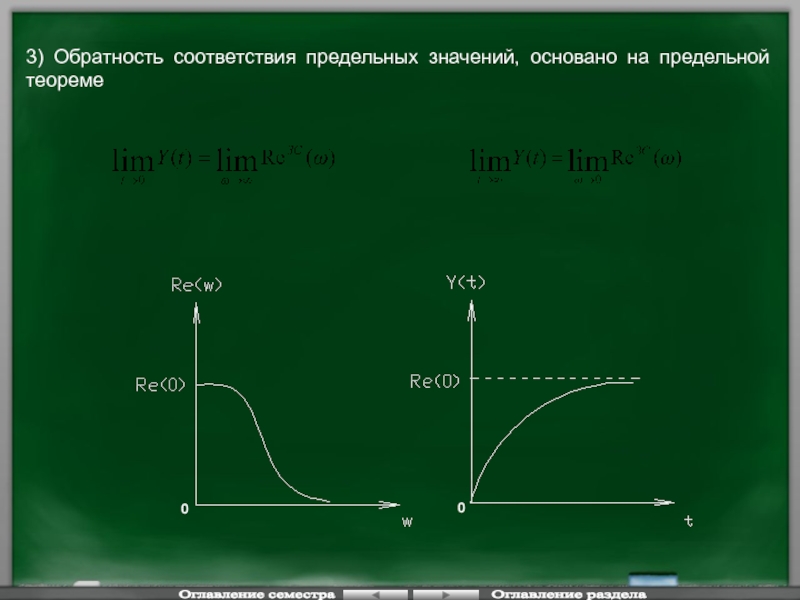
- 123. 3) Обратность соответствия предельных значений, основано на
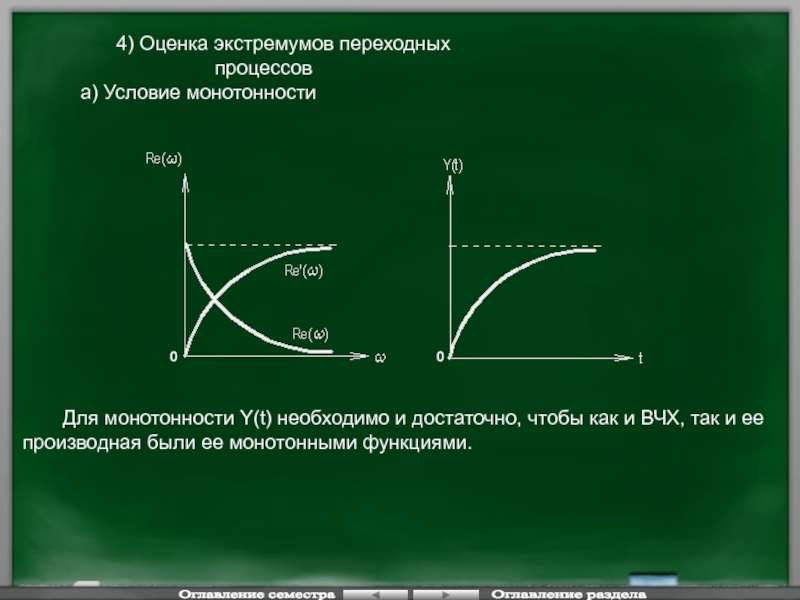
- 124. 4) Оценка экстремумов переходных процессов
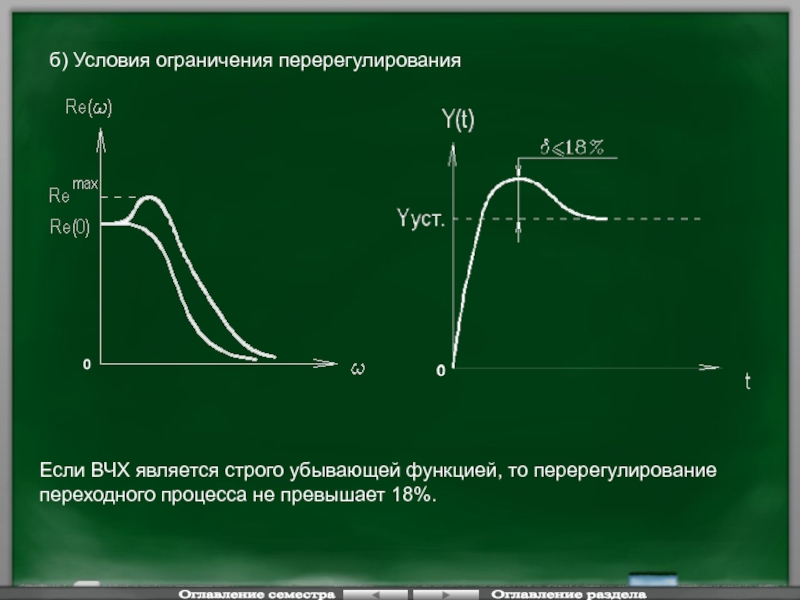
- 125. б) Условия ограничения перерегулирования Если ВЧХ является
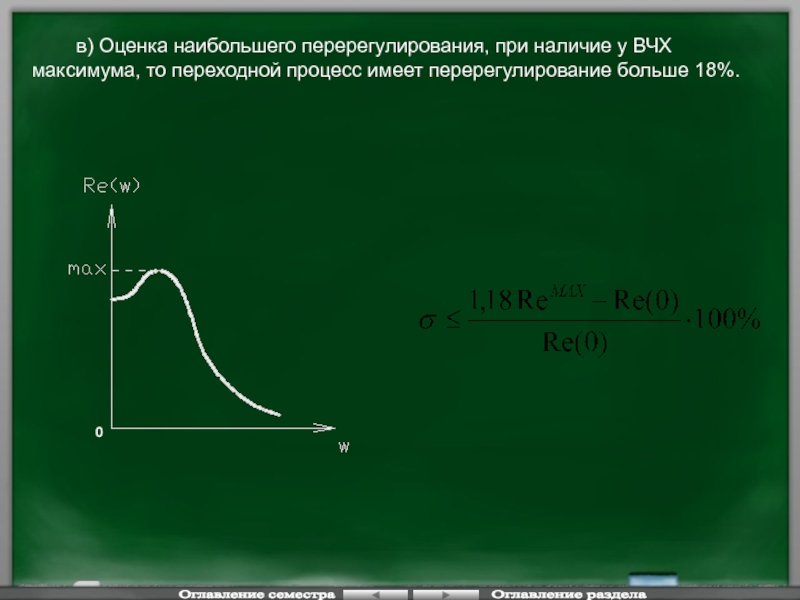
- 126. в) Оценка наибольшего
- 127. 5) Оценка колебательности переходного процесса При наличии
- 128. 6) Условие длительности затухания переходных процессов Если
- 129. Оценка колебательности замкнутой системы по максимуму АЧХ.
- 130. Соответствие показателей колебательности. M – максимум АЧХ
- 131. Оценка быстродействия замкнутой системы по частоте среза
- 132. Корневые методы косвенной оценки качества системы управления.
- 133. Оценка колебательности. (является более удобным) Эти
- 134. Совокупная оценка качества. х1,2 удовлетворяют ограничению
Слайд 2Учебный курс
«Теория Автоматического Управления»
Часть 1
Автор курса – доцент, кандидат технических
Обухов Павел Серафимович
Электронные ресурсы курса находятся на сайтах:
http://de.dstu.edu.ru/, можно зайти также с официального сайта университета http://http://www.http://www.dhttp://www.donstuhttp://www.donstu.ru/ в разделе образование/дистанционное образование - пароль cdodstu
http://www.dstu-app.ru/ и http://www.dstu-smc-app.ru
Слайд 3Классическая ТАУ
Основные понятия и определения теории управления
Математическое описание объектов
Структурные представления и анализ в теории управления
Исследование одноконтурных систем автоматического управления (САУ)
Синтез САУ методом типовых регуляторов
Построение областей устойчивости САУ в плоскости их параметров
Оценка качества управления в линейных автоматических системах
Временные и частотные характеристики динамических объектов и систем
Слайд 4
Основные понятия и определения теории управления:
Общая
Фундаментальные принципы управления
Классификация САУ
Основные понятия и определения теории управления
Оглавление семестра
Джеймс Уатт
Слайд 5Математическое описание объектов и систем управления
Вход - выходные формы математического
объектов и систем управления
Типовые (элементарные) динамические звенья
Свойства передаточной функции динамического звена
Оглавление семестра
Основные понятия и определения
Определение передаточной функции
Слайд 6Структурные представления и анализ в теории управления
Основные типы соединения звеньев
Основные правила структурных преобразований
Основные понятия и определения
Оглавление семестра
Слайд 7Временные и частотные характеристики динамических объектов и систем
Специальные функции
Частотные
Частотные характеристики типовых звеньев
Логарифмические частотные характеристики динамических объектов и систем
Построение логарифмических частотных характеристик (ЛЧХ) сложных динамических звеньев
Нетиповые динамические звенья
Оглавление семестра
Основные понятия и определения
Переходные и импульсные переходные характеристики
ЛАЧХ и ЛФЧХ типовых звеньев
Слайд 8Исследование одноконтурных
систем автоматического управления (САУ)
Алгебраические критерии оценки устойчивости
Частотные
Понятие инженерных запасов
Понятие устойчивости
Оглавление семестра
Основные понятия и определения
Качественная оценка
Слайд 9Синтез САУ методом типовых регуляторов
Виды регуляторов:
Пропорциональный
Интегрирующий
Пропорционально – дифференциальный
Пропорционально – интегрально - дифференциальный
Оглавление семестра
Слайд 10Построение областей устойчивости САУ
в плоскости их параметров
Однопараметрическое D-разбиение
Двухпараметрическое
Основные понятия и определения
Оглавление семестра
Слайд 11Оценка качества управления в линейных автоматических системах
Основные понятия и определения
Прямые методы:
Исследование точности установившихся режимов воспроизведения методом коэффициентов ошибок
Косвенные (приближенные) методы
Оценка колебательности замкнутой системы по максимуму АЧХ
Оценка быстродействия замкнутой системы по частоте среза ЛАЧХ разомкнутой системы
Оглавление семестра
Корневые методы косвенной оценки качества системы управления
Оценка по переходному процессу
Слайд 12Джеймс Уатт (James Watt)
Родился 19 января 1736 г (1736-1819), выдающийся шотландский
Слайд 13 Цель курса ТАУ – ознакомление с принципами построения систем автоматического управления
Управление – целенаправленное воздействие на что-либо.
Управление является автоматическим, если оно осуществляется
без вмешательства человека, с помощью специальных технических средств.
Разработка общих принципов создания таких устройств является задачей ТАУ.
Основные понятия и определения курса ТАУ
Оглавление семестра
Оглавление раздела
Слайд 14
Управляющее устройство
Объект управления
V (F)
Z (G)
U
Y
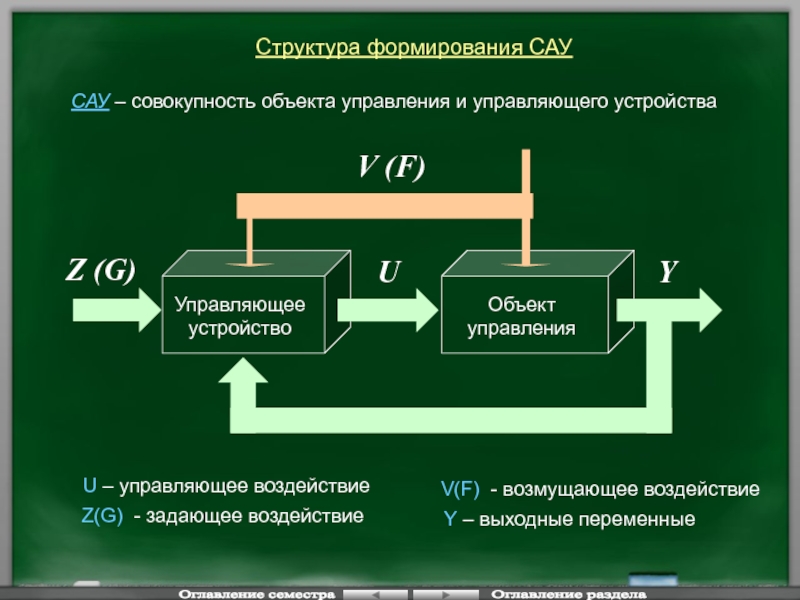
Структура формирования САУ
САУ – совокупность объекта управления
U – управляющее воздействие
Z(G) - задающее воздействие
V(F) - возмущающее воздействие
Y – выходные переменные
Оглавление семестра
Оглавление раздела
Слайд 15 Устройство управления - это устройство, в котором вырабатываются воздействия, называемые управляющими.
Объект
Все переменные можно разделить на две группы:
внутренние и внешние.
Назначение САУ состоит в обеспечении с возможно большей точностью определенной заранее предписанной взаимосвязи управляемых величин Y с задающими воздействиями Z и более полном подавлении влияния возмущающих воздействий и помех V, если они есть.
Внешние переменные - такие переменные, которые могут меняться независимо от состояния объекта и влиять на процессы в нем протекающие.
Оглавление семестра
Оглавление раздела
Внутренние переменные - такие переменные, которые характеризуют технологию протекающих в объекте или системе процессов, то есть его состояние (обозначается X).
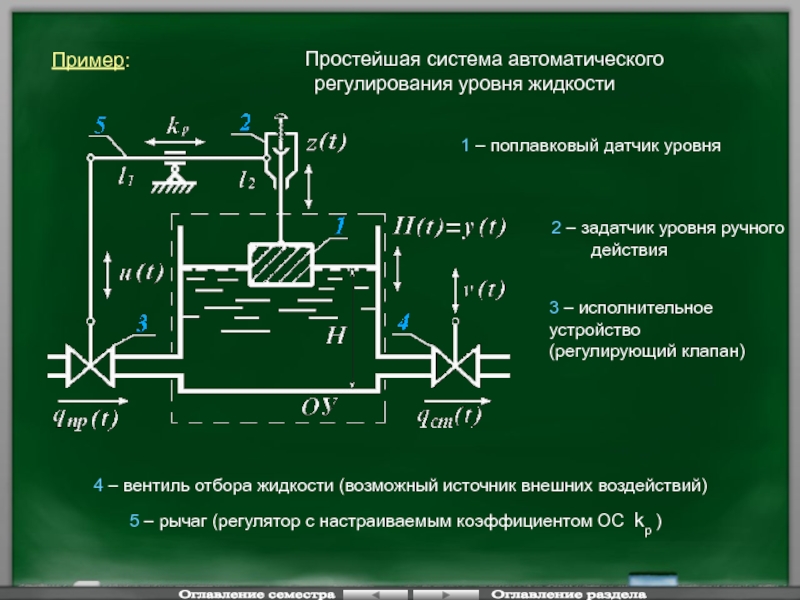
Слайд 16Пример:
Простейшая система автоматического регулирования уровня жидкости
1 – поплавковый датчик уровня
2 –
действия
3 – исполнительное устройство (регулирующий клапан)
4 – вентиль отбора жидкости (возможный источник внешних воздействий)
5 – рычаг (регулятор с настраиваемым коэффициентом ОС kp )
Оглавление семестра
Оглавление раздела
Слайд 17Общая функциональная структура САУ
САУ состоит из следующих основных частей:
К УЧ
- КСЛУ - комплекс средств локального управления;
- КСУУ - комплекс средств усиления управляющих сигналов;
- УВК - управляющий вычислительный комплекс.
- НЧ САУ - неизменяемая часть САУ
- УЧ САУ - управляющая часть САУ
К НЧ САУ относятся:
- непосредственно сам ОУ;
- КСВО - комплекс средств воздействия на ОУ (рег.клапан 3);
- КИИС - комплекс информационно-измерительных средств
Оглавление семестра
Оглавление раздела
Слайд 18Фундаментальные принципы управления
Два основных принципа:
1. Принцип разомкнутого управления
(управление по внешнему
2. Принцип замкнутого управления
(управление по отклонению)
Принцип разомкнутого управления может реализоваться в двух видах:
- управление по заданию
- управление по возмущению
Достоинства: - прямой характер управления (быстродействие)
- простота
- надежность
Недостатки: - низкая точность (большое количество неконтролируемых
воздействий)
- нестационарность характеристик объектов управления
- громоздкость управляющего устройства при большом количестве внешних воздействий
Оглавление семестра
Оглавление раздела
Слайд 19Принцип замкнутого управления:
ε – ошибка управления или регулирования (ε ?
Сумматор – устройство сравнения сигналов
Недостатки: - более низкое быстродействие
- склонность замкнутых систем к автоколебаниям, связанная с процессом циркулирования управляющей информации по замкнутому контуру
Достоинства: - универсальный характер управления
- принципиальная независимость результатов управления от количества значений внешних воздействий
- высокая точность
Комбинированное управление – симбиоз разомкнутой и замкнутой
системы управления
Оглавление семестра
Оглавление раздела
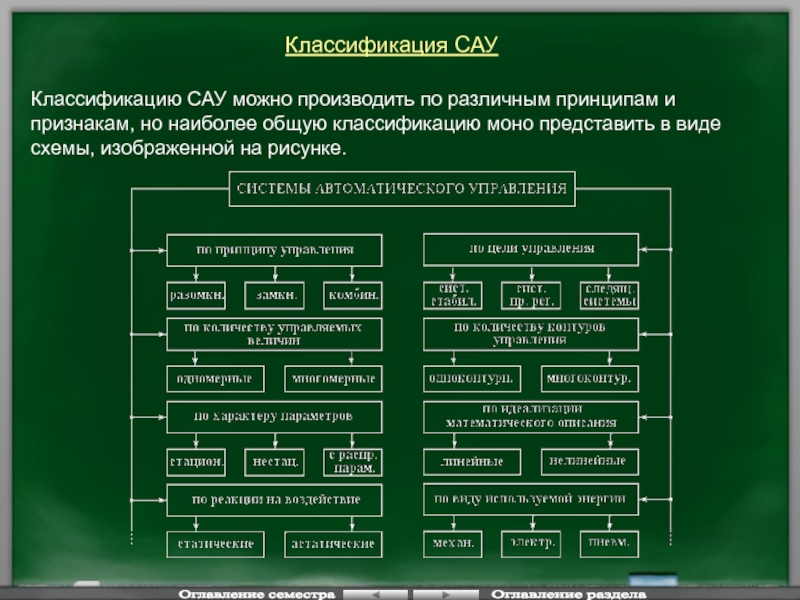
Слайд 20Классификация САУ
Классификацию САУ можно производить по различным принципам и признакам, но
Оглавление семестра
Оглавление раздела
Слайд 21Пример: Построение математической модели объекта управления
Эти переменные полностью характеризуют фундаментальные свойства
(1)
Математическое описание объектов и систем
управления.
Оглавление семестра
Оглавление раздела
Слайд 22 Данная форма записи (Коши) является основной для построения матрично-векторной
Для получения вход-выходной формы записи, выразим во 2-ом уравнении х1 и подставим в 1-ое; кроме того найдем 1-ую и 2-ую производную х1 и подставим. Далее преобразуем, чтобы входы остались справа, а выходная переменная х2 (скорость баржи) осталась слева. И получится одно уравнение четвертого порядка, которое называется вход-выходным описанием объекта.
(2)
Вывод: при получении математического описания данного объекта управления был последовательно получен ряд форм моделей от системы 4-х уравнений 1-го порядка до одного уравнения 4-го порядка.
Оглавление семестра
Оглавление раздела
Слайд 23 Форма (1) содержала 4 переменных состояния, которые, при сделанных
Форма (2) получена исключением переменных состояний и приведения к одному уравнению, разрешенному относительно одной интересующей нас переменной, являющейся выходом объекта. При этом все входные воздействия были сохранены.
Форма (1) является более полной по сравнению с формой (2).
Форма (2) менее полная, чем исходная, но ее использование облегчает и упрощает многие преобразования и анализ. Она используется в классической теории управления.
Математической моделью является выражение или система выражений, в которых буквенными символами обозначены реальные физические переменные, изменяющиеся в процессе функционирования объекта, а символами математических операций отображаются реальные физические законы преобразования этих переменных в объекте.
В результате изменение состояния переменных в реальном объекте и решение математической модели этого объекта должны давать численно совпадающие результаты. Степень совпадения этих результатов указывает на степень адекватности математической модели ее техническому оригиналу.
Оглавление семестра
Оглавление раздела
Слайд 24 Построение математической модели является первым и очень важным этапом
Основной трудностью использования дифференциальной формы описания объектов и систем является сложность и громоздкость решения ДУ, особенно нелинейных и в частных производных. А подавляющее большинство технических объектов описывается именно такими уравнениями. Поэтому такие математической модели стараются упростить. Самым простой способ упрощения является процедура линеаризации, так как для линейных ДУ в математике и для линейных объектов в ТАУ существуют хорошо развитые операторные методы анализа и синтеза.
Для того, чтобы линеаризовать нелинейную ММ, необходимо, чтобы линеаризуемся функция была дифференцируема на всем протяжении (не имела разрывов и неоднозначности). Тогда ее можно разложить в ряд Тейлора в окрестности произвольно выбранной точки (для САУ - это обычно положение равновесия - ).
- положение равновесия
Оглавление семестра
Оглавление раздела
Слайд 25Разложение осуществляется по формуле:
- отклонения переменных состояния от
- сумма членов, которые содержат различные производные во второй и более высших степенях и смешанных производных от функции в соответствующем аргументе (этой частью разложения обычно пренебрегают).
Оглавление семестра
Оглавление раздела
Слайд 26
(3)
Это вход-выходное дифференциальное уравнение, в котором u,v является входами,
При исследовании линейных систем широко применяются так называемые операторные методы. Операции дифференцирования и интегрирования заменяются алгебраическими операциями умножения и деления за счет применения специальных преобразований, что резко упрощает все процедуры преобразования и исследования математических моделей объектов и систем.
Из операторных методов наиболее известны:
1) Преобразование Лапласа:
Вход-выходные формы
математического описания объектов и систем управления.
Математическое описание одномерных объектов и систем.
2) Преобразование Фурье:
Оглавление семестра
Оглавление раздела
Слайд 27
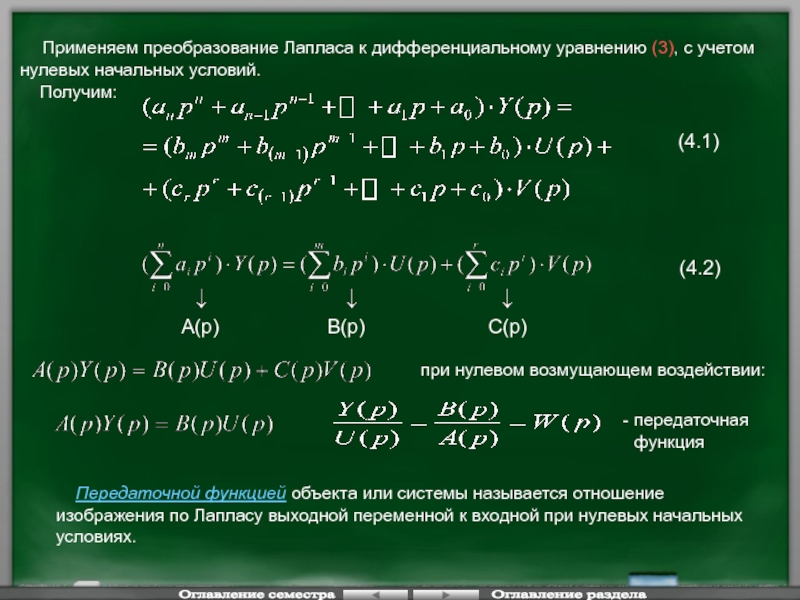
Применяем преобразование Лапласа к дифференциальному уравнению (3), с учетом
Получим:
(4.1)
(4.2)
A(p)
B(p)
C(p)
при нулевом возмущающем воздействии:
передаточная
функция
Передаточной функцией объекта или системы называется отношение изображения по Лапласу выходной переменной к входной при нулевых начальных условиях.
Оглавление семестра
Оглавление раздела
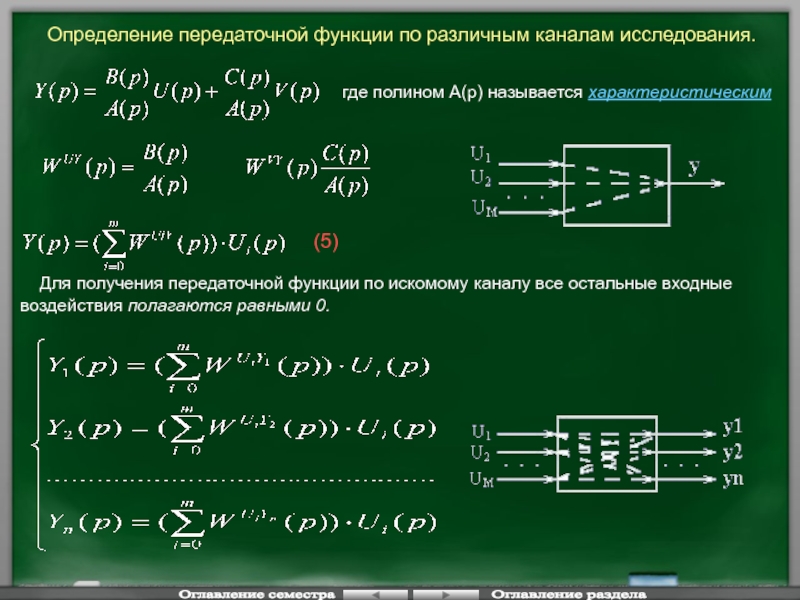
Слайд 28Определение передаточной функции по различным каналам исследования.
где полином А(р) называется
(5)
Для получения передаточной функции по искомому каналу все остальные входные воздействия полагаются равными 0.
Оглавление семестра
Оглавление раздела
Слайд 29Свойства передаточной функции динамического звена.
1) Передаточная функция линейного звена является дробно-рациональной,
2) Для физической реализуемости (реальные объекты и системы) порядок полинома в числителе не должен превышать порядок полинома в знаменателе.
3) Передаточная функция объекта по каналам для одной и той же выходной переменной имеет в знаменателе один и тот же полином, который называется характеристическим, т.к. его структура и параметры определены фундаментальными свойствами объекта.
Свойства полиномов числителя и знаменателя передаточной функции:
- количество нулевых корней в полиноме
- количество вещественных корней
ks - количество пар комплексно - сопряженных корней
Оглавление семестра
Оглавление раздела
Слайд 30
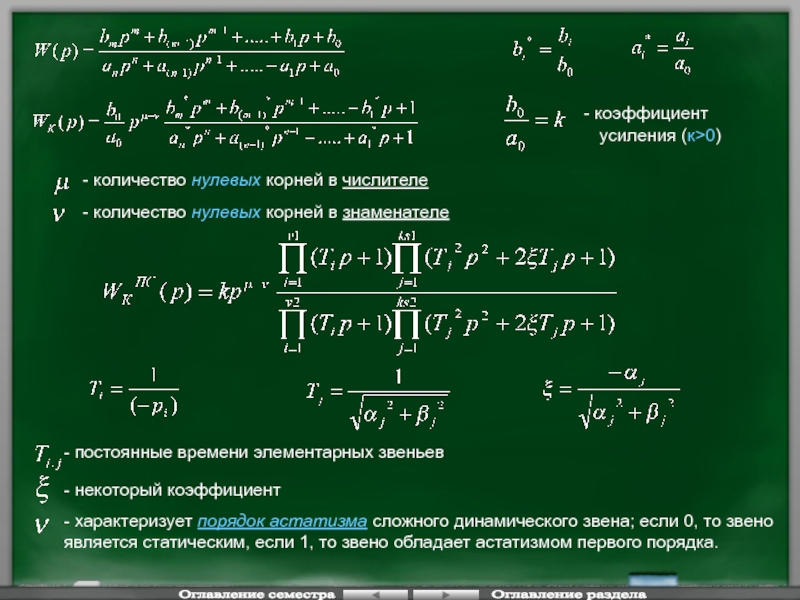
- количество нулевых корней в
- количество нулевых корней в знаменателе
коэффициент
усиления (к>0)
- постоянные времени элементарных звеньев
- некоторый коэффициент
- характеризует порядок астатизма сложного динамического звена; если 0, то звено является статическим, если 1, то звено обладает астатизмом первого порядка.
Оглавление семестра
Оглавление раздела
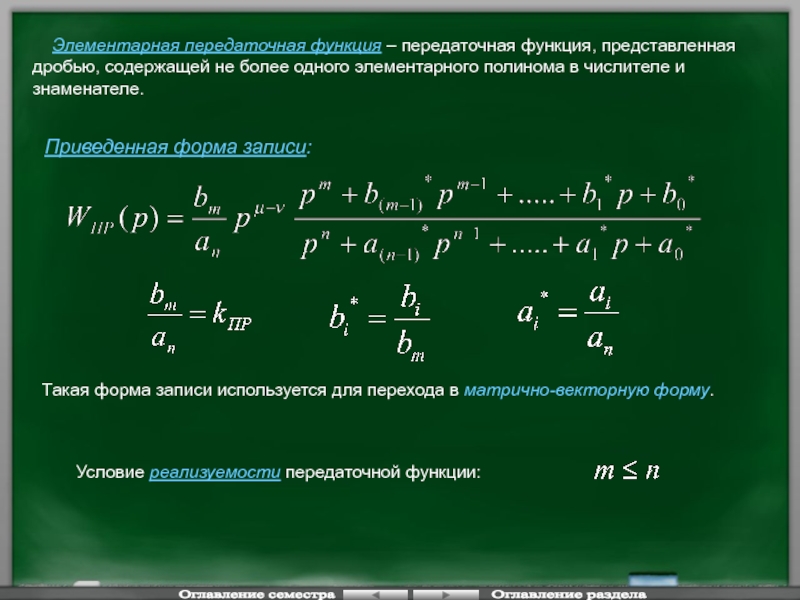
Слайд 31 Элементарная передаточная функция – передаточная функция, представленная дробью, содержащей
Приведенная форма записи:
Такая форма записи используется для перехода в матрично-векторную форму.
Условие реализуемости передаточной функции:
Оглавление семестра
Оглавление раздела
Слайд 32Типовые (элементарные) динамические звенья.
1) Пропорциональное звено (ПЗ)
2) Дифференцирующее звено (ДЗ)
3)
4) Пропорционально-дифференцирующее звено (ПД)
5) Апериодическое звено (АЗ)
6) Пропорционально-дифференцирующее звено 2-го порядка (ПД2)
7) Колебательное звено (КЗ)
Звенья 1,3,5,7 – являются физически реализуемыми, т.е. реальными, а 2,4,6 – физически не реализуемыми т.е. идеальными.
(но Т< Оглавление семестра Оглавление раздела
Слайд 33Структурные представления и анализ
в теории управления
В структурных схемах переменные –
Структурные схемы являются самой наглядной формой математического представления объектов и систем.
Структурной схемой в ТАУ называется графическое изображение математической модели автоматической системы в виде соединения звеньев.
Разбиение сложной передаточной функции на элементарные составляющие (типовые звенья) не является чисто математическим приемом. Любое реальное устройство физически или технологически может быть разбито на совокупность динамических звеньев низкого порядка. Переход от реальных объектов (элементов) САУ к их математическим моделям позволяет абстрагироваться от физически принципов систем, поэтому структурная схема является основой универсальных методов анализа и синтеза математических систем.
Оглавление семестра
Оглавление раздела
Слайд 35Основные типы соединения звеньев в САУ
1) Параллельное соединение
2)
3) Обратная связь
Оглавление семестра
Оглавление раздела
Слайд 37Замечание:
Не всякая структурная схема упрощается до типовой. Рассмотренными выше методами преобразования,
Суть этих преобразований сводится к целенаправленному переносу элементов структурных схем (звеньев, узлов, сумматор) друг через друга, но так чтобы результирующая передаточная функция не изменилась.
Оглавление семестра
Оглавление раздела
Слайд 38Временные и частотные характеристики динамических объектов и систем.
Временные характеристики.
Понятие
(динамическое звено)
Система называется детерминированной, если каждому входному сигналу X(t) отвечает один, единственный сигнал Y(t). В недетерминированных системах входному сигналу соответствует несколько возможных выходных сигналов, каждый из которых имеет определенную вероятность появления.
Система называется стационарной, если взаимосвязь между входом и выходом не зависит от времени. В стационарной системе величина и вид выходного сигнала не зависит от входного сигнала.
Временные характеристики в ТАУ применяют с целью изучения поведения автоматических систем во временной области, когда о свойствах системы можно судить на любом этапе управления по ее реакции на входное воздействие.
В качестве входных воздействий могут выступать как известные, так и случайные функции, в ТАУ используются так называемые специальные функции.
Оглавление семестра
Оглавление раздела
Слайд 39Специальные функции.
Оглавление семестра
Оглавление раздела
1) Дельта-функция
Дельта-функция - это импульс бесконечно
Слайд 402) Единичное, ступенчатое воздействие (функция Хевисайда)
Самая распространенная функция в ТАУ.
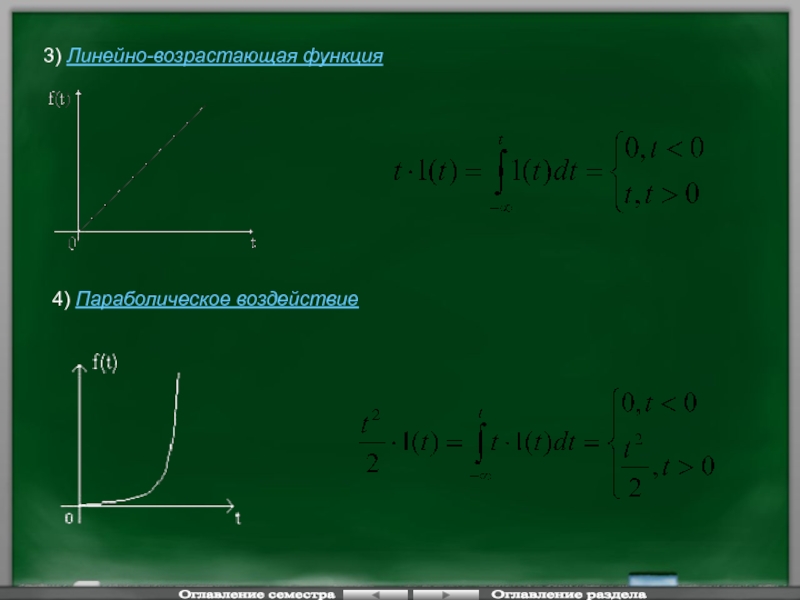
Слайд 413) Линейно-возрастающая функция
4) Параболическое воздействие
Оглавление семестра
Оглавление раздела
Слайд 42
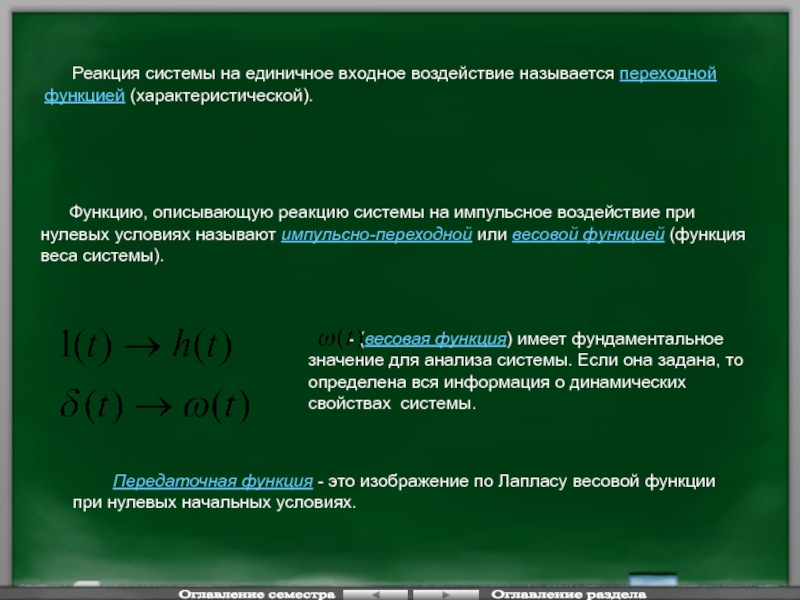
Функцию, описывающую реакцию системы на импульсное воздействие при
- (весовая функция) имеет фундаментальное значение для анализа системы. Если она задана, то определена вся информация о динамических свойствах системы.
Оглавление семестра
Оглавление раздела
Реакция системы на единичное входное воздействие называется переходной функцией (характеристической).
Передаточная функция - это изображение по Лапласу весовой функции при нулевых начальных условиях.
Слайд 43
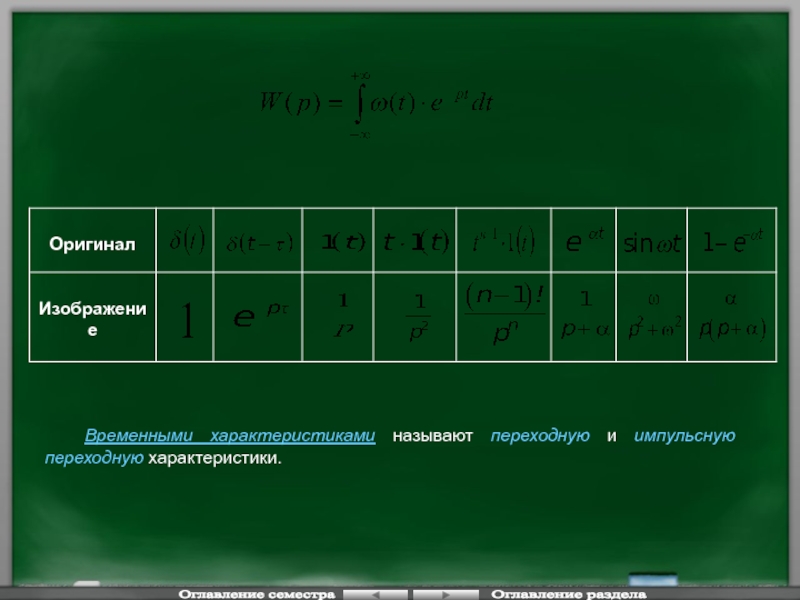
Временными характеристиками называют переходную и импульсную переходную характеристики.
Оглавление семестра
Оглавление раздела
Слайд 44Переходные и импульсные характеристики типовых звеньев:
Пропорциональное звено:
Апериодическое звено:
Оглавление семестра
Оглавление раздела
Слайд 46Дифференцирующее звено:
Пропорционально - дифференцирующее 1го порядка:
Оглавление семестра
Оглавление раздела
Слайд 47Частотные характеристики линейных динамических звеньев и систем.
- по ней строится
АФЧХ – амплитудно-фазовая частотная характеристика
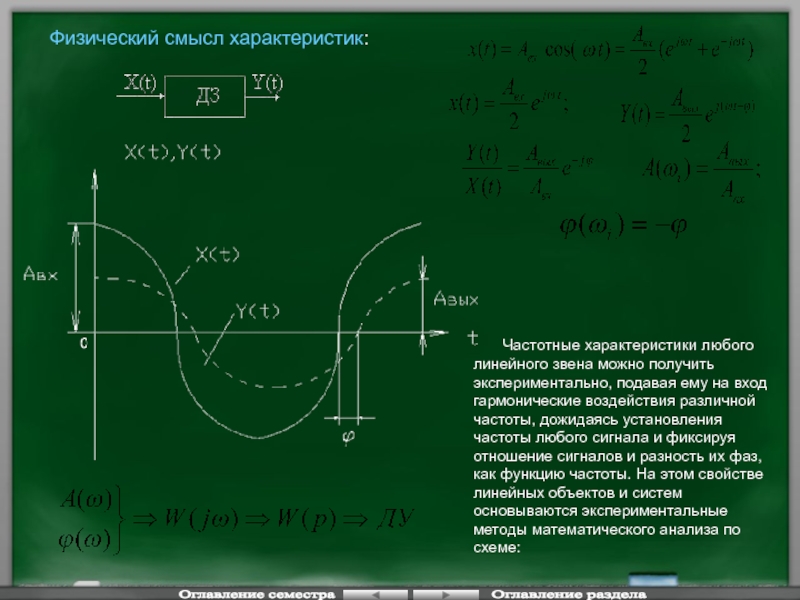
Наряду с преобразованием Лапласа для математического описания, преобразования и исследования линейных объектов и систем используется преобразование Фурье, которое можно рассматривать как частный случай преобразования Лапласа, когда произвольная, абстрактная независимая переменная p рассматривается как мнимая конкретная переменная jw которую называют мнимой частотой.
Переход от операторной записи к частотной форме осуществляется простой подстановкой вместо аргумента p аргумент jw.
Оглавление семестра
Оглавление раздела
Слайд 48ВЧХ
МЧХ
ВЧХ - вещественная частотная
МЧХ - мнимая частотная
характеристика
ВЧХ – Re(w), МЧХ – Im(w)
Оглавление семестра
Оглавление раздела
АЧХ - амплитудно - частотная
характеристика
ФЧХ - фазо - частотная
характеристика
ВЧХ
- АЧХ
- ФЧХ
Слайд 49Для построения частотных характеристик используется диапазон частот от 0 до
Оглавление
Оглавление раздела
Слайд 51Амплитудная и фазовая частотные характеристики.
Таким образом, в ТАУ применяется 5 основных
Оглавление семестра
Оглавление раздела
ВЧХ
МЧХ
АЧХ
ПФ
АФЧХ
Слайд 52 Частотные характеристики любого линейного звена можно получить экспериментально,
Физический смысл характеристик:
Оглавление семестра
Оглавление раздела
Слайд 59Оглавление семестра
Оглавление раздела
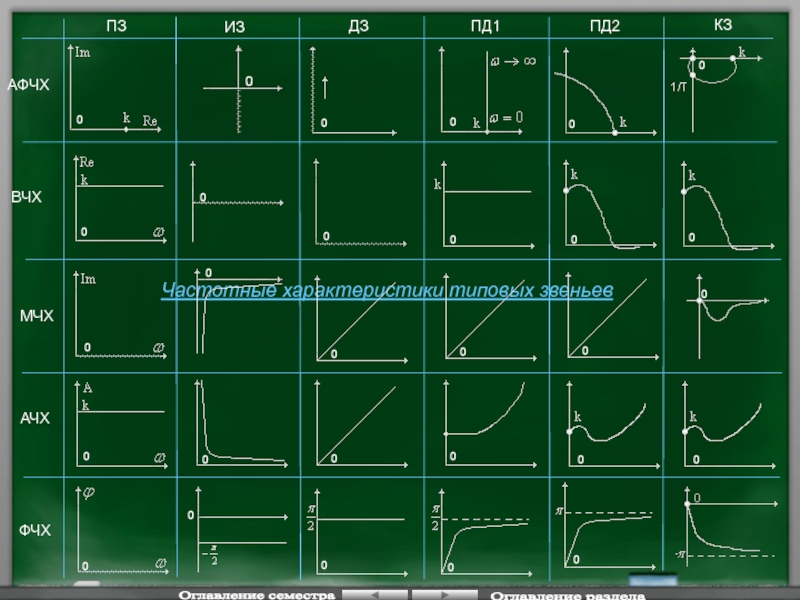
АФЧХ
ВЧХ
МЧХ
АЧХ
Частотные характеристики типовых
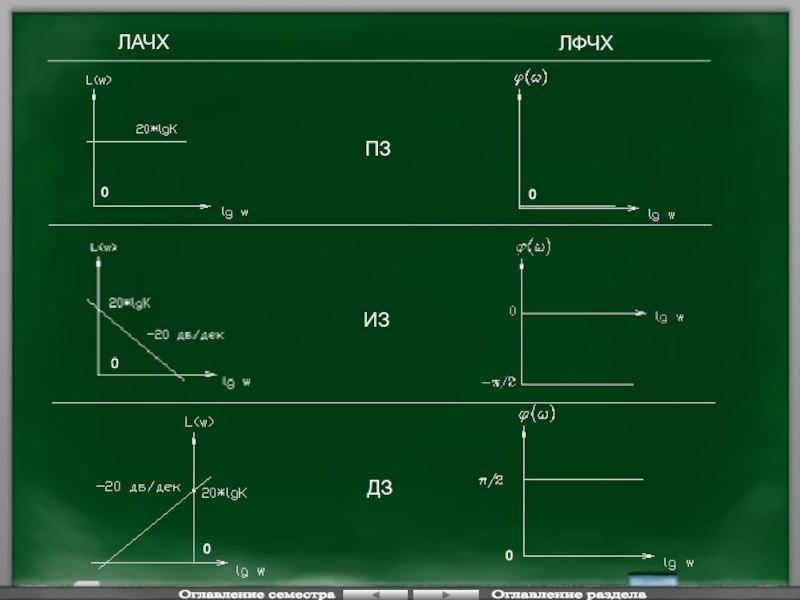
ПЗ
ИЗ
ДЗ
ПД1
ПД2
КЗ
ФЧХ
Слайд 60Логарифмические частотные характеристики
динамических объектов и систем.
В ТАУ применяется две логарифмические
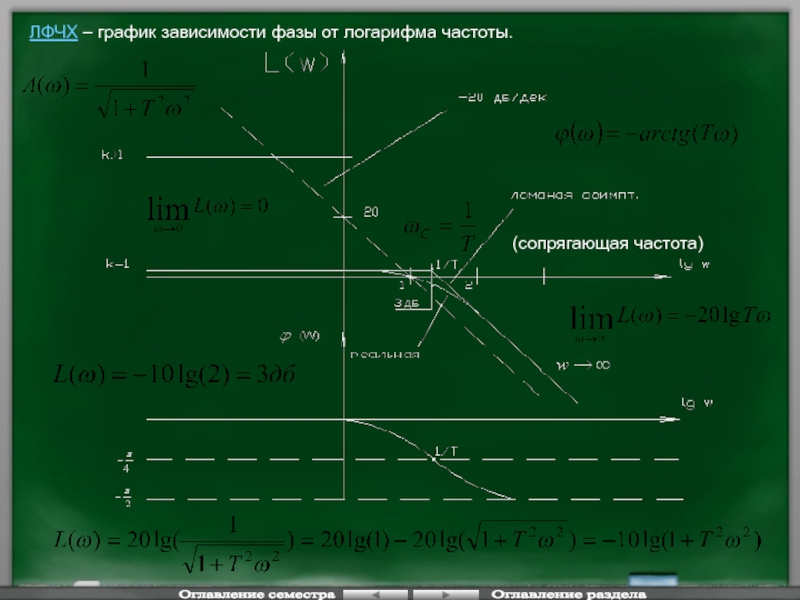
ЛАЧХ – график зависимости логарифма амплитуды от логарифма частоты.
Логарифм измеряется в децибелах по оси ординат и в декадах по оси абсцисс.
Декадой называется интервал, на котором частота изменяется в 10 раз.
Оглавление семестра
Оглавление раздела
Слайд 61Оглавление семестра
Оглавление раздела
ЛФЧХ – график зависимости фазы от логарифма
(сопрягающая частота)
Слайд 62
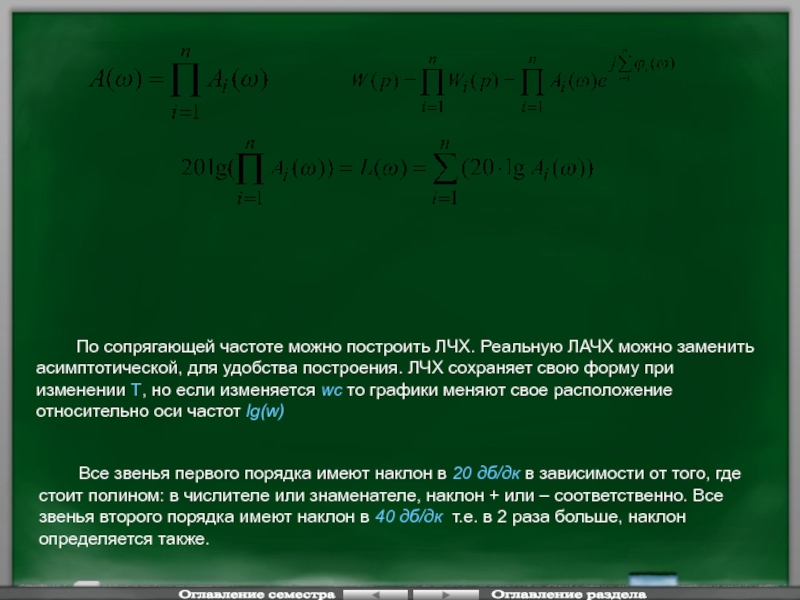
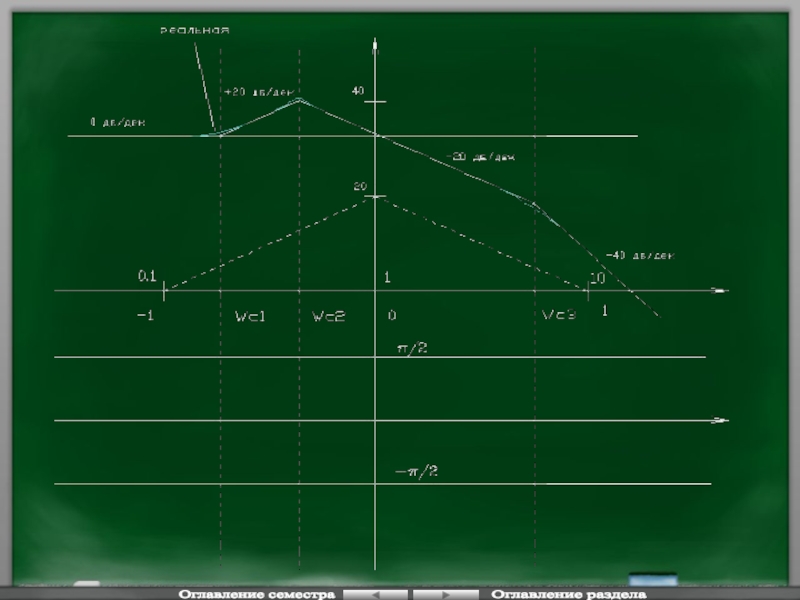
Все звенья первого порядка имеют наклон в 20 дб/дк в зависимости
По сопрягающей частоте можно построить ЛЧХ. Реальную ЛАЧХ можно заменить асимптотической, для удобства построения. ЛЧХ сохраняет свою форму при изменении Т, но если изменяется wc то графики меняют свое расположение относительно оси частот lg(w)
Оглавление семестра
Оглавление раздела
Слайд 65Построение логарифмических частотных характеристик (ЛЧХ) сложных динамических звеньев.
Построение ЛФЧХ сложного динамического
Построение ЛАЧХ сложного динамического звена.
Исходными данными для построения этих характеристик является передаточная функция объекта или системы, преобразуемая к канонической последовательно-структурированной форме записи.
Сначала строится ЛФЧХ элементарных динамических звеньев, входящих в сложное по отдельности. После этого они суммируются и формируют ЛФЧХ сложного звена.
При этом процедура графического сложения необязательна и неэффективна с временной точки зрения, т.к. возможно последовательное построение графика асимптотической характеристики путем поворота асимптот в сопрягающих частотах при движении по оси частот слева направо.
Оглавление семестра
Оглавление раздела
Слайд 66При построении ЛАЧХ:
Правильно строить низкочастотную асимптоту;
При построении двигаться строго слева направо.
Правило
Таким образом на оси частот откладывается точка соответствующая нулю, на оси ординат откладывается 20*lg(k) и через эту точку проводится линия с наклоном
Правило построения среднечастотной асимптоты:
Оглавление семестра
Оглавление раздела
1. Определяются сопрягающие частоты всех элементарных звеньев, входящих в сложное
2. Далее они располагаются на оси абсцисс в порядке возрастания, через эти частоты проводятся ординаты пунктиром. Построенная низкочастотная асимптота проводится до точки пересечения с первой ординатой – это будет первая точка поворота ЛАЧХ
3. Далее определяется звено, которое соответствует этой частоте, и в соответствии с его характеристиками изменяется наклон ЛАЧХ сложного звена
4. ЛАЧХ продолжается до точки пересечения со следующей ординатой
Правило построения высокочастотной асимптоты:
Последняя построенная асимптота продолжается до бесконечности.
Слайд 69Нетиповые динамические звенья.
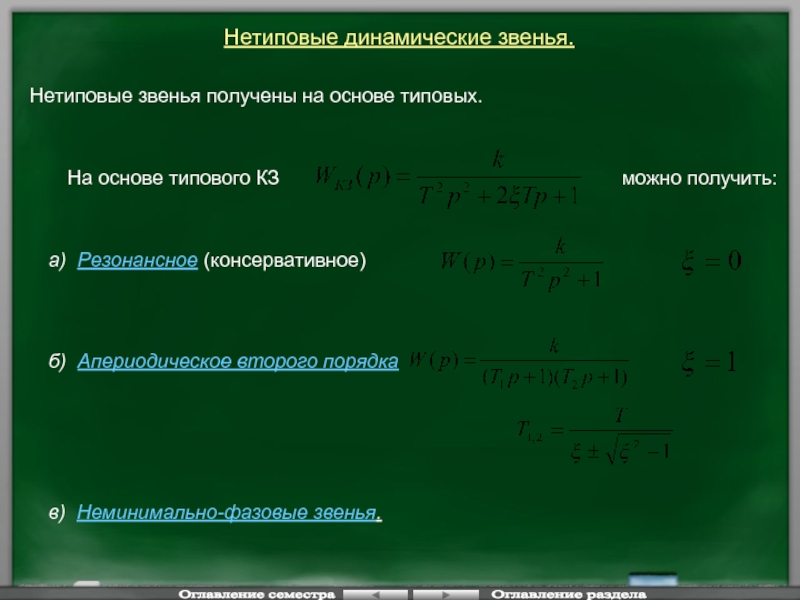
Нетиповые звенья получены на основе типовых.
На основе типового КЗ
можно
а) Резонансное (консервативное)
б) Апериодическое второго порядка
в) Неминимально-фазовые звенья.
Оглавление семестра
Оглавление раздела
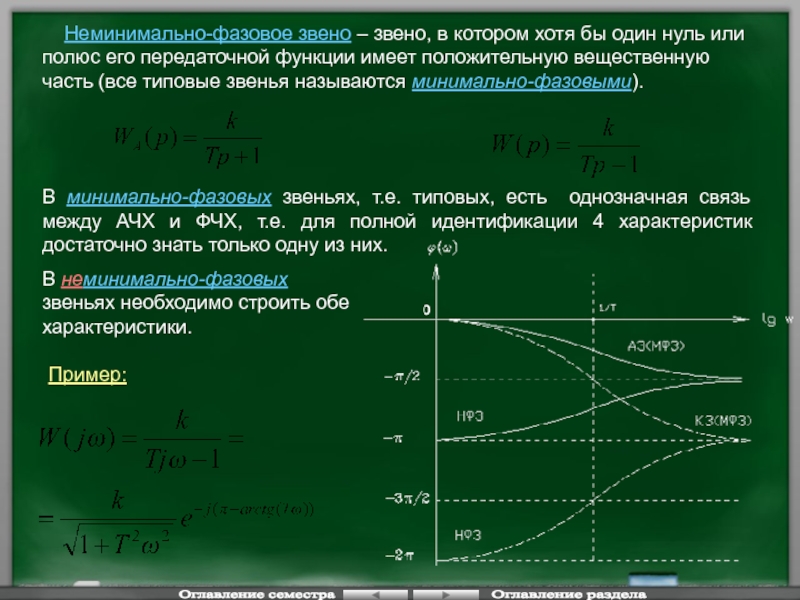
Слайд 70 Неминимально-фазовое звено – звено, в котором хотя бы один
В минимально-фазовых звеньях, т.е. типовых, есть однозначная связь между АЧХ и ФЧХ, т.е. для полной идентификации 4 характеристик достаточно знать только одну из них.
В неминимально-фазовых звеньях необходимо строить обе характеристики.
Пример:
Оглавление семестра
Оглавление раздела
Слайд 71г) Нетиповые звенья, описываемые трансцендентной функцией (звено чистого запаздывания).
Звено чистого запаздывания
Оглавление семестра
Оглавление раздела
Явным примером звена чистого запаздывания является конвейер.
Слайд 72Исследование замкнутых одноконтурных систем автоматического управления.
- характеристическая функция.
где S(p) -
разомкнутой системы.
В характеристической функции в числителе стоит характеристический полином замкнутой системы, а в знаменателе характеристический полином разомкнутой системы.
N(p)
Оглавление семестра
Оглавление раздела
Слайд 73Понятие устойчивости.
Методы оценки устойчивости объектов и систем.
Корневой критерий (Ляпунова)
1 – устойчивые корни
2 – нулевой корень
3 – нейтральные корни
4 – неустойчивые корни
Оглавление семестра
Оглавление раздела
Слайд 74Качественная оценка характеристического полинома.
Необходимое условие устойчивости всех корней характеристического полинома:
Все коэффициенты
должны быть одного знака;
2) Характеристический полином должен быть полным, т.е. содержать все ненулевые коэффициенты, т.е. для каждого
Эти же условия для полинома второго порядка являются и достаточными, а для полиномов более высокого порядка они только необходимые.
Все методы оценки устойчивости делятся на 2 основных класса:
а) Алгебраические (с помощью алгебраических вычислений)
б) Частотные (используя частотные характеристики)
Алгебраические критерии:
Льенара-Шипара
Рауса
Гурвица
Оглавление семестра
Оглавление раздела
Слайд 75В 1878 году английский математик Раус предложил критерий:
Исходными данными является характеристический
По критерию Рауса исследуемая система устойчива, если все коэффициенты в первом столбце таблицы Рауса имеют одинаковый знак, если условие не соблюдается, то характеристический полином имеет неустойчивые корни, количество которых равно числу перемен знака. В таблице всегда (n-1) строк.
Критерий Рауса
Критерий Гурвица
В 1895 году новый критерий изобрел немецкий математик Гурвиц.
Для оценки устойчивости также используется характеристический полином. На его основе составлен главный определитель Гурвица
Алгебраические критерии:
Для проверки правильности составления определителя, анализируется главная диагональ, где должны стоять все коэффициенты характеристического полинома от а0 до аn-1
Оглавление семестра
Оглавление раздела
Слайд 76 Правило определения устойчивости: Если все диагональные миноры положительны и а0 тоже,
Правило: Если все коэффициенты характеристического полинома не равны нулю и все главные миноры матрицы Гурвица с четными (нечетными) номерами тоже, то характеристический полином является устойчивым.
Критерий Льенара-Шипара
Оглавление семестра
Оглавление раздела
Слайд 77Во всех частотных критериях при оценке устойчивости используют один и тот
Частотные критерии.
Оглавление семестра
Оглавление раздела
Слайд 78Для устойчивости объекта или системы необходимо и достаточно, чтобы суммарный угол
Оглавление семестра
Оглавление раздела
Слайд 79По сути, это частный случай принципа аргумента, при оценке удобно использовать
Критерий устойчивости Михайлова:
Правило оценки устойчивости:
Для того, чтобы система была устойчива необходимо и достаточно, чтобы годограф начинался на положительной вещественной оси из точки а0 и последовательно против часовой стрелки проходил количество квадрантов, равное размерности системы или степени характеристического полинома.
Пример: устойчивые
Оглавление семестра
Оглавление раздела
Слайд 81Модифицированный критерий Михайлова.
Обычно применяется при построении и анализе годографа Михайлова в
В данном критерии фазовый сдвиг вносимый корнями сохраняется и проходит такое же количество квадрантов как в обычном критерии, а изменяется только модуль, который нормируется в соответствии с коэффициентом стоящим в знаменателе.
Оглавление семестра
Оглавление раздела
Слайд 82Критерий Найквиста: Оценка устойчивости замкнутых систем по разомкнутым
- характеристический полином замкнутой
- характеристический полином разомкнутой системы
Оглавление семестра
Оглавление раздела
Для оценки устойчивости используют АФЧХ разомкнутой системы.
Слайд 83Годограф, изображающий характеристическую функцию, совпадает с годографом АФЧХ разомкнутой системы, если
Таким образом, если из условий устойчивости корней характеристического полинома найти обязательным образом связанные свойства вектора, изображающего характеристическую функцию, то можно по годографу АФЧХ разомкнутой системы судить об устойчивости замкнутой системы.
Для оценки устойчивости можно использовать принцип аргумента, как в критерии Михайлова.
Оглавление семестра
Оглавление раздела
Слайд 84Аналитическая трактовка критерия Найквиста.
Пусть в разомкнутой системе
Оглавление семестра
Оглавление раздела
Слайд 85 Для того, чтобы замкнутая система была устойчивой, необходимо и достаточно, чтобы
Графическая трактовка критерия Найквиста.
Частные случаи применения критерия:
Разомкнутая система является устойчивой
1)
Для устойчивости замкнутой системы необходимо и остаточно, чтобы годограф АФЧХ не охватывал точку с координатами (-1, j0). Для этого применяется эмпирическое правило правой штриховки: на годограф АФЧХ наносится штриховка справа по мере увеличения частоты, если точка (-1 , j0) попадает в область штриховки, значит годограф охватывает ее.
Оглавление семестра
Оглавление раздела
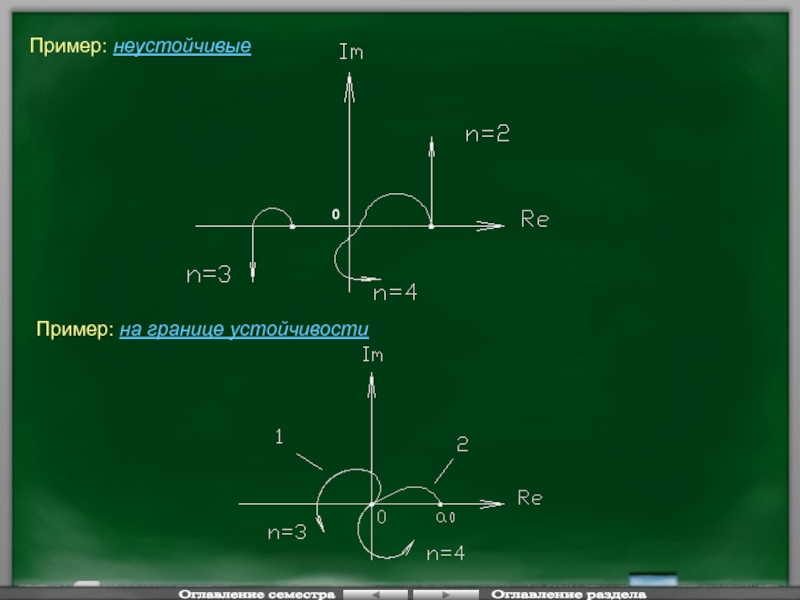
Слайд 862) Разомкнутая система обладает астатизмом первого порядка
1 – устойчива
2 – неустойчива
3)
Оглавление семестра
Оглавление раздела
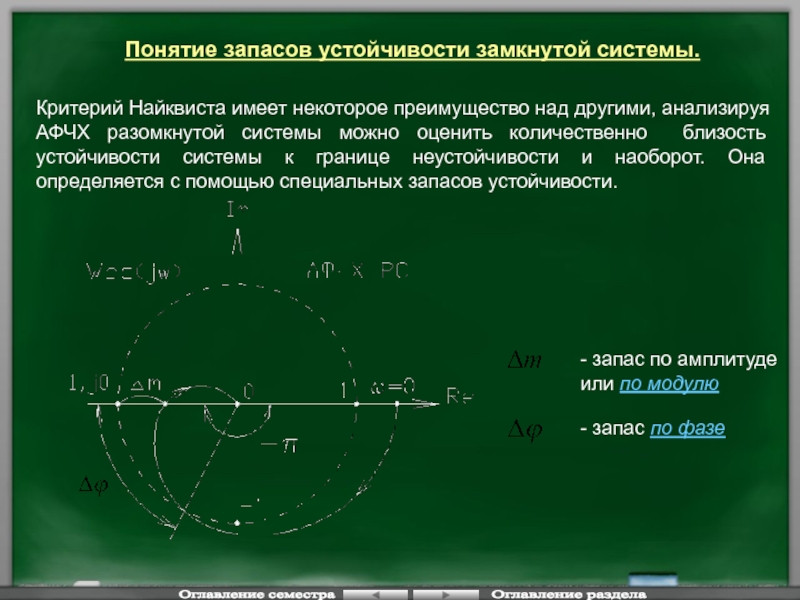
Слайд 88Понятие запасов устойчивости замкнутой системы.
Критерий Найквиста имеет некоторое преимущество над другими,
- запас по фазе
- запас по амплитуде
или по модулю
Оглавление семестра
Оглавление раздела
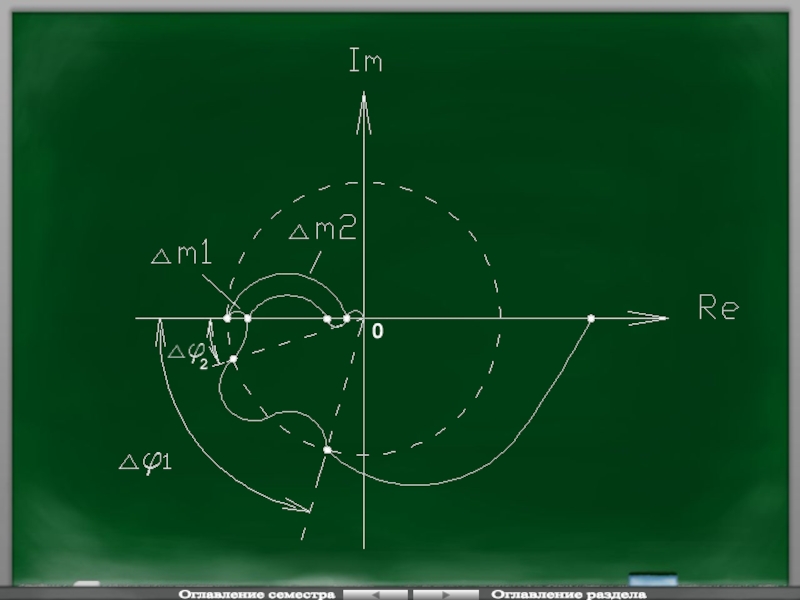
Слайд 90Трактовка критерия Найквиста с использованием ЛЧХ.
Применение рассмотренных ранее аналитической и графической
Формулировка: Для устойчивости замкнутой системы необходимо и достаточно, чтобы ЛАЧХ разомкнутой системы пересекала раньше ось 0, чем ЛФЧХ ось
- запас по амплитуде (по модулю) (в дб.)
- запас по фазе, в град. (рад.)
Оглавление семестра
Оглавление раздела
Замечание: Замкнутая система будет однозначно устойчивой, если ЛАЧХ целиком лежит ниже оси 0, а фазовая имеет всплеск над осью
Слайд 91В инженерной практике, в процессе проектирования реальных систем управления были выработаны
Связь между качеством системы и значением запасов – не жесткая, но величина запасов зависит от порядка разомкнутой системы и степени ее астатизма. Чем больше порядок астатизма и размерность разомкнутой системы, тем выше запас устойчивости.
Статические системы управления
Оглавление семестра
Оглавление раздела
Определение запасов устойчивости системы с использованием ЛЧХ.
Слайд 92Астатические первого порядка
Астатические второго порядка
Оглавление семестра
Оглавление раздела
Слайд 93Синтез систем автоматического управления методом типовых регуляторов.
Существует 5 типовых регуляторов. Среди
1) П – пропорциональный регулятор, W(p)=k (является простым, т.к. один параметр настройки - k). Является статическим регулятором.
2) И – интегрирующий регулятор
Так же является простым, но в отличие от первого он является астатическим.
3) ПИ – пропорционально-интегральный регулятор
Является сложным и астатическим.
4) ПД – пропорционально-дифференциальный регулятор
- является сложным и статическим.
5) ПИД – пропорционально-интегрально дифференцируемый регулятор
- является сложным и астатическим
Оглавление семестра
Оглавление раздела
Слайд 941) П – пропорциональный регулятор
Достоинства: Простота регулятора
Недостатки: Если объект статический, то
Является достаточно эффективным для астатических объектов.
Оглавление семестра
Оглавление раздела
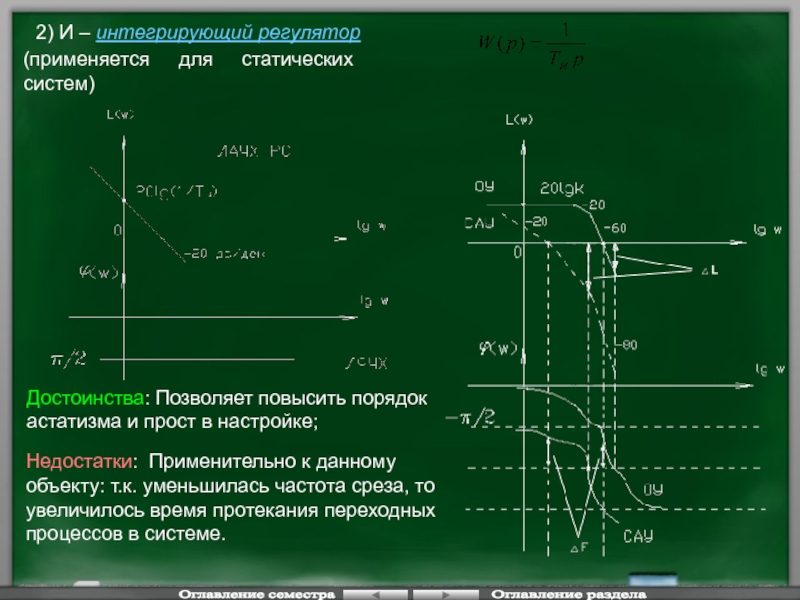
Слайд 952) И – интегрирующий регулятор
(применяется для статических систем)
Достоинства: Позволяет повысить порядок
Недостатки: Применительно к данному объекту: т.к. уменьшилась частота среза, то увеличилось время протекания переходных процессов в системе.
Оглавление семестра
Оглавление раздела
Слайд 963) ПИ – пропорционально-интегральный регулятор
Достоинства: Позволяет повысить порядок астатизма,
Применяется для статических систем и является самым распространенным в инженерной практике.
.
Недостатки: Cложность настройки, т.к. имеет два параметра
Оглавление семестра
Оглавление раздела
Слайд 974) ПД – пропорционально-дифференциальный регулятор
Достоинства: Расширяет возможности по обеспечению инженерных запасов
Недостатки: - Не повышает порядок астатизма и имеет 2 параметра настройки.
Применяется обычно для астатических объектов.
Оглавление семестра
Оглавление раздела
Слайд 985) ПИД – пропорционально-интегрально дифференцируемый регулятор
Оглавление семестра
Оглавление раздела
Слайд 99Построение областей устойчивости САУ
в плоскости их параметров.
Для построения
Исходными данными для построения областей – это характеристический полином замкнутой системы.
Оглавление семестра
Оглавление раздела
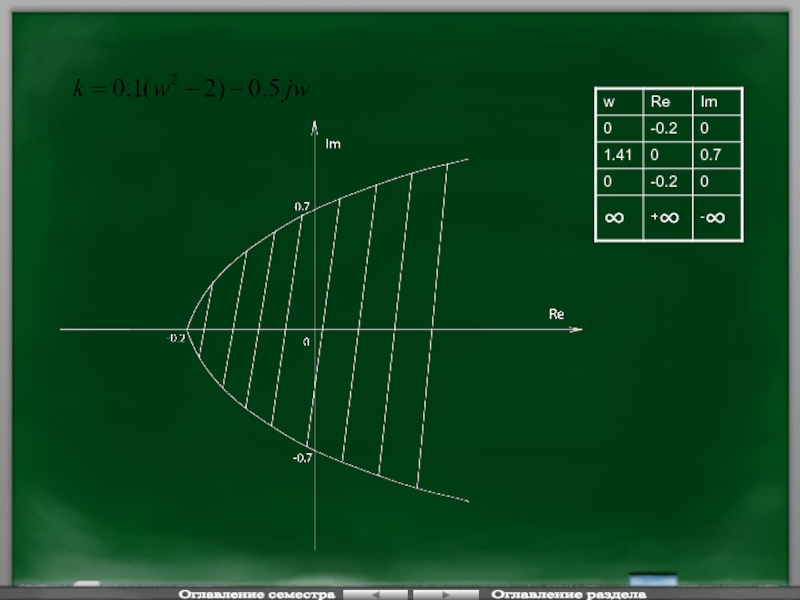
Слайд 100Однопараметрическое D-разбиение.
Исходными данными являются характеристический полином замкнутой системы,
Для определения области устойчивости САУ на параметрическую кривую необходимо нанести штриховку слева по мере увеличения частоты (по аналогии с корневой плоскостью).
Оглавление семестра
Оглавление раздела
Слайд 101Примечание: для построения параметрического годографа необязательно изменять частоту от
до
Достаточно
при этом оставшаяся часть будет зеркальным отражением построенного участка
вещественной оси. Так как варьируемый параметр является вещественным числом, то из полученной области устойчивости выделяется только отрезок вещественной оси, лежащей в области устойчивости.
Двухпараметрическое D-разбиение
Исходные данные: характеристический полином замкнутой системы, в который входят два варьируемых параметра.
от 0 до
Оглавление семестра
Оглавление раздела
Слайд 102
Так как M2 L2 и K2 являются нечетными функциями, то и
и
1)
также нечетные функции, а функции
Рассмотрим три возможных случая решения систем уравнений.
и
будут четными. При построении
параметрических кривых необходимо соблюдать следующее: по оси абсцисс
располагается параметр
, а по оси ординат -
Уравнения совместны и имеют общее решение
2)
Уравнения несовместны и не имеют общее решение
Оглавление семестра
Оглавление раздела
Слайд 1033)
- уравнение особой прямой
-
Особая прямая – линия, построенная
В большинстве практических случаев особые прямые получаются при
входит в коэффициенты,
и
В этом случае, хотя бы 1 из параметров -
или
соответствующие свободному числу
или
старшему числу характеристического полинома -
При
берется
а при
Если
и
независимы от
и
то особых прямых нет.
Правила штриховки параметрических кривых и особых прямых.
1. (Для параметрической кривой) При возрастании
от
до
граница
D-разбиения заштриховывается слева, если
, и справа, если
Так как
функции
и
четные, то при
и
кривые совпадают. Таким образом,
кривая D-разбиения обходится дважды и поэтому она всегда заштриховывается
двойной штриховкой.
Оглавление семестра
Оглавление раздела
Слайд 1042. (Для особых прямых) Штриховка особых прямых, как правило, одинарная и
и
кривой заштрихованные стороны кривой и прямой были направлены друг к другу.
После нанесения штриховки определяется область, претендующая на область устойчивость.
Области, претендующие на устойчивость – I и II. Область II после проверки будет действительно являться областью устойчивости.
При переходе через линию двойной штриховки их заштрихованной области в не заштрихованную два устойчивых корня становятся неустойчивыми.
При переходе через линию одинарной штриховки аналогично, неустойчивым становится один корень.
Оглавление семестра
Оглавление раздела
Слайд 107Оценка качества управления в линейных автоматических
системах.
Под качеством
К качественным показателям относят такие оценки как:
- быстродействие;
- колебательность;
- астатизм …
Для оценки качества систем управления используют понятие как критерий качества. Под ним понимается математическое выражение или система выражений, позволяющая вычислить количественную оценку качества управления по результатам исследований системы или ее математической модели.
Основные понятия и определения.
Оглавление семестра
Оглавление раздела
Слайд 108Методы оценки качества и виды
испытываемых воздействий для оценки.
В
- Прямая оценка качества (осуществляется по переходному процессу);
-Косвенная оценка качества (осуществляется по другим характеристикам, например, частотным или корневым).
Прямые методы исследования качества САУ.
Они состоят из 2-х основных этапов:
1) Построение переходного процесса;
2) Исследование переходного процесса и формирование показателей качества и критериев оценки.
Построение переходных процессов возможно 2-мя путями.
а) Экспериментальное исследование (в условиях эксплуатации)
б) Моделирование переходных процессов в системе (применяют при теоретическом исследовании и математическом моделировании).
Оглавление семестра
Оглавление раздела
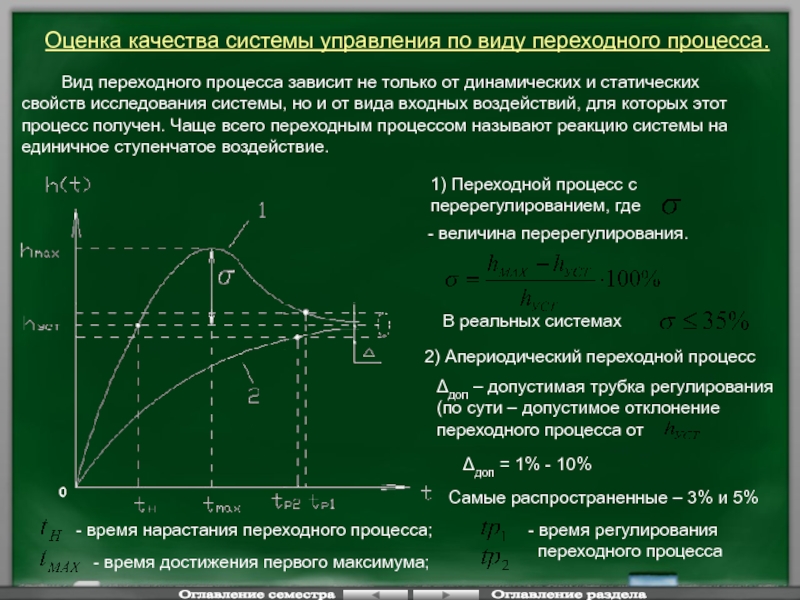
Слайд 109Оценка качества системы управления по виду переходного процесса.
1) Переходной процесс с
- величина перерегулирования.
В реальных системах
2) Апериодический переходной процесс
Δдоп – допустимая трубка регулирования (по сути – допустимое отклонение переходного процесса от
Δдоп = 1% - 10%
Самые распространенные – 3% и 5%
- время нарастания переходного процесса;
- время достижения первого максимума;
- время регулирования
переходного процесса
Вид переходного процесса зависит не только от динамических и статических свойств исследования системы, но и от вида входных воздействий, для которых этот процесс получен. Чаще всего переходным процессом называют реакцию системы на единичное ступенчатое воздействие.
Оглавление семестра
Оглавление раздела
Слайд 111Построение переходных процессов в САУ.
1) По изображению переходного процесса (по Лапласу);
2)
3) Прямым решением ДУ (описывающим динамику объектов этой системы).
1)
Для определения Y(p) важно знать изображение по Лапласу входного сигнала.
применяется в основном для типовых входных воздействий
(т.к . для них есть изображение по Лапласу).
2) Более универсальный способ по сравнению с предыдущим, т.к. применим для входных испытываемых воздействий любого сложного вида представимого в графической или аналитической формах.
Сущность подхода заключается в том, что реакция системы на входное воздействие произвольного вида может рассматриваться для линейных систем как суммарная реакция на Δ-функцию.
Оглавление семестра
Оглавление раздела
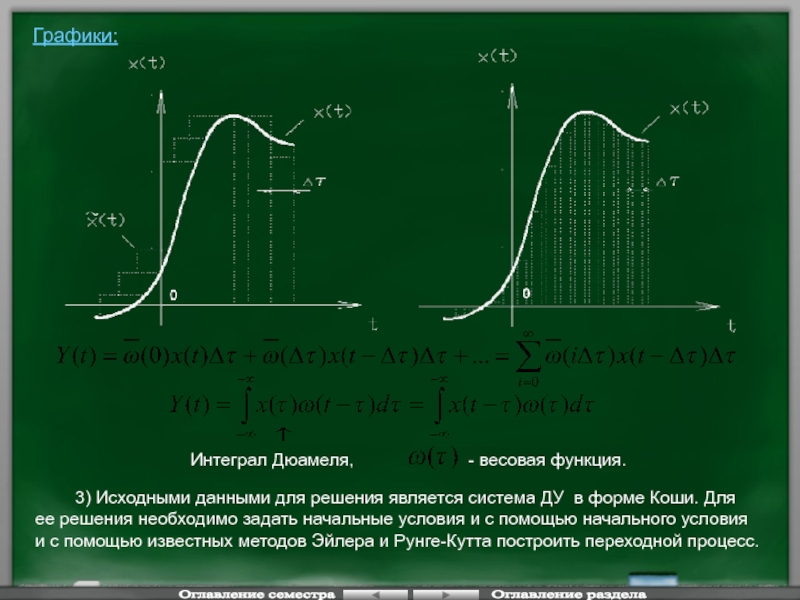
Слайд 112Графики:
Интеграл Дюамеля,
- весовая функция.
3) Исходными данными для решения является система
Оглавление семестра
Оглавление раздела
Слайд 113Аналитические методы анализа частных показателей
точности автоматических систем.
Анализ точности отработки типовых
Для анализа точности работы системы необходимо определить передаточную функцию по каналу ошибки.
Оглавление семестра
Оглавление раздела
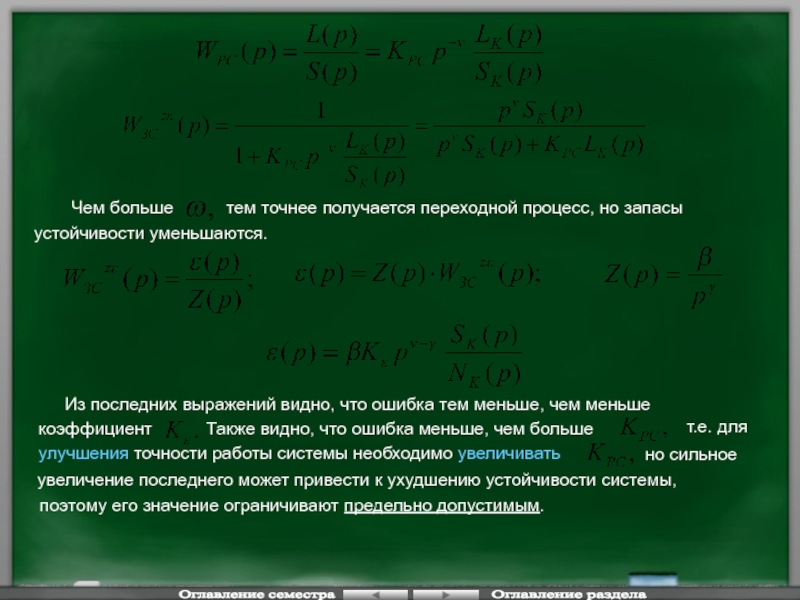
Слайд 114Чем больше
тем точнее получается переходной процесс, но запасы
устойчивости уменьшаются.
Из последних выражений видно, что ошибка тем меньше, чем меньше
коэффициент
Также видно, что ошибка меньше, чем больше
т.е. для
улучшения точности работы системы необходимо увеличивать
но сильное
увеличение последнего может привести к ухудшению устойчивости системы,
поэтому его значение ограничивают предельно допустимым.
Оглавление семестра
Оглавление раздела
Слайд 115Свойство преобразования Лапласа:
Используя выражения (1), (2) можно рассмотреть 3 случая соотношения
степеней
η:
1) γ > ν+1 (η<0)
Порядок степенной функции больше порядка астатизма, тогда ошибка отработки реакции данного сигнала неограниченно возрастает и система с
ним не справляется
ε(t)
2) γ = ν+1 (η=0)
Таким образом ошибка будет равна
ε(t)
Система как бы проявляет
статизм по отношению к данному сигналу.
3) γ < ν+1 (η>0)
ε(t)
0 .
При подаче такого сигнала на вход системы – ошибка отсутствует.
Оглавление семестра
Оглавление раздела
Совокупное значение
ν
γ
η.
и
дает некоторый показатель, называющийся
(1)
(2)
Слайд 1161) Если система является статической, то она отрабатывает единичное ступенчатое воздействие
2) Если система является астатической 1 порядка, то при ступенчатом воздействии ошибка равна нулю, при линейно-нарастающем - , а при параболическом стремится к бесконечности
3) При астатизме 2-го порядка, при ступенчатом и линейно-нарастающем,
ошибка равна нулю, а при параболическом -
Оглавление семестра
Оглавление раздела
Оценка ошибки в зависимости от порядка астатизма
линейно-нарастающее и
параболическое с ошибкой =
1) Если система является статической, то она отрабатывает единичное ступенчатое воздействие с ошибкой =
параболическое с ошибкой =
Слайд 117Для исследования реакции системы на различные виды воздействий можно
разложить в
при
дробную, рациональную
часть передаточной функции по каналу ошибкой.
1) Для обеспечения разложения функции определим частотные производные
по оператору p и находим их численные значения при p=0.
Исследование точности установившихся режимов воспроизведения методом коэффициентов ошибок.
Оглавление семестра
Оглавление раздела
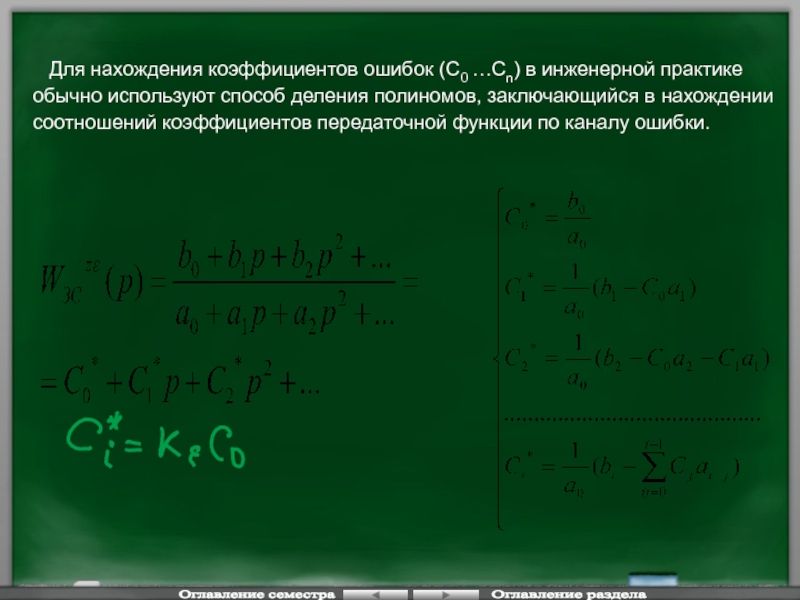
Слайд 118
Оглавление семестра
Оглавление раздела
Для нахождения коэффициентов ошибок (С0
Слайд 119Методы косвенной (приближенной) оценки качества линейных систем.
Частотные методы косвенной оценки.
Частотные методы
Если задано изображение Фурье входного сигнала, то переходной процесс связан с ним выражением для обратного преобразования Фурье.
Оглавление семестра
Оглавление раздела
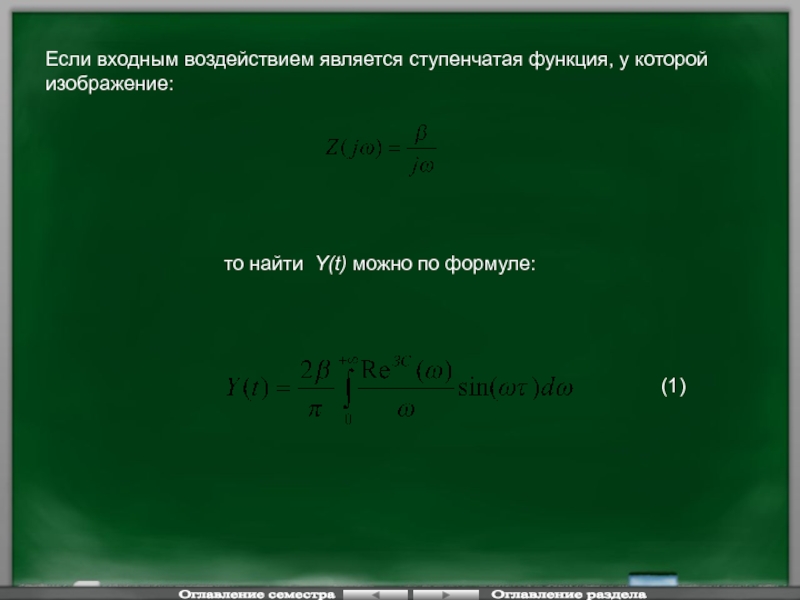
Слайд 120Если входным воздействием является ступенчатая функция, у которой изображение:
то найти
(1)
Оглавление семестра
Оглавление раздела
Слайд 121Качественная и приближенная количественная оценки переходных процессов в линейных системах по
Связь между переходным процессом и ВЧХ базируется на формуле (1) и характерным рядом фундаментальны свойств, позволяющих по внешнему виду ВЧХ и отдельным качественным характеристикам с достаточной для инженерной практики точностью оценивать вид и отдельные характеристики переходных процессов.
Свойства:
1) Линейность связи ВЧХ переходных процессов
- составляющая переходного процесса, полученная из
по формуле (1)
На этом свойстве базируется метод трапеций.
Оглавление семестра
Оглавление раздела
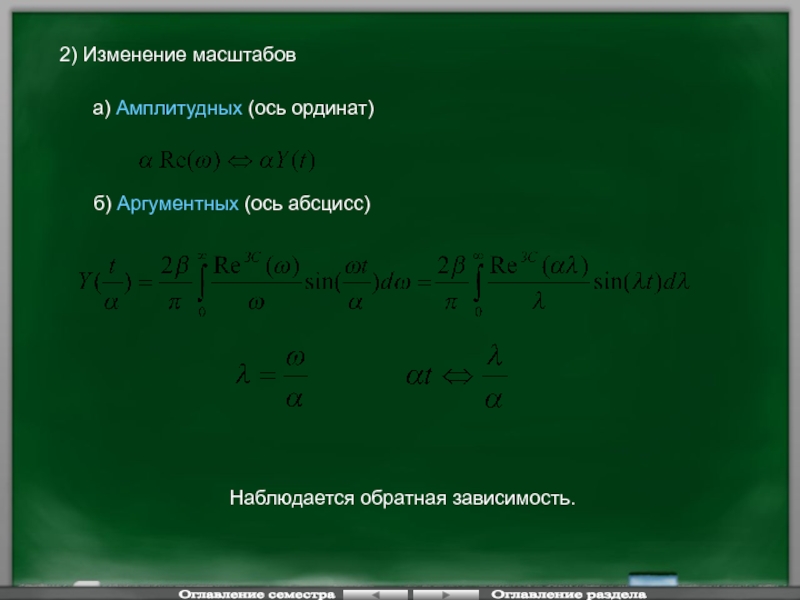
Слайд 122а) Амплитудных (ось ординат)
2) Изменение масштабов
б) Аргументных (ось абсцисс)
Наблюдается обратная зависимость.
Оглавление
Оглавление раздела
Слайд 1233) Обратность соответствия предельных значений, основано на предельной теореме
Оглавление семестра
Оглавление
Слайд 1244) Оценка экстремумов переходных процессов
а) Условие монотонности
Для монотонности Y(t)
Оглавление семестра
Оглавление раздела
Слайд 125б) Условия ограничения перерегулирования
Если ВЧХ является строго убывающей функцией, то перерегулирование
Оглавление семестра
Оглавление раздела
Слайд 126 в) Оценка наибольшего перерегулирования, при наличие у
Оглавление семестра
Оглавление раздела
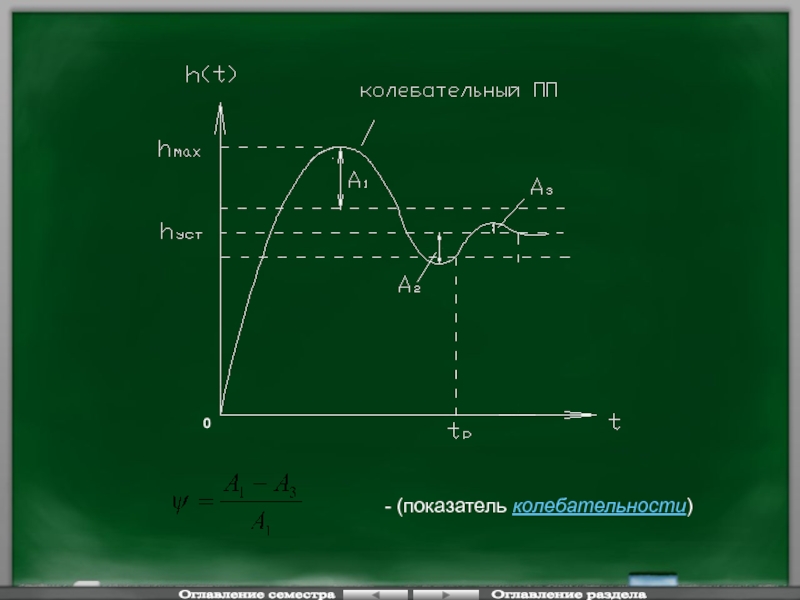
Слайд 1275) Оценка колебательности переходного процесса
При наличии данной формы ВЧХ в системе
Оглавление семестра
Оглавление раздела
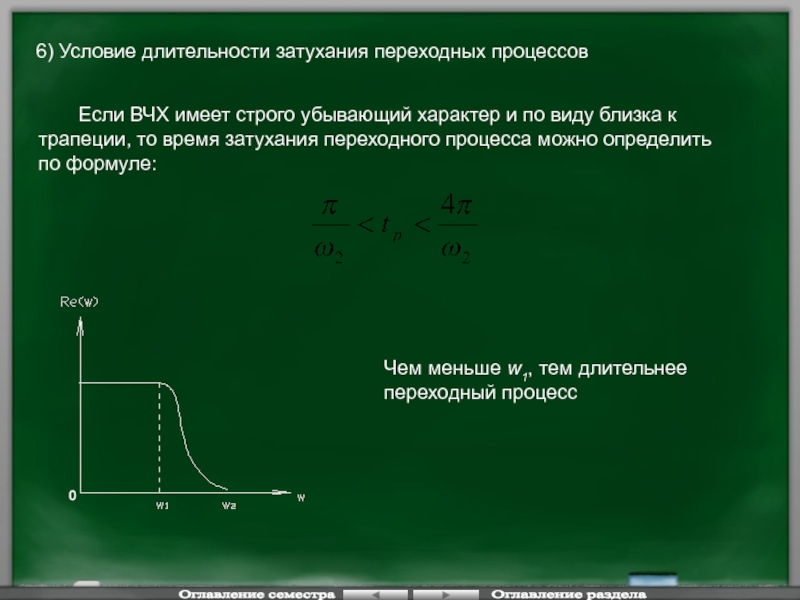
Слайд 1286) Условие длительности затухания переходных процессов
Если ВЧХ имеет строго убывающий характер
Чем меньше w1, тем длительнее переходный процесс
Оглавление семестра
Оглавление раздела
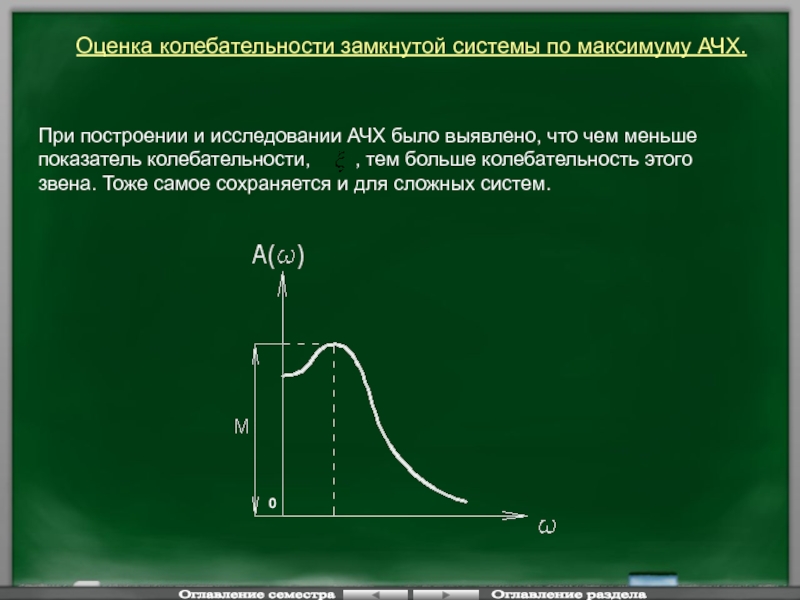
Слайд 129Оценка колебательности замкнутой системы по максимуму АЧХ.
При построении и исследовании АЧХ
Оглавление семестра
Оглавление раздела
Слайд 130Соответствие показателей колебательности.
M – максимум АЧХ
m – декремент затухания
– коэффициент колебательности
Оглавление семестра
Оглавление раздела
Слайд 131Оценка быстродействия замкнутой системы по частоте среза ЛАЧХ разомкнутой системы.
Коэффициент в
Оглавление семестра
Оглавление раздела
Слайд 132Корневые методы косвенной оценки качества системы управления.
Эти методы основаны на связи
Оценка быстродействия.
(для оценки используются корни характеристического полинома)
η – обозначает степень устойчивости
=0.03-0.05
Быстродействие системы определяется вещественной частью ближайшего к мнимой оси корней.
Оглавление семестра
Оглавление раздела
Слайд 133Оценка колебательности.
(является более удобным)
Эти формулы справедливы полностью для объектов второго
Оглавление семестра
Оглавление раздела
Слайд 134Совокупная оценка качества.
х1,2 удовлетворяют ограничению
х3 не удовлетворяет быстродействию, но удовлетворяет колебательности
х4
Оглавление семестра
Оглавление раздела