- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Тема: Расчет разветвленной магнитной цепи презентация
Содержание
- 1. Тема: Расчет разветвленной магнитной цепи
- 2. Расчет разветвленных магнитных цепей Расчеты разветвленных магнитных
- 3. Последовательность расчета симметричных магнитных цепей.
- 4. Последовательность расчета несимметричных магнитных цепей.
- 5. Основные соотношения. Когда в разветвленной магнитной цепи
- 6. Расчёты При I1 > 0 и I2 = 0
- 7. Рассмотрим соотношения между напряженностями, магнитными индукциями и
- 8. Разветвленная магнитная цепь Пусть заданы кривая
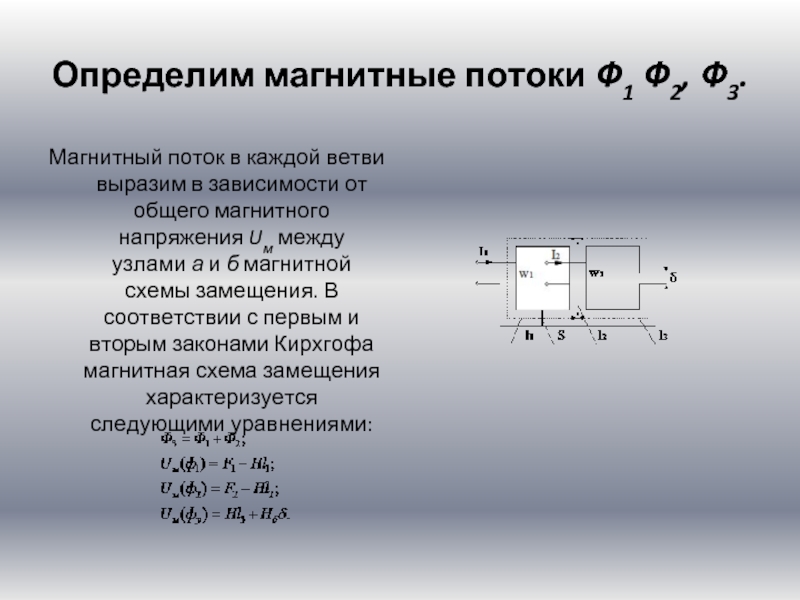
- 9. Определим магнитные потоки Ф1 Ф2, Ф3. Магнитный поток в
- 10. Эти уравнения решаются графически. Для этого: ·
- 11. Примечание. В воздушных зазорах магнитных цепей различных
Слайд 1
Тема : Расчет разветвленной магнитной цепи
Подготовил:
Студент группы ОМД-13
Данилов В.С
Проверила :
Чернуха
Слайд 2Расчет разветвленных магнитных цепей
Расчеты разветвленных магнитных цепей основаны на применении законов
Слайд 3 Последовательность расчета симметричных магнитных цепей.
Предположим, что имеется разветвленная симметричная магнитная цепь
В силу симметрии магнитной цепи и выражения можно утверждать, что
Ф1 = Ф2 = Ф/2.
Вследствие простого соотношения между магнитными потоками расчет разветвленных симметричных магнитных цепей производится практически в том же порядке, что и расчет неразветвленных магнитных цепей.
Обычно при расчете симметричную магнитную цепь делят мысленно на две одинаковые части по оси симметрии ab и производят расчет одной ее половины.
Слайд 4Последовательность расчета несимметричных магнитных цепей.
Расчет несимметричных магнитных цепей производится графоаналитическим методом
Рассмотрим в качестве примера последовательность расчета магнитной цепи, если требуется определить МДС I1w1 при заданной магнитной индукции Вδ2 и известной МДС I2w2.
Зная Вδ2, нетрудно найти магнитный поток Ф2 = Вδ2Sδ2, а затем подсчитать магнитное напряжение Umab :
Umab = I2w2 - H2l2 - Hδ2lδ2 - H5l5.
Построив с помощью уравнения Umab = Н3l3 вб. а. х. Ф3(Umab) и зная магнитное напряжениеUmab, легко определить магнитный поток Ф3.
Зная потоки Ф2 и Ф3, найдем поток Ф1 = Ф3 — Ф2. После этого можно определить МДС I1w1.
I1w1 = Н1l1 + Hδ1lδ1 + Н4l4 + Umab .
Слайд 5 Основные соотношения.
Когда в разветвленной магнитной цепи магнитные потоки возбуждаются одной обмоткой,
Рассмотрим в качестве примера возможные направления магнитных потоков в магнитной цепи изображенном на рисунке.
Слайд 6Расчёты
При I1 > 0 и I2 = 0 магнитные потоки Ф1 и Ф3 будут направлены так,
Изменяя I1 при I2 = const или I2 при I1 = const, можно получить Ф1 <> 0 и Ф2 <> 0; магнитный поток Ф3 при любых токах I1 > 0 и I2 > 0 будет направлен так, как показано на рисунке.
Так как в каждой ветви разветвленной магнитной цепи магнитный поток имеет одно и то же значение, между магнитными индукциями, а также между напряженностями участков любой ветви существуют соотношения, полученные ранее для неразветвленной цепи.
Слайд 7Рассмотрим соотношения между напряженностями, магнитными индукциями и потоками двух ветвей amb и аnb,не содержащих
По закону полного тока для контуров аmbа и аnbа имеем
H1l1 - Umab = 0 и H2l2 - Umab = 0.
Из полученных уравнений следует, что
(6.15)
H1 /H2 = l2 /l1.
Если l1 = l2, то независимо oт площадей поперечного сечения S1 и S2, а также марки ферромагнитных материалов ветвей получим Н1 = Н2. Если ветви выполнены из одинакового ферромагнитного материала, то при H1 = Н2 и
В1 = В2. Магнитные потоки ветвей в случае В1 = В2 будут равны лишь при равенстве площадей, так как Ф1 = В1S1, a
Ф2 = B2S2.
Если в магнитной цепи l1 > l2, то согласно (6.15) H1 < H2 и, следовательно, В1 < В2. Количественное соотношение между потоками зависит от соотношений между индукциями и площадями :
Ф1=В1S1;Ф2В2S2Может оказаться, например, что Ф1 > Ф2 при В1 < В2 .
На соотношение напряженностей, магнитных индукций и потоков существенное влияние оказывают воздушные зазоры. Допустим, что во вторую ветвь введен воздушный зазор длиной lδ. Тогда
(6.16)
H1l1 = H2l2 + (Hδ - H2)lδ.
Так как обычно Hδ >> H2, вместо (6.16) можно написать
H1l1 = H2l2 + Hδlδ,
откуда следует, что при l1 = l2 H1 > H2; как правило, Hδlδ в несколько раз превышает H2l2, поэтому напряженность H2 в ветви с воздушным зазором в несколько раз меньше напряженности H1.
Слайд 8Разветвленная магнитная цепь
Пусть заданы кривая намагничивания В(Н) ферроманитного материала сердечника и геометрические размеры
Слайд 9Определим магнитные потоки Ф1 Ф2, Ф3.
Магнитный поток в каждой ветви выразим в зависимости
Слайд 10Эти уравнения решаются графически.
Для этого:
· произвольно задают значение магнитной индукции В и соответствующую
· по известной В определяют магнитные потоки Ф1 Ф2, Ф3,;
· по приведенным выше уравнениям рассчитывают магнитные напряжения Uм1, Uм2 , Uм3 ;
·производят аналогичный расчет для нескольких точек и строят зависимости Uм(Ф1), Uм(Ф2), Uм(Ф3);
· с учетом того, что Ф3 = Ф1 + Ф2, графически складывают характеристики Uм(Ф1) и Uм(Ф2)(суммируя ординаты кривых при одних и тех же значениях магнитного напряжения);
· точка пересечения суммарной кривой Uм(Ф1 + Ф2) с кривой Uм(Ф3) определяет поток Ф3 ;
· чтобы найти потоки Ф1, Ф2 через найденную точку пересечения проводят прямую, параллельную оси магнитного напряжения Uм, до пересечения с кривыми Uм(Ф1) и Uм(Ф2).
Слайд 11Примечание.
В воздушных зазорах магнитных цепей различных устройств действует механическая сила, которая
где Ф и В магнитный поток и индукция в воздушном зазоре.