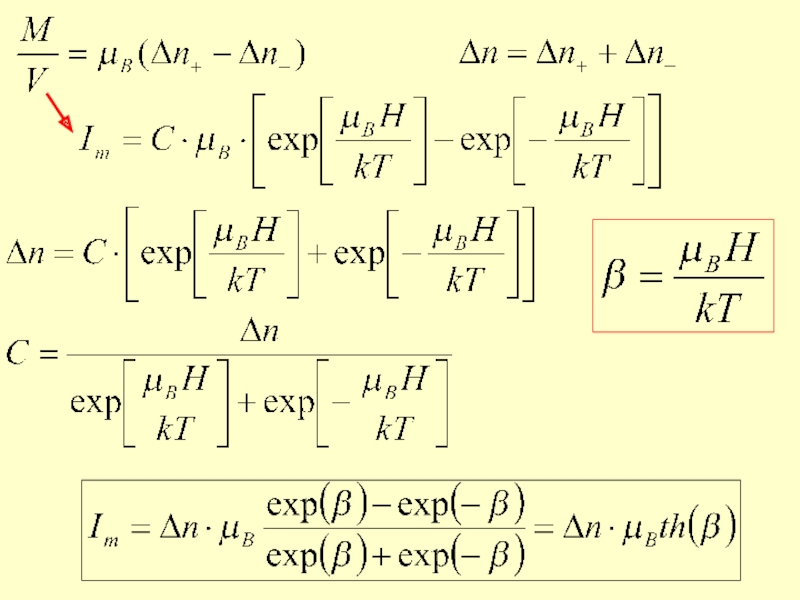- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Тема 6. Магнитные возбуждения в твердом теле. Магнетизм презентация
Содержание
- 1. Тема 6. Магнитные возбуждения в твердом теле. Магнетизм
- 3. Магнетизм атомов Магнитный
- 4. Одноэлектронные атомы
- 5. Одноэлектронные атомы
- 6. Одноэлектронные атомы Спин-орбитальное взаимодействие Поправки к энергии – тонкая структура уровней
- 7. Магнетизм многоэлектронных атомов Многоэлектронный атом можно рассматривать
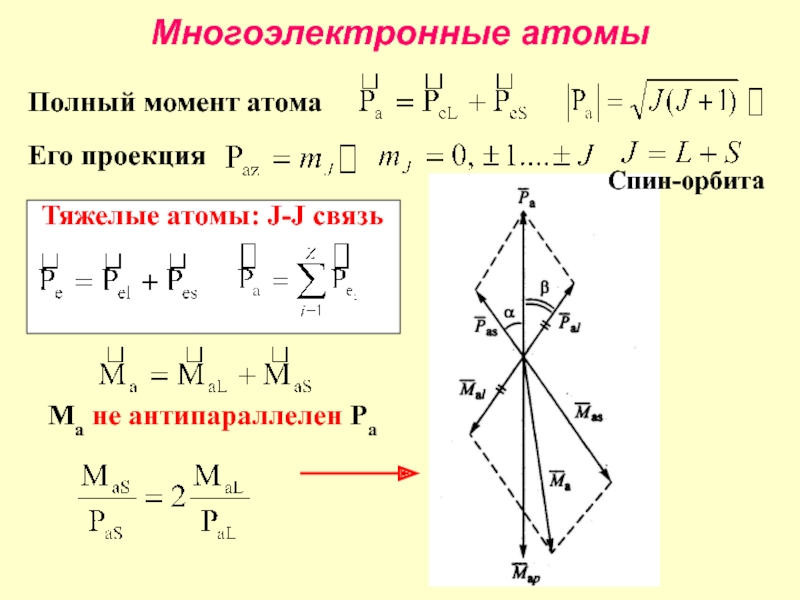
- 8. Многоэлектронные атомы Полный орбитальный момент атома
- 9. Многоэлектронные атомы Ma не антипараллелен Pa
- 10. Проекция магнитного момента, на направление механического момента Из геометрических соображений:
- 11. Многоэлектронные атомы
- 12. Магнитные моменты атомных ядер Аналогия протона с электроном не проходит !!!
- 13. Основы теории магнетизма т.т. Все тв.тела. в
- 14. По магнитным свойствам все вещества делятся на:
- 15. Основы теории магнетизма
- 16. Диамагнетизм – κ
- 17. В атоме содержащем Z электронов суммарный
- 18. Парамагнетизм κ >0 не зависит H, зависит
- 20. Парамагнетики Для N атомов намагниченность Im равна N·MH Для β
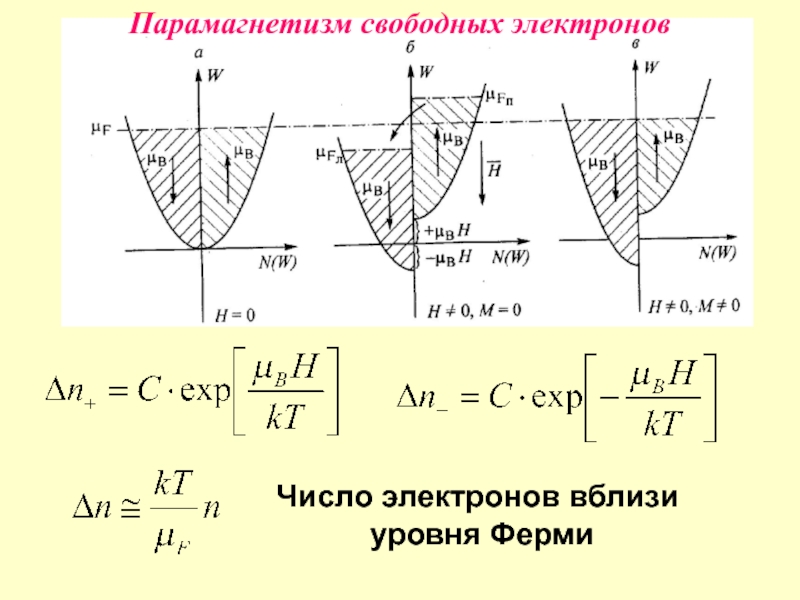
- 21. Парамагнетизм свободных электронов
- 23. Магнитная восприимчивость e не зависит от Т
- 24. Ферромагнетики κ >>0 и зависит от H
- 25. Тождественность частиц в.ф. системы, получающиеся при перестановке
- 26. Принцип Паули В.ф. Системы двух невзаимодействующих электронов
- 27. Обменное взаимодействие
- 28. Обменное взаимодействие Вероятность нахождения частиц в одной и той же точке пространства
- 29. Обменное взаимодействие W= - 2I(S1,S2)
- 31. Ферримагнетики Неравенство магнитных моментов атомов в различных подрешетках парамагнетик ферромагнетик антиферромагнетик ферримагнетик
- 32. Доменая структура
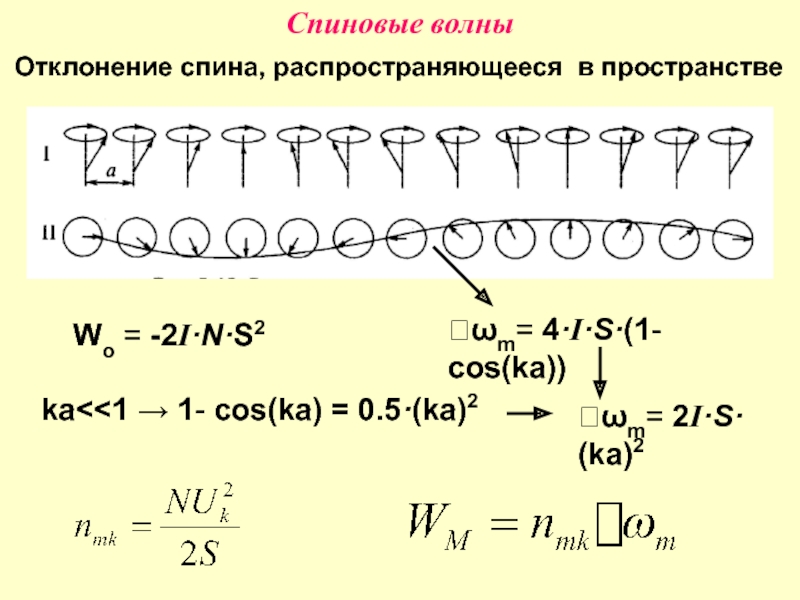
- 33. Спиновые волны Отклонение спина, распространяющееся в пространстве Wo = -2I·N·S2 ka
Слайд 2
Источник магнитного поля - движение зарядов
Магнетизм – взаимодействие между
движущимися зарядами
Взаимодействие осуществляется магнитным полем
Количественная характеристика магнитного поля –
его напряженность H
Слайд 3Магнетизм атомов
Магнитный момент атома обусловлен
микроскопическими токами,
1) орбитальным движением электронов
2) спинами электронов и ядер
Способность атомов взаимодействовать с магнитным полем характеризуется магнитным моментом M
Слайд 6Одноэлектронные атомы
Спин-орбитальное взаимодействие
Поправки к энергии – тонкая структура уровней
Слайд 7Магнетизм многоэлектронных атомов
Многоэлектронный атом можно рассматривать в приближении
самосогласованного центрально-симметричного электрического
Квантовое состояние определяется электронной конфигурацией т.е. числом электронов с заданными l и n
Мах число таких состояний 2(2 l +1)
например 1p → 6 эквивалентных сост.
Все состояния c данным n –составляют электронную оболочку. Замкнутая оболочка – электронный слой
Заполнение оболочек e
K 1s2 2 электрона
L 2s2, 2p6 8 электронов
M 3s2, 3p6, 3d10 18 электронов
N 4s2, 4p6 4d10, 4f14 32 электрона
Уровни энергии в сложный атомах обозначают
большими буквами латинского алфавита
Слайд 10Проекция магнитного момента, на
направление механического момента
Из геометрических соображений:
Слайд 13Основы теории магнетизма т.т.
Все тв.тела. в магнитом поле H – приобретают
Вектор намагниченности Im - магнитный момент ед. объема
Слайд 14По магнитным свойствам все вещества делятся на:
феноменология
Диамагнетики κ
Парамагнетики κ >0 не зависит H, зависит от T ( μ > 1)
Ферромагнетики κ >>0 и зависит от H :
ферромагнетики,
антиферромагнетики
ферримагнетики
Причины – Изменение магнитного момента атомов
во внешнем магнитном поле,
Взаимодействие магнитных моментов атомов
Слайд 16Диамагнетизм – κ
Теорема Лармора – влияние H на движение
электрона в атоме – прецессия вокруг направления Н
с частотой Ω = eH/2m
Прецессия электронной орбиты
эквивалентна току I = - ev = - e Ω/ 2π
Связанный с током магнитный момент M = I·S
Слайд 17В атоме содержащем Z электронов суммарный ток I = (- eZ)
Диамагнетизм есть всегда, но проявляется в атомах с нулевым собственным
магнитным моментом
Слайд 18Парамагнетизм κ >0 не зависит H, зависит от T ( μ
Имеет место в т.т. состоящих из атомов с
ненулевым собственным магнитным моментом
В отсутствие внешнего H моменты атомов
распределены случайно и В магнитном поле моменты стремятся
ориентироваться по полю Энергия момента, отклоненного от поля на угол Θ : Тепловое движение наоборот, разупорядочивает моменты Надо найти среднее значение < MaH>
под действием поля и температуры
Слайд 20Парамагнетики
Для N атомов намагниченность Im равна N·MH
Для β
Закон Кюри - Вейса κ =С/(T- Θ)
Слайд 24Ферромагнетики
κ >>0 и зависит от H
Домены - области спонтанной намагниченности
параллельная ориентация
Источники образования доменов:
Не скомпенсированный спин электронных оболочек
Обменное взаимодействие электронов
Электростатическая природа!!!!
Слайд 25Тождественность частиц
в.ф. системы, получающиеся при перестановке пары одинаковых частиц отличаются множителем
Для систем с S=n/2 В.Ф. Антисимметрична -
Меняет знак при при нечетном числе перестановок
Для систем с S=n В.Ф. Симметрична –
Не меняет знак при любом числе перестановок
Слайд 26Принцип Паули
В.ф. Системы двух невзаимодействующих электронов
ΨI(1,2) = Ψα(1)·Ψβ(2) ΨI I(1,2) =
Ψ = c1·Ψ I + c2·ΨI I в.ф. Антисимметрична т.е. c1=- c2
Ψанти(1,2) = [1/√2] ·[Ψα(1)·Ψβ(2)-Ψα(2)·Ψβ(1)]
Если электроны в одном состоянии то
Ψα = Ψβ ⇒ Ψанти(1,2)≡0