и релятивистской механики
6 лекций
(12 аудиторных часов)
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Тема 1,Кин-ка вращ., лекция 2, версия 3 презентация
Содержание
- 1. Тема 1,Кин-ка вращ., лекция 2, версия 3
- 2. Тема 2. Кинематика вращательного движения
- 3. 2.1. Угловое перемещение. Угловая скорость. Любое
- 4. При вращательном движении все точки тела движутся
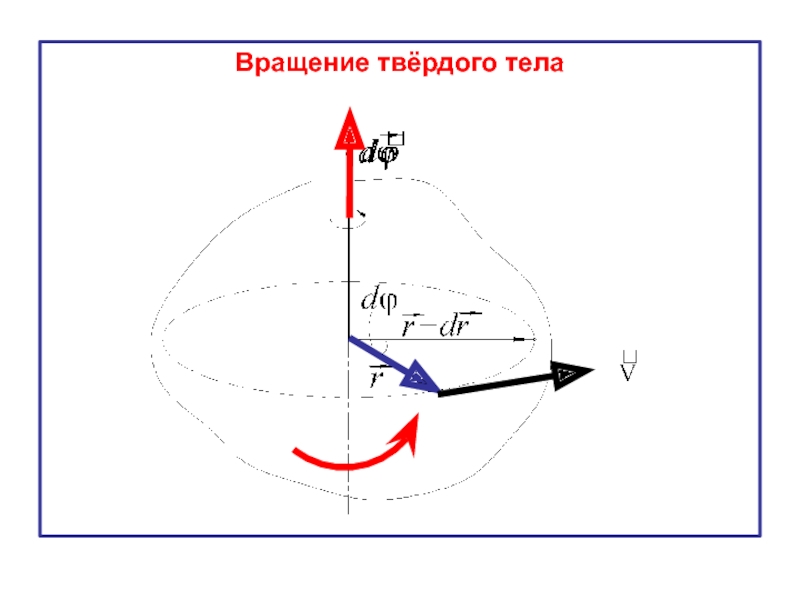
- 5. Вращение твёрдого тела
- 6. Угловое перемещение
- 7. Угловая скорость характеризует быстроту изменения углового
- 8. Мгновенная угловая скорость равна пределу, к которому
- 9. Направление углового перемещения и угловой скорости
- 10. характеризует быстроту изменения угловой скорости с течением
- 11. Мгновенное угловое ускорение равно пределу, к которому
- 12. Модуль мгновенного углового ускорения равен первой производной
- 13. Направления угловых векторов
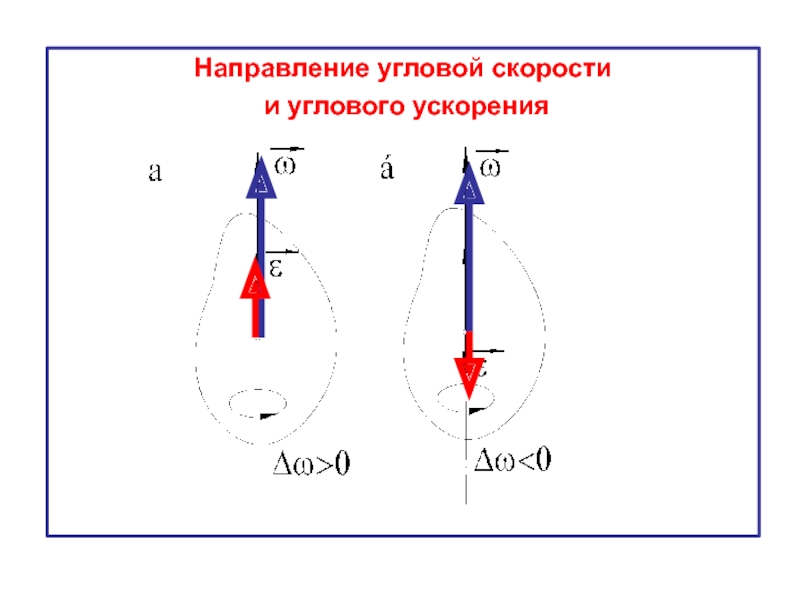
- 14. Направление угловой скорости и углового ускорения
- 15. 2.3. Обратная задача кинематики при вращательном
- 16. При равномерном вращении ε = 0,
- 17. Период и частота вращения Для характеристики равномерного
- 18. 1.4. Взаимосвязь угловых и линейных величин Кроме
- 19. Пусть за время dt произвольная точка твёрдого
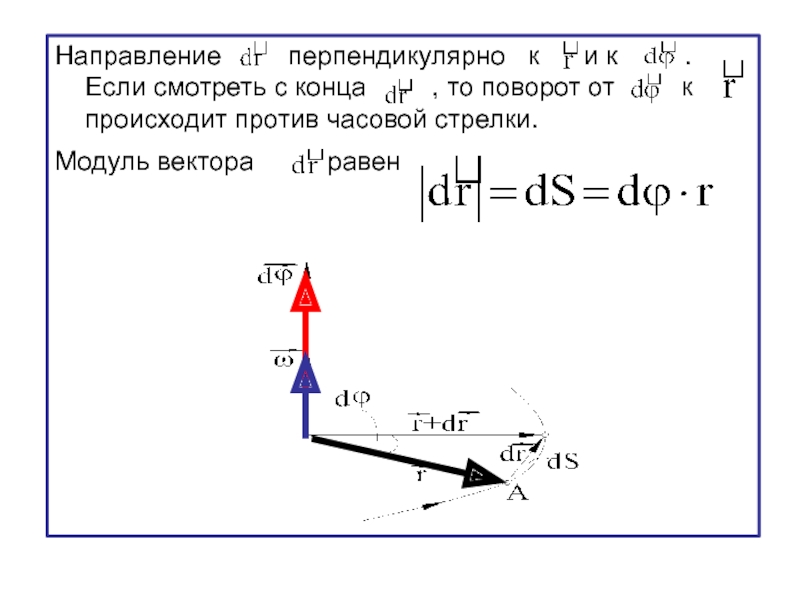
- 20. Направление перпендикулярно
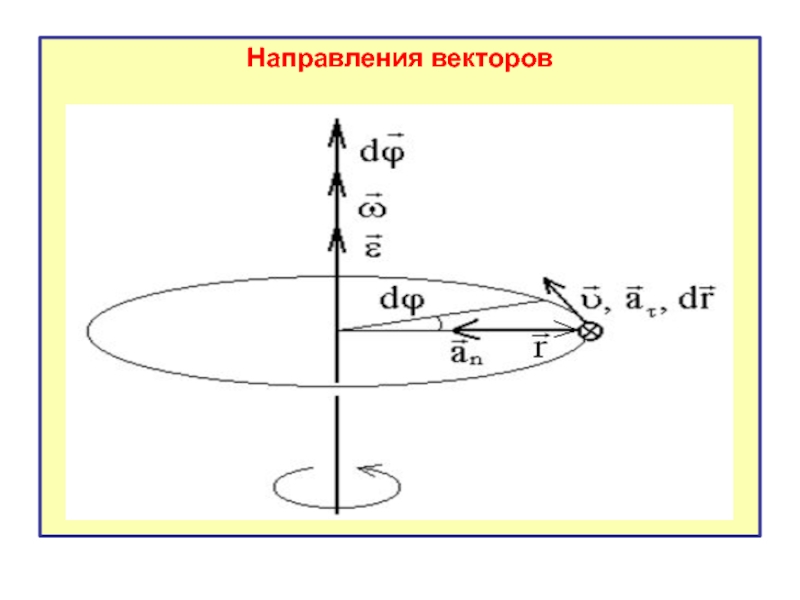
- 21. Направления векторов
- 22. Вектор элементарного перемещения: Разделим это
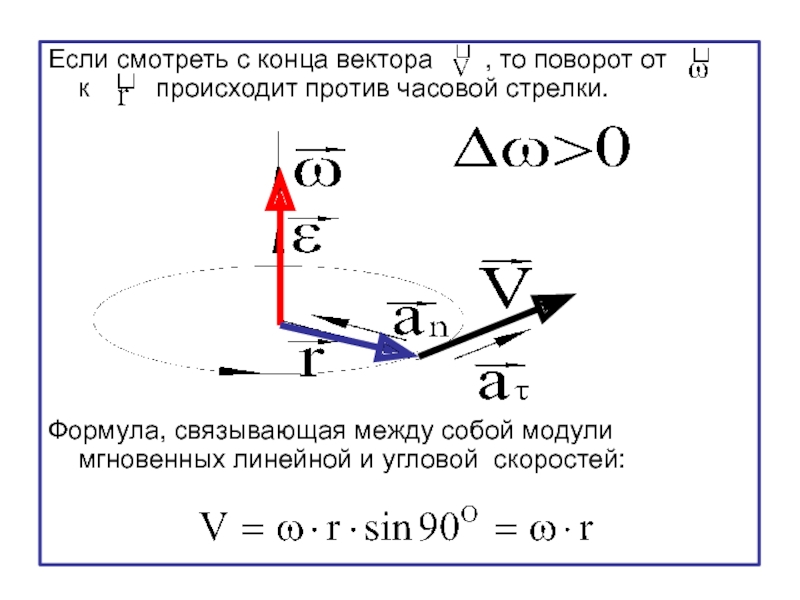
- 23. Если смотреть с конца вектора
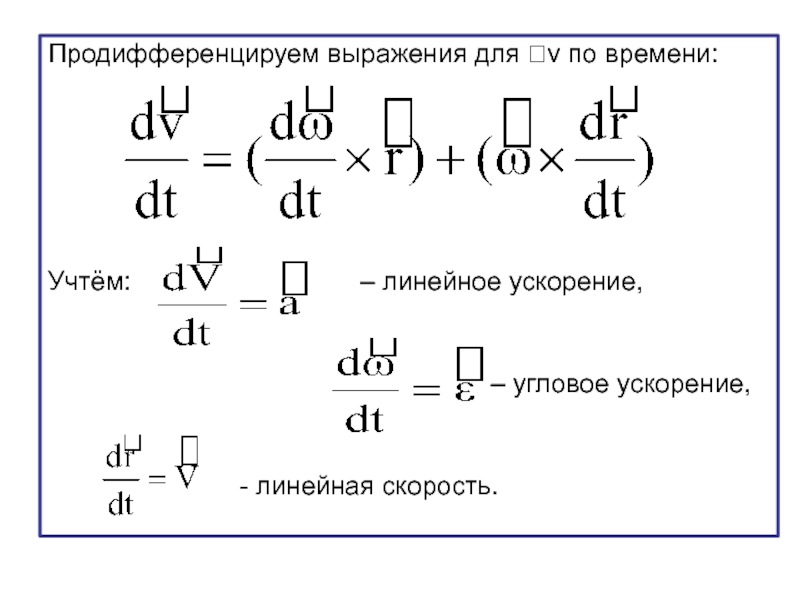
- 24. Продифференцируем выражения для v по времени:
- 25. Получим и сравним
- 26. Тангенциальное ускорение характеризует изменение модуля линейной скорости.
- 27. Нормальное ускорение характеризует изменение направления линейной
Тема 2.
Кинематика вращательного движения Тема лекции 2.1. Угловое перемещение. Угловая скорость. 2.2. Угловое ускорение. 2.3. Обратная задача кинематики при вращательном движении. 2.4. Взаимосвязь линейных
Слайд 1Омский государственный технический университет
Кафедра физики
Калистратова Л.Ф.
Электронные лекции по разделам классической
Слайд 2Тема 2.
Кинематика вращательного движения
Тема лекции
2.1. Угловое перемещение. Угловая скорость.
2.2.
Угловое ускорение.
2.3. Обратная задача кинематики при вращательном движении.
2.4. Взаимосвязь линейных и угловых величин.
2.3. Обратная задача кинематики при вращательном движении.
2.4. Взаимосвязь линейных и угловых величин.
Слайд 32.1. Угловое перемещение.
Угловая скорость.
Любое движение абсолютно твёрдого тела может быть
сведено к сумме двух движений – поступательного и вращательного.
При вращательном движении различные точки твёрдого тела движутся по-разному.
Вращательное движение нельзя охарактеризовать движением определённой точки.
При вращательном движении различные точки твёрдого тела движутся по-разному.
Вращательное движение нельзя охарактеризовать движением определённой точки.
Слайд 4При вращательном движении все точки тела движутся по окружностям, центры которых
лежат на одной неподвижной прямой, называемой осью вращения.
При вращательном движении радиус-векторы, проведённые из центров соответствующих окружностей к точкам тела за время dt поворачиваются на один и тот же угол dϕ.
При вращательном движении радиус-векторы, проведённые из центров соответствующих окружностей к точкам тела за время dt поворачиваются на один и тот же угол dϕ.
Слайд 6Угловое перемещение – вектор, численно
равный углу поворота dϕ радиус-вектора определённой точки вращающегося тела.
измеряется в радианах: [φ] = рад.
Его направление определяется правилом буравчика:
Вектор dϕ направлен вдоль оси вращения так, что если смотреть с его конца, то вращение тела должно происходить против часовой стрелки.
измеряется в радианах: [φ] = рад.
Его направление определяется правилом буравчика:
Вектор dϕ направлен вдоль оси вращения так, что если смотреть с его конца, то вращение тела должно происходить против часовой стрелки.
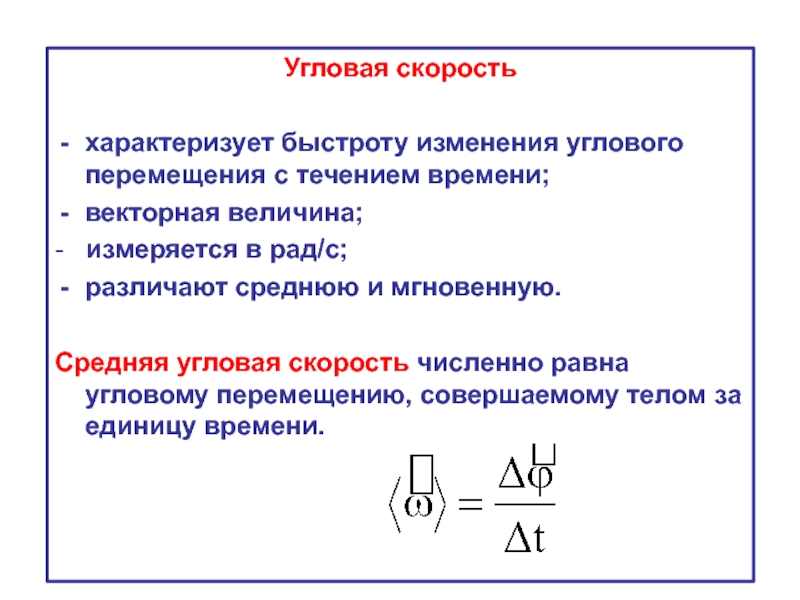
Слайд 7Угловая скорость
характеризует быстроту изменения углового перемещения с течением времени;
векторная величина;
-
измеряется в рад/с;
различают среднюю и мгновенную.
Средняя угловая скорость численно равна угловому перемещению, совершаемому телом за единицу времени.
различают среднюю и мгновенную.
Средняя угловая скорость численно равна угловому перемещению, совершаемому телом за единицу времени.
Слайд 8Мгновенная угловая скорость равна пределу, к которому стремится средняя угловая скорость
при неограниченном убывании промежутка времени до нуля.
Мгновенная угловая скорость равна первой производной от углового перемещения по времени.
Вектор угловой скорости направлен по оси вращения и определяется по правилу буравчика.
Мгновенная угловая скорость равна первой производной от углового перемещения по времени.
Вектор угловой скорости направлен по оси вращения и определяется по правилу буравчика.
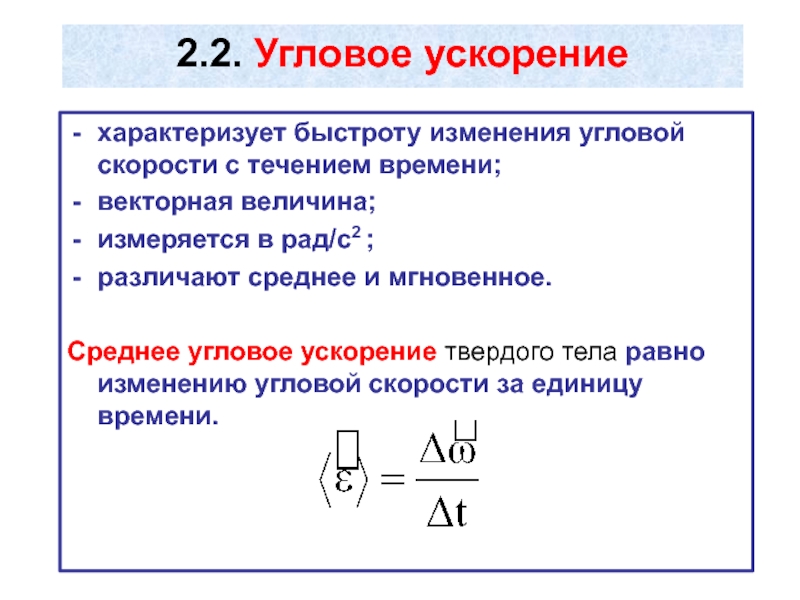
Слайд 10характеризует быстроту изменения угловой скорости с течением времени;
векторная величина;
измеряется в рад/с2
;
различают среднее и мгновенное.
Среднее угловое ускорение твердого тела равно изменению угловой скорости за единицу времени.
различают среднее и мгновенное.
Среднее угловое ускорение твердого тела равно изменению угловой скорости за единицу времени.
2.2. Угловое ускорение
Слайд 11Мгновенное угловое ускорение равно пределу, к которому стремится среднее угловое ускорение
при неограниченном убывании промежутка времени до нуля.
Мгновенное угловое ускорение равно первой производной от угловой скорости по времени.
Мгновенное угловое ускорение равно первой производной от угловой скорости по времени.
Слайд 12Модуль мгновенного углового ускорения равен первой производной от модудя угловой скорости
по времени или второй производной от углового перемещения по времени.
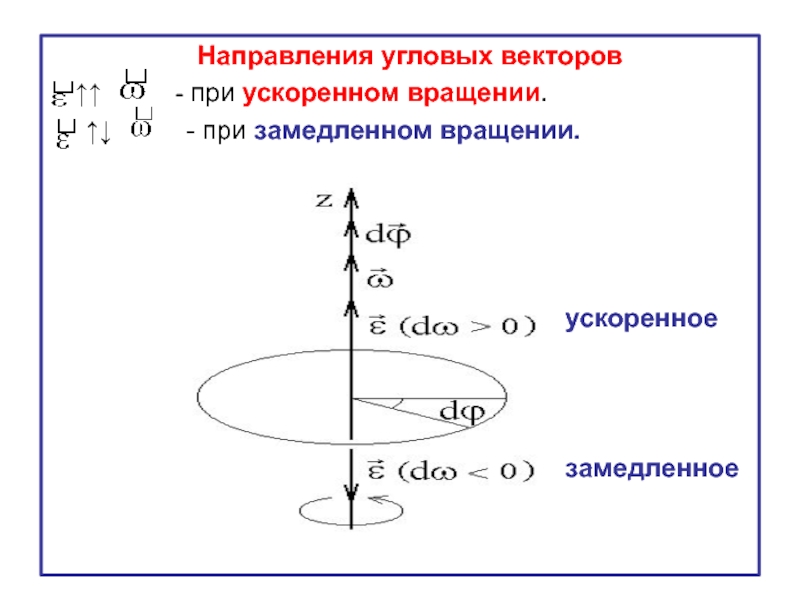
Слайд 13 Направления угловых векторов
↑↑
- при ускоренном вращении.
↑↓ - при замедленном вращении.
ускоренное
замедленное
↑↓ - при замедленном вращении.
ускоренное
замедленное
Слайд 152.3. Обратная задача кинематики
при вращательном движении
При вращательном движении обратная задача
кинематики выполняется при следующих формулах:
Слайд 17Период и частота вращения
Для характеристики равномерного вращательного движения используются следующие величины.
Период
вращения Т – время одного оборота тела, вращающегося с постоянной угловой скоростью.
Частота вращения ν – количество оборотов, совершаемых телом за единицу времени.
Угловая скорость связана с периодом следующим образом:
Частота вращения ν – количество оборотов, совершаемых телом за единицу времени.
Угловая скорость связана с периодом следующим образом:
Слайд 181.4. Взаимосвязь угловых и линейных величин
Кроме угловых величин: углового перемещения, угловой
скорости и углового ускорения движение каждой точки вращающегося твердого тела характеризуют линейные величины:
линейное перемещение ,
линейный путь dS,
линейная скорость ,
тангенциальное ускорение ,
нормальное ускорение ,
полное ускорение .
линейное перемещение ,
линейный путь dS,
линейная скорость ,
тангенциальное ускорение ,
нормальное ускорение ,
полное ускорение .
Слайд 19Пусть за время dt произвольная точка твёрдого тела переместится на
, пройдя путь dS. При этом радиус - вектор точки повернется на угол .
Тогда
В векторном виде:
dS
Тогда
В векторном виде:
dS
Слайд 20Направление перпендикулярно к и
к . Если смотреть с конца , то поворот от к происходит против часовой стрелки.
Модуль вектора равен
Модуль вектора равен
Слайд 22Вектор элементарного перемещения:
Разделим это соотношение на dt:
Учтём, что
Получим
Линейная скорость данной
точки твёрдого тела равна векторному произведению угловой скорости на радиус - вектор точки.
.
Слайд 23Если смотреть с конца вектора , то поворот
от к происходит против часовой стрелки.
Формула, связывающая между собой модули мгновенных линейной и угловой скоростей:
Формула, связывающая между собой модули мгновенных линейной и угловой скоростей:
Слайд 24Продифференцируем выражения для v по времени:
Учтём:
– линейное ускорение,
– угловое ускорение,
- линейная скорость.
– угловое ускорение,
- линейная скорость.
Слайд 25Получим
и сравним
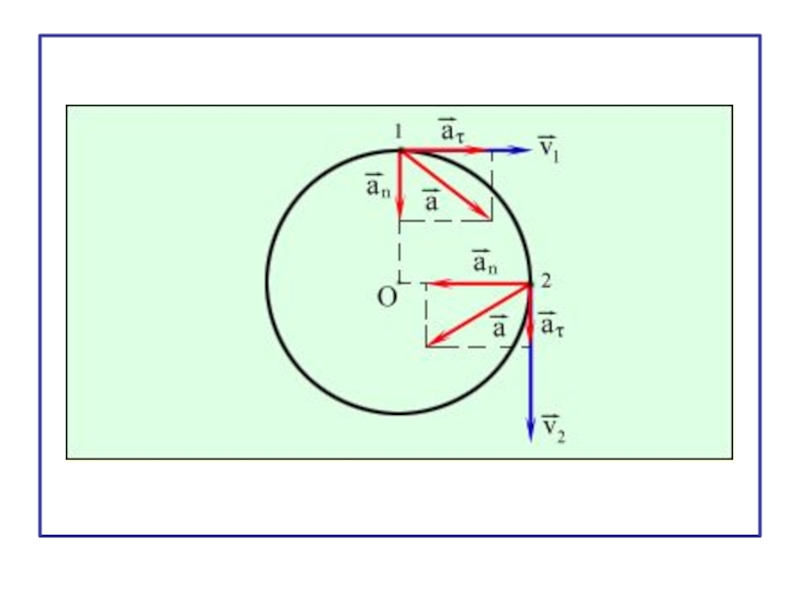
Первый вектор в правой части - тангенциальное ускорение.
Второй вектор –
нормальное ускорение.
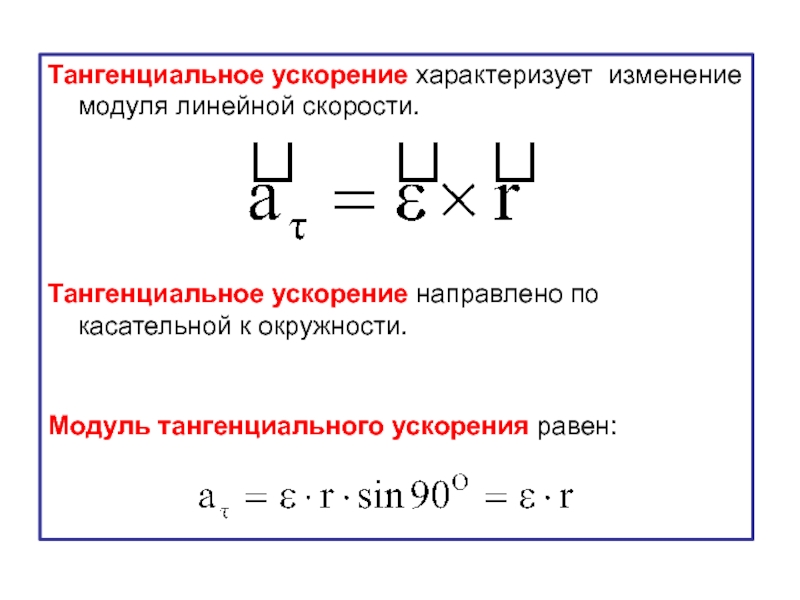
Слайд 26Тангенциальное ускорение характеризует изменение модуля линейной скорости.
Тангенциальное ускорение направлено по
касательной к окружности.
Модуль тангенциального ускорения равен:
Модуль тангенциального ускорения равен:
Слайд 27
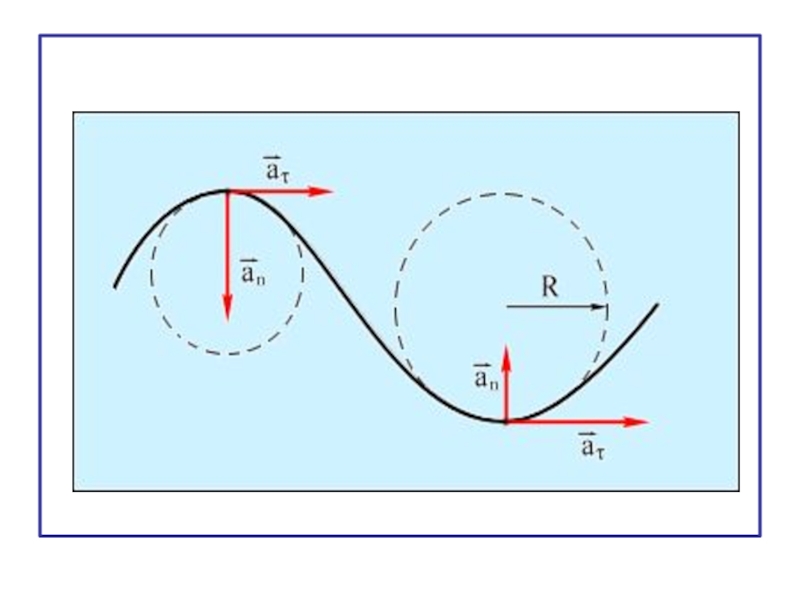
Нормальное ускорение характеризует изменение направления линейной скорости.
Нормальное ускорение направлено к центру
окружности.
Модуль нормального ускорения равен
Модуль нормального ускорения равен
