- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Структурное сопоставление трехмерных изображений и сезонно-суточная инвариантность презентация
Содержание
- 1. Структурное сопоставление трехмерных изображений и сезонно-суточная инвариантность
- 2. Авторы: Луцив Вадим Ростиславович, Малашин
- 3. Содержание доклада Практическая актуальность задачи сопоставления
- 4. Практическая актуальность задачи сопоставления изображений Многие годы
- 5. Традиционные методы распознавания не достаточно эффективны в
- 6. Известный современный алгоритм SIFT ошибается при сопоставлении
- 7. Нашим коллективом ранее был разработан эффективный объектно-независимый
- 8. Надежность работы нашего алгоритма в условиях естественной
- 9. Направленный осветитель Маленькое зеркало Проекция метки зоны
- 10. E1-1: z=k1x2+k2y2+C=(k1x2+С1)
- 11. Выделение текселов
- 12. Февральский аэрофотоснимок Результат структурного сопоставления и регистрации
- 13. Структурное сопоставление радиолокационных и оптических снимков Радиолокационный
- 14. Космический снимок Векторная ГИС-карта местности Результат сопоставления
- 15. Грубый контурный набросок самолета, сделанный от руки
- 16. Исходные снимки Результат автоматического сопоставления и регистрации
- 17. Двумерное контурное структурное описание, используемое
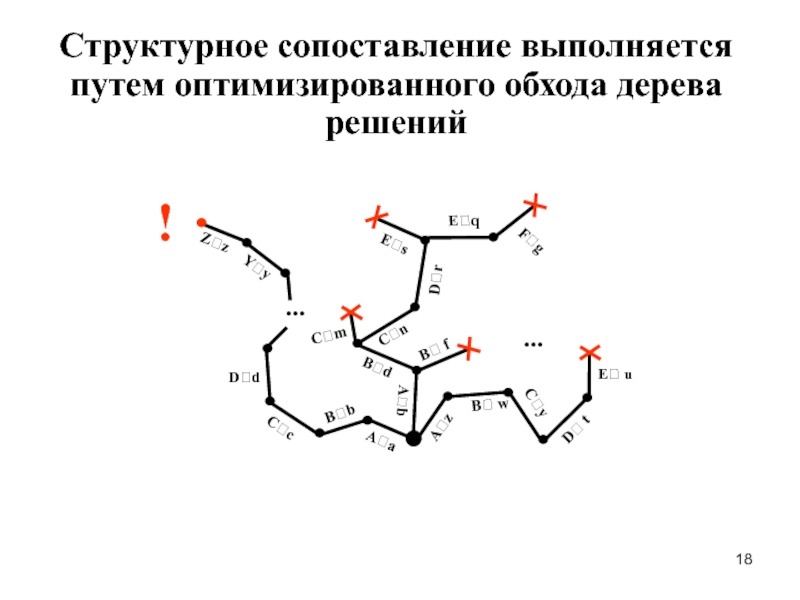
- 18. Структурное сопоставление выполняется путем оптимизированного обхода дерева решений
- 19. ? ? Структурное сопоставление
- 20. Коррекция групп элементов 2й иерархический
- 21. Коррекция контурных структурных описаний на нижнем иерархическом
- 22. Такое робастное сопоставление достигается именно за счет
- 23. Структурные описания
- 24. Нельзя применять единую модель геометрического преобразования
- 25. Структурные элементы 1го изображения
- 26. , . y
- 27. y x z 0 X1 X2
- 28. Переход от двумерной модели аффинного
- 29. Переход от двумерной модели проективного преобразования к
- 30. Пример модельных видеоданных, использованных в задаче трехмерного
- 31. Трехмерные видеоданные, реально полученные
- 32. Сравнительный
- 34. Замена трехмерной аффинной на трехмерную проективную модель
- 35. Пара сопоставляемых изображений трехмерной сцены
- 36. Чтобы убедиться в этом, необходимы подходящие наборы
- 37. Выводы Использование разработанного объектно-независимого подхода к
- 38. Благодарю за внимание
Слайд 2Авторы:
Луцив Вадим Ростиславович,
Малашин Роман Олегович, Малышев Игорь Александрович,
Государственный оптический институт им. С.И. Вавилова
Слайд 3Содержание доклада
Практическая актуальность задачи сопоставления изображений
Современные решения в области
Механизм двумерного структурного сопоставления, разработанный нами ранее
Усовершенствование механизма структурного сопоставления для обработки изображений трехмерных сцен
Результаты трехмерного структурного сопоставления и выводы
Слайд 4Практическая актуальность задачи сопоставления изображений
Многие годы алгоритмы сопоставления изображений применяются в:
здравоохранении
системах обеспечения безопасности и криминалистике
дистанционном зондировании Земли
Особенно сложно автоматическое сопоставление изображений реального естественного окружения, поэтому остается актуальной разработка новых робастных решений для:
распознавания целей
аэрокосмического мониторинга Земли
навигации беспилотных летательных аппаратов
навигации автономных наземных роботов
Наше исследование как раз посвящено алгоритмам сопоставления изображений реального естественного окружения.
Слайд 5Традиционные методы распознавания не достаточно эффективны в условиях естественной изменчивости и
Кросскорреляционная функция снимков, сделанных в разные сезоны или с разных ракурсов деградирует
Снимки одной и той же местности, сделанные с интервалом в несколько месяцев
Слайд 6Известный современный алгоритм SIFT ошибается при сопоставлении элементов изображений со слабо
Для преодоления этой трудности необходим более эффективный анализ взаимного положения элементов изображения!
Слайд 7Нашим коллективом ранее был разработан эффективный объектно-независимый алгоритм контурного структурного сопоставления
Исходное изображение
Контуры, относящиеся к большим градиентам яркости
Структурное описание контуров
Слайд 8Надежность работы нашего алгоритма в условиях естественной изменчивости окружающей среды обусловлена
Большинство систем машинного зрения проецируют изображение через линзу, что является источником проективных или аффинных преобразований.
Объекты наблюдаемого мира обычно локально жесткие. Взаимное положение их частей не изменяется мгновенно. Нежесткость объектов приводит к отклонениям преобразования их изображений от аффинного.
Объекты наблюдаемого мира, обычно не прозрачны, а их поверхности не зеркальны. Наблюдение прозрачных и зеркально отраженных объектов часто связано со зрительными иллюзиями.
Наблюдаемый мир состоит из поверхностей объектов, что в совокупности с непрозрачностью обусловливает правила загораживания объектов.
Свойства поверхностей варьируют при изменении условий наблюдения. Наблюдаемые границы объектов наиболее устойчивы к таким изменениям.
Наблюдаемый мир структурирован и организован иерархически: видимая сцена делится на объекты и подобъекты. При увеличении пространственного разрешения текселы также становятся объектами, имеющими свою форму.
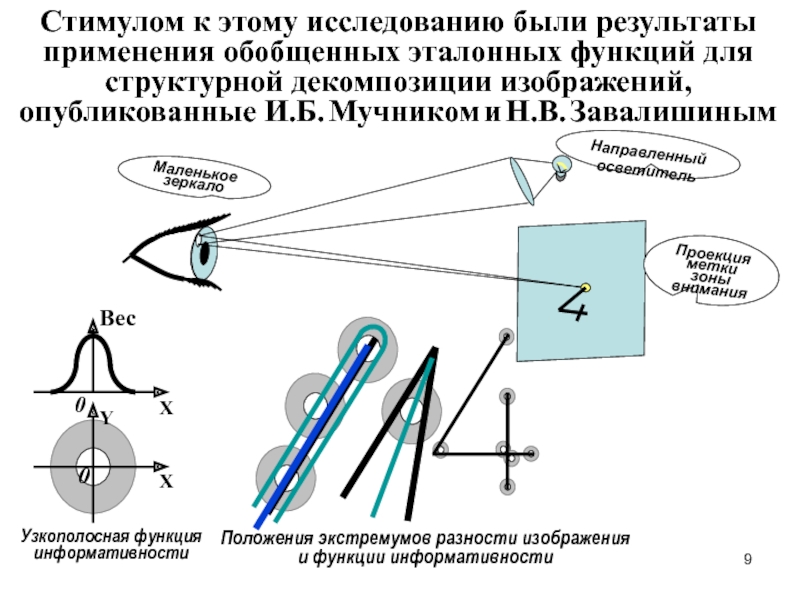
Слайд 9Направленный осветитель
Маленькое зеркало
Проекция метки зоны внимания
Вес
Y
X
X
0
0
Узкополосная функция информативности
Положения экстремумов разности изображения
Стимулом к этому исследованию были результаты применения обобщенных эталонных функций для структурной декомпозиции изображений, опубликованные И.Б. Мучником и Н.В. Завалишиным
Слайд 10
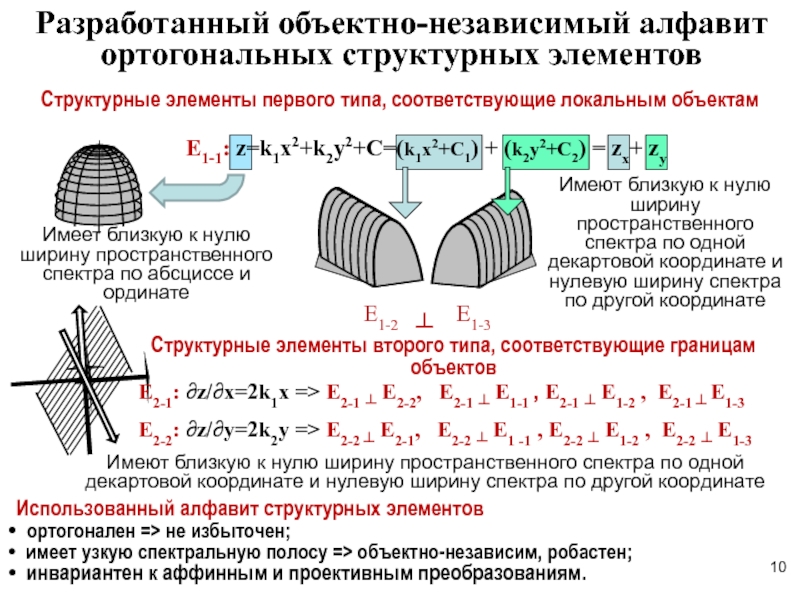
E1-1: z=k1x2+k2y2+C=(k1x2+С1) + (k2y2+C2) = zx+ zy
Структурные элементы первого типа, соответствующие
E2-1: ∂z/∂x=2k1x => E2-1 ┴ E2-2, E2-1 ┴ E1-1 , E2-1 ┴ E1-2 , E2-1 ┴ E1-3
E2-2: ∂z/∂y=2k2y => E2-2 ┴ E2-1, E2-2 ┴ E1 -1 , E2-2 ┴ E1-2 , E2-2 ┴ E1-3
Структурные элементы второго типа, соответствующие границам объектов
Имеет близкую к нулю ширину пространственного спектра по абсциссе и ординате
Имеют близкую к нулю ширину пространственного спектра по одной декартовой координате и нулевую ширину спектра по другой координате
Имеют близкую к нулю ширину пространственного спектра по одной декартовой координате и нулевую ширину спектра по другой координате
Е1-2 ┴ Е1-3
Использованный алфавит структурных элементов
ортогонален => не избыточен;
имеет узкую спектральную полосу => объектно-независим, робастен;
инвариантен к аффинным и проективным преобразованиям.
Разработанный объектно-независимый алфавит ортогональных структурных элементов
Слайд 11
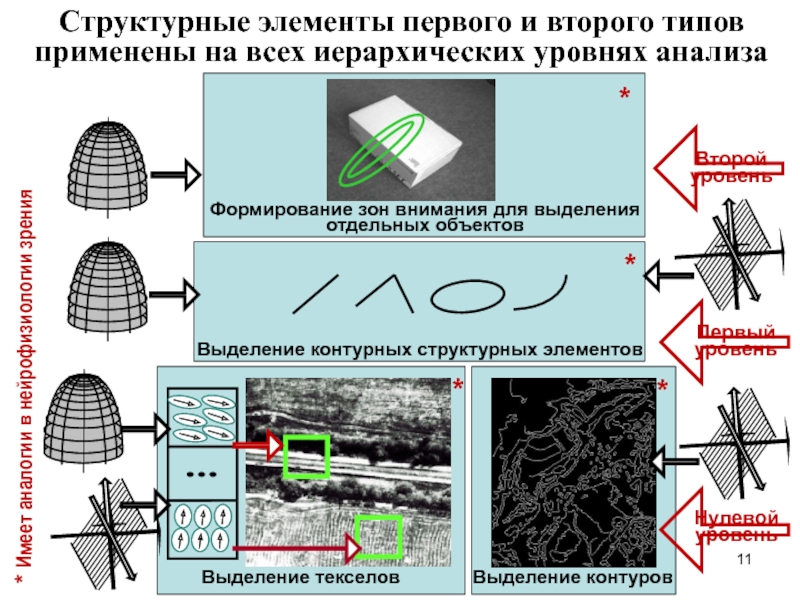
Выделение текселов
Выделение контуров
Выделение контурных структурных элементов
Формирование зон внимания для выделения отдельных
Нулевой уровень
Первый уровень
Второй уровень
* Имеет аналогии в нейрофизиологии зрения
*
*
*
*
Структурные элементы первого и второго типов применены на всех иерархических уровнях анализа
Слайд 12Февральский аэрофотоснимок
Результат структурного сопоставления и регистрации снимков
Механизм двумерного анализа пригоден для
Майский снимок той же местности
Слайд 13Структурное сопоставление радиолокационных и оптических снимков
Радиолокационный снимок
Снимок, сделанный в оптическом диапазоне
Результат
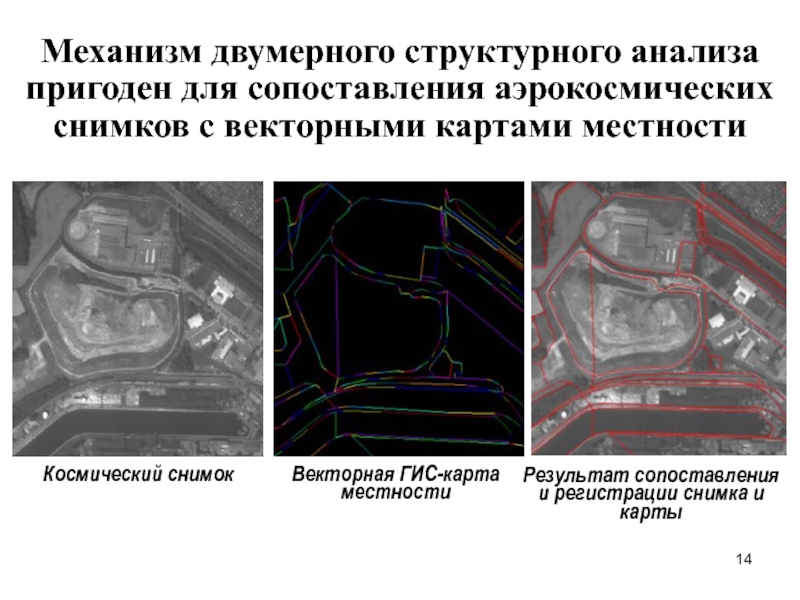
Слайд 14Космический снимок
Векторная ГИС-карта местности
Результат сопоставления и регистрации снимка и карты
Механизм двумерного
Слайд 15Грубый контурный набросок самолета, сделанный от руки
Реальное растровое изображение самолета
Результат сопоставления
Контуры, выделенные в растровом изображении
Механизм двумерного структурного анализа пригоден для сопоставления реальных снимков с контурными скетчами
Слайд 16Исходные снимки
Результат автоматического сопоставления и регистрации снимков
«Способности к обобщению» в
Алгоритм SIFT не способен к таким зрительным ассоциациям!
Слайд 17
Двумерное контурное структурное описание, используемое при сопоставлении изображений
Структурные описания включают огромные
Исходное полутоновое изображение
Контуры, относящиеся к большим градиентам яркости
Контурное структурное описание
Слайд 19?
?
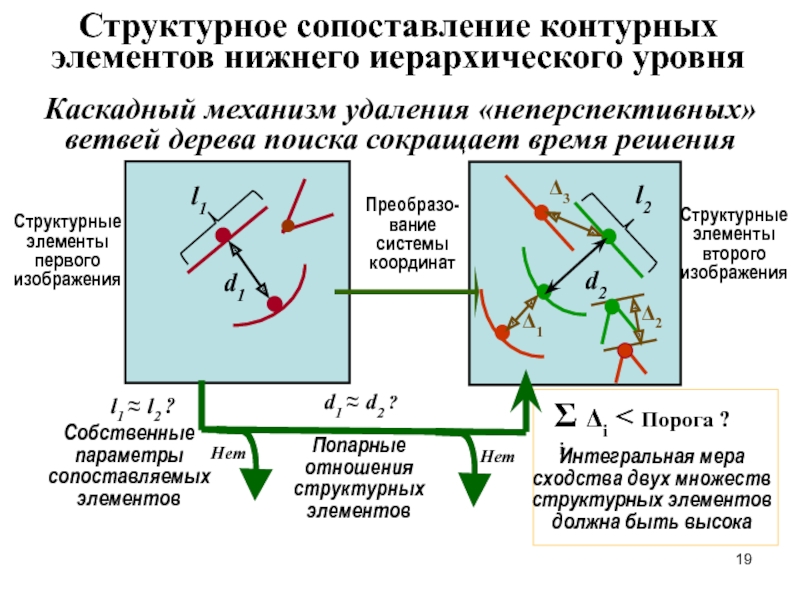
Структурное сопоставление контурных элементов нижнего иерархического уровня
Каскадный механизм удаления
Структурные элементы первого изображения
Структурные элементы второго изображения
d1
l1
d2
l2
Δ3
Δ2
Δ1
d1 ≈ d2 ?
Преобразо-вание системы координат
l1 ≈ l2 ?
Собственные параметры сопоставляемых элементов
Попарные отношения структурных элементов
Интегральная мера сходства двух множеств структурных элементов должна быть высока
Σ Δi < Порога ?
i
Нет
Нет
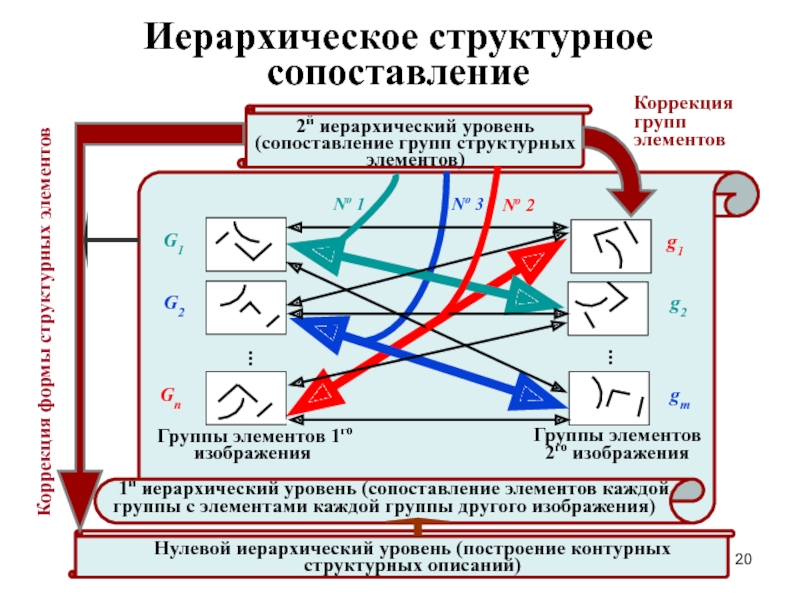
Слайд 20Коррекция групп элементов
2й иерархический уровень (сопоставление групп структурных элементов)
1й
Нулевой иерархический уровень (построение контурных структурных описаний)
Коррекция формы структурных элементов
a
b
G1
G2
Gn
g1
g2
gm
Группы элементов 1го изображения
Группы элементов 2го изображения
...
...
No 1
No 3
No 2
Иерархическое структурное сопоставление
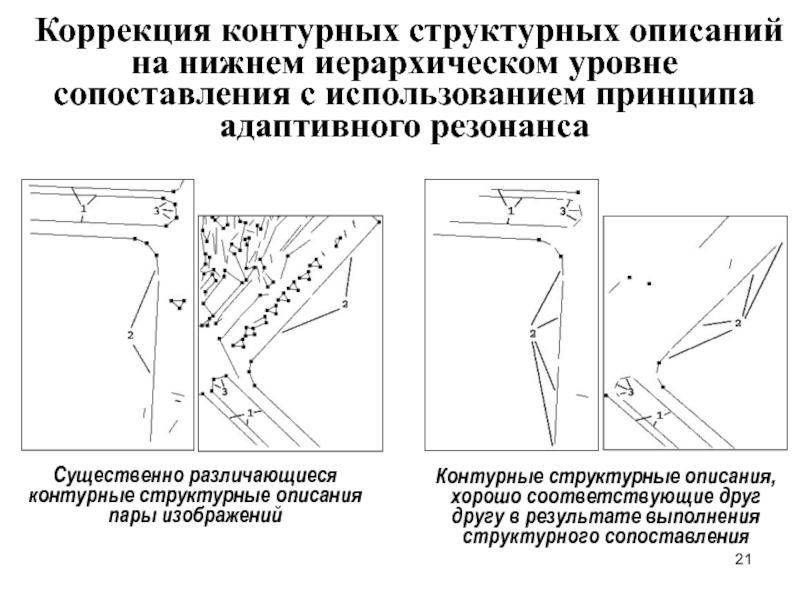
Слайд 21Коррекция контурных структурных описаний на нижнем иерархическом уровне сопоставления с использованием
Существенно различающиеся контурные структурные описания пары изображений
Контурные структурные описания, хорошо соответствующие друг другу в результате выполнения структурного сопоставления
Слайд 22Такое робастное сопоставление достигается именно за счет применения иерархической процедуры с
Радиолокационный снимок
Снимок, сделанный в оптическом диапазоне
Результат сопоставления и мозаичной регистрации снимков
Слайд 23
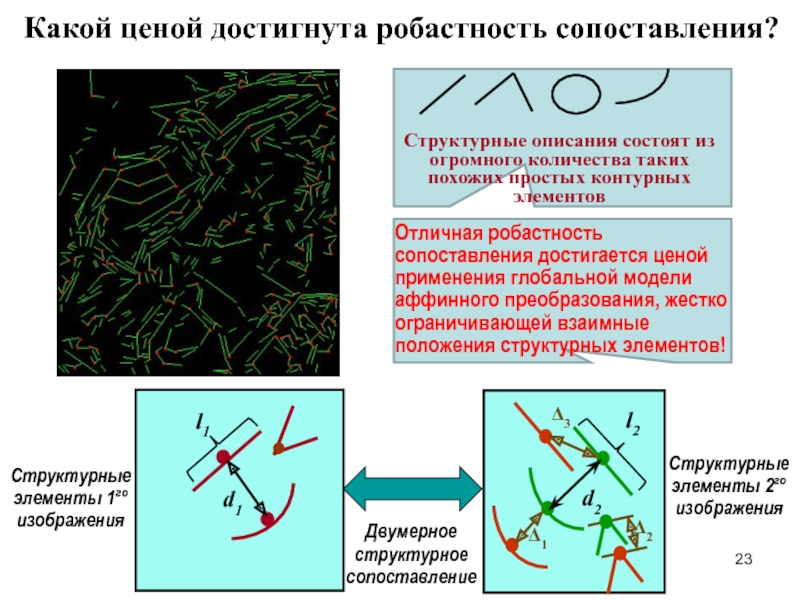
Структурные описания состоят из огромного количества таких похожих простых контурных элементов
Какой
Структурные элементы 1го изображения
d1
l1
d2
l2
Δ3
Δ2
Δ1
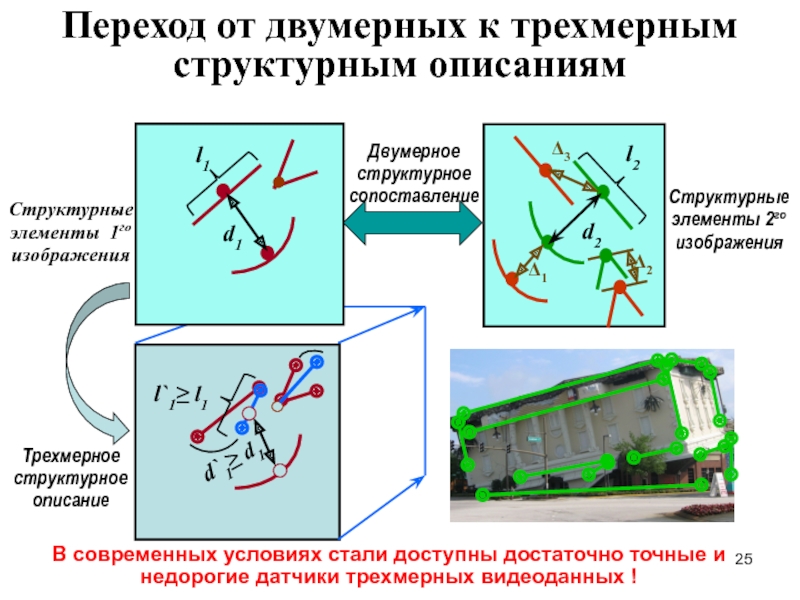
Двумерное структурное сопоставление
Структурные элементы 2го изображения
Отличная робастность сопоставления достигается ценой применения глобальной модели аффинного преобразования, жестко ограничивающей взаимные положения структурных элементов!
Слайд 24
Нельзя применять единую модель геометрического преобразования к всему изображению трехмерной сцены
Изображение
Преобразование изображения должно быть описано отдельной моделью для каждой наблюдаемой поверхности
Слайд 25Структурные элементы 1го изображения
l`1≥ l1
d1
l1
d2
l2
Δ3
Δ2
Δ1
Двумерное структурное сопоставление
Структурные элементы 2го изображения
Трехмерное структурное
d`1≥ d1
Переход от двумерных к трехмерным структурным описаниям
В современных условиях стали доступны достаточно точные и недорогие датчики трехмерных видеоданных !
Слайд 26
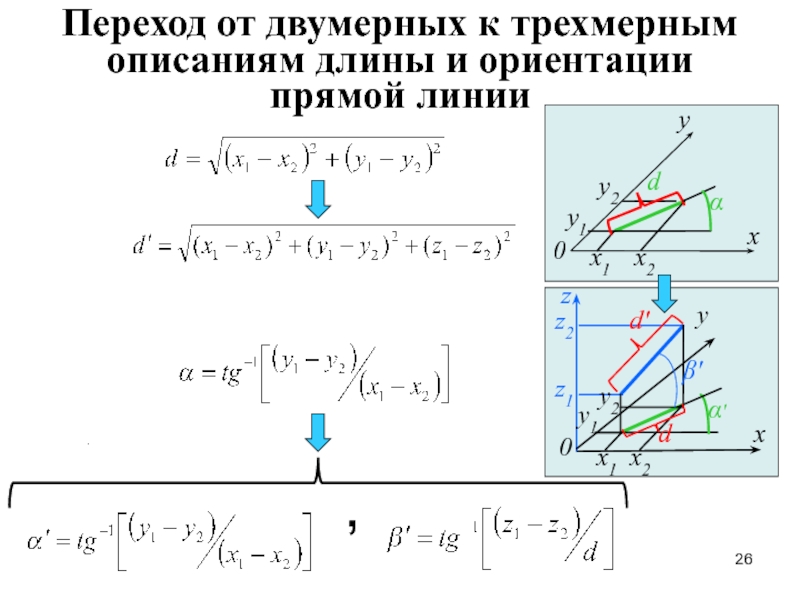
,
.
y
x
0
x1
x2
y1
y2
d
α
y
x
z
0
x1
x2
y2
y1
z1
z2
d'
β'
Переход от двумерных к трехмерным описаниям длины и ориентации прямой линии
α'
d
Слайд 27
y
x
z
0
X1
X2
δ
(x1, y1, z1)T
(x2, y2, z2)T
(x3, y3, z3)T
(x4, y4, z4)T
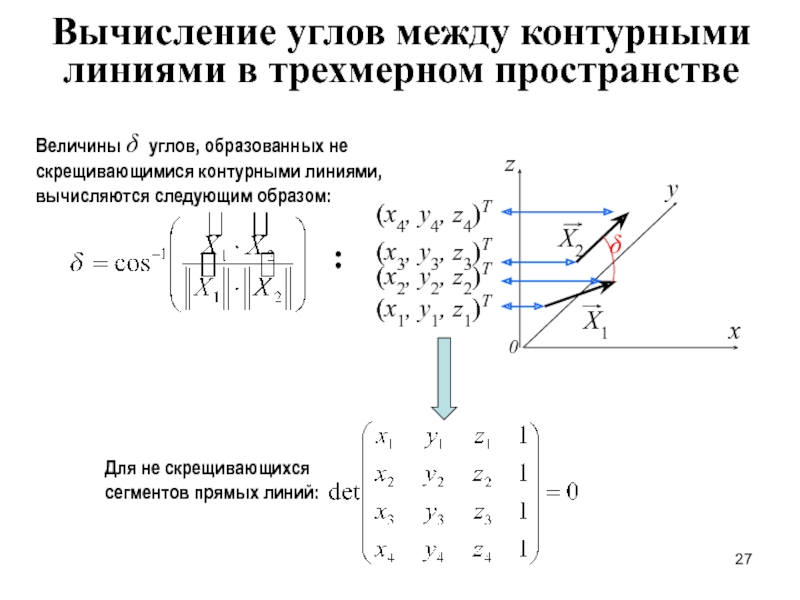
Вычисление углов между
:
Величины δ углов, образованных не скрещивающимися контурными линиями, вычисляются следующим образом:
Для не скрещивающихся сегментов прямых линий:
Слайд 28
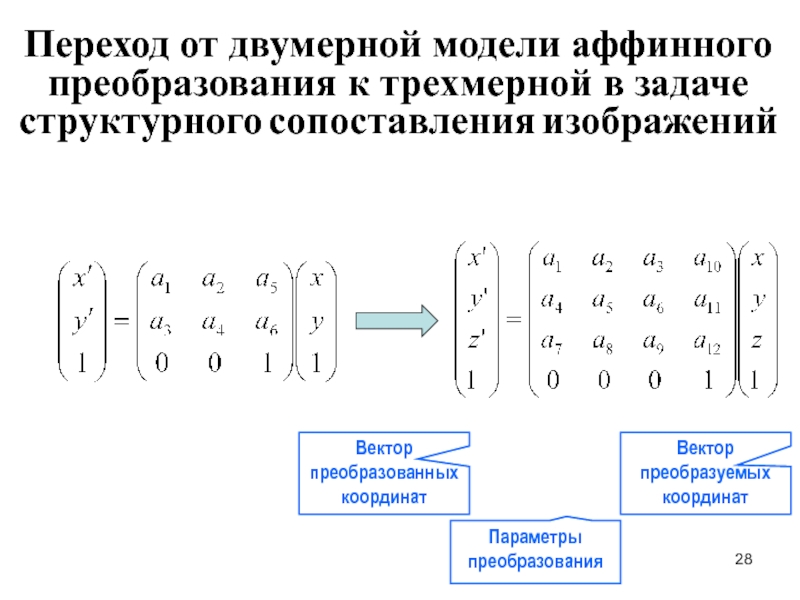
Переход от двумерной модели аффинного преобразования к трехмерной в задаче структурного
Вектор преобразованных координат
Параметры преобразования
Вектор преобразуемых координат
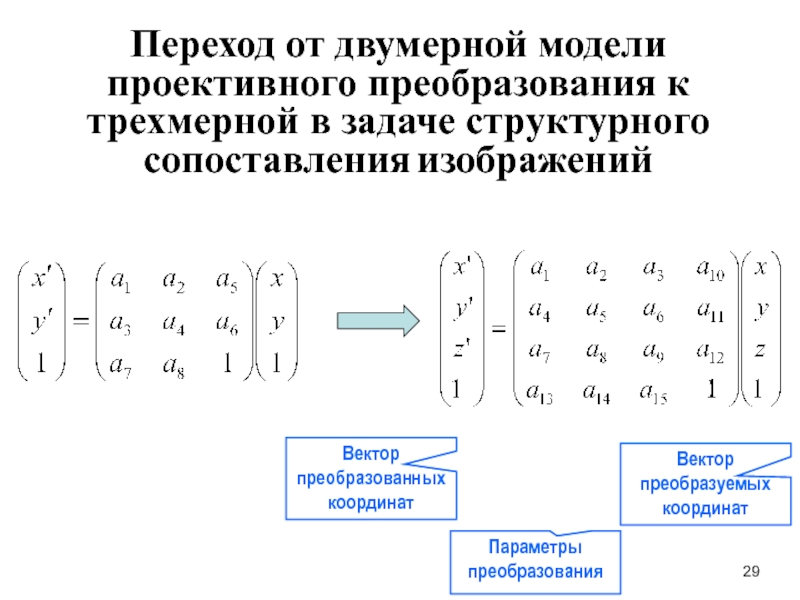
Слайд 29Переход от двумерной модели проективного преобразования к трехмерной в задаче структурного
Вектор преобразованных координат
Вектор преобразуемых координат
Параметры преобразования
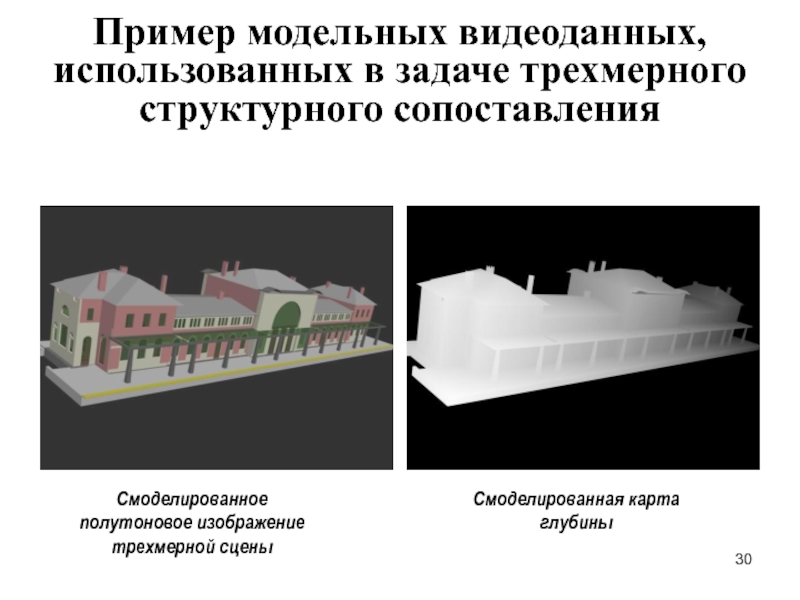
Слайд 30Пример модельных видеоданных, использованных в задаче трехмерного структурного сопоставления
Смоделированное полутоновое изображение
Смоделированная карта глубины
Слайд 31
Трехмерные видеоданные, реально полученные сенсором Kinect в помещении с разных ракурсов
Карты
Двумерные изображения
Контуры, выделенные в двумерных изображениях
Слайд 32
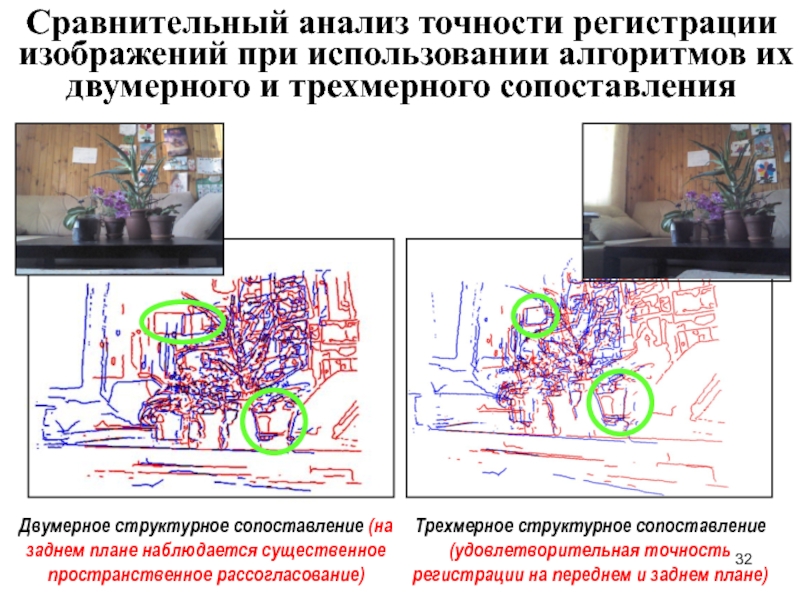
Сравнительный анализ точности регистрации изображений при использовании алгоритмов их двумерного и
Двумерное структурное сопоставление (на заднем плане наблюдается существенное пространственное рассогласование)
Трехмерное структурное сопоставление (удовлетворительная точность регистрации на переднем и заднем плане)
Слайд 33
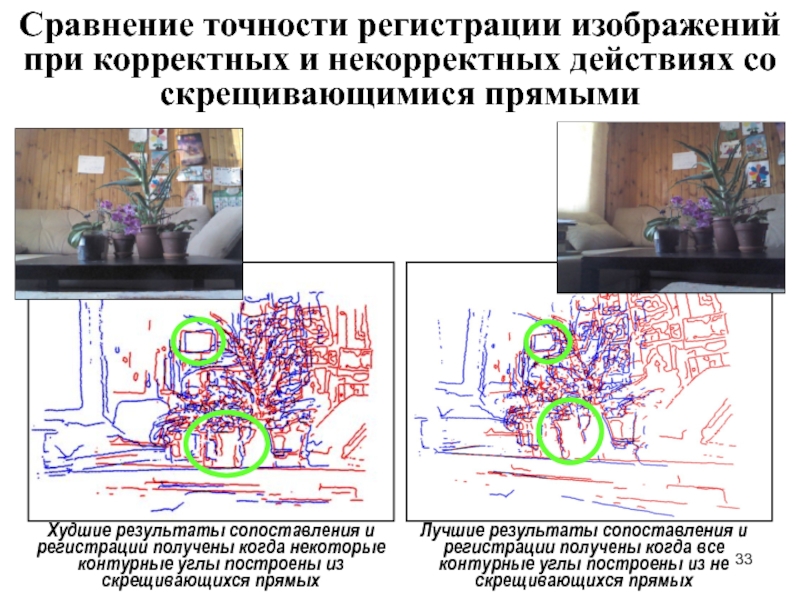
Сравнение точности регистрации изображений при корректных и некорректных действиях со скрещивающимися
Лучшие результаты сопоставления и регистрации получены когда все контурные углы построены из не скрещивающихся прямых
Худшие результаты сопоставления и регистрации получены когда некоторые контурные углы построены из скрещивающихся прямых
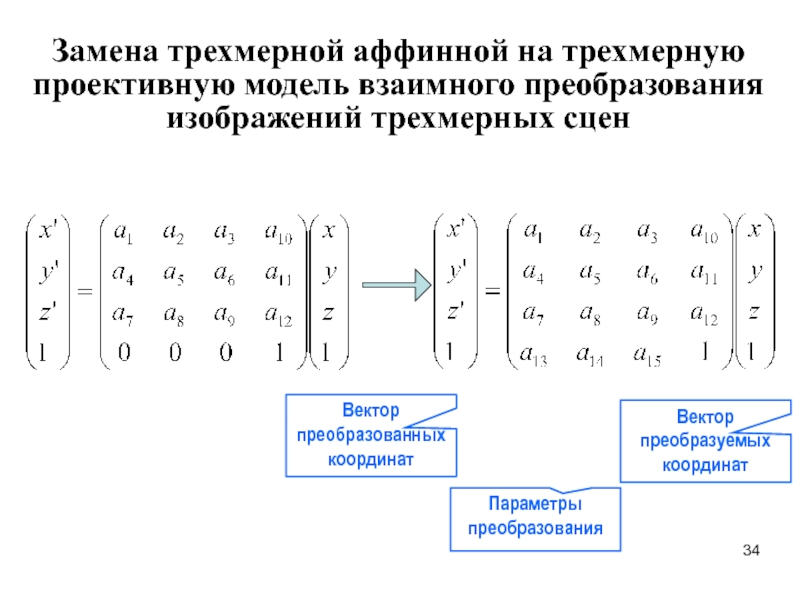
Слайд 34Замена трехмерной аффинной на трехмерную проективную модель взаимного преобразования изображений трехмерных
Вектор преобразованных координат
Вектор преобразуемых координат
Параметры преобразования
Слайд 35
Пара сопоставляемых изображений трехмерной сцены
Улучшение точности сопоставления контуров с применением проективной
Проективная модель преобразования
Аффинная модель преобразования
Слайд 36Чтобы убедиться в этом, необходимы подходящие наборы трехмерных видеоданных, полученных на
Отличные возможности обобщения, полученные ранее для нашего механизма двумерного сопоставления, должны сохраниться в случае трехмерного сопоставления
?
Слайд 37Выводы
Использование разработанного объектно-независимого подхода к контурному структурному анализу и заимствование
Результаты работы алгоритма трехмерного структурного сопоставления заметно лучше результатов двумерного сопоставления. Это подтверждает корректность используемых математических моделей.
Использование модели трехмерного проективного преобразования вместо модель трехмерного аффинного преобразования увеличило точность структурного сопоставления.
Наконец, необходимо перейти к анализу трехмерных видеоданных, реально полученных на открытом воздухе.