- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Строительная механика. Расчёт сооружений на действие подвижных и других временных нагрузок. Теория линий влияния презентация
Содержание
- 1. Строительная механика. Расчёт сооружений на действие подвижных и других временных нагрузок. Теория линий влияния
- 2. Временными воздействиями (нагрузками) называются такие,
- 3. Основные задачи расчёта сооружения (конструкции) на
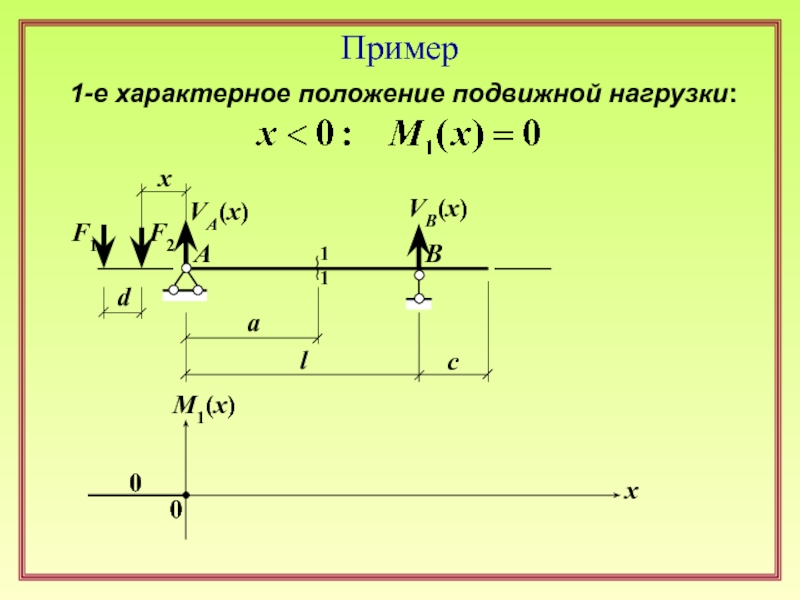
- 4. Пример
- 5. Пример
- 6. Пример
- 7. Пример
- 8. Пример
- 12. Пример - результаты
- 13. Возможный вариант:
- 14. Линией влияния некоторого фактора НДС
- 18. Различия между линией влияния и эпюрой
- 19. К о н т р о л
Слайд 1
Расчёт сооружений
на действие подвижных
и других временных
нагрузок
СТРОИТЕЛЬНАЯ МЕХАНИКА.
Часть I
С
ВГ
ТЕОРИЯ
Слайд 2Временными воздействиями (нагрузками) называются такие, действие которых на сооружение (конструкцию) ограничено во
Подвижными называются
временные нагрузки, место и/или область приложения которых
на сооружении (конструкции) изменяются.
Слайд 3Основные задачи расчёта сооружения (конструкции)
на действие подвижной нагрузки
1. Выявление закона
напряжённо-деформированного состояния (НДС) системы (реакции внешней или внутренней связи, внутреннего
силового фактора – усилия или напряжения в сечении, перемещения, деформации и др.) в зависимости от
характеристик (координат) положения подвижной нагрузки на сооружении (конструкции).
2. Определение экстремальных значений (максимального и минимального)
исследуемого фактора и соответствующих им положений нагрузки, называемых
невыгоднейшими (опасными) положениями
подвижной нагрузки.
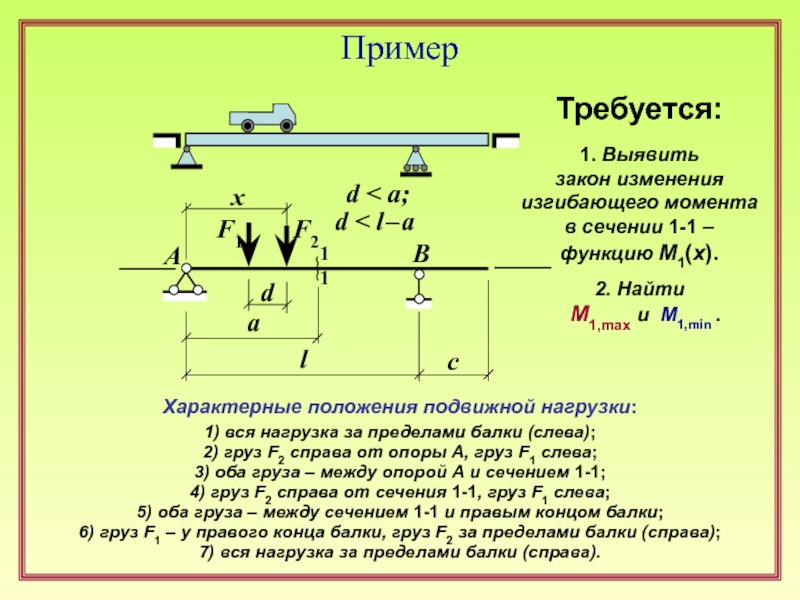
Слайд 4Пример
Требуется:
1. Выявить
закон изменения
изгибающего момента
в сечении 1-1 –
функцию М1(х).
2. Найти
F1
F2
l
d
a
c
x
1
1
Характерные положения подвижной нагрузки:
1) вся нагрузка за пределами балки (слева);
2) груз F2 справа от опоры А, груз F1 слева;
3) оба груза – между опорой А и сечением 1-1;
4) груз F2 справа от сечения 1-1, груз F1 слева;
5) оба груза – между сечением 1-1 и правым концом балки;
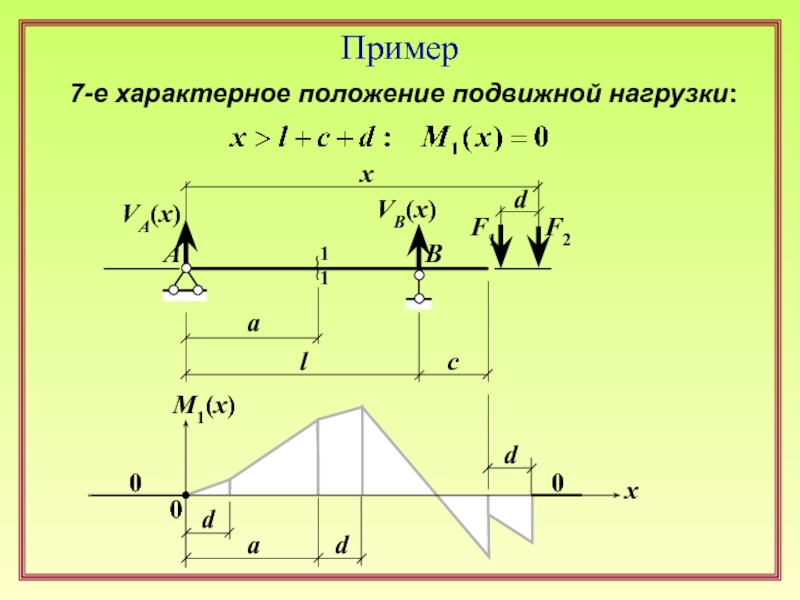
6) груз F1 – у правого конца балки, груз F2 за пределами балки (справа);
7) вся нагрузка за пределами балки (справа).
d < a;
d < l – a
A
B
Слайд 6Пример
F1
F2
l
d
a
c
x
1
1
A
B
VA(x)
VB(x)
x
M1(x)
0
2-е характерное положение подвижной нагрузки:
d
F2d (1 – a/l )
0
Слайд 7Пример
F1
F2
l
d
a
c
x
1
1
A
B
VA(x)
VB(x)
x
M1(x)
3-е характерное положение подвижной нагрузки:
d
F2d (1 – a/l )
0
a
0
[F2a +F1(a –
Слайд 8Пример
F1
F2
l
d
a
c
x
1
1
A
B
VA(x)
VB(x)
x
M1(x)
4-е характерное положение подвижной нагрузки:
d
F2d (1 – a/l )
0
a
d
0
[F2a +F1(a –
[(F2 +F1)(l – a) – F2d ] a/l
Слайд 9
F1
F2
l
d
a
c
x
1
1
A
B
VA(x)
VB(x)
x
M1(x)
5-е характерное положение подвижной нагрузки:
d
[F2c +F1(c – d )]a/l
0
a
d
0
[(F2 +F1)(l –
Пример
Слайд 10
F1
F2
l
d
a
c
x
1
1
A
B
VA(x)
VB(x)
x
M1(x)
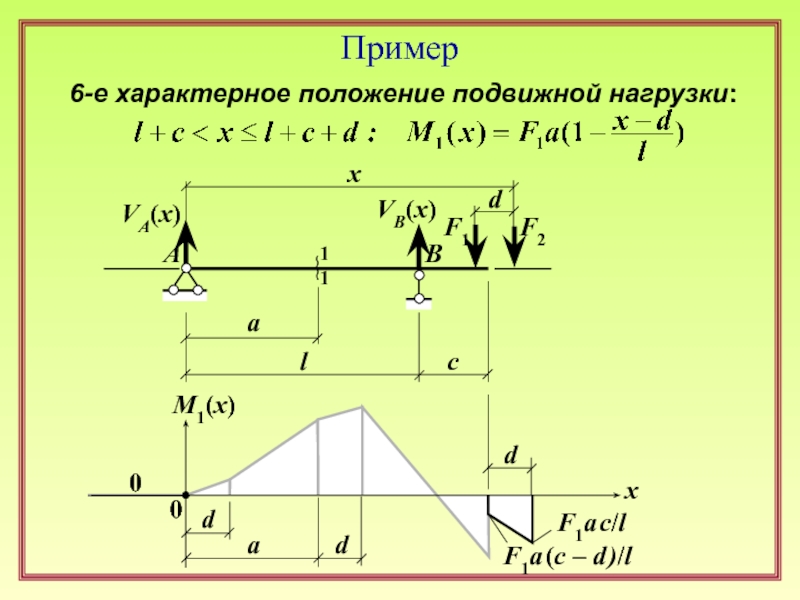
6-е характерное положение подвижной нагрузки:
d
F1a (c – d )/l
0
a
d
d
0
Пример
F1a c/l
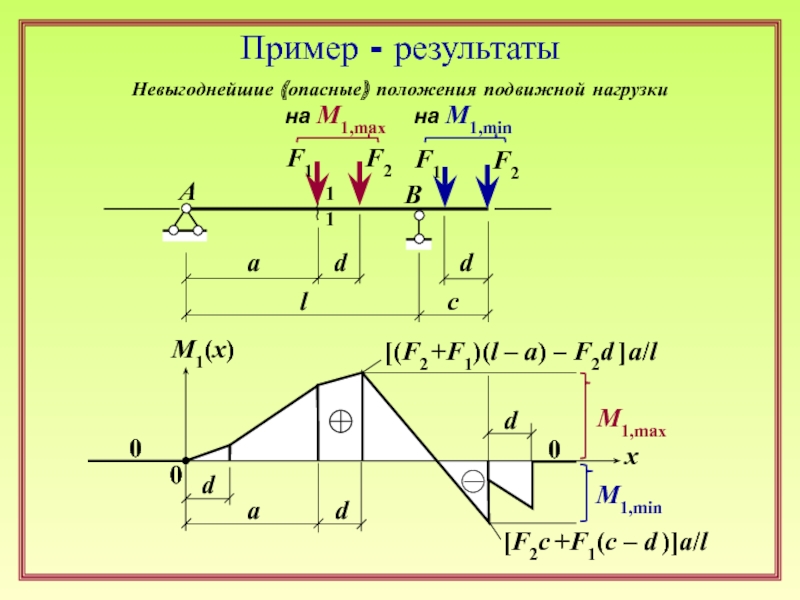
Слайд 12Пример - результаты
F1
F2
l
d
a
c
1
1
A
B
x
M1(x)
d
0
a
d
d
0
d
F1
F2
на М1,max
на М1,min
Невыгоднейшие (опасные) положения подвижной нагрузки
0
М1,max
М1,min
[(F2
[F2c +F1(c – d )]a/l
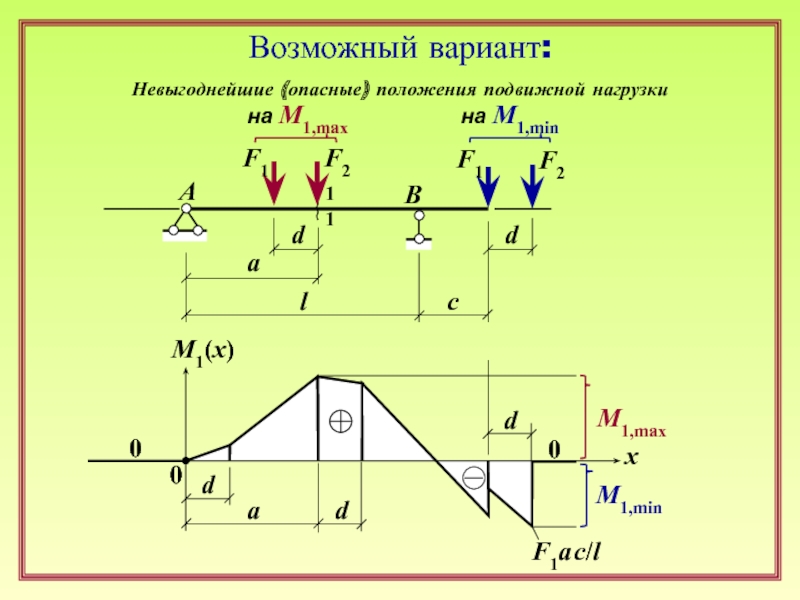
Слайд 13Возможный вариант:
F1
F2
l
d
a
c
1
1
A
B
x
M1(x)
d
0
a
d
d
0
d
F1
F2
на М1,max
на М1,min
Невыгоднейшие (опасные) положения подвижной нагрузки
0
М1,max
М1,min
F1a c/l
Слайд 14Линией влияния
некоторого фактора НДС
Примечания:
1. Функция, выражающая зависимость
некоторого фактора НДС от
точки приложения единичного подвижного груза F = 1,
называется функцией влияния данного фактора.
2. Единичный груз F = 1 – безразмерный.
называется график функции,
выражающей зависимость данного фактора
от координат(ы) точки приложения
одиночного единичного подвижного груза ( F = 1 ), сохраняющего неизменное направление
линии действия при перемещении
по сооружению (конструкции).
Идея – E. Winkler ( 1867 г. )
Слайд 15
F = 1
l
a
c
x
1
1
A
B
VA(x)
VB(x)
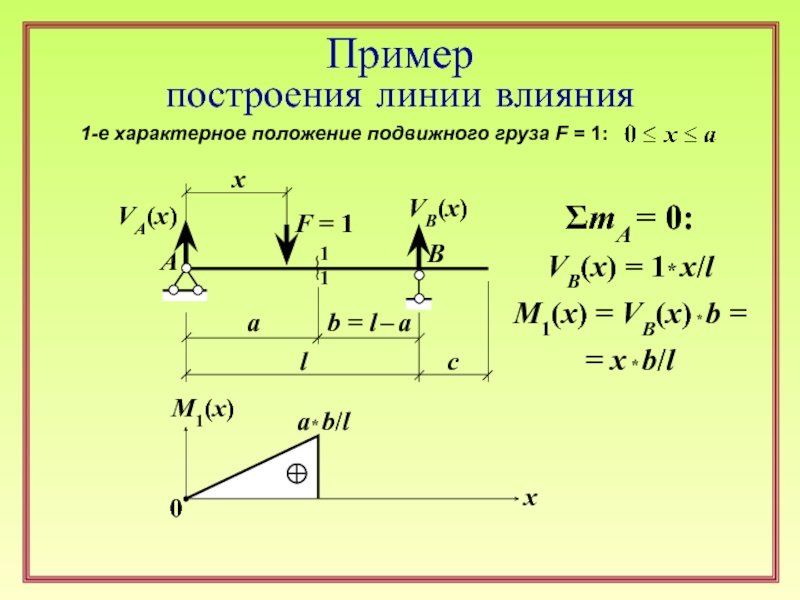
Пример
построения линии влияния
Требуется:
Построить
линию влияния
изгибающего момента
в сечении 1 –
( Л.В. М1 ).
Характерные положения единичного подвижного груза:
1) груз F = 1 слева от сечения 1 – 1 ( );
2) груз F = 1 справа от сечения 1 – 1 ( );
Слайд 16
F = 1
l
a
c
x
1
1
A
B
VA(x)
VB(x)
Пример
построения линии влияния
ΣmA = 0:
VB(x) = 1* x/l
M1(x) =
= x * b/l
1-е характерное положение подвижного груза F = 1:
b = l – a
0
M1(x)
x
a* b/l
Слайд 17
F = 1
l
a
c
x
1
1
A
B
VA(x)
VB(x)
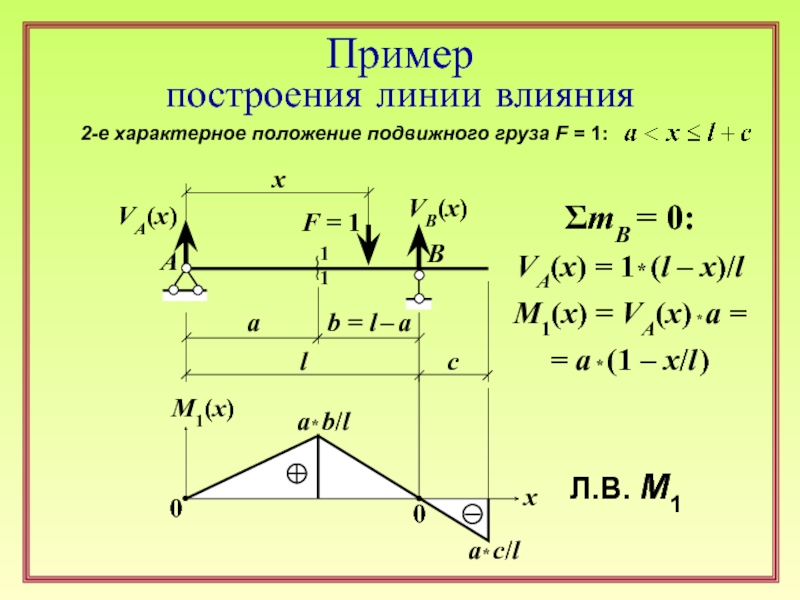
Пример
построения линии влияния
ΣmB = 0:
VA(x) = 1* (l –
M1(x) = VA(x) * a =
= a * (1 – x/l )
2-е характерное положение подвижного груза F = 1:
b = l – a
0
M1(x)
x
a* b/l
0
a* c/l
Л.В. М1
Слайд 18Различия
между линией влияния и эпюрой
От какой нагрузки
строится
От условной одиночной подвижной
равной безразмерной
единице (F=1)
От реальной неподвижной нагрузки, возможно много-компонентной, определённым образом расположенной
на сооружении
Что показывает
в целом
Значения исследуемого фактора при разных положениях единичного подвижного груза F=1
Значения исследуемого фактора в разных точках (сечениях) системы при фиксированной нагрузке
Смысл
произвольной
ординаты
Значение исследуемого фактора при расположе-нии единичного груза F=1 в том месте, где читается ордината
Что позволяет
определить
Невыгоднейшие (опасные) положения реальных подвиж-ных и других временных нагрузок и соответствующие экстремальные значения
исследуемого фактора
Точки (опасные сечения) системы и экстремальные значения исследуемого фактора в них при фиксированной нагрузке
Значение исследуемого фактора в том месте (сечении), где читается ордината
Слайд 19К о н т р о л ь н ы е
( в скобках даны номера слайдов, на которых можно найти ответы на вопросы;
для перехода к слайду с ответом можно сделать щелчок мышью по номеру в скобках*);
для возврата к контрольным вопросам сделать щелчок правой кнопкой мыши
и выбрать «Перейти к слайду 19» )
1. Какие воздействия на сооружения ( конструкции ) относятся к временным? ( 2 )
2. Какие нагрузки называются подвижными? ( 2 )
3. Каковы основные задачи расчёта сооружения ( конструкции) на действие
подвижной нагрузки? ( 3 )
4. Что такое невыгоднейшее ( опасное ) положение подвижной нагрузки? ( 3 )
5. В чём трудность непосредственного расчёта на заданную подвижную нагрузку? ( 4 – 13 )
6. Для чего в расчётах на временные воздействия используются специальные функции
и графики ( функции и линии влияния )? ( самостоятельно )
7. Что такое линия влияния и функция влияния некоторого фактора НДС системы? ( 14 )
8. Что является аргументом функции и линии влияния? ( 14 )
9. От какого воздействия строится линия влияния некоторого фактора НДС? ( 14 )
10. Почему в общем случае функция и линия влияния являются кусочными ( имеют
разные аналитические выражения на разных участках )? ( 15 – 17 )
11. Каковы основные различия между линией влияния и эпюрой некоторого силового фактора? ( 18 )
12. Можно ли построить линию влияния некоторой опорной реакции? А её эпюру? ( 18 )
13. Какой смысл имеет отдельная ордината линии влияния? ( 18 )
14. Какие задачи расчёта сооружения ( конструкции ) можно решать с помощью линий влияния? ( 18 )
_____________________________________________________
*) Только в режиме «Показ слайдов»




![ПримерF1F2ldacx11ABVA(x)VB(x)xM1(x)3-е характерное положение подвижной нагрузки:dF2d (1 – a/l )0a0[F2a +F1(a – d )] (1 –](/img/tmb/4/332337/3af474e445bf14695ca8f601f662a848-800x.jpg)
![ПримерF1F2ldacx11ABVA(x)VB(x)xM1(x)4-е характерное положение подвижной нагрузки:dF2d (1 – a/l )0ad0[F2a +F1(a – d )] (1 –](/img/tmb/4/332337/d8b15f1a995763af973773a329aea48f-800x.jpg)
![F1F2ldacx11ABVA(x)VB(x)xM1(x)5-е характерное положение подвижной нагрузки:d[F2c +F1(c – d )]a/l0ad0[(F2 +F1)(l – a) – F2d ] a/lПример](/img/tmb/4/332337/7709ea00dea9707d5b90c1bc425541a0-800x.jpg)