- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Статистический и термодинамический методы презентация
Содержание
- 1. Статистический и термодинамический методы
- 2. Лекция № 1 1. Состояние термодинамического равно-
- 3. СТАТИСТИЧЕСКИЙ И ТЕРМО- ДИНАМИЧЕСКИЙ МЕТОДЫ
- 5. ТЕРМОДИНАМИЧЕСКАЯ СИСТЕМА. ПАРАМЕТРЫ СОСТОЯНИЯ Термодинамической
- 6. РАВНОВЕСНЫЕ И НЕРАВНОВЕСНЫЕ СОСТОЯНИЯ Параметры состояния
- 7. РАВНОВЕСНЫЕ ПРОЦЕССЫ Термодинамическим процессом называется переход
- 8. Состояние термодинамической системы, не изменяющееся во
- 9. ТЕМПЕРАТУРА Если два тела находятся
- 10. В физике и технике за абсолютную шкалу
- 11. Абсолютная температура Т не может
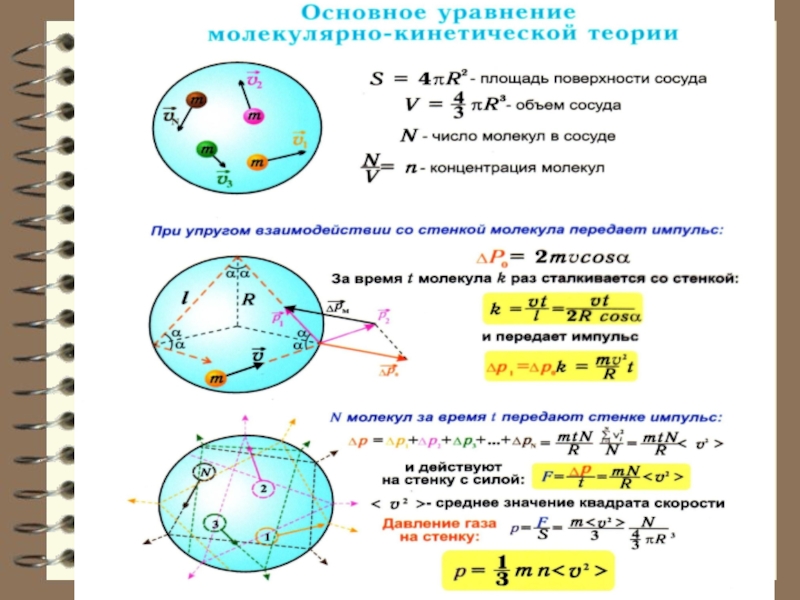
- 13. Давление. Основное уравнение молекулярно-кинетической теории
- 14. Находящиеся под давлением
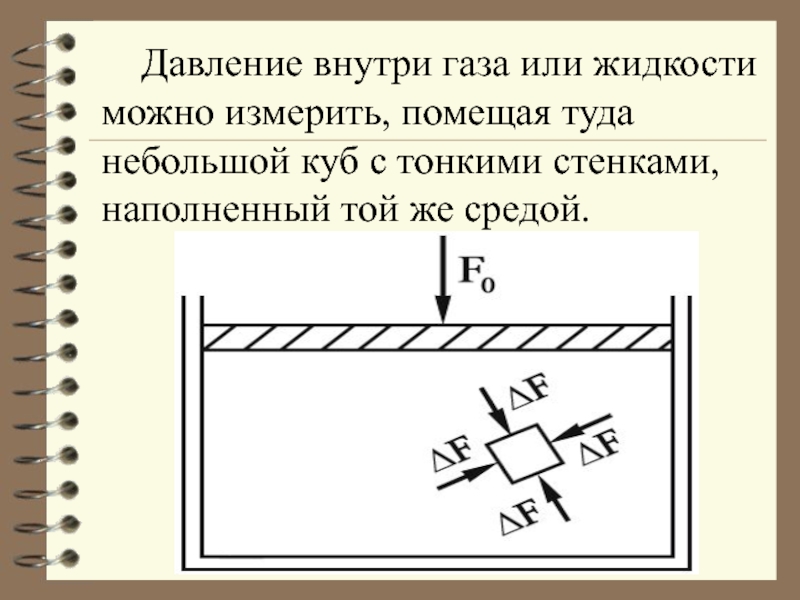
- 15. Давление внутри газа или жидкости можно измерить,
- 16. Поскольку среда покоится, на каждую грань куба
- 17. Внутреннее давление является
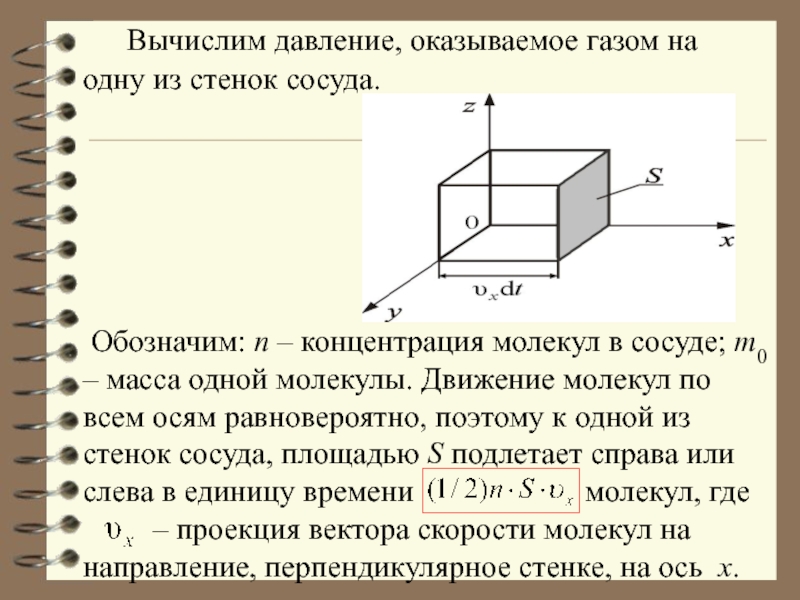
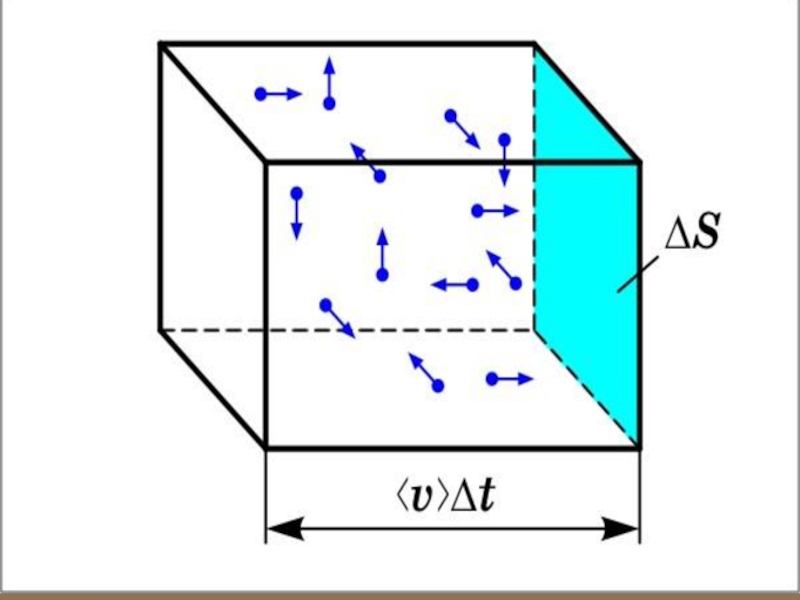
- 18. Вычислим давление, оказываемое газом
- 20. Каждая молекула обладает импульсом m0υx, но стенка
- 21. Наивно полагать, что все молекулы
- 22. Под скоростью
- 23. Следовательно, на другие стенки будет точно такое
- 25. Единицы измерения давления. По определению,
- 26. Чтобы связать энергию с температурой, Больцман ввел
- 27. Величину T называют абсолютной температурой и измеряют
- 28. Тогдa для NA частиц идеального газа:
- 29. Основное уравнение молекулярно-кинетической теории можно записать
- 30. Из уравнения
- 31. Основные законы идеального газа
- 32. 1.Изохорический процесс. V = const. Изохорическим
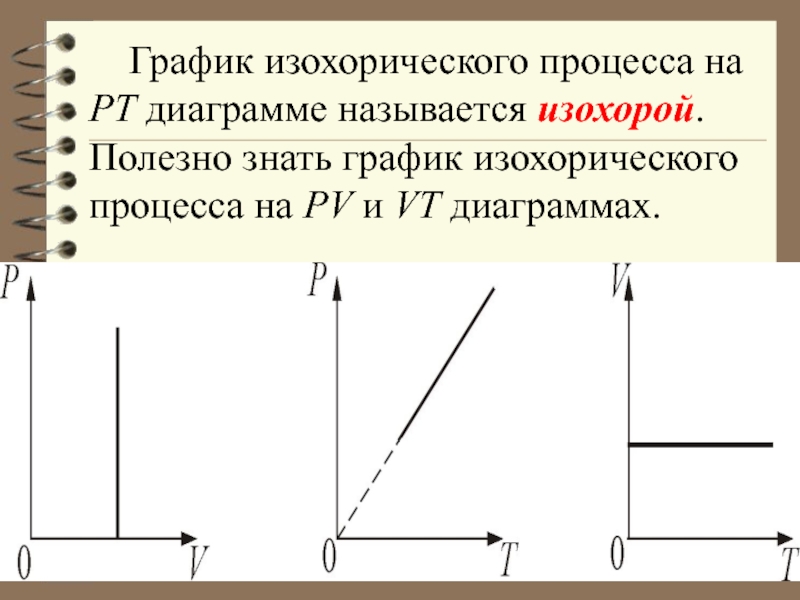
- 33. График изохорического процесса на РТ диаграмме называется
- 34. 2. Изобарический процесс. Р = const.
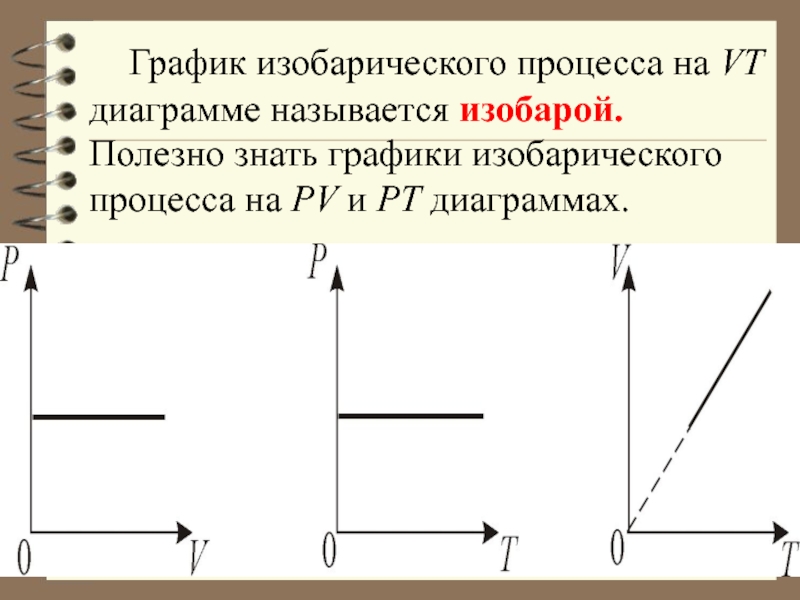
- 35. График изобарического процесса на VT диаграмме называется
- 36. 3. Изотермический процесс. T = const.
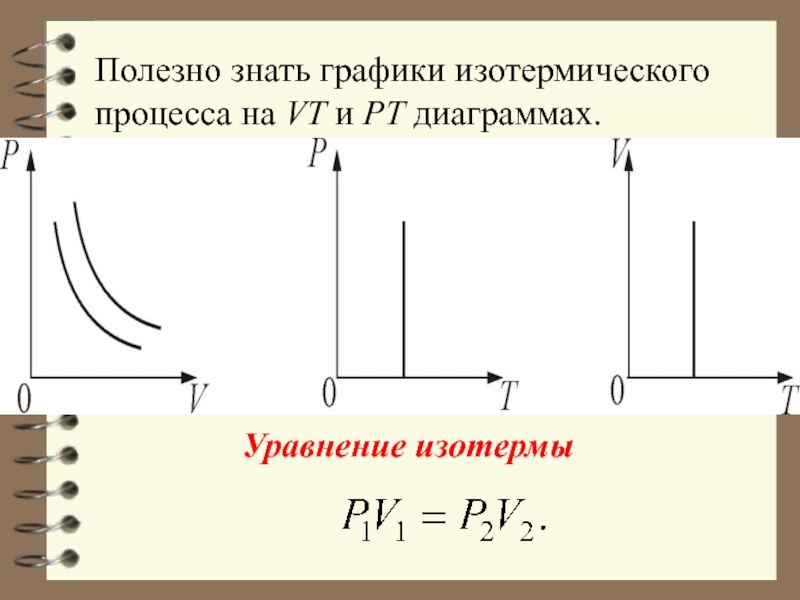
- 37. Полезно знать графики изотермического процесса на VT
- 38. 4. Адиабатический процесс (изоэнтропийный). Процесс, происходящий
- 39. 6. Закон Авогадро. При одинаковых давлениях
- 40. 7. Закон Дальтона. Давление смеси идеальных
- 41. 8. Объединённый газовый закон (Закон Клапейрона).
- 42. Менделеев объединил известные нам законы Бойля-Мариотта, Гей-Люссака
- 43. Если обозначим
- 44. Согласно закону Дальтона: полное давление смеси
Слайд 2Лекция № 1
1. Состояние термодинамического равно-
весия. Температура.
2. Модель
3. Уравнение Клапейрона-Менделеева. Основные законы идеального газа.
Слайд 3 СТАТИСТИЧЕСКИЙ И ТЕРМО- ДИНАМИЧЕСКИЙ МЕТОДЫ
Существуют два способа описания
дящих в макроскопических телах (телах, состоящих из
большого числа частиц) – статистический и термодина-
мический. Статистический метод изучает свойства макро-
скопических тел исходя из свойств образующих тело
частиц и взаимодействий между ними. Свойства тел,
наблюдаемые на опыте, объясняются как усредненный
результат действия отдельных молекул. Термодинамический метод изучает свойства тел, не
вдаваясь в их микроскопическую структуру, а опираясь на
фундаментальные законы ( начала термодинамики),
установленные обобщением экспериментальных фактов.
Слайд 5ТЕРМОДИНАМИЧЕСКАЯ СИСТЕМА. ПАРАМЕТРЫ СОСТОЯНИЯ
Термодинамической системой называется совокупность
макроскопических тел,
гией между собой и окружающей средой.
Термодинамическая система может находиться в различ-
ных состояниях, различающихся температурой, давлением,
объемом, плотностью… Подобные величины, характери-
зующие состояние системы,
называются параметрами
состояниями. Термодинами-
ческие системы, которые не
обмениваются с внешней сред-
ой ни энергией, ни веществом
называются замкнутыми
(изолированными).
Слайд 6 РАВНОВЕСНЫЕ И
НЕРАВНОВЕСНЫЕ СОСТОЯНИЯ
Параметры состояния не всегда име-
ют определенные значения (одина-
ковые
Состояние, в котором хотя бы один
из параметров не имеет определен-
ного значения, называется неравно-
весным.
Состояние термодинамической сис-
темы будет равновесным, если все
параметры cостояния имеют опре-
деленные значения, не изменяющие-
ся с течением времени.
Слайд 7 РАВНОВЕСНЫЕ ПРОЦЕССЫ
Термодинамическим процессом называется переход системы из
одного состояния в другое.
шением равновесия системы. Например,
при сжатии газа давление в первую оче-
редь возрастет вблизи поршня – равнове-
сие нарушится. Нарушение равновесия
будет тем значительнее, чем быстрее пере-
мещать поршень. Если двигать поршень
очень медленно, то равновесие нарушает-
ся незначительно и давление в разных точ-
ках мало отличается от равновесного для
данного объема газа. В пределе, при беско-
нечно медленном сжатии процесс окажется состоящим
из последовательности равновесных состоя-
ний. Процесс называется равновесным или квазистатическим.
Слайд 8 Состояние термодинамической системы, не изменяющееся во времени и не сопровожда-ющееся
Параметры состояния при термодинамическом равновесии можно считать постоянными.
Изолированная система со временем всегда
приходит к равновесному состоянию и не может самопроизвольно из него выйти.
Данное утверждение часто называю нулевым началом термодинамики.
Слайд 9ТЕМПЕРАТУРА
Если два тела находятся в состоянии термодина-
мического равновесия, то
энергией путем теплопередачи, то этим телам
приписывается одинаковая температура.
Температура – физическая величина, характе-
ризующая степень нагретости тел и определяет
направление передачи тепла.
Если между телами происходит направленный
теплообмен, то телу отдающему энергию припи-
сывают большую температуру по сравнению с
телом, получающим тепловую энергию.
Слайд 10 В физике и технике за абсолютную шкалу температур принята шкала Кельвина,
Слайд 11 Абсолютная температура Т не может быть отрицательной величиной. Своеобразие температуры
Слайд 12 Модель
Абстрактная модель, отражающая существенные черты явления, аналогичная материальной точке.
1. Молекулы (или атомы) газа не имеют собственного объема, то есть рассматриваются как материальные точки.
2. Силы взаимодействия между атомами и молекулами идеального газа пренебрежимо малы. Поэтому потенциальной энергией взаимодействия можно пренебречь. Отсюда, внутренняя энергия идеального газа – сумма кинетических энергий хаотического движения всех молекул. Взаимодействие же молекул сводится к упругим столкновениям.
Справедливо для газов в разреженном состоянии. Отсюда – идеальный газ: система невзаимодействующих материальных точек.
Слайд 13 Давление. Основное уравнение молекулярно-кинетической теории
Ещё в XVIII веке Даниил Бернулли предположил, что давление газа – есть следствие столкновения газовых молекул со стенками сосуда.
Именно давление чаще всего является единственным сигналом присутствия газа.
Слайд 14 Находящиеся под давлением газ или жидкость действуют
Слайд 15 Давление внутри газа или жидкости можно измерить, помещая туда небольшой куб
Слайд 16 Поскольку среда покоится, на каждую грань куба со стороны среды действует
Слайд 17 Внутреннее давление является одним и тем же
Слайд 18 Вычислим давление, оказываемое газом на одну из стенок
Слайд 20Каждая молекула обладает импульсом m0υx, но стенка получает импульс
Слайд 21 Наивно полагать, что все молекулы подлетают к стенке S
Более точно случайную величину характеризует среднеквадра-тичная величина.
Слайд 22 Под скоростью понимаем среднеквадратичную скорость
Слайд 23 Следовательно, на другие стенки будет точно такое же давление. Тогда можно
Слайд 25 Единицы измерения давления. По определению,
Слайд 26 Чтобы связать энергию с температурой, Больцман ввел коэффициент пропорциональ-ности k, который
Слайд 27 Величину T называют абсолютной температурой и измеряют в градусах Кельвина (К).
Слайд 28Тогдa для NA частиц идеального газа: следовательно,
Слайд 29 Основное уравнение молекулярно-кинетической теории можно записать по другом Т.к. Отсюда: В таком
Слайд 30
Из уравнения
объёме V содержится N частиц и концен-
трация их n = N/V , получим:
Если ввести величину - число молей,
то и получаем:
- уравнение Клапей-
рона-Менделеева
Слайд 31 Основные законы идеального газа
В XVII – XIX веках
Изопроцессы идеального газа – процессы, при которых один из параметров остаётся неизменным.
Слайд 32 1.Изохорический процесс. V = const. Изохорическим процессом называется процесс, протекающий при
Слайд 33 График изохорического процесса на РТ диаграмме называется изохорой. Полезно знать график
Слайд 34 2. Изобарический процесс. Р = const. Изобарическим процессом называется процесс,
Слайд 35 График изобарического процесса на VT диаграмме называется изобарой. Полезно знать графики
Слайд 36 3. Изотермический процесс. T = const. Изотермическим процессом называется процесс, протекающий
Слайд 384. Адиабатический процесс (изоэнтропийный). Процесс, происходящий без теплообмена с окружающей средой. 5.
Слайд 396. Закон Авогадро.
При одинаковых давлениях и одинаковых температурах, в равных
В одном моле различных веществ содержится молекул (число Авогадро).
Слайд 407. Закон Дальтона. Давление смеси идеальных газов равно сумме парциальных давлений
Слайд 418. Объединённый газовый закон (Закон Клапейрона). В соответствии с законами Бойля
Слайд 42 Менделеев объединил известные нам законы Бойля-Мариотта, Гей-Люссака и Шарля с законом
Слайд 43Если обозначим – плотность
Слайд 44 Согласно закону Дальтона: полное давление смеси газа равно сумме парциальных