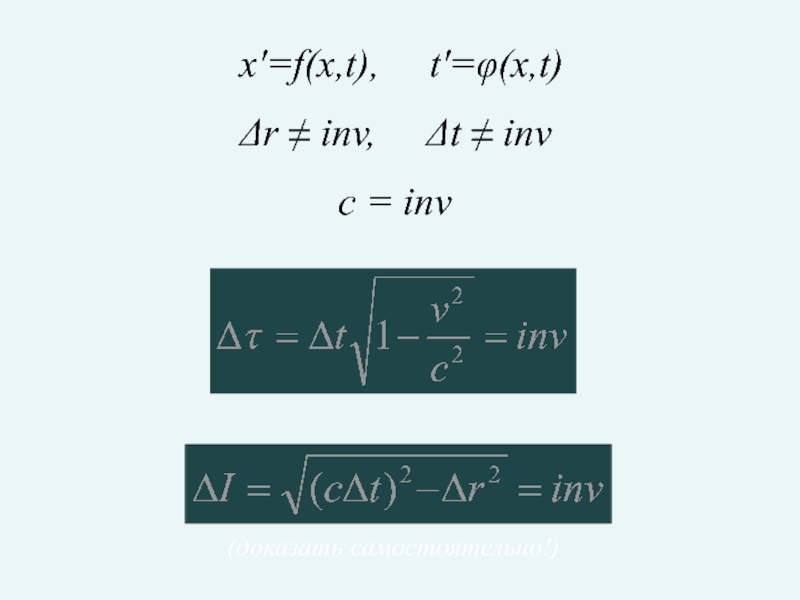- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Spetsialnaya_teoria_otnositelnosti_STO презентация
Содержание
- 1. Spetsialnaya_teoria_otnositelnosti_STO
- 2. Постулаты Эйнштейна (1905 г.) Принцип относительности: все
- 3. Принцип существования предельной скорости материальных объектов
- 4. Понятно, что одновременно удовлетворять принципам относительности Эйнштейна
- 5. Преобразования Лоренца Получим преобразования Лоренца, опираясь на
- 6. Преобразования Лоренца Пусть в момент
- 7. Преобразования Лоренца Подставив значение из
- 8. Преобразования Лоренца Подставив значение
- 9. Преобразования Лоренца y z x к {x',y',z'}
- 10. Относительность одновременности y z x к
- 11. Пространство и время в движущихся ИСО Следствия
- 12. x z y z' x' y' x'1
- 13. x z y z' x' y' x'1 x'2 к к' l' l=? !
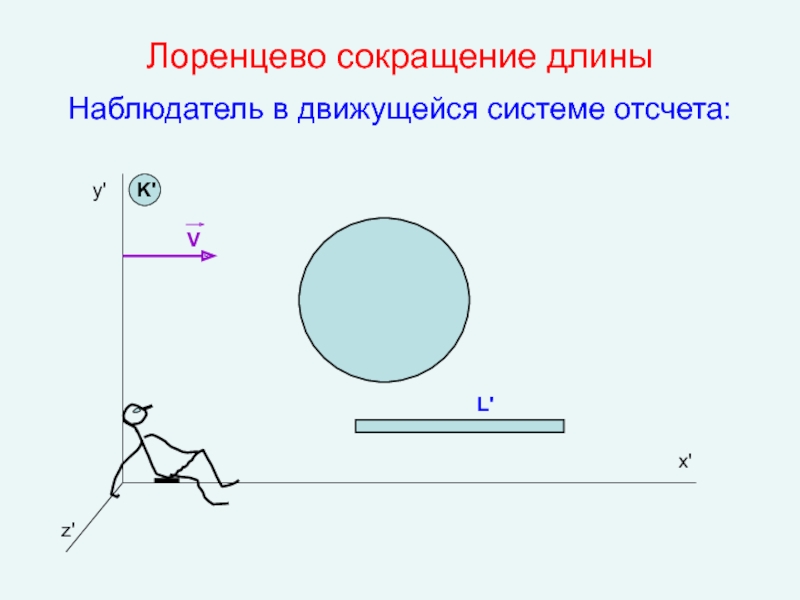
- 14. Лоренцево сокращение длины Наблюдатель в движущейся
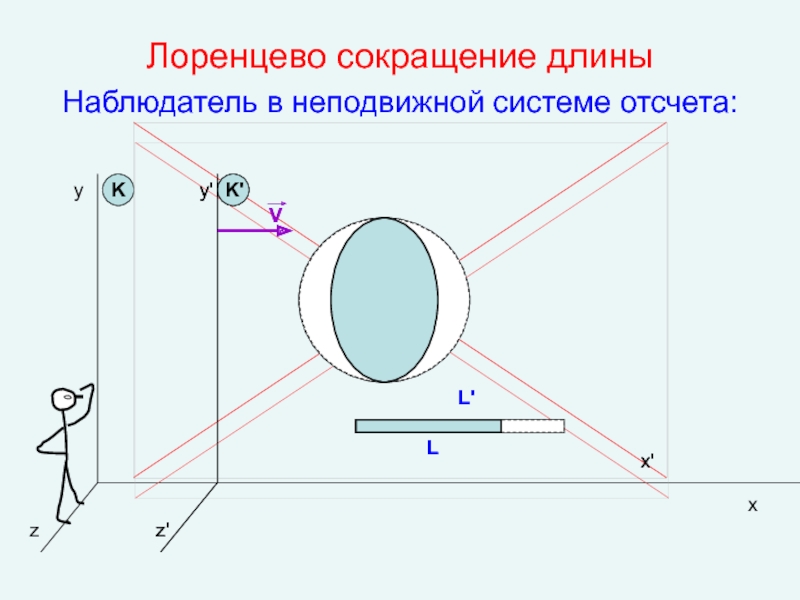
- 15. Лоренцево сокращение длины Наблюдатель в неподвижной
- 16. Лоренцево сокращение длины
- 17. Пространство и время в движущихся ИСО Следствия
- 18. z y z' y' к к' Преобразования
- 19. Пространство и время в движущихся ИСО Следствия
- 20. x z y к Δt=? Преобразование Лоренца
- 21. Для наблюдателя, находящегося в
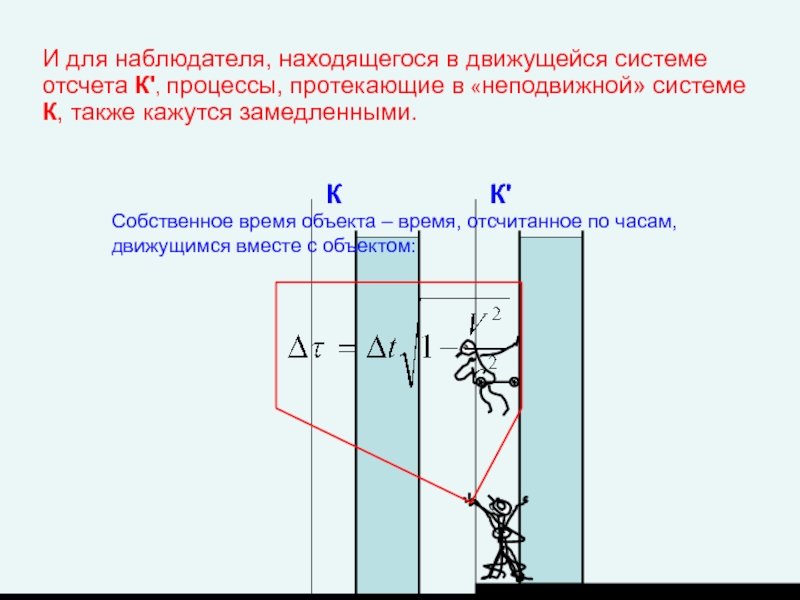
- 22. И для наблюдателя, находящегося в
- 23. Пространство и время в движущихся ИСО Единое
- 25. Следствия из преобразований Лоренца: Закон сложения скоростей
- 26. Энергия и импульс Релятивистская энергия и релятивистский
- 27. Связь между релятивистским импульсом и энергией После
- 28. Кинетическая энергия Кинетическая энергия релятивистской частицы определяется
- 29. Уравнение динамики Основное уравнение динамики
Слайд 2Постулаты Эйнштейна (1905 г.)
Принцип относительности: все законы природы инвариантны по отношению
Принцип постоянства скорости света: скорость света в вакууме не зависит от скорости движения источника света или наблюдателя и одинакова во всех инерциальных системах отсчета.
Эйнштейн Альберт 1879 – 1955
Слайд 3Принцип существования предельной скорости материальных объектов
Фундаментальный закон природы:
Слайд 4Понятно, что одновременно удовлетворять принципам относительности Эйнштейна и принципу постоянства скорости
Но этим условиям удовлетворяют преобразования Лоренца, с которых начинается специальная теория относительности и из которых вытекает ряд необычных с точки зрения ньютоновской механики следствий.
Слайд 5Преобразования Лоренца
Получим преобразования Лоренца, опираясь на
постулаты Эйнштейна.
Учитывая однородность пространства и
можно предположим, что новые преобразования
линейны, тогда
По принципу относительности все инерциальные
системы отсчета равноправны, следовательно,
можно записать
Слайд 6Преобразования Лоренца
Пусть в момент ,
Следовательно,
Слайд 8Преобразования Лоренца
Подставив значение в одну
или
и решив полученное уравнение относительно t,
получим
Слайд 10Относительность одновременности
y
z
x
к
Пусть в системе
к'
но
Покажем, что в системе
к
Доказательство:
или
Слайд 11Пространство и время в движущихся ИСО
Следствия из преобразований
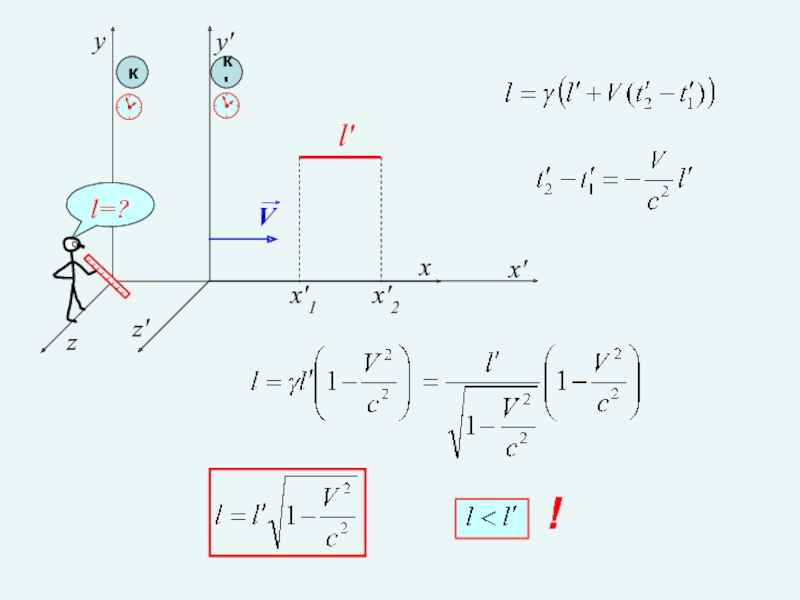
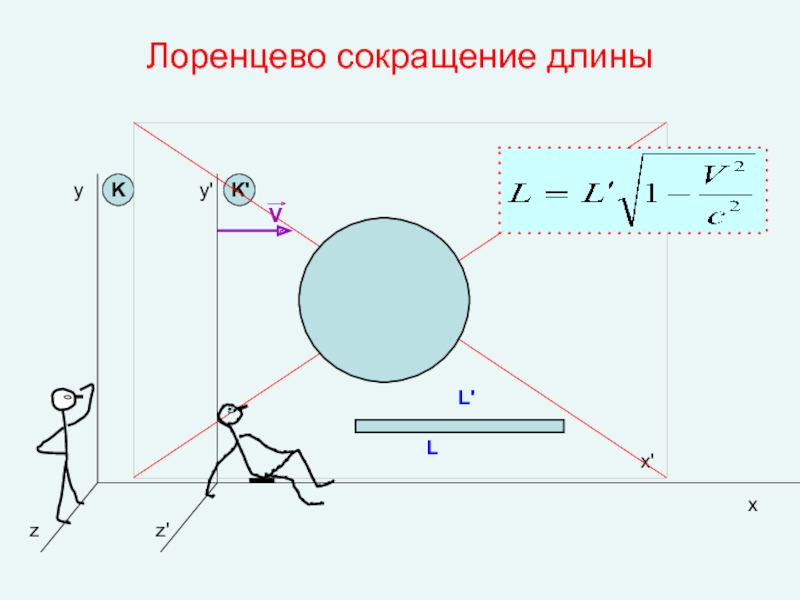
Лоренцево сокращение длины
Слайд 12x
z
y
z'
x'
y'
x'1
x'2
к
к'
l'
l=?
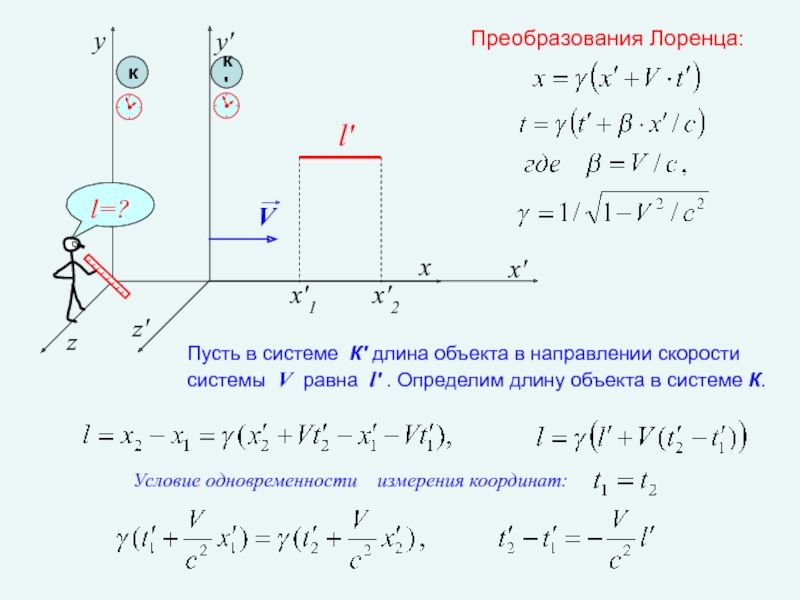
Условие одновременности измерения координат:
Преобразования Лоренца:
Пусть в системе К' длина объекта
Слайд 17Пространство и время в движущихся ИСО
Следствия из преобразований
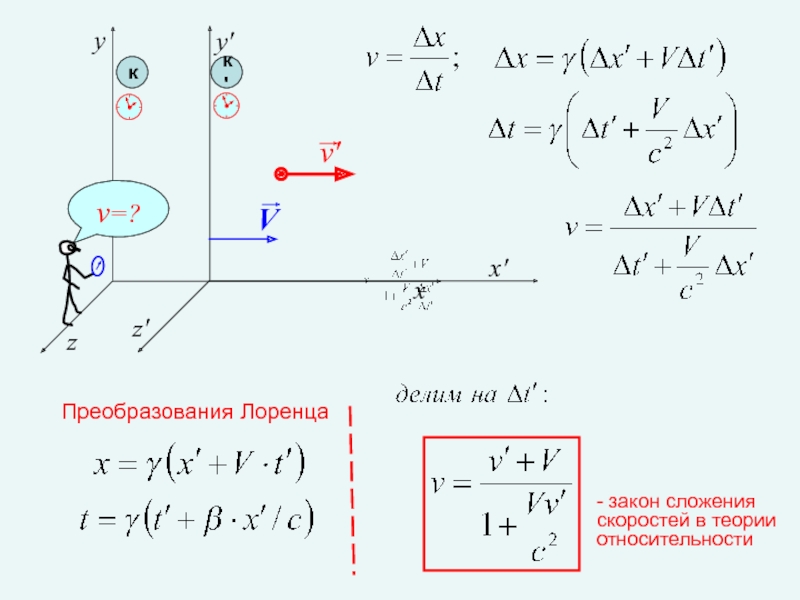
Закон сложения скоростей
в теории относительности
Слайд 19Пространство и время в движущихся ИСО
Следствия из преобразований
Лоренцево замедление
Собственное время жизни объекта
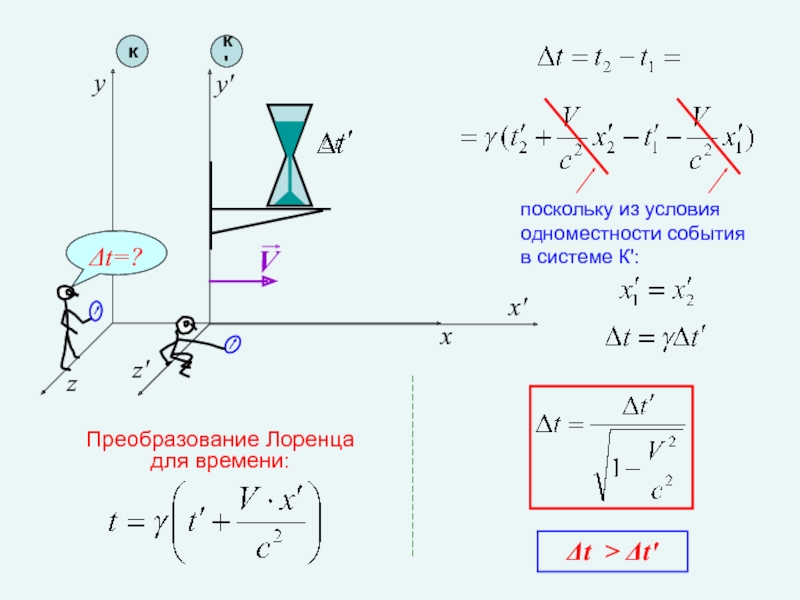
Слайд 20x
z
y
к
Δt=?
Преобразование Лоренца для времени:
поскольку из условия одноместности события
в системе К':
Δt
Слайд 21
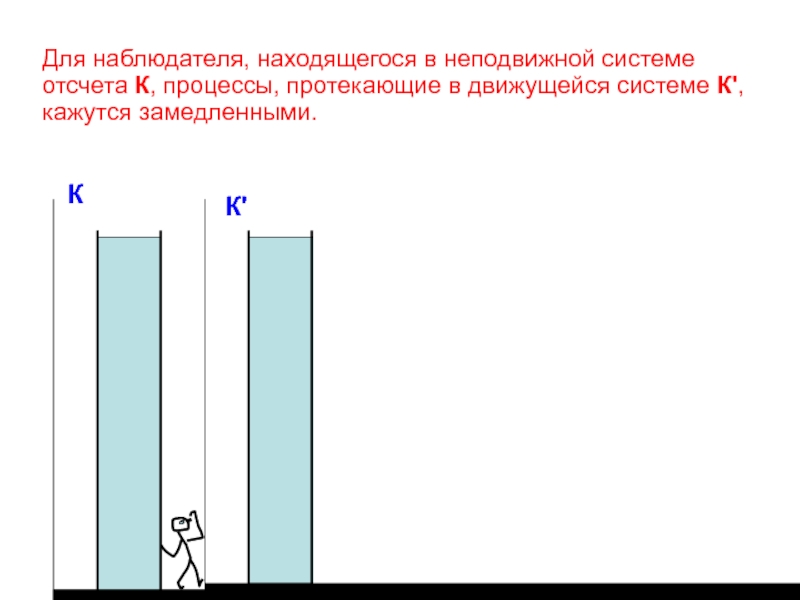
Для наблюдателя, находящегося в неподвижной системе отсчета К, процессы, протекающие в
К
К'
Слайд 22
И для наблюдателя, находящегося в движущейся системе отсчета К', процессы, протекающие
К'
Собственное время объекта – время, отсчитанное по часам, движущимся вместе с объектом:
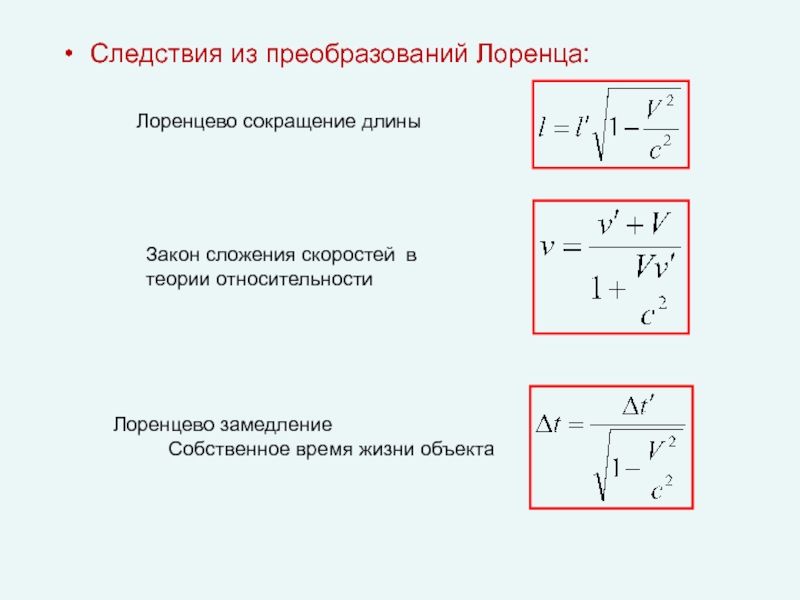
Слайд 25Следствия из преобразований Лоренца:
Закон сложения скоростей в теории относительности
Лоренцево сокращение длины
Лоренцево
Собственное время жизни объекта
Слайд 26Энергия и импульс
Релятивистская энергия и релятивистский импульс будут определяться следующими выражениями:
Закон
-энергия покоя
-энергия движения
Слайд 27Связь между релятивистским импульсом и энергией
После преобразований получим
Можно записать еще одну
Запишем выражения для импульса и энергии и исключим из них скорость