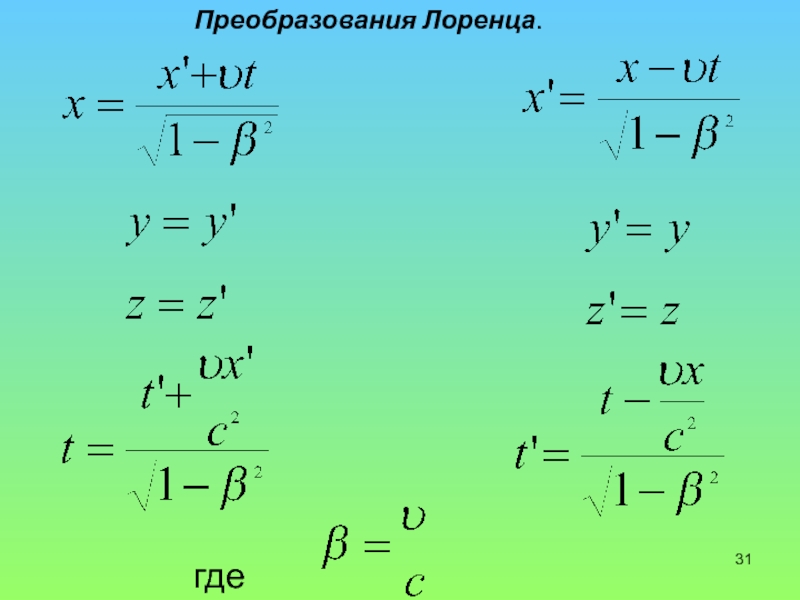- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Специальная теория относительности презентация
Содержание
- 1. Специальная теория относительности
- 2. 1. Принцип относительности Галилея.
- 3. Механика Ньютона оказалась замечатель-ным приближением к релятивистской
- 4. Рассмотрим две инерциальные системы отсчета k и
- 5. Найдем связь между координатами точки M в
- 6. В уравнениях (8.1.1)
- 7. Продифференцируем это выражение по
- 8. Преобразования Галилея Таким образом видим, что для
- 9. Законы природы, определяющие изменение состояния
- 10. Из преобразований Галилея и принципа относительности следует,
- 11. В 1865 г. появилась теория Дж. Максвелла,
- 12. В теории Максвелла, скорость света (скорость распространения
- 13. Нужна была экспериментальная проверка теории Максвелла. Он
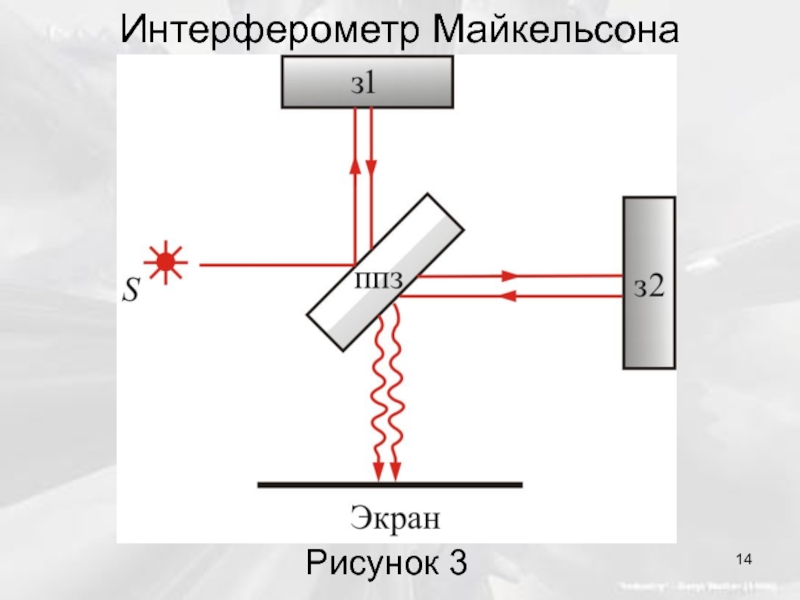
- 14. Интерферометр Майкельсона Рисунок 3
- 15. Вследствие сравнительно большой скорости движения
- 16. В результате, световые волны, пройдя указанные пути,
- 17. Эти опыты повторяли и перепроверяли многократно. В
- 18. Эта точность в 3 раза выше достигнутой
- 19. Было много попыток объяснить отрицательный результат опыта
- 20. Х.Лоренц Г. Минковский А.Эйнштейн
- 21. 2. Принцип относительности Эйнштейна В 1905 г.
- 22. Принцип относительности Эйнштейна представляет собой фундаментальный физический
- 23. Инвариантность – неизменность вида уравнения при
- 24. В первом постулате главное, что время тоже
- 25. 3. Преобразования Лоренца Формулы преобразования при переходе
- 26. Его работы посвящены
- 27. Рассмотрим две инерциальные системы отсчета (неподвижную и
- 28. Как связаны между собой эти координаты и
- 29. Лоренц установил
- 30. - все инерциальные системы отсчета физически эквивалентны;
- 31. где Преобразования Лоренца.
- 32. Истинный физический смысл преобразований Лоренца был
- 33. Полученные уравнения связывают координаты и время в
- 34. 4. Следствия из преобразований Лоренца 1. Одновременность
- 35. Рисунок 8.4 Если свет встретится на середине
- 36. Рассмотрим это более подробно. Пусть в системе
- 37. В соответствии с преобразованиями Лоренца для
- 38. События будут абсолютно одновременны в системах
- 39. (4.5) Разница во времени будет
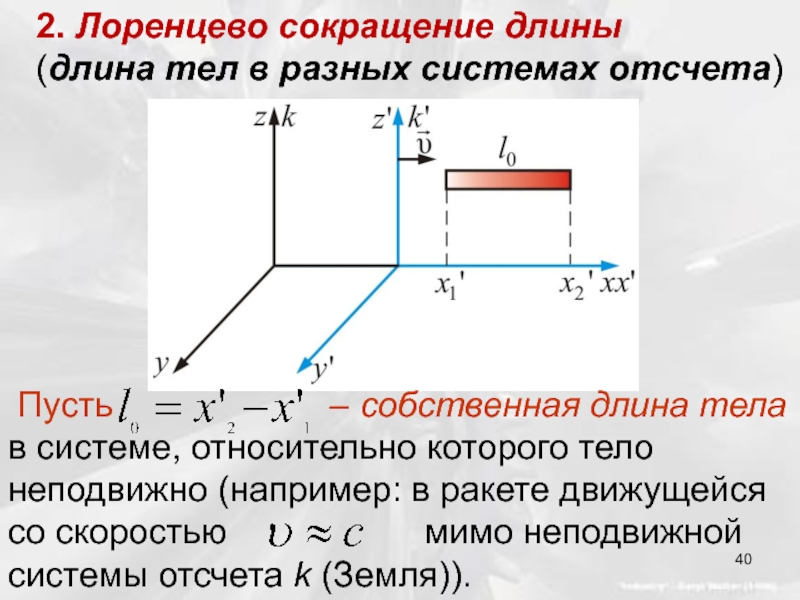
- 40. 2. Лоренцево сокращение длины (длина тел
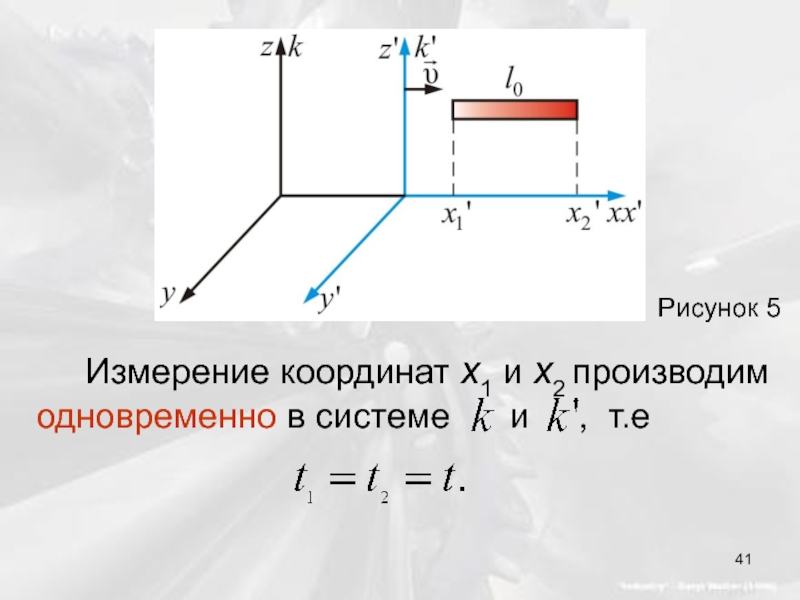
- 41. Рисунок 5
- 42. Используя преобразования Лоренца, для координат получим: т.е. или (4.6)
- 43. Формула называется Лоренцевым
- 44. 3. Замедление времени (длительность событий в разных
- 45. или (4.7) Из
- 47. Так, нестабильные элементарные частицы – пионы, рождающиеся
- 48. В 60 – 70 гг. замедление времени
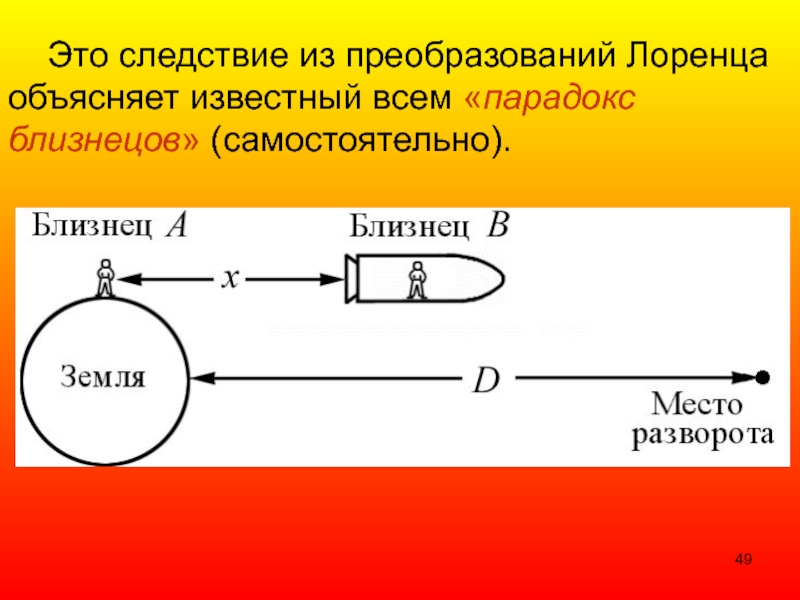
- 49. Это следствие из преобразований Лоренца объясняет известный всем «парадокс близнецов» (самостоятельно).
- 50. 4. Парадокс близнецов
- 51. Рис. 7.7
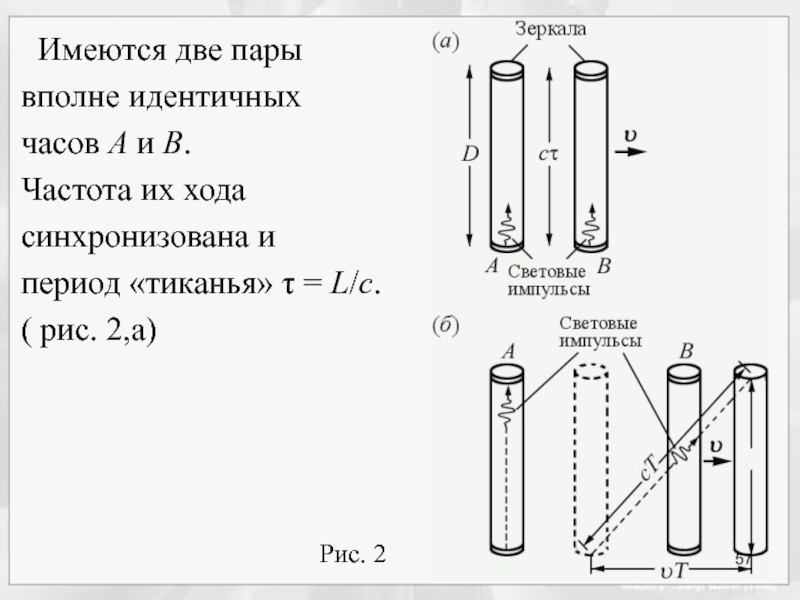
- 57. Рис. 2
- 58. 4. Сложение скоростей в релятивистской механике
- 59. Классическая механика ответит на этот вопрос просто:
- 60. Оценим скорость тела, используя преобразования Лоренца. Внутри
- 61. Так как
- 62. Подсчитаем скорость тела в нашем примере в
- 63. При медленных движениях, когда получаем нерелятивистские
- 64. Полученные формулы сложения скоростей запрещают движение со
- 65. 5. Релятивистская механика
- 66. Ньютоновское выражение для импульса
- 67. (5.2) Это и есть
- 69. Релятивистское выражение для
- 70. После интегрирования этого выражения получим релятивистское
- 72. Именно утверждение о том, что в покоящейся
- 73. Справедливость теории проверяется принципом
- 74. Получим еще одно очень важное соотношение, связывающее
- 75. 6. Взаимосвязь массы и энергии покоя Масса
- 76. Взаимосвязь между массой и энергией оценивалась А.
- 77. Эйнштейна
- 78. Пример: пусть две одинаковые по массе частицы
- 79. откуда М равно: (6.2)
- 80. (это при отсутствии выделения энергии при
- 81. Энергия связи – энергия которую нужно затратить,
- 82. Это и наблюдается на
- 83. Ядерные реакции Ядерной реакцией называется процесс взаимодействия
- 84. В ядерной энергетике большой практический интерес
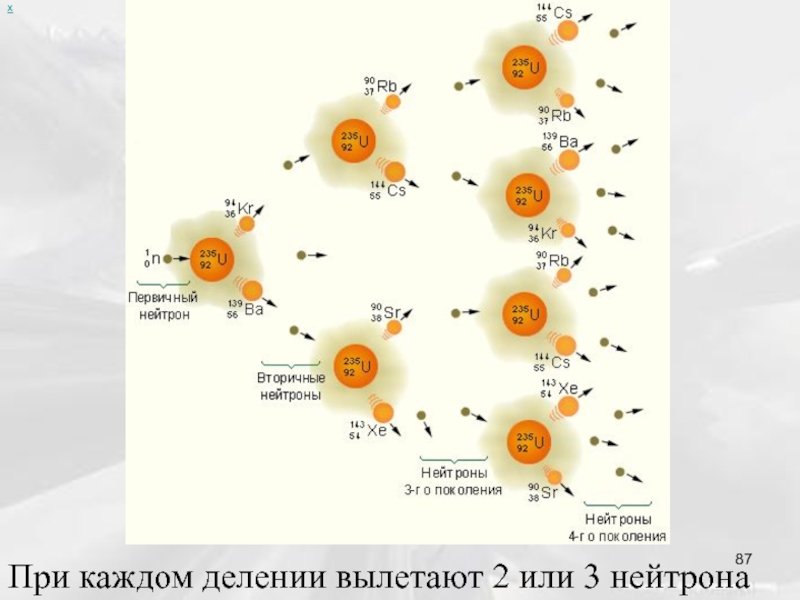
- 85. Характерно, что в каждом акте деления возникает
- 86. х В процессе деления ядро изменяет форму
- 87. х При каждом делении вылетают 2 или 3 нейтрона
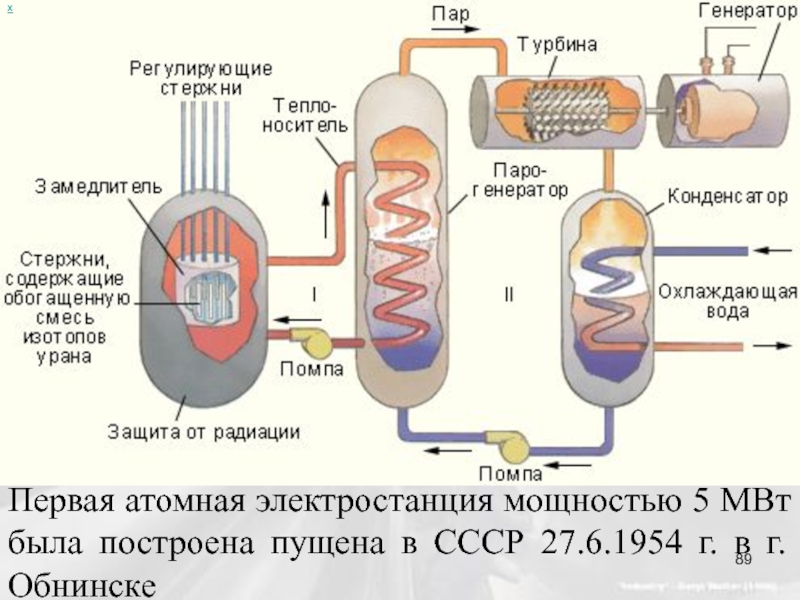
- 88. Его основные элементы: ядерное топливо, замедлитель
- 89. х Первая атомная электростанция мощностью 5 МВт
- 90. документальная фотография А. М. Антонова, ТЭФ
- 91. Конструктивная схема реактора на быстрых нейтронах типа
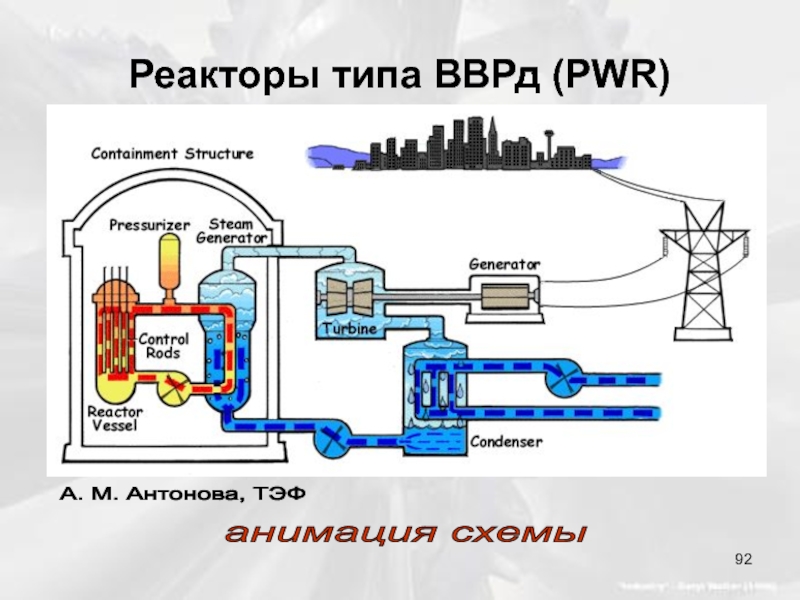
- 92. Реакторы типа ВВРд (PWR) анимация схемы А. М. Антонова, ТЭФ
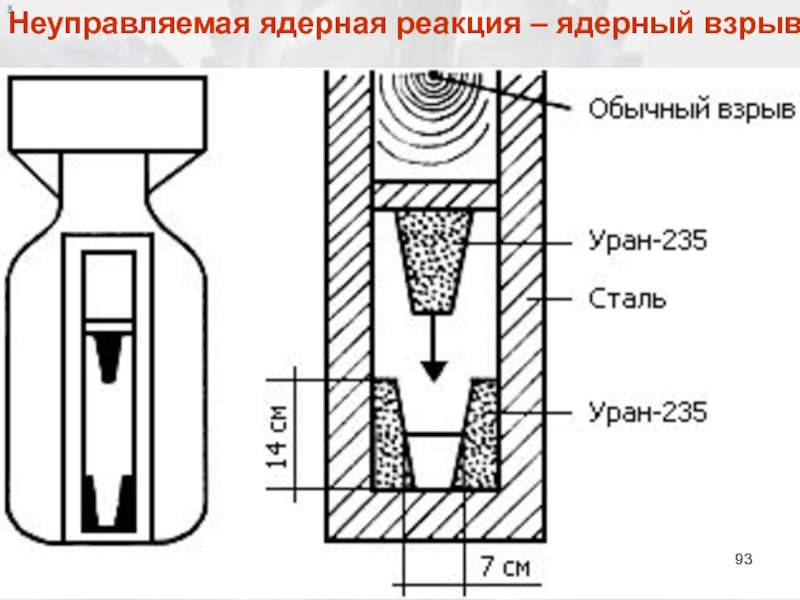
- 93. х Неуправляемая ядерная реакция – ядерный взрыв
- 94. Термоядерные реакции Термоядерные реакции – это
- 95. Энергия, выделяющаяся в процессе термоядерных реакций в
- 96. наиболее перспективна в плане получения практически
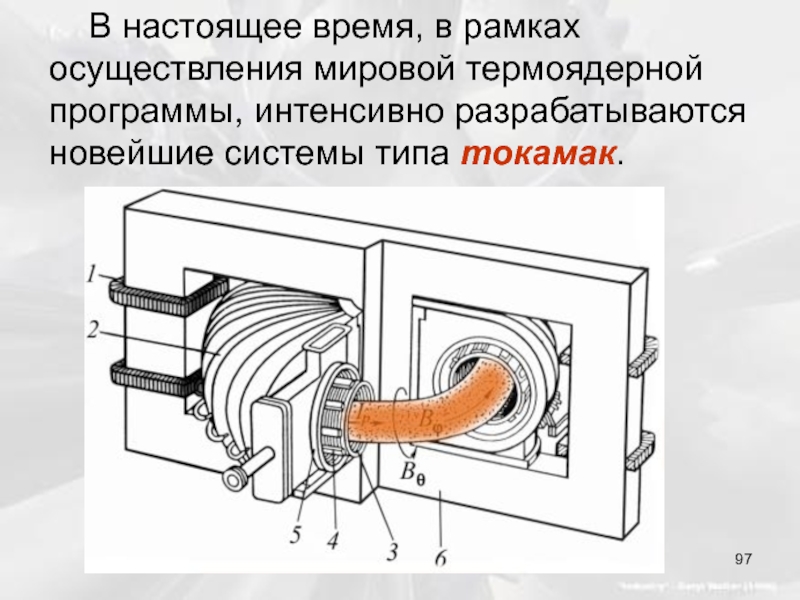
- 97. В настоящее время, в рамках осуществления мировой термоядерной программы, интенсивно разрабатываются новейшие системы типа токамак.
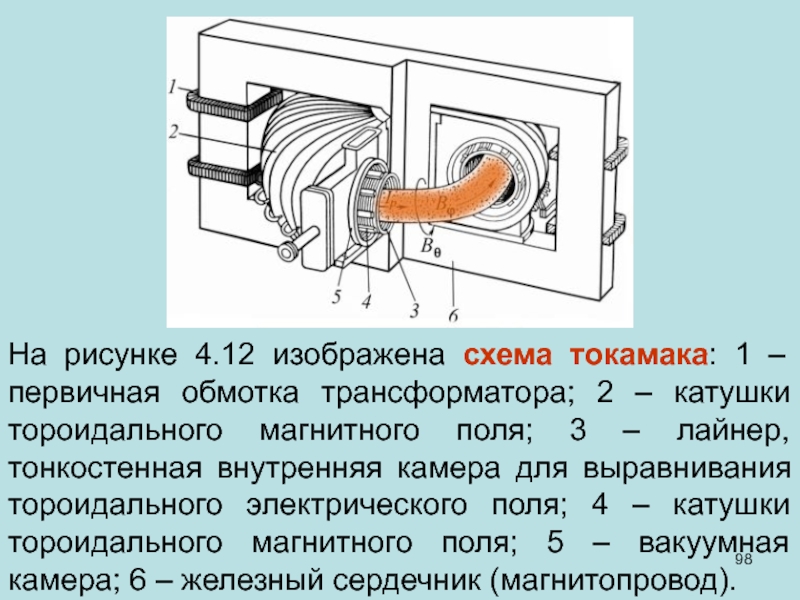
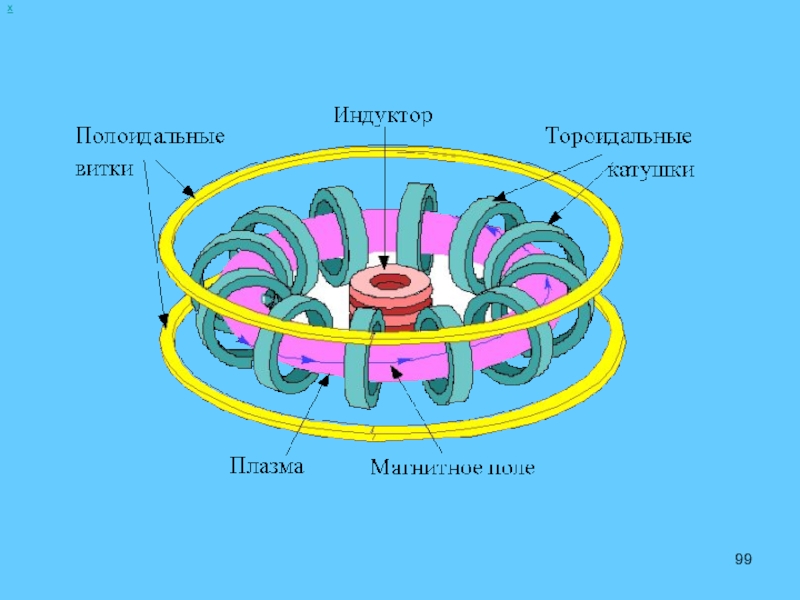
- 98. На рисунке 4.12 изображена схема токамака: 1
- 99. х
- 100. Есть надежда, что термоядерный реактор практического
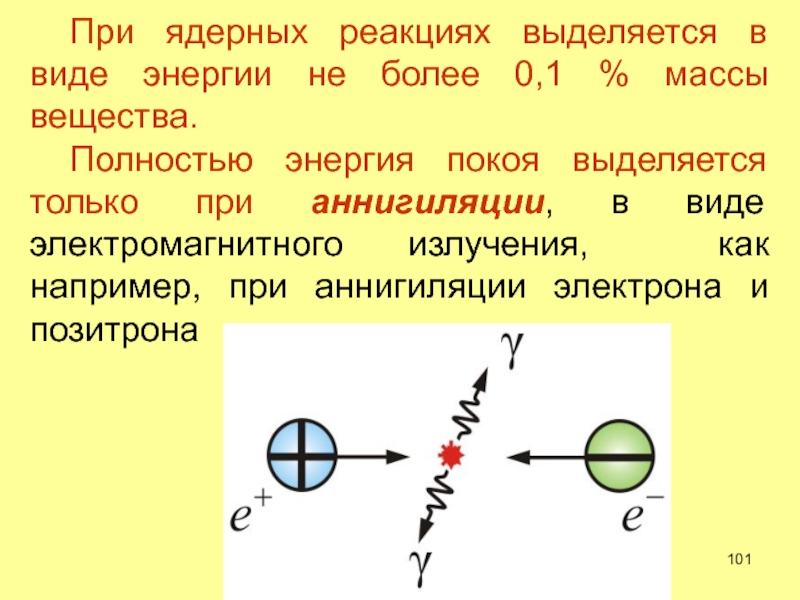
- 101. При ядерных реакциях выделяется в
Слайд 1
СПЕЦИАЛЬНАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ (СТО)
1. Принцип относительности Галилея. Закон сложения скоростей
2.
3. Преобразования Лоренца
4. Следствия из преобразований Лоренца
5. Релятивистская механика
6. Взаимосвязь массы и энергии покоя
Слайд 3Механика Ньютона оказалась замечатель-ным приближением к релятивистской механике, справедливым в области
Большинство встречающихся в повседневной жизни скоростей значительно меньше скорости света. Но существуют явления, где это не так (ядерная физика, электромагнетизм, фотоэффект, астрономия ).
По классической механике: механические явления происходят одинаково в двух системах отсчета, движущихся равномерно и прямолинейно относительно друг друга.
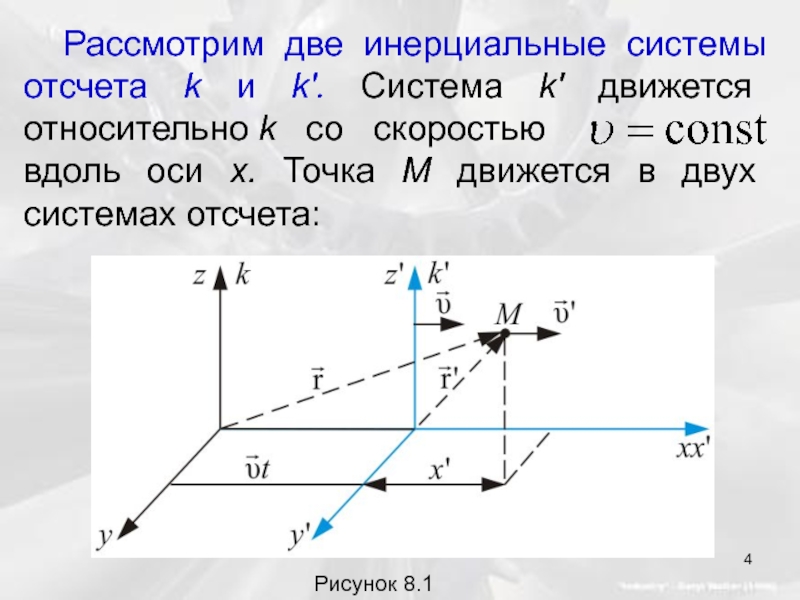
Слайд 4 Рассмотрим две инерциальные системы отсчета k и k'. Система k' движется
вдоль оси x. Точка М движется в двух системах отсчета:
Рисунок 8.1
Слайд 5 Найдем связь между координатами точки M в обеих системах отсчета. Отсчет
(1.1)
Это т.н. преобразования Галилея.
Слайд 6
В уравнениях (8.1.1) время
В векторной форме преобразования Галилея можно записать так:
(1.2)
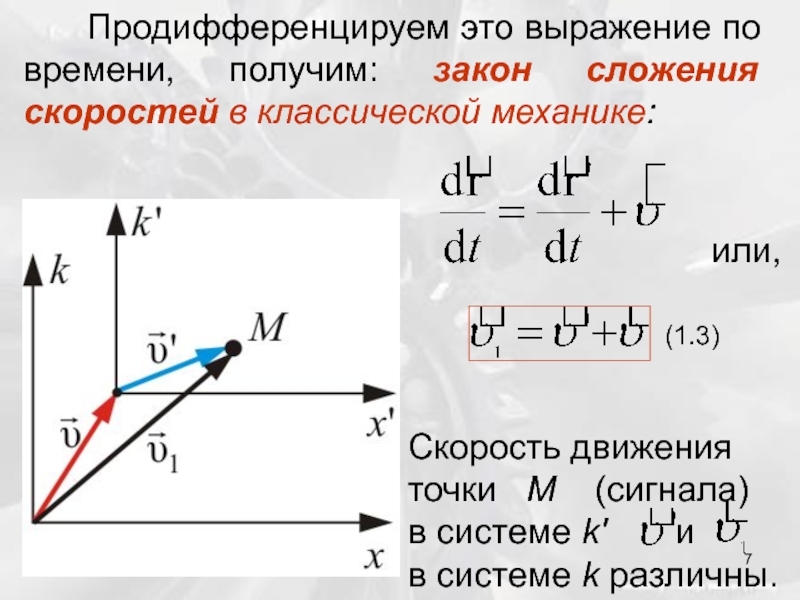
Слайд 7 Продифференцируем это выражение по времени, получим: закон сложения
или,
(1.3)
Скорость движения точки М (сигнала)
в системе k' и в системе k различны.
Слайд 8Преобразования Галилея
Таким образом видим, что для однозначного определения кинематических параметров, описывающих
В классической механике проблема взаимосвязи моментов времени в различных СО решается постулатом Галилея
Моменты времени в различных СО
совпадают
с точность до постоянной величины,
определяемой процедурой синхронизации часов
Обычно считают часы синхронизированными таким образом, что const = 0, то есть
При таком способе синхронизации
Из последнего уравнения несложно получить связь ускорений в произвольных СО
где ao - ускорение системы K0 относительно системы K
Эти уравнения называют преобразованиями Галилея для произвольных СО
Слайд 9
Законы природы, определяющие изменение состояния движения механических систем не зависят от
Это принцип относительности Галилея.
Слайд 10 Из преобразований Галилея и принципа относительности следует, что взаимодействия в классической
Принцип относительности Галилея и законы Ньютона подтверждались ежечасно при рассмотрении любого движения, и господствовали в физике более 200 лет.
Слайд 11 В 1865 г. появилась теория Дж. Максвелла, и уравнения Максвелла не
Слайд 12 В теории Максвелла, скорость света (скорость распространения электромагнит-ных волн), конечна
А в теории Галилея скорость передачи сигнала бесконечна и зависит от системы отсчета
Первые догадки о конечности распространения скорости света, были высказаны еще Галилеем. Астроном Рёмер в 1676 г. пытался найти скорость света. По его приближенным расчетам, она была равна
Слайд 13 Нужна была экспериментальная проверка теории Максвелла. Он сам предложил идею опыта
В 1881г. были выполнены опыты, которые доказали независимость скорости света от скорости источника или наблюдателя.
Необходимый для опыта прибор изобрел блестящий военно-морской офицер США – А. Майкельсон
Слайд 15 Вследствие сравнительно большой скорости движения Земли, свет должен был
Слайд 16 В результате, световые волны, пройдя указанные пути, должны были изменить интерференционную
Точность первых опытов была невелика
Однако, опыт дал отрицательный результат: сдвиг интерференционной картины обнаружить не удалось. Таким образом, результаты опытов Майкельсона - Морли показали, что величина скорости света постоянна и не зависит от движения источника и наблюдателя.
Слайд 17 Эти опыты повторяли и перепроверяли многократно. В конце 60-ых годов Ч.
Независимость скорости света от движения источника и от направления недавно была продемонстрирована с рекордной точностью в экспериментах,
выполненных исследователями из университетов г. Констанц
и г. Дюссельдорф
в которых установлена лучшая на сегодняшний день точность
Слайд 18 Эта точность в 3 раза выше достигнутой ранее. Исследовалась стоячая электромагнитная
Слайд 19 Было много попыток объяснить отрицательный результат опыта Майкельсона-Морли. Наиболее известна гипотеза
Дж. Лармор в 1889 г. доказал, что уравнения Максвелла инвариантны относительно преобразований Лоренца. Очень близок был к созданию теории относительности Анри Пуанкаре. Но Альберт Эйнштейн был первым, кто четко и ясно сформулировал основные идеи теории относительности.
Слайд 212. Принцип относительности Эйнштейна
В 1905 г. в журнале «Анналы физики» вышла
Потом было много статей и книг, поясняющих, разъясняющих, интерпретирующих эту теорию.
Слайд 22 Принцип относительности Эйнштейна представляет собой фундаментальный физический закон, согласно которому любой
Слайд 23
Инвариантность – неизменность вида уравнения при переходе из одной системы отсчета
2. Скорость света в пустоте одинакова во всех инерциальных системах отсчета и не зависит от скорости источника и приемника света.
Все как-то пытались объяснить отрицательный результат опыта Майкельсона-Морли, а Эйнштейн – постулировал это, как закон.
В основе СТО лежат два постулата Эйнштейна
1. Все законы природы одинаковы во всех инерциальных системах отсчета.
Слайд 24 В первом постулате главное, что время тоже относительно – такой же
Второй – возводит отрицательный результат опыта Майкельсона-Морли – в ранг закона природы:
Специальная теория относительности представляет физическую теорию, изучающую пространственно-временные закономерности, справедливые для любых физических процессов, когда можно пренебречь действием тяготения.
Слайд 253. Преобразования Лоренца
Формулы преобразования при переходе из одной инерциальной системы в
Лоренц Хендрик Антон (1853 – 1928) – нидерландский физик-теоретик, создатель классической электронной теории на основе электро-магнитной теории Максвелла-Герца.
Слайд 26 Его работы посвящены термодинамике, электродинамике, статической динамике,
Разработал электродинамику движущихся тел (преобразования Лоренца).
Член многих академий наук, в том числе и АН СССР, лауреат Нобелевской премии.
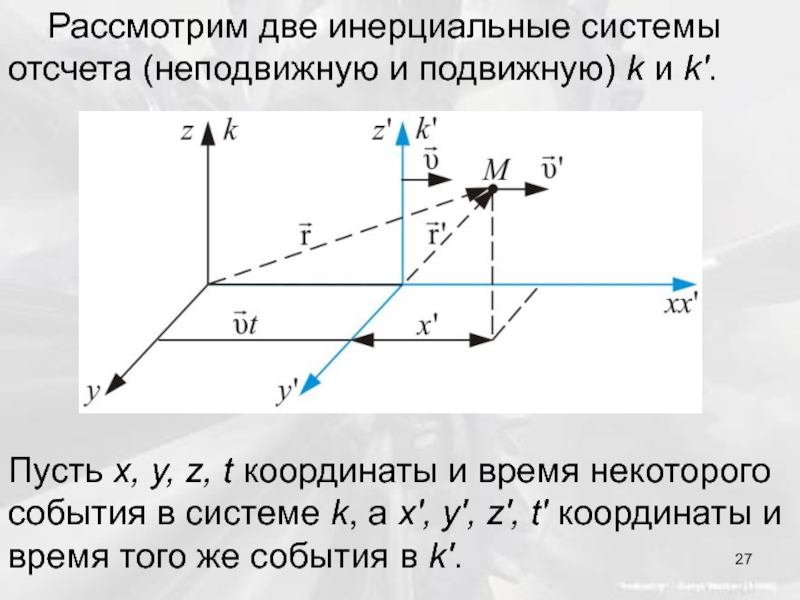
Слайд 27 Рассмотрим две инерциальные системы отсчета (неподвижную и подвижную) k и k'.
Пусть
Слайд 28Как связаны между собой эти координаты и время?
В рамках классической
эта связь устанавливается преобразованиями Галилея, в основе которых лежат представления об абсолютном пространстве и независимом времени:
Из этих преобразований следует, что взаимодействия, в том числе и электромагнит-ные, должны передаваться с бесконечно большой скоростью и, скорость движения сигнала в системе k, отличается от скорости в системе k':
Слайд 29
Лоренц установил связь между координатами и временем события
Слайд 30 - все инерциальные системы отсчета физически эквивалентны;
- скорость света в вакууме
Таким образом, при больших скоростях движения сравнимых со скоростью света, Лоренц получил
Слайд 32
Истинный физический смысл преобразований Лоренца был впервые установлен Эйнштейном в 1905
Слайд 33 Полученные уравнения связывают координаты и время в подвижной k' и неподвижной
При малых скоростях движения
или, при бесконечной скорости распрост-ранения взаимодействий теория дальнодействия), преобразования Лоренца переходят в преобразования Галилея (принцип соответствия).
(Разобрать самостоятельно)
Слайд 344. Следствия из преобразований Лоренца
1. Одновременность событий в СТО
По Ньютону, если
Эйнштейн задумался, как доказать одновременность?
Возьмем два источника света на Земле А и В:
Слайд 35Рисунок 8.4
Если свет встретится на середине АВ, то вспышки для человека
Слайд 36 Рассмотрим это более подробно.
Пусть в системе k (на Земле) в точках
Для определения координат в k' воспользуемся преобразованиями Лоренца
(4.1)
Слайд 38
События будут абсолютно одновременны в системах k и k', если они
в одном и том же месте
Если же в системе k
то из (8.4.1) и (8.4.2) видно, что и в k':
тогда из (8.4.3) и (8.4.4) видно, что события не одновременны, т.е.
Определим интервал времени между событиями в k':
Слайд 39
(4.5)
Разница во времени будет зависеть от
.
Интервал времени между событиями в k':
Слайд 402. Лоренцево сокращение длины
(длина тел в разных системах отсчета)
Пусть
Слайд 43 Формула называется Лоренцевым сокращением длины. Собственная длина
Длина движущегося тела короче, чем покоящегося.
Причем, сокращается только проекция на ось x, т.е. размер тела вдоль направления движения.
Слайд 443. Замедление времени
(длительность событий в разных системах отсчета)
Пусть вспышка лампы
Чему равна длительность вспышки с точки зрения человека находящего-ся на Земле, мимо которого пролетает ракета?
Так как тогда из преобразова-ний Лоренца:
Слайд 45
или
(4.7)
Из этого уравнения следует, что собственное время – минимально
Этот вывод имеет множество экспериментальных подтверждений.
Слайд 47 Так, нестабильные элементарные частицы – пионы, рождающиеся в верхних слоях атмосферы,
За это время они могут пройти путь
Но, в результате того, что они двигаются с очень большими скоростями, сравнимыми со скоростью света, их время жизни увеличивается и они до своего распада способны достигать поверхности Земли. Отсюда следует вывод, что у движущихся пионов секунды «длиннее» земных секунд.
Слайд 48 В 60 – 70 гг. замедление времени наблюдалось не только с
В 1971 г. Хафель и Китинг осуществили прямое измерение замедления времени, отправив два экземпляра атомных часов в кругосветное путешествие на реактивном самолете. Потом их показания сравнили с показаниями таких же часов, оставленных на Земле, в лаборатории ВМС США. Время запаздывания составило 273⋅ , что в пределах ошибок согласуется с теорией.
Слайд 49 Это следствие из преобразований Лоренца объясняет известный всем «парадокс близнецов» (самостоятельно).
Слайд 58
4. Сложение скоростей в релятивистской механике
Пусть тело внутри
и сам корабль движется с такой же скоростью
Чему равна скорость тела относительно Земли?
Используем для рассмотрения примера рисунок 8.2.
Слайд 59Классическая механика ответит на этот вопрос просто: в соответствии с преобразованиями
что, конечно же противоречит положению СТО о том, что скорость света является предельной скоростью переноса информации, вещества и взаимодействий:
Слайд 60 Оценим скорость тела, используя преобразования Лоренца.
Внутри корабля перемещение dx' за время
(4.8)
(4.9)
Слайд 61Так как
(4.10)
Эта формула выражает правило сложения скоростей в релятивистской кинематике.
Слайд 62 Подсчитаем скорость тела в нашем примере в соответствии полученной формулой:
Полученный результат
Слайд 63 При медленных движениях, когда
получаем нерелятивистские формулы, соответствующие преобразованиям Галилея.
(Проверить самостоятельно)
Если
(4.11)
Слайд 64 Полученные формулы сложения скоростей запрещают движение со скоростью больше скорости света.
Уравнения Лоренца преобразуют время и пространство так, что свет распространяется с одинаковой скоростью с точки зрения всех наблюдателей, независимо, двигаются они или покоятся.
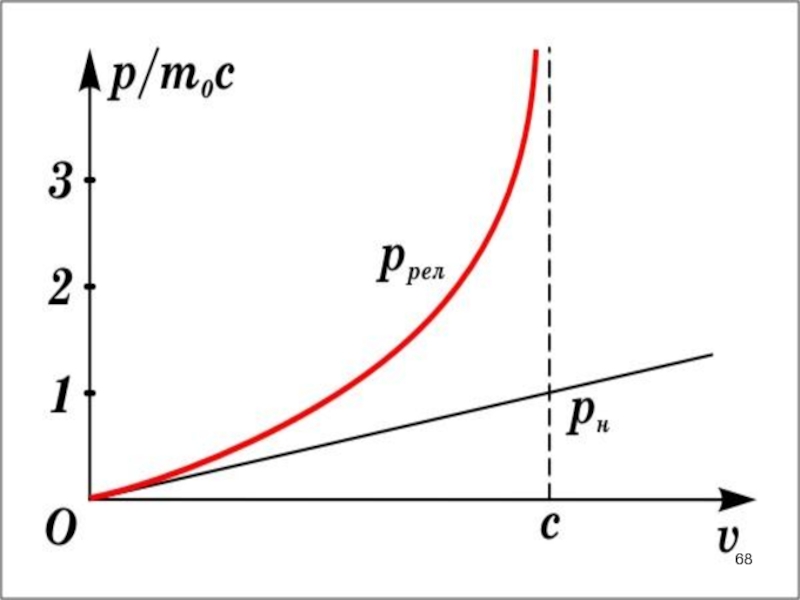
Слайд 66 Ньютоновское выражение для импульса
Вот это выражение надо сделать инвариантным. Это возможно если в него будут входить инвариантные величины.
Слайд 67
(5.2)
Это и есть релятивистское выражение для импульса.
Из (8.5.2) следует, что
знаменатель стремится к нулю, тогда
что невозможно в силу закона сохранения импульса).
Слайд 69
Релятивистское выражение для энергии
По определению
равна силе, действующей на частицу
Работа силы по перемещению частицы идет на увеличение энергии частицы:
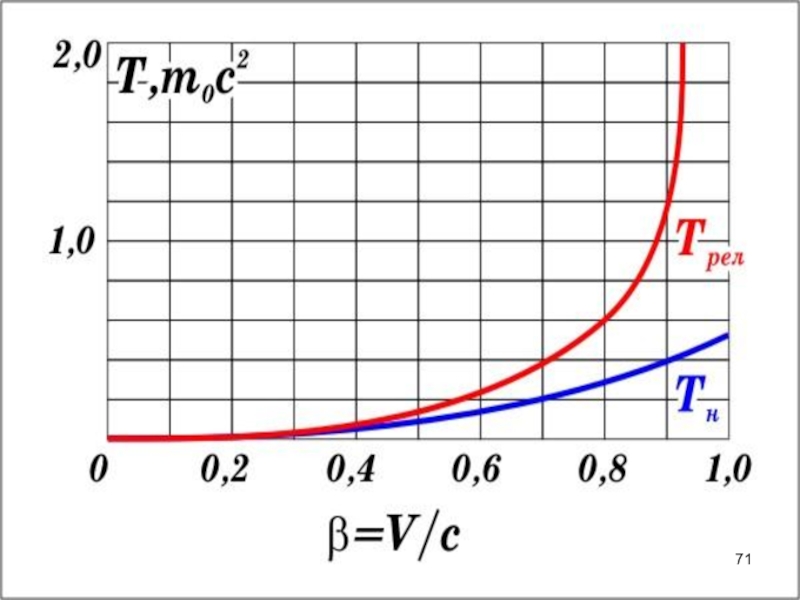
Слайд 70
После интегрирования этого выражения получим релятивистское выражение для энергии частицы:
где Е – полная энергия.
При в системе координат, где частица покоится, выражение (8.5.3) преобразуется:
(5.4)
– энергия покоя частицы.
Слайд 72 Именно утверждение о том, что в покоящейся массе (материи) огромные запасы
Полная энергия в теории относительности складывается из энергии покоя и кинетической энергии (К). Тогда
Слайд 74 Получим еще одно очень важное соотношение, связывающее полную энергию с импульсом
Из уравнения
получим:
Таким образом, получили инвариантное выражение, связывающее энергию и импульс.
Слайд 756. Взаимосвязь массы и энергии покоя
Масса и энергия покоя связаны соотношением:
из которого вытекает, что всякое изменение массы Δm сопровождается изменением энергии покоя ΔE0.
Это утверждение носит название взаимосвязь массы и энергии покоя и стало символом современной физики.
Слайд 76 Взаимосвязь между массой и энергией оценивалась А. Эйнштейном как самый значительный
Слайд 77Эйнштейна имеем
Таким
Из этого примера видно, что если высвобождается лишь одна тысячная доля собственной энергии, то и это количество в миллионы раз больше того, что могут дать обычные источники энергии.
Определим энергию, содержащуюся в 1 г. любого вещества, и сравним ее с химической энергией, получаемой при сгорании 1 г. угля равной . Согласно уравнению
Слайд 78 Пример: пусть две одинаковые по массе частицы m движутся с одинаковыми
До соударения полная энергия каждой
частицы Е равна:
Полная энергия образовавшейся частицы
(эта новая частица имеет скорость ). Из закона сохранения энергии:
При взаимодействии частиц суммарная масса взаимодействующих частиц не сохраняется.
Слайд 79
откуда М равно:
(6.2)
Таким образом, сумма масс исходных частиц 2m, меньше
В этом примере, кинетическая энергия частиц превратилась в эквивалентное количество энергии покоя, а это привело к возрастанию массы
Слайд 80
(это при отсутствии выделения энергии при соударении частиц).
Выражение «масса покоя» можно
Пусть система (ядро) состоит из N частиц с массами m1, m2…mi. Ядро не будет распадаться на отдельные частицы, если они связаны друг с другом. Эту связь можно охарактеризовать энергией связи Eсв.
Слайд 81 Энергия связи – энергия которую нужно затратить, чтобы разорвать связь между
(6.3)
где ΔМ – дефект массы.
Видно, что Есв будет положительна, если
Слайд 82 Это и наблюдается на опыте.
При
Например, ядро U238 имеет энергию связи
Eсв = 2,9⋅10–10 Дж ≈1,8⋅109 эВ = 1,8 ГэВ.
Слайд 83Ядерные реакции
Ядерной реакцией называется процесс взаимодействия атомного ядра с элемен-тарной частицей
Это реакция взаимодействия протона с ядром лития. Реакция протекает с выделением энергии.
Слайд 84
В ядерной энергетике большой практический интерес имеют реакции с участием нейтронов,
Реакция протекает при захвате ядрами
медленных нейтронов.
Ядра иттрия и йода – это осколки деления. Ими могут быть и другие ядра.
Слайд 85 Характерно, что в каждом акте деления возникает 2 – 3 нейтрона,
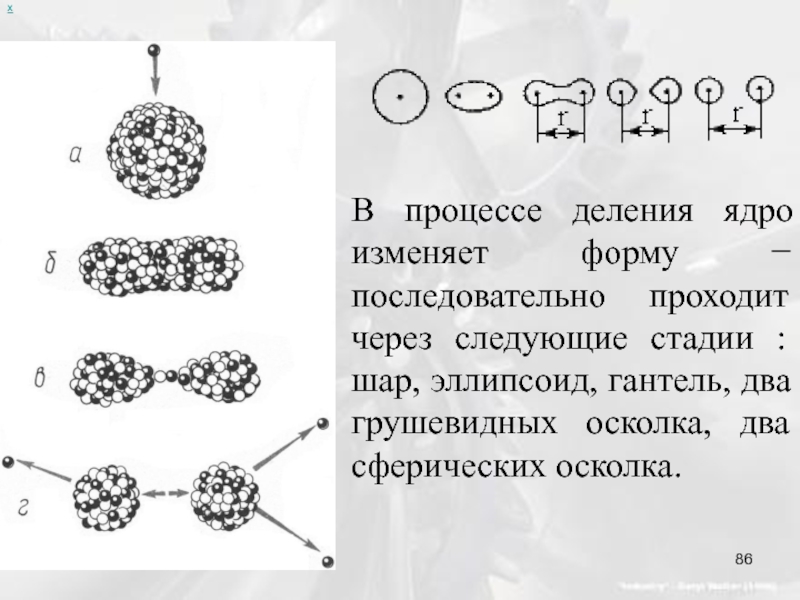
Слайд 86х
В процессе деления ядро изменяет форму − последовательно проходит через следующие
Слайд 88 Его основные элементы: ядерное топливо, замедлитель нейтронов, теплоноситель для отвода
Устройство, в котором поддержи-вается управляемая реакция деления атомных ядер, называется ядерным реактором.
Слайд 89х
Первая атомная электростанция мощностью 5 МВт была построена пущена в СССР
Слайд 91Конструктивная схема реактора на быстрых нейтронах типа БН-600 Корпусной –
Слайд 94
Термоядерные реакции
Термоядерные реакции – это реакции синтеза легких ядер, протекающие при
(10–15 м).
Слайд 95 Энергия, выделяющаяся в процессе термоядерных реакций в расчете на один нуклон,
Слайд 96
наиболее перспективна в плане получения практически неисчерпаемого источника энергии. Однако, осуществление
Термоядерная реакция синтеза дейтерия с тритием:
Слайд 97 В настоящее время, в рамках осуществления мировой термоядерной программы, интенсивно разрабатываются
Слайд 98На рисунке 4.12 изображена схема токамака: 1 – первичная обмотка трансформатора;
Слайд 100
Есть надежда, что термоядерный реактор практического применения будет создан уже в
Слайд 101
При ядерных реакциях выделяется в виде энергии не более 0,1
Полностью энергия покоя выделяется только при аннигиляции, в виде электромагнитного излучения, как например, при аннигиляции электрона и позитрона