- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Сопротивление материалов. (Лекция 1) презентация
Содержание
- 1. Сопротивление материалов. (Лекция 1)
- 2. Литература: Стёпин П.А. Сопротивление материалов: Учебное
- 3. ВВЕДЕНИЕ Сопротивление материалов - это
- 4. Прочность - называется способность деталей или элементов
- 5. Сопротивление материалов Теоретическая часть Теоретическая механика Экспериментальная часть Математика Физика Материало-ведение
- 6. В сопротивлении материалов расчёт любого реального материального
- 7. Реальный объект, освобожденный от несущественных особенностей, называется
- 8. Модели формы Первая группа элементов –
- 9. Оболочкой называется геометри-ческое тело, длина и ширина
- 10. Пластиной называется оболочка с плоской поверхностью
- 11. Четвертая группа элементов – это элементы, у
- 12. Стержнем называется геометричес-кое тело, два размера которого
- 13. 1. Допущения о свойствах материалов: (модели материалов)
- 14. Сплошность – понятие, предполагающее, что материал полностью
- 15. 2. Допущения о деформациях: Упругие (обратимые) деформации
- 16. В сопротивлении материалов приняты следующие гипотезы:
- 17. Гипотеза плоских сечений (гипотеза
- 18. Классификация сил и нагрузок. Внешние силы –это
- 19. Объемные (массовые) силы приложены к каждой частице
- 20. Силы, системы сил. Сила-это количественная
- 21. Вектор изображается отрезком, на конце
- 22. Системой сил называется совокупность нескольких
- 23. 0 (1) (3) (2) (4)
- 24. Эквивалентные системы сил это такие системы, которые
- 25. Равнодействующая двух сходящихся сил,
- 26. У + + F1 F2 F1
- 27. Пара сил и моменты сил.
- 28. а F F 90о
- 29. Классификация внешних сил Внешние силы
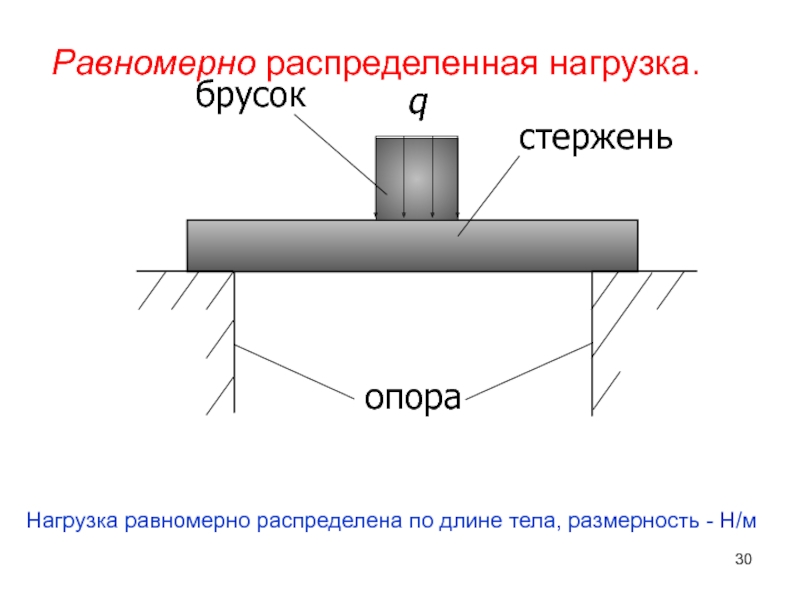
- 30. q Равномерно распределенная нагрузка. Нагрузка равномерно распределена по длине тела, размерность - Н/м
- 31. Примером действия равномерно распределённой нагрузки по площади
- 32. Ω- площадь фигуры, ограничивающей действие распределённой нагрузки. Произвольно распределенная нагрузка.
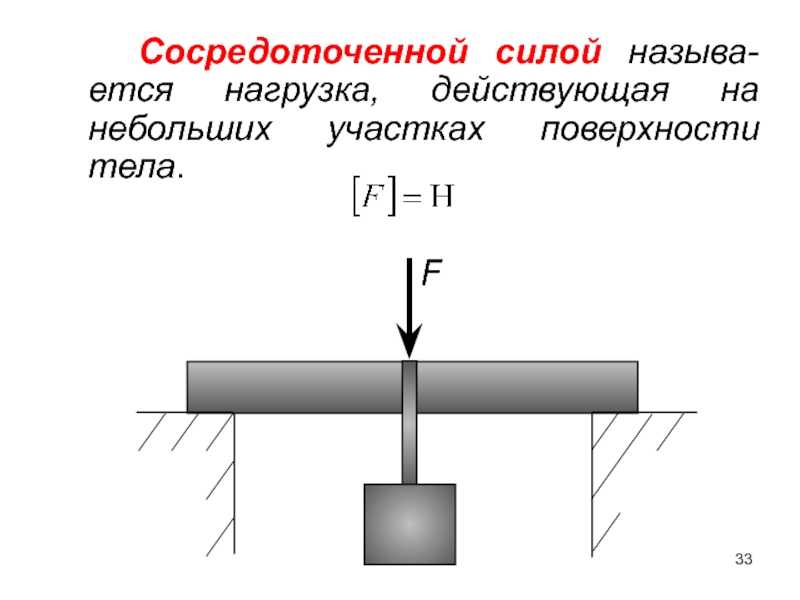
- 33. Сосредоточенной силой называ-ется нагрузка, действующая на небольших участках поверхности тела. F
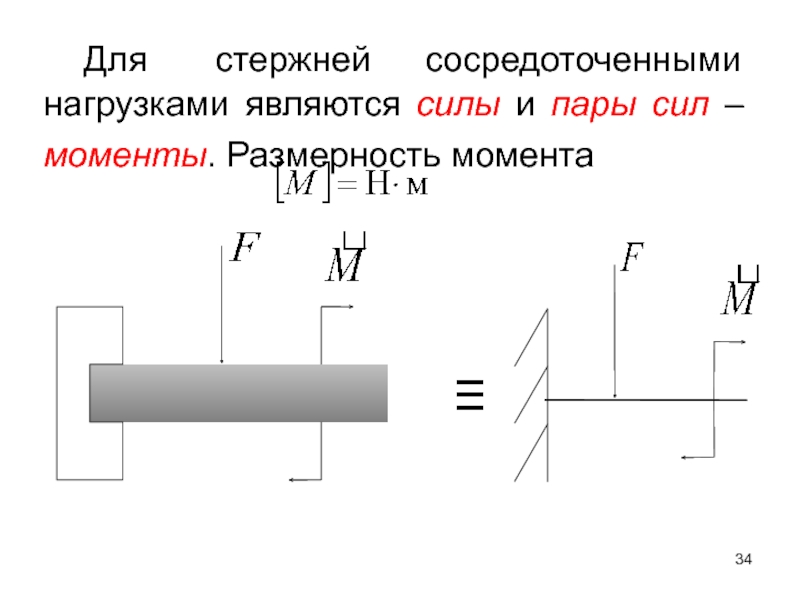
- 34. Для стержней сосредоточенными нагрузками являются силы и пары сил – моменты. Размерность момента
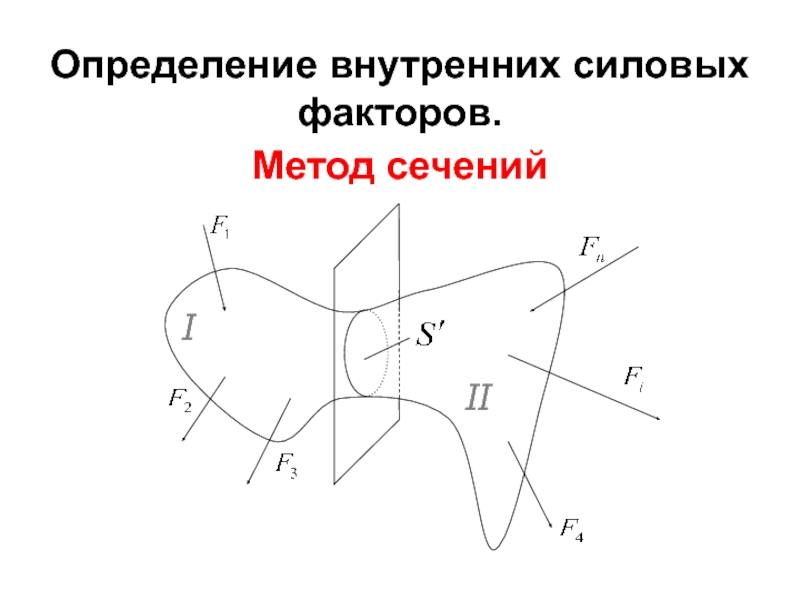
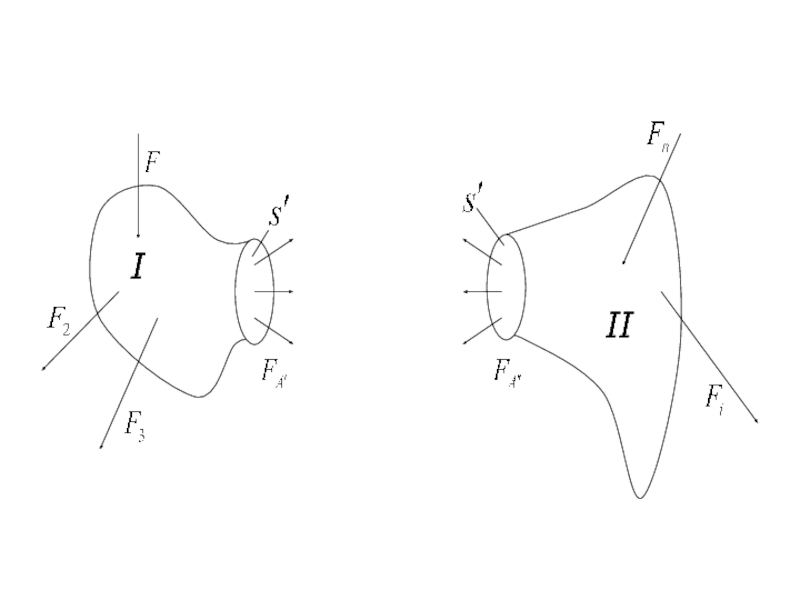
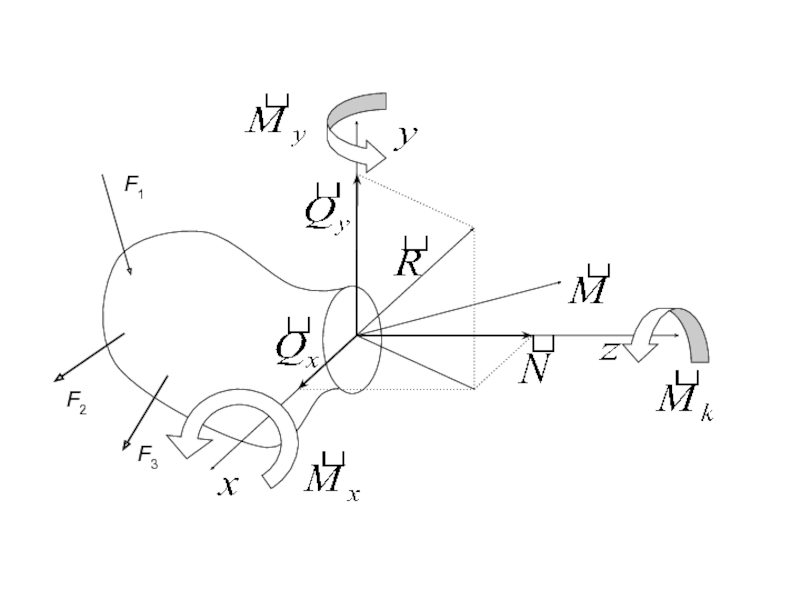
- 35. Определение внутренних силовых факторов. Метод сечений
- 38. Назовем силу, параллельную оси z, нормальной или
- 39. Перечисленные силы и моменты называются внутренними силовыми
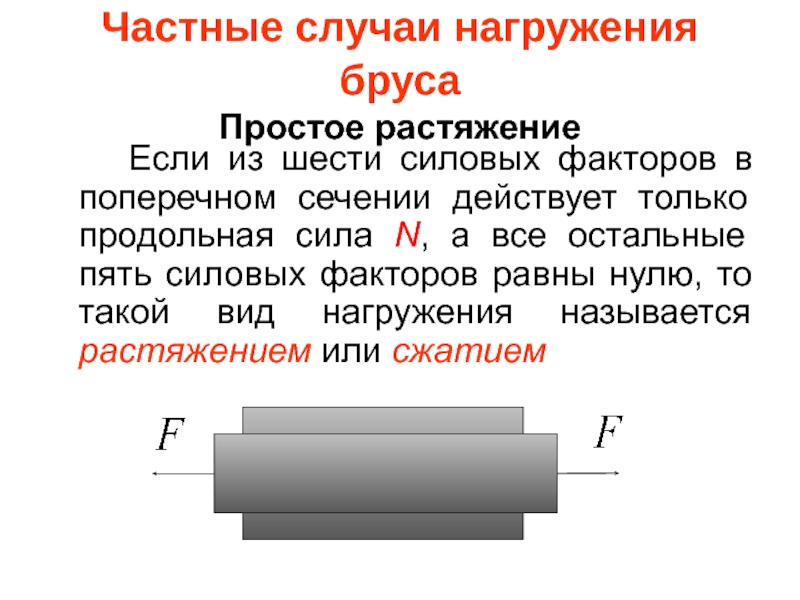
- 40. Частные случаи нагружения бруса Простое растяжение
- 41. Если внешняя сила F действует
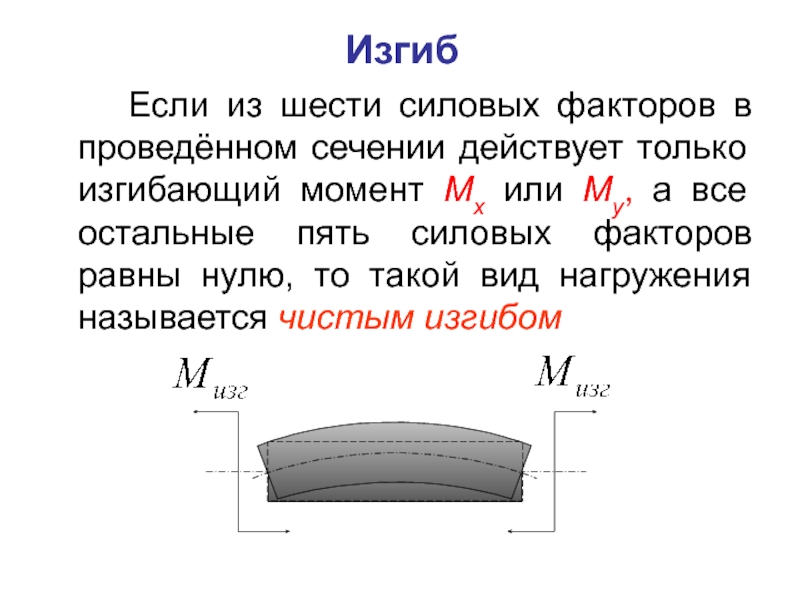
- 42. Если из шести силовых факторов в проведённом
- 43. Кручение Кручением называется такой вид нагружения
- 44. Правило знаков Положительным
- 45. Если из шести силовых факторов в проведённом
- 46. Если из шести силовых факторов в проведённом
- 47. Правила знаков Поперечная сила
- 48. Изгибающий момент считается положительным, если
- 49. Дифференциальные зависимости при изгибе Рассмотрим консольную
- 50. Полная производная от изгибающего
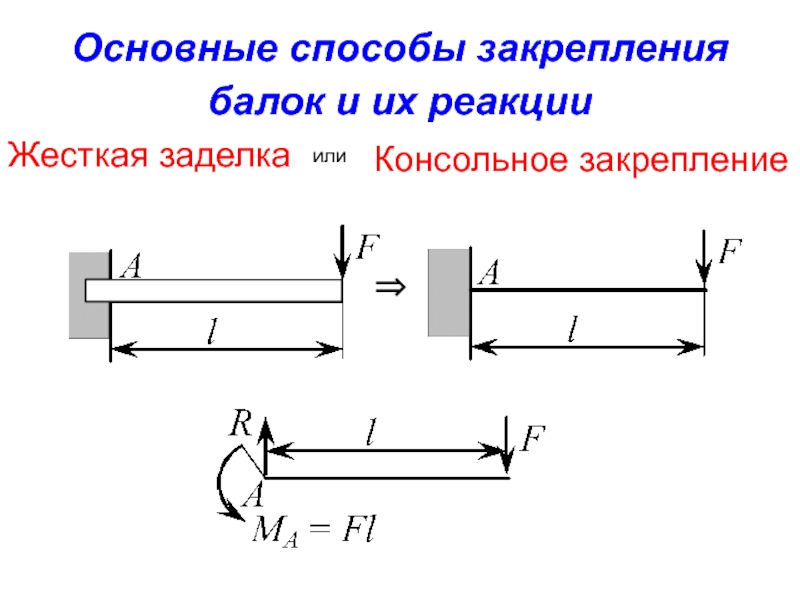
- 51. Основные способы закрепления балок и их реакции
- 52. Шарнирно – неподвижная опора. ⇒ Шарнирно – подвижная опора. ⇒
- 53. Определение опорных реакций. Для плоской системы можно
Слайд 1Прикладная механика
Лектор:
доцент кафедры
«Техническая механика»
Коротаева
Татьяна Петровна
Лекция № 1
Слайд 2Литература:
Стёпин П.А. Сопротивление материалов: Учебное издание. – М: Изд-во «Высшая школа»,
Феодосьев В.И. Сопротивление материалов: Учебное издание. – М: Изд-во МГТУ им. Н.Э. Баумана, 2000. – 591 с
Обищенко Л.Н., Певнев В.Г., Лазько Н.В. «Механика», раздел «Сопротивление материалов»,методическое пособие. – РГУ, 2008г.
Слайд 3ВВЕДЕНИЕ
Сопротивление материалов - это раздел механики, в котором рассматриваются твердые
Основной задачей СМ является разработка инженерных методов расчета элементов конструкций на прочность, жесткость и устойчивость.
Слайд 4 Прочность - называется способность деталей или элементов конструкции сопротивляться воздействию внешних
Жесткость - способность деталей и элементов конструкции сопротивляться образованию деформации, т.е. изменению первоначальных размеров и формы.
Устойчивость - способность конструкции сохранять первоначальную форму равновесия под нагрузкой.
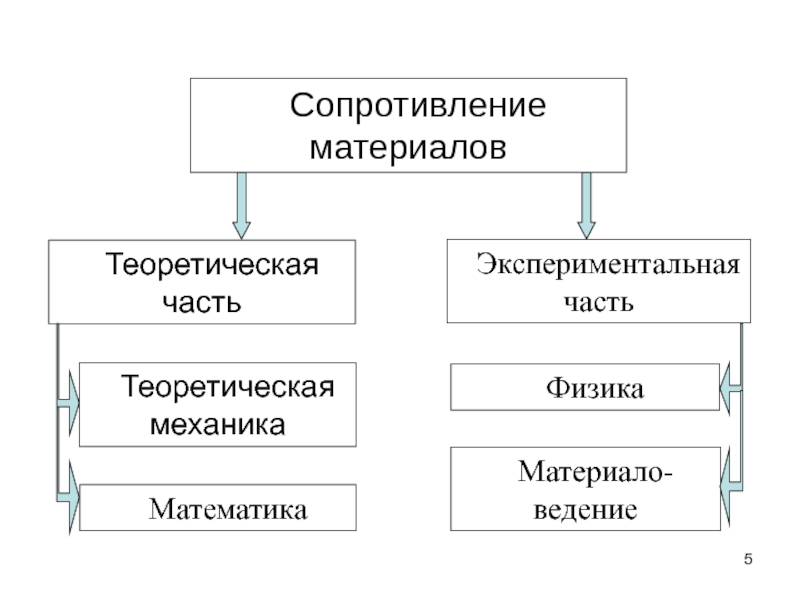
Слайд 5Сопротивление материалов
Теоретическая часть
Теоретическая механика
Экспериментальная часть
Математика
Физика
Материало-ведение
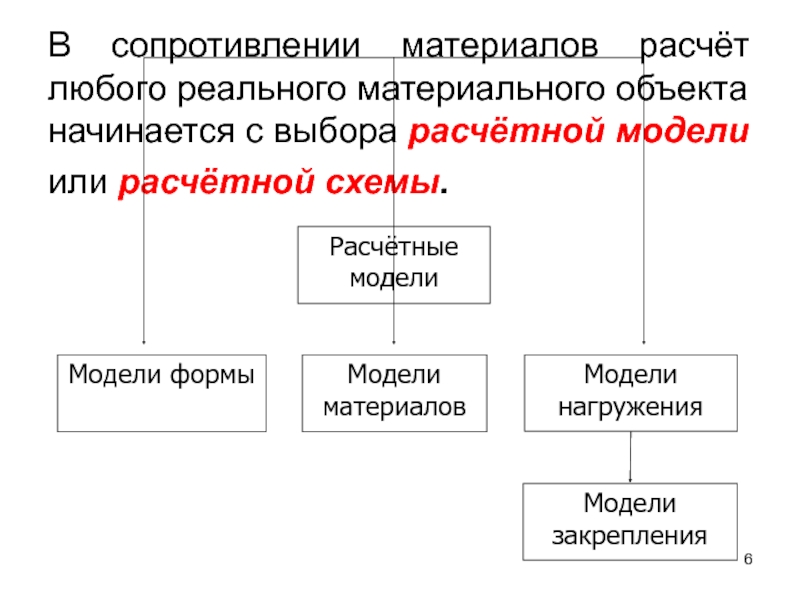
Слайд 6В сопротивлении материалов расчёт любого реального материального объекта начинается с выбора
Расчётные модели
Модели формы
Модели материалов
Модели нагружения
Модели закрепления
Слайд 7Реальный объект, освобожденный от несущественных особенностей, называется расчетной схемой.
При расчётах производится схематизация формы реального объекта по геометрическим признакам.
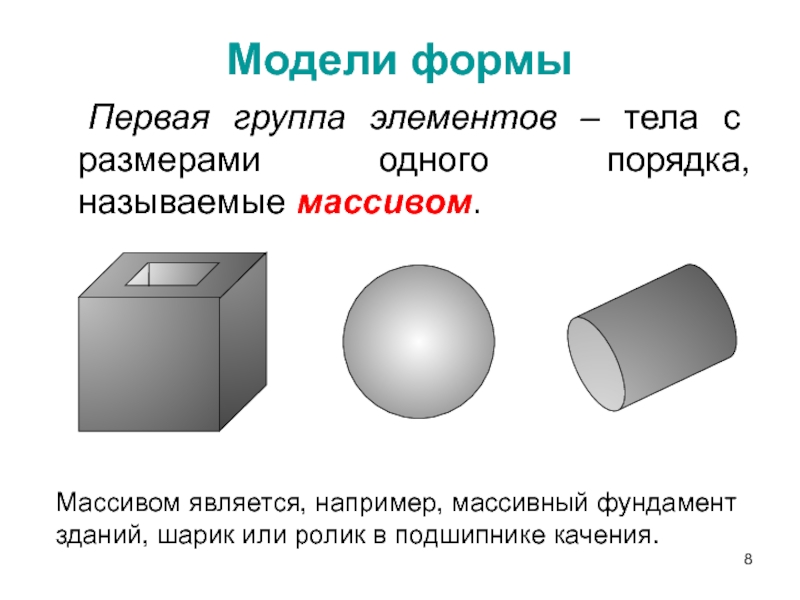
Слайд 8Модели формы
Первая группа элементов – тела с размерами одного порядка,
Массивом является, например, массивный фундамент зданий, шарик или ролик в подшипнике качения.
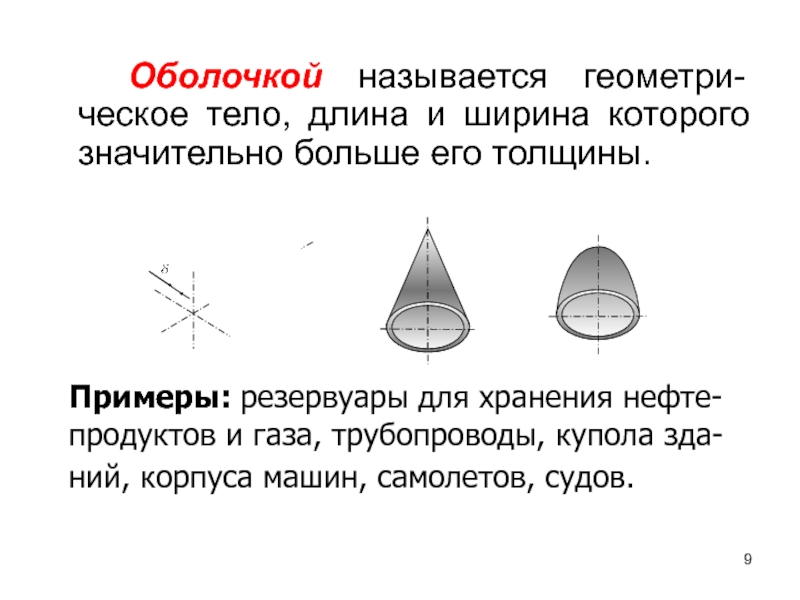
Слайд 9 Оболочкой называется геометри-ческое тело, длина и ширина которого значительно больше его
Примеры: резервуары для хранения нефте-продуктов и газа, трубопроводы, купола зда-ний, корпуса машин, самолетов, судов.
Слайд 10Пластиной называется оболочка с плоской поверхностью
Примеры: плоские днища и крышки
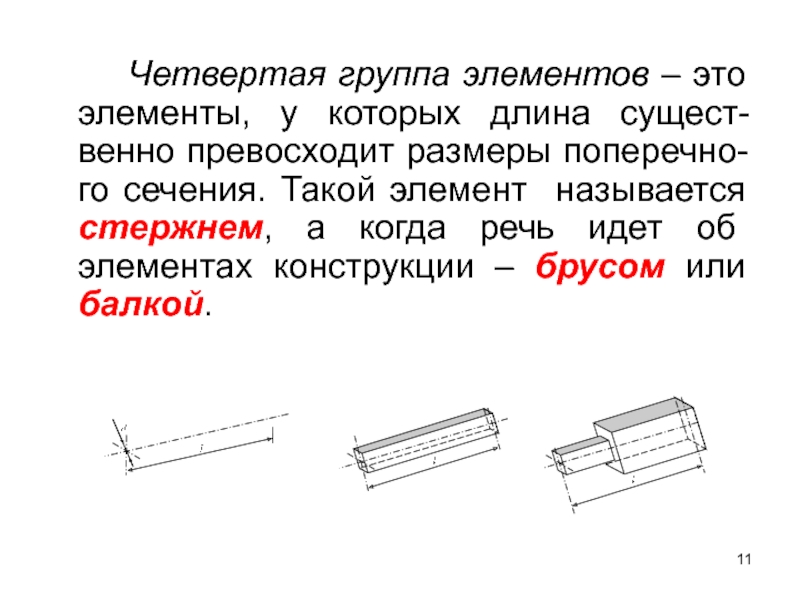
Слайд 11 Четвертая группа элементов – это элементы, у которых длина сущест-венно превосходит
Слайд 12 Стержнем называется геометричес-кое тело, два размера которого намного меньше его третьего
Стержни бывают прямолинейные, криволинейные, с постоянным сечени-ем, с переменным сечением; с комбини-рованным сечением.
Примеры стержней: оси, валы, крюки, пружины, звенья цепей и т.д.
Слайд 131. Допущения о свойствах материалов: (модели материалов)
материал считается:
сплошным;
однородным;
изотропным;
идеально-упругим.
Допущения и гипотезы
в
Слайд 14Сплошность – понятие, предполагающее, что материал полностью заполняет занимаемый объем и
Однородность –свойства материала во всех точках тела одинаковы.
Изотропность - свойства материала во всех направлениях одинаковы.
Пример: сталь изотропна, дерево анизотропно.
Идеальная упругость – свойство полностью восстанавливать форму и размеры после устранения причин, вызвавших эти изменения.
Слайд 152. Допущения о деформациях:
Упругие (обратимые) деформации – исчезают после устранения причин,
Пластические (необратимые) деформации – остаются после устранения причин, их вызвавших (например, после снятия нагрузки).
Слайд 16 В сопротивлении материалов приняты следующие гипотезы:
Гипотеза об отсутствии первоначальных внутренних усилий.(До
Гипотеза независимости действия сил.(Результат действия системы сил равен сумме результатов действия этих же сил, приложенных в любой последовательности).
Слайд 17Гипотеза плоских сечений (гипотеза Бернулли) – сечения, перпендикулярные
Принцип Сен-Венана – напряженное состояние тела на достаточном удалении от области действия локальных нагрузок очень мало зависит от способа их приложения.
Слайд 18Классификация сил и нагрузок.
Внешние силы –это результат действия на тело других
Внутренние силы – это усилия, возникающие между всеми соседними частицами внутри тела, под воздействием нагрузки (внешних сил).
Слайд 19 Объемные (массовые) силы приложены к каждой частице объема (массы) материала.
Поверхностные
Внешние силы разделяются на поверхностные и объёмные.
Слайд 20Силы, системы сил.
Сила-это количественная мера механического взаимодействия твердых тел.
Числовым значением (модулем).
Точкой приложения.
Направлением.
Сила-это векторная величина.
Слайд 21
Вектор изображается отрезком, на конце которого ставится стрелка.
Вектор обозначается буквой с
Величина вектора обозначается той же буквой только без черточки.
Модуль, или величина силы, является количественной характеристикой меры взаимодействия тел и измеряется в ньютонах
(Н). ( Примером силы может служить сила тяжести)
Линией действия силы называют прямую, проведённую по направлению силы неограниченно в обе стороны.
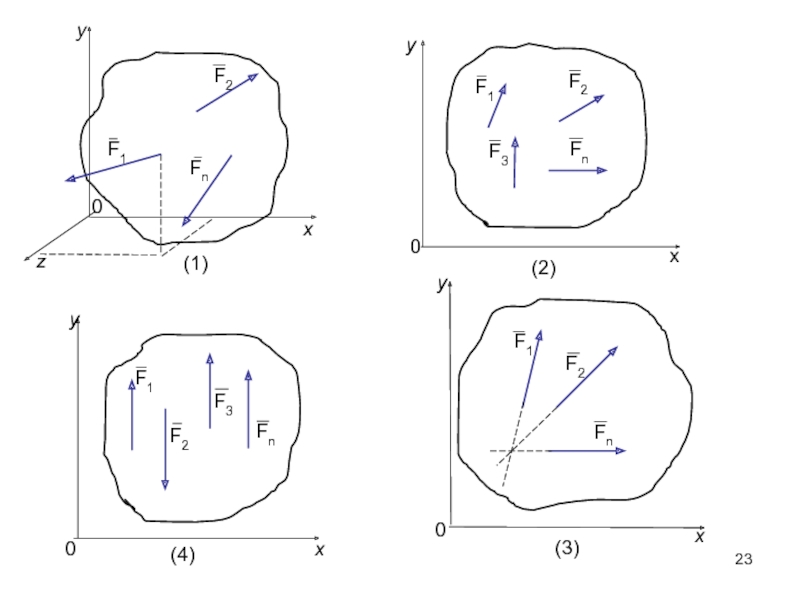
Слайд 22 Системой сил называется совокупность нескольких сил, приложенных к телу.
(2).Плоская система – линии действия сил лежат в одной плоскости.
(3).Система сходящихся сил – линии действия сил пересекаются в одной точке.
(4).Система параллельных сил – линии действия сил параллельны.
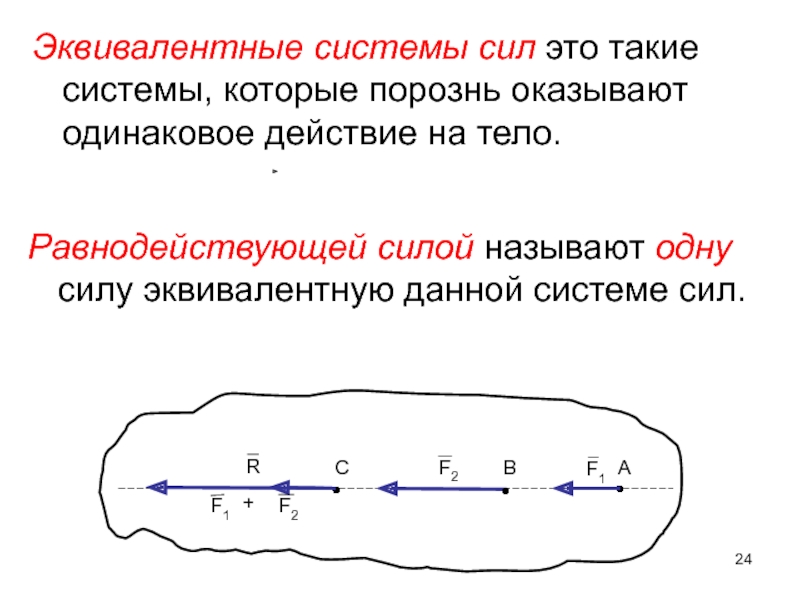
Слайд 24Эквивалентные системы сил это такие системы, которые порознь оказывают одинаковое действие
Равнодействующей силой называют одну силу эквивалентную данной системе сил.
А
B
C
R
F1
+
F2
Слайд 25 Равнодействующая двух сходящихся сил, приложенных к одной точке,
Всякую силу, действующую на твёрдое тело, можно перенести вдоль линии её действия в любую точку тела, не нарушив при этом его равновесия.
Силы, приложенные к телу, Можно складывать, определяя равнодействующую, и раскладывать на составляющие.
Слайд 26
У
+
+
F1
F2
F1
F2
Уравновешивающая сила (У) – это сила численно равная
равнодействующей, но направлена по
Слайд 27Пара сил и моменты сил.
Система двух равных и
Сумма сил пары равна нулю, т.е. пара сил не имеет равнодействующей.
Пара сил стремится вращать тело по часовой стрелке (-), либо против (+).
Количественно действие пары определяется моментом пары, равным произведению силы на кратчайшее расстояние между линиями действия этих сил. Размерность момента – Н.м
Следствие: Момент пары равен произведению силы на плечо.
Слайд 28
а
F
F
90о
-
+
а
F
F
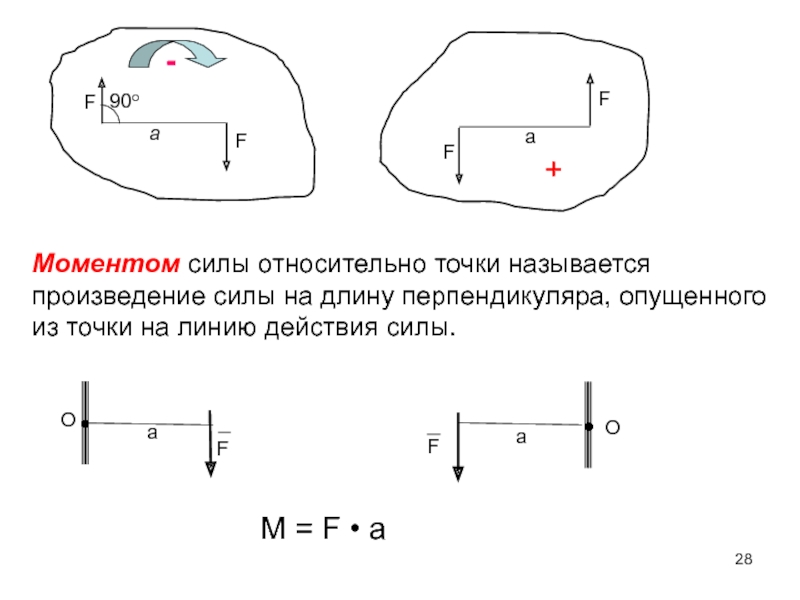
Моментом силы относительно точки называется произведение силы на длину перпендикуляра,
М = F • а
Слайд 29Классификация внешних сил
Внешние силы (нагрузка) подразделяются на распределенные и сосредоточенные.
Распределенной
Распределенная нагрузка подразделяется на равномерно и произвольно распределенную по длине либо по некоторой площади поверхности тела
Размерность интенсивности нагрузки, распределенной по длине поверхности тела
Слайд 30
q
Равномерно распределенная нагрузка.
Нагрузка равномерно распределена по длине тела, размерность - Н/м
Слайд 31 Примером действия равномерно распределённой нагрузки по площади поверхности тела является
Нагрузка распределена по некоторой площади поверхности тела, размерность – Н/м2
Слайд 32 Ω- площадь фигуры, ограничивающей действие распределённой нагрузки.
Произвольно распределенная нагрузка.
Слайд 33 Сосредоточенной силой называ-ется нагрузка, действующая на небольших участках поверхности тела.
F
Слайд 34 Для стержней сосредоточенными нагрузками являются силы и пары сил – моменты.
Слайд 38 Назовем силу, параллельную оси z, нормальной или продольной силой N.
Параллельные
Момент силы, действующий относительно
оси z, называется
крутящим моментом Mк или Т.
Моменты сил, действующие относительно осей x и y –
изгибающими моментами Mx и My.
Слайд 39 Перечисленные силы и моменты называются внутренними силовыми факторами. Для определения внутренних
Слайд 40Частные случаи нагружения бруса
Простое растяжение
Если из шести силовых факторов в
Слайд 41 Если внешняя сила F действует от сечения, то она вызывает растяжение
Если внешняя сила F действует к сечению, то она вызывает сжатие (уменьшение длины бруса) и сила N в сечении считается отрицательной (N < 0 – сжатие).
Брусья, в основном работающие на растяжение-сжатие, называются стержнями.
Слайд 42 Если из шести силовых факторов в проведённом сечении действует только поперечная
Слайд 43Кручение
Кручением называется такой вид нагружения бруса, при котором в его
Примером детали, работающей на кручение, является вал.
При действии разнонаправленных крутящих моментов одинаковой величины в противоположных торцах вала, он будет закручиваться, сечения вала будут поворачиваться относительно друг друга, а длина вала будет оставаться неизменной.
Слайд 44Правило знаков
Положительным считается крутящий момент, направленный против
Отрицательным считается крутящий момент, направленный по часовой стрелке, если смотреть на сечение со стороны внешней нормали.
Правило знаков для крутящего момента условно (в отличие от правил знаков для растяжения-сжатия), т.к. материал бруса одинаково ведет себя при кручении в разных направлениях.
Слайд 45 Если из шести силовых факторов в проведённом сечении действует только изгибающий
Изгиб
Слайд 46 Если из шести силовых факторов в проведённом сечении действует только изгибающий
В остальных случаях нагружение называется сложным нагружением или сложным сопротивлением.
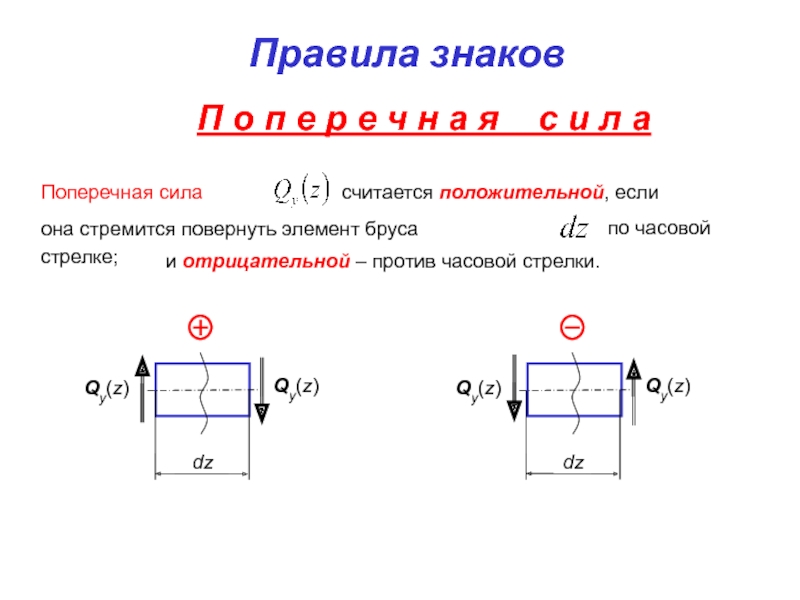
Слайд 47Правила знаков
Поперечная сила
считается положительной, если
она стремится повернуть элемент
по часовой
стрелке;
и отрицательной – против часовой стрелки.
П о п е р е ч н а я с и л а
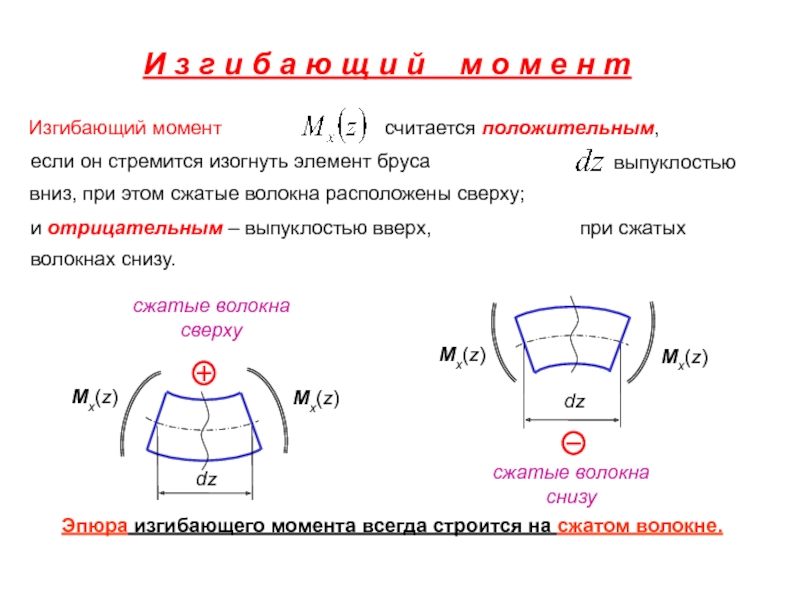
Слайд 48Изгибающий момент
считается положительным,
если он стремится изогнуть элемент бруса
выпуклостью
вниз,
и отрицательным – выпуклостью вверх,
при сжатых
волокнах снизу.
сжатые волокна
сверху
И з г и б а ю щ и й м о м е н т
сжатые волокна
снизу
Эпюра изгибающего момента всегда строится на сжатом волокне.
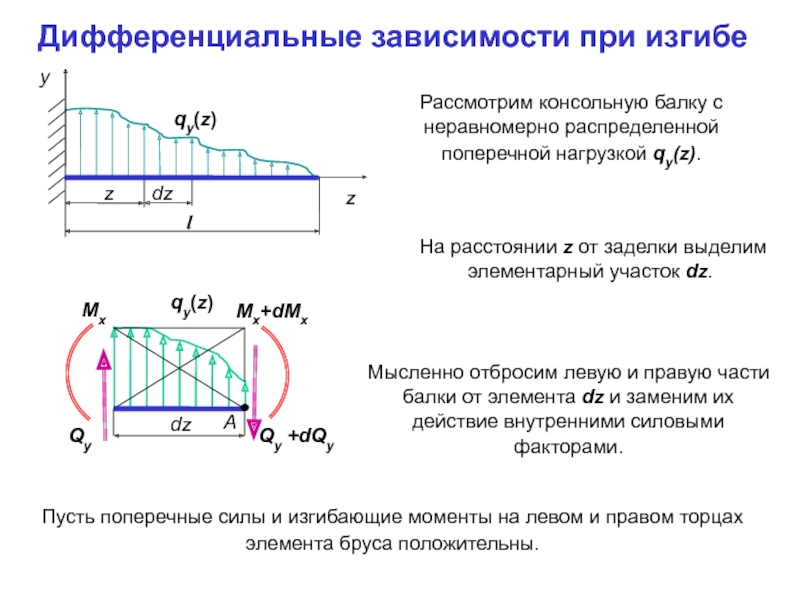
Слайд 49Дифференциальные зависимости при изгибе
Рассмотрим консольную балку с неравномерно распределенной поперечной
На расстоянии z от заделки выделим элементарный участок dz.
Мысленно отбросим левую и правую части балки от элемента dz и заменим их действие внутренними силовыми факторами.
Пусть поперечные силы и изгибающие моменты на левом и правом торцах элемента бруса положительны.
Слайд 50
Полная производная от изгибающего момента по z равна поперечной силе;
Составим
Слайд 53Определение опорных реакций.
Для плоской системы можно составить три уравнения
равновесия:
Правила знаков:
Силы,
вниз – отрицательными (-)
Моменты сил, направленные по часовой стрелке, считаются
отрицательными (-), против – положительными (+)