- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Сложение потенциальных потоков презентация
Содержание
- 1. Сложение потенциальных потоков
- 2. Лекция 6 Плоское потенциальное движение
- 3. Сложение потенциальных потоков Если поток является результатом
- 4. Сложение потенциальных потоков Сложение параллельного течения и
- 5. Сложение потенциальных потоков Легко показать, что на
- 6. Сложение потенциальных потоков Направление результирующих скоростей в точках, лежащих нa оси у определится формулой
- 8. Сложение потенциальных потоков Видно, что угол
- 9. Сложение потенциальных потоков Уравнение Бернулли полностью остается
- 10. Отсюда эта ширина b определяется уравнением:
- 11. Сложение потенциальных потоков α1 s1 α2 α2-α1
- 12. Сложение потенциальных потоков
- 13. Сложение потенциальных потоков Cкорость с направлена по
- 14. Сложение потенциальных потоков Диполь Если предположить,
- 15. Сложение потенциальных потоков Однако, можно рассматривать расстояние
- 16. Сложение потенциальных потоков Эта пара «источник-сток» называется
- 17. Сложение потенциальных потоков Влияние диполя убывает
- 18. Сложение потенциальных потоков Сложение параллельного течения с
- 19. Влево от точки А скорость с пары
- 20. Сложение потенциальных потоков Вторая критическая точка имеет
- 21. Сложение потенциальных потоков Сложение источника и вихря
- 22. Сложение потенциальных потоков Угол α величина постоянная
- 23. Сложение потенциальных потоков В пространстве между двумя
Слайд 3Сложение потенциальных потоков
Если поток является результатом сложения двух потенциальных течений, то
Потенциал скоростeй сложного двuженuя получается методом наложения по принципу независимости действия сил, т. е. потенциал скорости равен алгебраической сумме потенциалов скоростей слагаемых потоков.
Слайд 4Сложение потенциальных потоков
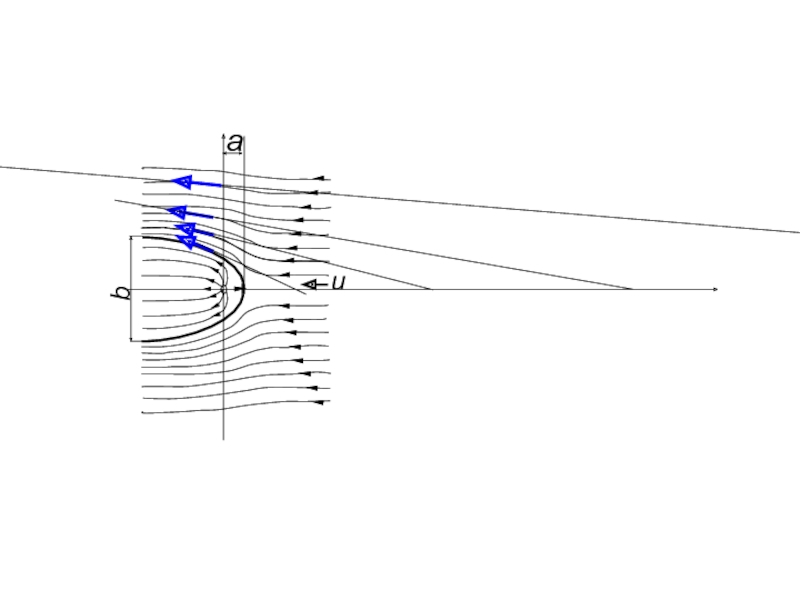
Сложение параллельного течения и источника
Исследуем тип течения, образующегося при
Точку, где помеща-ется источник, примем за начало координат.
х
у
Распределение скоростей вокруг источника задает-ся формулой
Слайд 5Сложение потенциальных потоков
Легко показать, что на оси х течения должна существовать
Такие точки течения, в которых скорость жидкости равна нулю, встречаются и при других типах течения. Эти точки обычно называются критическими, напорными.
Расстояние а этой точки от источника определяется paвенством
Слайд 6Сложение потенциальных потоков
Направление результирующих скоростей в точках, лежащих нa оси у
Слайд 8Сложение потенциальных потоков
Видно, что угол наклона этих скоростей к оси х,
При отсутствии трения ничто не препятствует замене этой кривой твердой стенкой, т. е. приходим к течению, имеющему место при обтекании спереди закругленного бесконеч-но длинного тела
Слайд 9Сложение потенциальных потоков
Уравнение Бернулли полностью остается в силе и после наложения
конечности все линии тока становятся парал-
лельными, а потому и давления должны быть одинаковыми в плоскостях, перпендикулярных направлению течения.
Но это возможно лишь при равенстве скоростей, т. е. когда лента шириной b, в которую переходит течение от источника в бесконечности (что совпадает с шириной обтекаемого тела в бесконечности), также приобретает скорость u.
Слайд 10Отсюда эта ширина b определяется уравнением:
b ·и = Q;
b =
К этой величине асимптотически приближается шири-
на бесконечно длинного обтекаемого тела.
Слайд 11Сложение потенциальных потоков
α1
s1
α2
α2-α1
α2-α1
s2
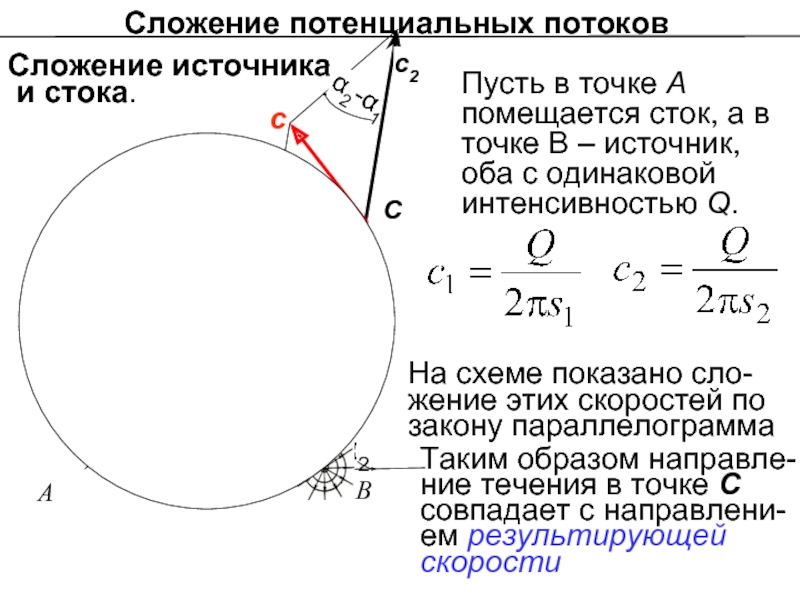
Пусть в точке А помещается сток, а в точке
На схеме показано сло-жение этих скоростей по закону параллелограмма
Сложение источника
и стока.
С
Таким образом направле-ние течения в точке С совпадает с направлени-ем результирующей скорости
Слайд 13Сложение потенциальных потоков
Cкорость с направлена по касатeльной к окружности, проходящей через
Линия, огибающая все векторы скорости является не чем иным, как траекторией частицы.
Линиu mокa результирующего течения (источник+сток) представляют собой nучок окружностей, nроходящuх через точки А и В.
Слайд 14Сложение потенциальных потоков
Диполь
Если предположить, что источник и сток помещаются в
Слайд 15Сложение потенциальных потоков
Однако, можно рассматривать расстояние между источником и стоком l
Результирующая скорость в точке С
при l равном нулю, тоже обратится в ноль. Но есть возможность, уменьшая l, увеличивать Q для соблюдения равенства
Слайд 16Сложение потенциальных потоков
Эта пара «источник-сток» называется диполем. Произведение Q·l=М – момент
Момент диполя - величина постоянная, линии тока - семейство окружностей, так как s1= s2=r. Тогда скорость в точке на расстоянии r от центра диполя определяется формулой
Эта формула верна, и в случае конечных расстояний между источником и стоком, но лишь для точек, находящихся на большом расстоянии от них.
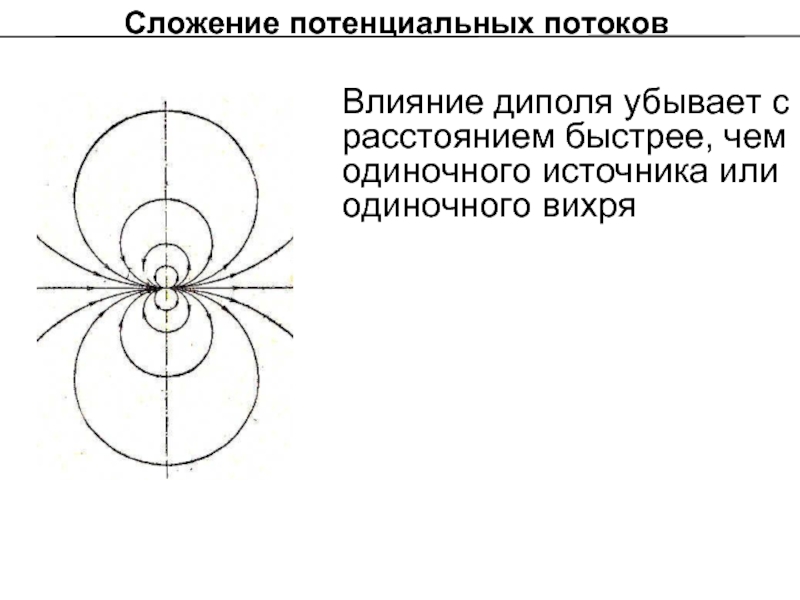
Слайд 17Сложение потенциальных потоков
Влияние диполя убывает с расстоянием быстрее, чем одиночного источника
Слайд 18Сложение потенциальных потоков
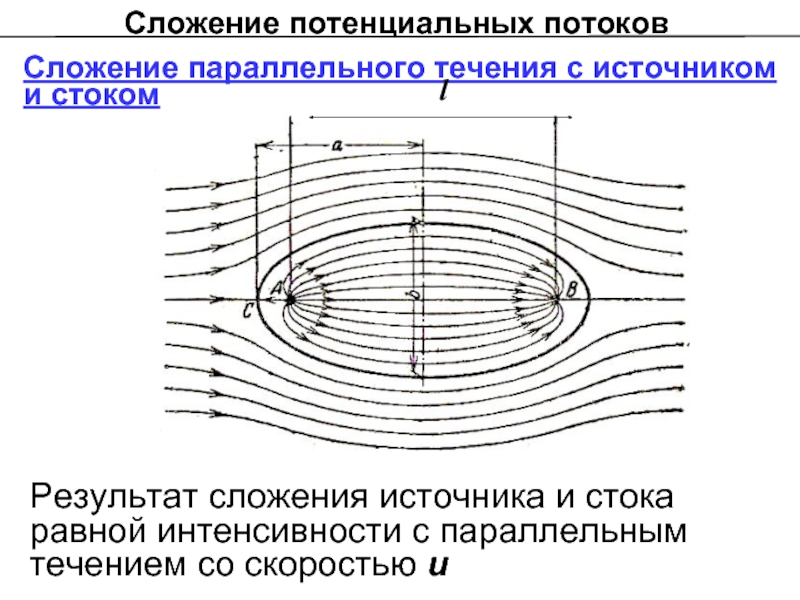
Сложение параллельного течения с источником и стоком
l
Результат сложения
Слайд 19Влево от точки А скорость с пары источника и стока направлена
Сложение потенциальных потоков
Paccтояние до этой критической точки от начала координат подсчитывается из уравнения
Слайд 20Сложение потенциальных потоков
Вторая критическая точка имеет абсциссу «-а».
В этих границах
Максимальную ширину тела можно подсчитать из условия, что между у=0 и у=b/2 секундная расход протекающей жидкости должен рав-
няться Q/2.
Слайд 21Сложение потенциальных потоков
Сложение источника и вихря
Это суммарное течение называют вихреисточ-ником,
Тогда скорости в точке
Поместим источник и вихрь в начало координат:
Слайд 22Сложение потенциальных потоков
Угол α величина постоянная и, как можно ви-деть, точка,
Тогда
Откуда после интегрирования и определения постоянной интегрирования получаем
Изопотенциальными линиями служат логариф-мические спирали
Слайд 23Сложение потенциальных потоков
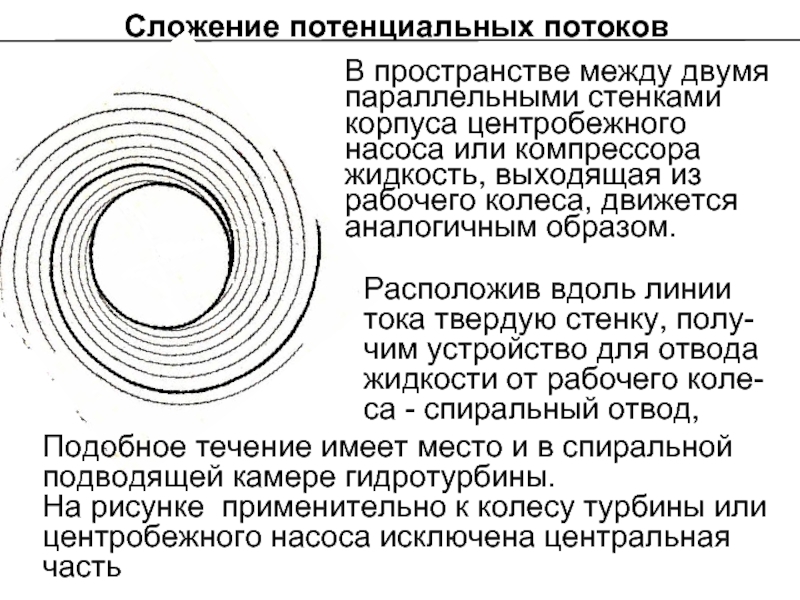
В пространстве между двумя параллельными стенками корпуса центробежного насоса
Расположив вдоль линии тока твердую стенку, полу-чим устройство для отвода жидкости от рабочего коле-са - спиральный отвод,
Подобное течение имеет место и в спиральной подводящей камере гидротурбины.
На рисунке применительно к колесу турбины или центробежного насоса исключена центральная часть