- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Сложение колебаний Сложение гармонических колебаний одного направления и одинаковой частоты презентация
Содержание
- 1. Сложение колебаний Сложение гармонических колебаний одного направления и одинаковой частоты
- 2. Сложение гармонических колебаний одного направления и одинаковой
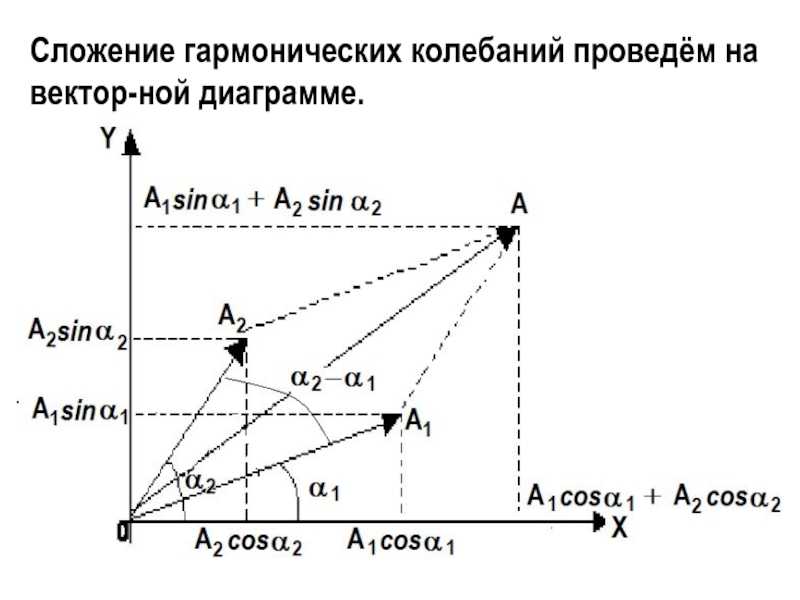
- 3. Сложение гармонических колебаний проведём на векторной диаграмме.
- 4. Результирующий вектор, определяемый по правилу параллелограмма, будет
- 5. Амплитуда результирующего колебания получается наибольшей (А =
- 6. При разности фаз складываемых колебаний кратной нечётному
- 7. При равенстве амплитуд А1 = A2 складываемых
- 8. БИЕНИЯ х1 = А1cos (ωt + ϕ1)
- 9. В результате сложения этих двух колебаний получаем
- 10. Биениями называют периодические изменения амплитуды результирующего колебания
- 11. Сложение перпендикулярных колебаний.
- 12. После необходимых математических преобразований (выразить косинус суммы
- 13. Частные случаи: а) ϕ = 0 (или
- 14. в) ϕ = π/2 - колебания по
- 15. Фигуры Лиссажу. Частоты взаимно - перпендикулярных колебаний
- 16. ЗАТУХАЮЩИЕ КОЛЕБАНИЯ
- 17. Сила трения (или сопротивления) где r –
- 18. Решение этого уравнения имеет вид (при
- 19. называется условным периодом затухающих колебаний
- 20. Найдем отношение значений амплитуды затухающих колебаний в
- 21. Натуральный логарифм отношения амплитуд, следующих друг за
- 22. Пусть N число колебаний, после которых амплитуда
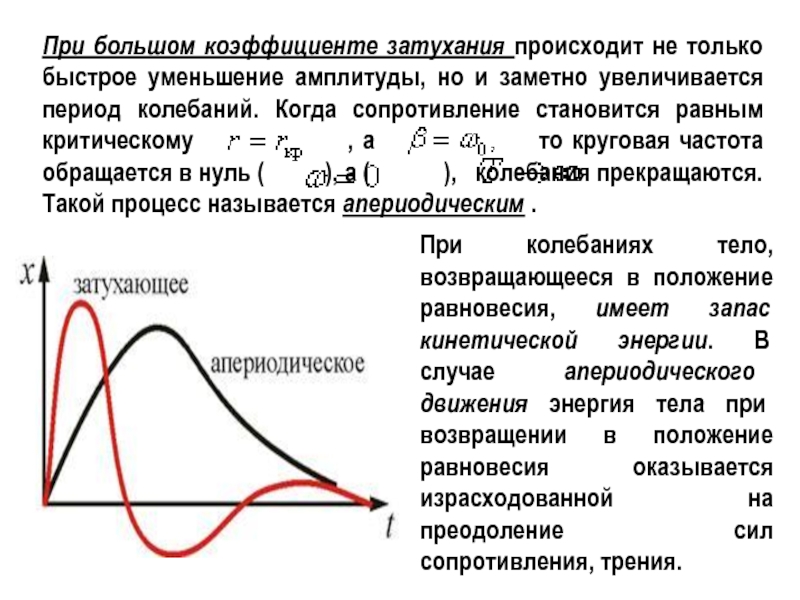
- 23. При большом коэффициенте затухания происходит не только
- 24. Для характеристики колебательной системы употребляется величина, называемая
- 25. Пружинный маятник Колебательный контур
- 26. При малых затуханиях можно считать, что энергия
- 27. Скорость убывания энергии со временем
- 28. При слабом затухании колебаний добротность с точностью
- 29. Контрольные вопросы Формулы амплитуды и начальной фазы
Слайд 2Сложение гармонических колебаний одного направления и одинаковой частоты:
х1 = А1
Результирующее колебание х = х1 + х2 должно быть гармоническим колебанием той же частоты ω, что и складываемые колебания, то есть х = А cos (ωt + ϕ). Задача заключается в нахождении амплитуды А и начальной фазы ϕ результирующего колебания.
Слайд 4Результирующий вектор, определяемый по правилу параллелограмма, будет изображать результирующее колебание х
Амплитуду А результирующего колебания определим из векторной диаграммы по теореме косинусов:
и начальную фазу ϕ из
Слайд 5Амплитуда результирующего колебания получается наибольшей (А = Амакс) при их синфазности,
Амакс = А1 + А2 при ϕ2 - ϕ1 = ± 2mπ;
Слайд 6При разности фаз складываемых колебаний кратной нечётному числу π они оказываются
Амин = А1 - А2 при ϕ2 - ϕ1 = ± (2m + 1)π; m = 0, 1, 2, …
Слайд 7При равенстве амплитуд А1 = A2 складываемых колебаний амплитуда результирующего колебания
Противофазные колебания с равными амплитудами полностью погашают друг друга.
Слайд 8БИЕНИЯ
х1 = А1cos (ωt + ϕ1)
х2 = А1cos (ω +
Результирующий вектор с амплитудой А = А1 + A2 будет при этом пульсировать по величине (по модулю) и вращаться с переменной скоростью.
Слайд 9В результате сложения этих двух колебаний получаем
х = Аcos ωt
Слайд 10Биениями называют периодические изменения амплитуды результирующего колебания от сложения двух однонаправленных
Слайд 11Сложение перпендикулярных колебаний.
Задача нахождения траектории результирующего движения заключается в исключении
Слайд 12После необходимых математических преобразований (выразить косинус суммы аргументов, найти чему равны
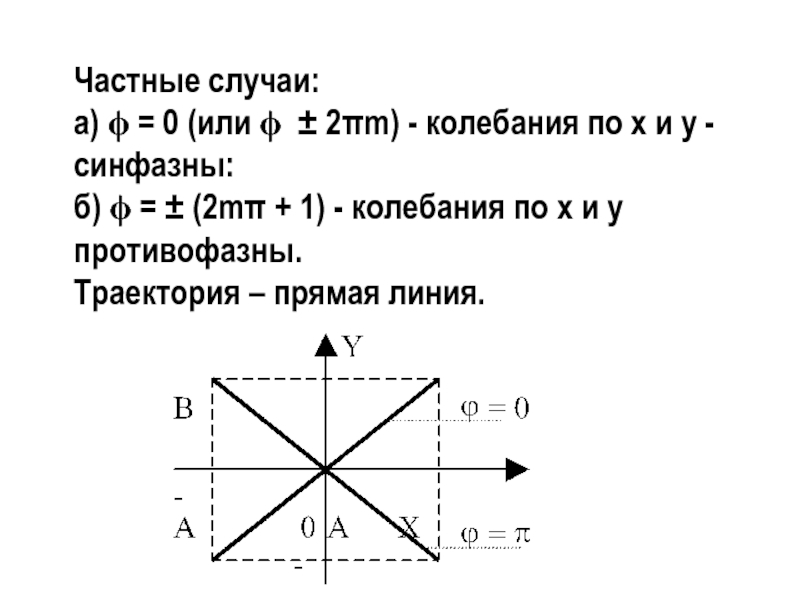
Слайд 13Частные случаи:
а) ϕ = 0 (или ϕ ± 2πm) - колебания
б) ϕ = ± (2mπ + 1) - колебания по х и у противофазны.
Траектория – прямая линия.
Слайд 14в) ϕ = π/2 - колебания по х и у фазно-ортогональны.
Уравнение траектории: х2/А2 + у2/В2 = 1 - уравнение эллипса приведённого к осям координат.
При равенстве амплитуд складываемых взаимно-перпендикулярных колебаний эллипс вырождается в окружность.
Случаи ϕ = π/2 и ϕ = - π/2 отличаются направлением движения точки по эллипсу или
окружности (по или
против часовой стрелки).
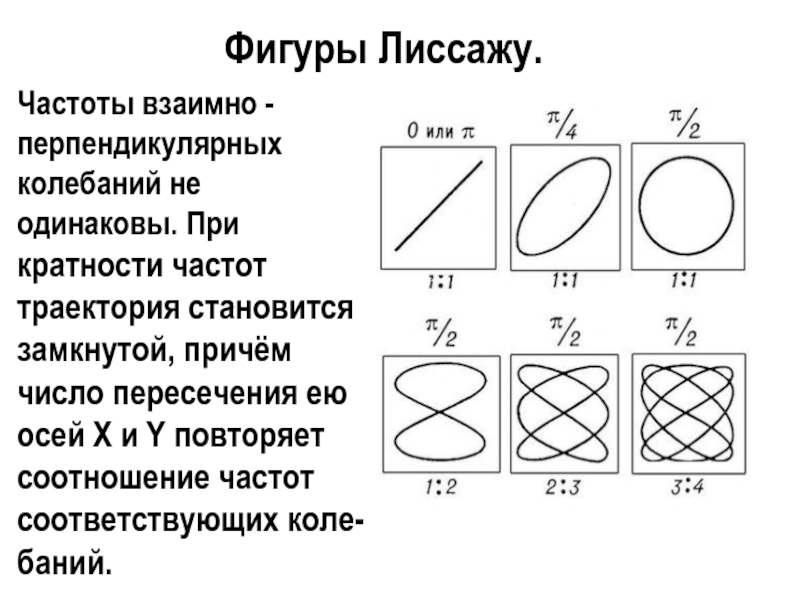
Слайд 15Фигуры Лиссажу.
Частоты взаимно - перпендикулярных колебаний не одинаковы. При кратности частот
Слайд 17Сила трения (или сопротивления)
где r – коэффициент сопротивления, – скорость
Запишем второй закон Ньютона для затухающих прямолинейных колебаний вдоль оси x:
где kx – возвращающая сила, rυx – сила трения. Разделим на массу и введем обозначения:
.
Получаем
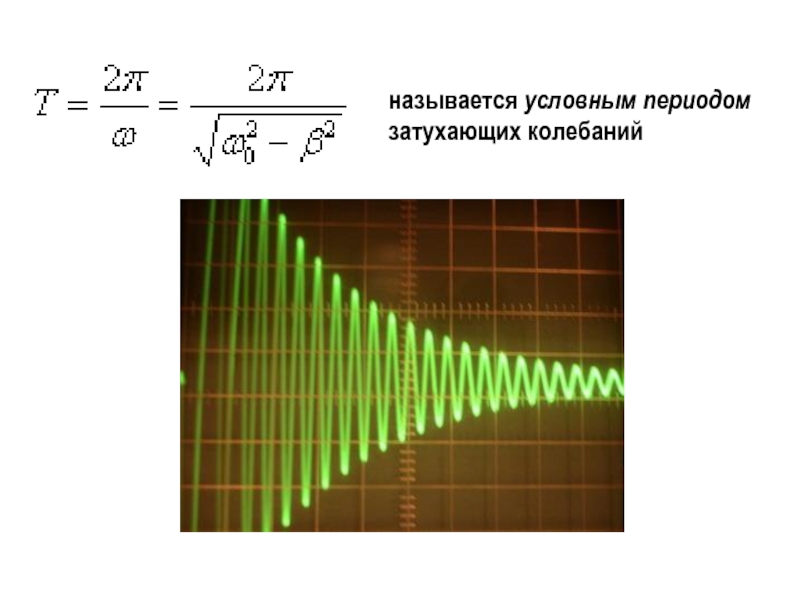
Слайд 18Решение этого уравнения имеет вид (при
где ω0 – круговая частота собственных колебаний (без затухания);
ω – круговая частота свободных затухающих колебаний.
Для колебаний под действием упругой силы
; ;
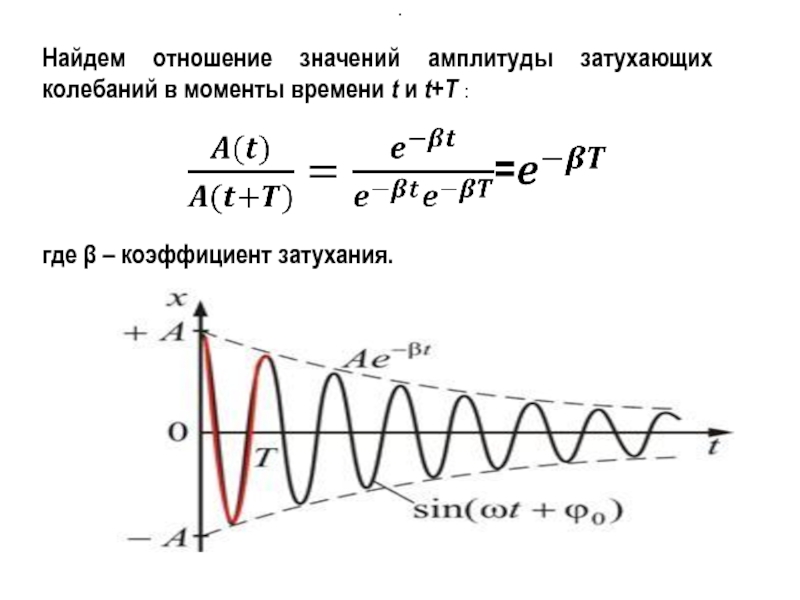
Слайд 20Найдем отношение значений амплитуды затухающих колебаний в моменты времени t и
где β – коэффициент затухания.
.
Слайд 21Натуральный логарифм отношения амплитуд, следующих друг за другом через период Т,
Время релаксации – время, в течение которого амплитуда А уменьшается в e раз.
отсюда
Слайд 22Пусть N число колебаний, после которых амплитуда уменьшается в e раз.
; ;
Итак, логарифмический декремент затухания есть физическая величина, обратная числу колебаний, по истечении которых амплитуда А уменьшается в e раз.
Слайд 23При большом коэффициенте затухания происходит не только быстрое уменьшение амплитуды, но
При колебаниях тело, возвращающееся в положение равновесия, имеет запас кинетической энергии. В случае апериодического движения энергия тела при возвращении в положение равновесия оказывается израсходованной на преодоление сил сопротивления, трения.
Слайд 24Для характеристики колебательной системы употребляется величина, называемая добротностью.
Добротность пропорциональна количеству колебаний,
Слайд 26При малых затуханиях можно считать, что энергия в колебательной системе изменяется
где
- значение энергии в начальный момент времени. Продифференцируем это выражение по времени:
Слайд 27Скорость убывания энергии со временем
Если за период энергия мало изменяется,
Слайд 28При слабом затухании колебаний добротность с точностью до множителя 2
Слайд 29Контрольные вопросы
Формулы амплитуды и начальной фазы результирующего колебания при сложении одинаково
Общая формула траектории взаимно перпендикулярных колебаний.
Дифференциальное уравнение затухающих колебаний и его решение.
Логарифмический декремент затухания.
Определение добротности и формулы для пружинного маятника и колебательного контура






![БИЕНИЯх1 = А1cos (ωt + ϕ1) х2 = А1cos (ω + Δω)t + ϕ2)], где](/img/tmb/2/127539/b7fd868981e76e2e8a10f57cc5cb037b-800x.jpg)