- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Сложение колебаний презентация
Содержание
- 1. Сложение колебаний
- 2. Сложение колебаний, направленных вдоль одной прямой. Биения.
- 3. Если
- 4. Периодические изменения амплитуды результирующего колебания при наложении
- 5. Сложение взаимно перпендикулярных колебаний. Фигуры Лиссажу. Вначале
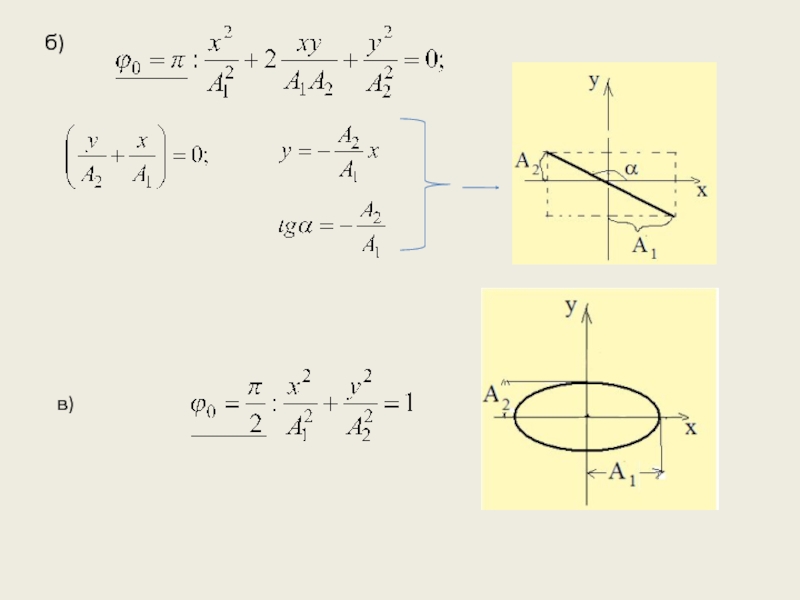
- 6. (1) Это уравнение эллипса, оси которого повернуты
- 7. б) в)
- 8. Рассмотрим случай близких частот, когда и
- 9. При сложении взаимно перпендикулярных гармонических колебаний характер
Слайд 15.4 СЛОЖЕНИЕ КОЛЕБАНИЙ
Часто периодический процесс описывается некой негармонической функцией
Метод разложения негармонической функции на гармонические составляющие называется разложением в ряд Фурье и является основным методом исследования в радиотехнике.
Слайд 2Сложение колебаний, направленных вдоль одной прямой. Биения.
Рассмотрим сложение двух гармонических колебаний
Результирующее колебание:
Слайд 3Если
Рассмотрим случай близких частот, когда
Пусть
Тогда:
Тогда разность фаз колебаний:
и
Слайд 4Периодические изменения амплитуды результирующего колебания при наложении двух гармонических колебаний одинакового
- период пульсаций амплитуды
- амплитуда биений
Биения возникают от того, что один из двух сигналов постоянно отстаёт от другого по фазе и в те моменты, когда колебания происходят синфазно, суммарный сигнал оказывается усилен, а в те моменты, когда два сигнала оказываются в противофазе, они взаимно гасят друг друга. Эти моменты периодически сменяют друг друга по мере того как нарастает отставание.
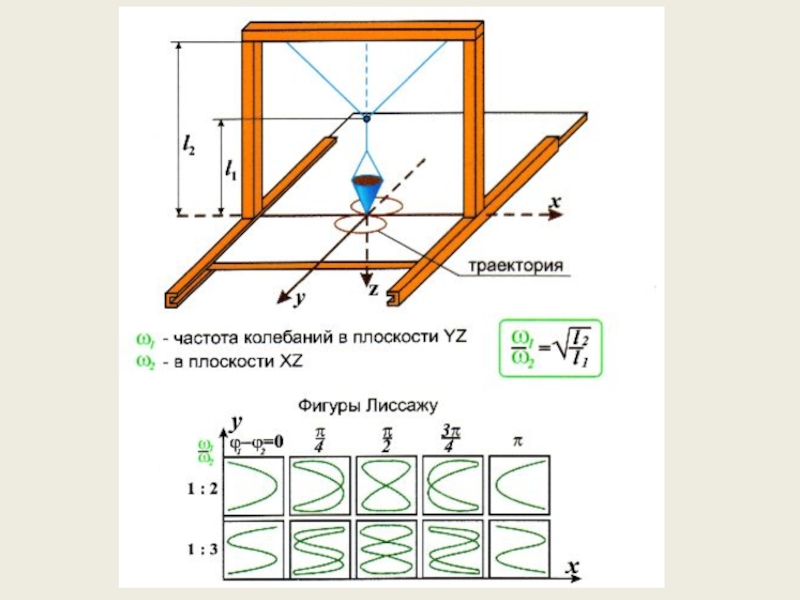
Слайд 5Сложение взаимно перпендикулярных колебаний.
Фигуры Лиссажу.
Вначале рассмотрим случай
Найдем траекторию движения м.т., колеблющейся
Слайд 6(1)
Это уравнение эллипса, оси которого повернуты относительно осей OX,OY.
Рассмотрим частные случаи.
а)
- траектория движения точки.
Слайд 8Рассмотрим случай близких частот, когда
и
- разность фаз складываемых колебаний медленно
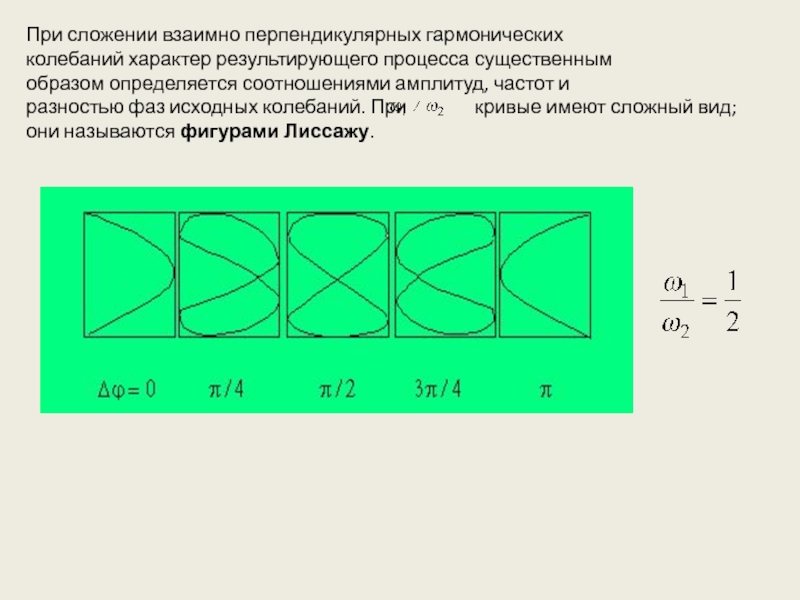
Слайд 9При сложении взаимно перпендикулярных гармонических
колебаний характер результирующего процесса существенным
образом определяется соотношениями
разностью фаз исходных колебаний. При кривые имеют сложный вид; они называются фигурами Лиссажу.