Сергей Петрович
ауд. 246 м.к
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Синтез зубчатых передач презентация
Содержание
- 1. Синтез зубчатых передач
- 2. Геометрический расчет ЗП, образованных из колес, нарезанных
- 3. Геометрический расчет ЗП, образованных из колес, нарезанных
- 4. Геометрический расчет ЗП, образованных из колес, нарезанных
- 5. Геометрический расчет ЗП, образованных из колес, нарезанных инструментальной рейкой.
- 6. Геометрический расчет ЗП, образованных из колес, нарезанных
- 7. Геометрический расчет ЗП, образованных из колес, нарезанных
- 8. Геометрический расчет ЗП, образованных из колес, нарезанных
- 9. Геометрический расчет ЗП, образованных из колес, нарезанных инструментальной рейкой.
- 10. Геометрический расчет ЗП, образованных из колес, нарезанных
- 11. Геометрический расчет ЗП, образованных из колес, нарезанных
- 12. Геометрический расчет ЗП, образованных из колес, нарезанных
- 13. Геометрический расчет ЗП, образованных из колес, нарезанных инструментальной рейкой.
- 14. Геометрический расчет ЗП, образованных из колес, нарезанных
- 15. Геометрический расчет ЗП, образованных из колес, нарезанных инструментальной рейкой. Радиус окружности вершин зубьев
- 16. Интерференция зубьев, нарезанных реечным инструментом. Интерференцией называется
- 17. Интерференция зубьев, нарезанных реечным инструментом. Установим условия,
- 18. Интерференция зубьев, нарезанных реечным инструментом. Интерференция будет
- 19. Интерференция зубьев, нарезанных реечным инструментом.
- 20. Интерференция зубьев, нарезанных реечным инструментом.
- 21. Качественные показатели зубчатого зацепления. Качественные показатели дают
- 22. Коэффициент торцевого перекрытия. Коэффициентом перекрытия называется величина
- 23. Коэффициент торцевого перекрытия.
- 24. Коэффициент торцевого перекрытия. Коэффициент перекрытия определяет величину
- 25. Коэффициент торцевого перекрытия. Геометрический коэффициент перекрытия – отношение дуги зацепления к окружному шагу:
- 26. Коэффициент торцевого перекрытия. Коэффициент торцевого перекрытия не
- 27. Удельные скольжения
- 28. Удельные скольжения Для оценки абразивного износа поверхности
- 29. Удельные скольжения
- 30. Геометрический коэффициент удельного давления Основной причиной выхода
- 31. Геометрический коэффициент удельного давления
- 32. Геометрический коэффициент удельного давления
- 33. Геометрический коэффициент удельного давления Геометрическим коэффициентом удельного
- 34. Блокирующий контур Блокирующим контуром называется совокупность линий,
- 35. Блокирующий контур 1 – коэффициент торцевого
- 36. Блокирующий контур 9 – линия Sa1=0,4 m;
Геометрический расчет ЗП, образованных из колес, нарезанных инструментальной рейкой. Зубчатые колеса, нарезанные инструментальной рейкой, могут образовывать три вида передач: Положительную передачу, когда коэффициент суммы смещений положителен: Отрицательную передачу, когда Нулевую
Слайд 1Теория механизмов и машин
Лекция 13
Синтез зубчатых передач.
Лектор: ассистент каф. 202
Светличный
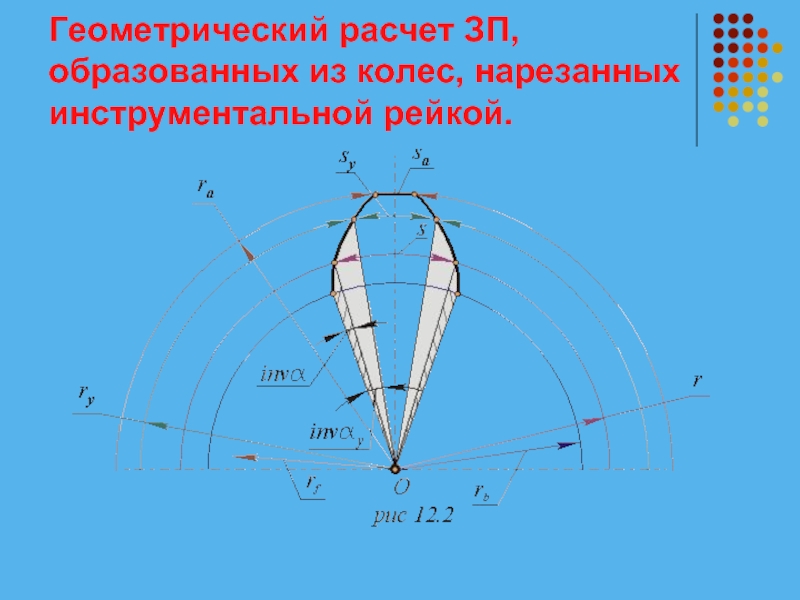
Слайд 2Геометрический расчет ЗП, образованных из колес, нарезанных инструментальной рейкой.
Зубчатые колеса, нарезанные
инструментальной рейкой, могут образовывать три вида передач:
Положительную передачу, когда коэффициент суммы смещений положителен:
Отрицательную передачу, когда
Нулевую передачу, когда
Положительную передачу, когда коэффициент суммы смещений положителен:
Отрицательную передачу, когда
Нулевую передачу, когда
Слайд 3Геометрический расчет ЗП, образованных из колес, нарезанных инструментальной рейкой.
Положительная передача может
состоять: из двух положительных колес; из одного положительного, а другого нулевого, из одного положительного, а другого отрицательного (если положительный коэффициент смещения по абсолютной величине больше отрицательного .
Слайд 4Геометрический расчет ЗП, образованных из колес, нарезанных инструментальной рейкой.
В отрицательную передачу
могут входить: два отрицательных колеса; одно отрицательное, а другое нулевое; одно отрицательное, а другое положительное (если отрицательный коэффициент смещения по абсолютной величине больше положительного).
Нулевая передача может быть образована парой нулевых колес или положительным и отрицательным колесом с равными коэффициентами смещения.
Нулевая передача может быть образована парой нулевых колес или положительным и отрицательным колесом с равными коэффициентами смещения.
Слайд 6Геометрический расчет ЗП, образованных из колес, нарезанных инструментальной рейкой.
Радиус делительной окружности
Радиус
основной окружности
Радиус окружности впадин
Радиус окружности впадин
Слайд 7Геометрический расчет ЗП, образованных из колес, нарезанных инструментальной рейкой.
Радиус окружности, проходящей
через граничную точку L:
Слайд 8Геометрический расчет ЗП, образованных из колес, нарезанных инструментальной рейкой.
Толщина зуба по
дуге делительной окружности.
Толщина зуба по дуге окружности произвольного радиуса ry
Толщина зуба по дуге окружности произвольного радиуса ry
Слайд 10Геометрический расчет ЗП, образованных из колес, нарезанных инструментальной рейкой.
Угол зацепления определен
из условия зацепления без боковых зазоров
Для положительной передачи: , для отрицательной передачи , для нулевой передачи
Для положительной передачи: , для отрицательной передачи , для нулевой передачи
Слайд 11Геометрический расчет ЗП, образованных из колес, нарезанных инструментальной рейкой.
Радиус начальной окружности
Межосевое
расстояние
Делительное межосевое расстояние нулевой передачи:
Делительное межосевое расстояние нулевой передачи:
Слайд 12Геометрический расчет ЗП, образованных из колес, нарезанных инструментальной рейкой.
Делительное межосевое расстояние
нулевой передачи:
При
Разность называется воспринимаемым смещением
При
Разность называется воспринимаемым смещением
Слайд 14Геометрический расчет ЗП, образованных из колес, нарезанных инструментальной рейкой.
Отношение воспринимаемого смещения
к модулю называется коэффициентом воспринимаемого смещения:
Величина на которую надо сблизить оси колес, чтобы устранить боковой зазор между зубьями, называется уравнительным смещением –
Коэффициент уравнительного смещения
Величина на которую надо сблизить оси колес, чтобы устранить боковой зазор между зубьями, называется уравнительным смещением –
Коэффициент уравнительного смещения
Слайд 15Геометрический расчет ЗП, образованных из колес, нарезанных инструментальной рейкой.
Радиус окружности вершин
зубьев
Слайд 16Интерференция зубьев, нарезанных реечным инструментом.
Интерференцией называется такое явление, когда часть пространства
оказывается одновременно занята двумя взаимодействующими зубьями. При этом траектория относительного движения точки, принадлежащей кромке зуба одного колеса, накладывается на переходную кривую другого.
В реальных условиях встреча кромки зуба одного колеса с переходной поверхностью зуба другого колеса приводит к заклиниванию зубчатой передачи.
В реальных условиях встреча кромки зуба одного колеса с переходной поверхностью зуба другого колеса приводит к заклиниванию зубчатой передачи.
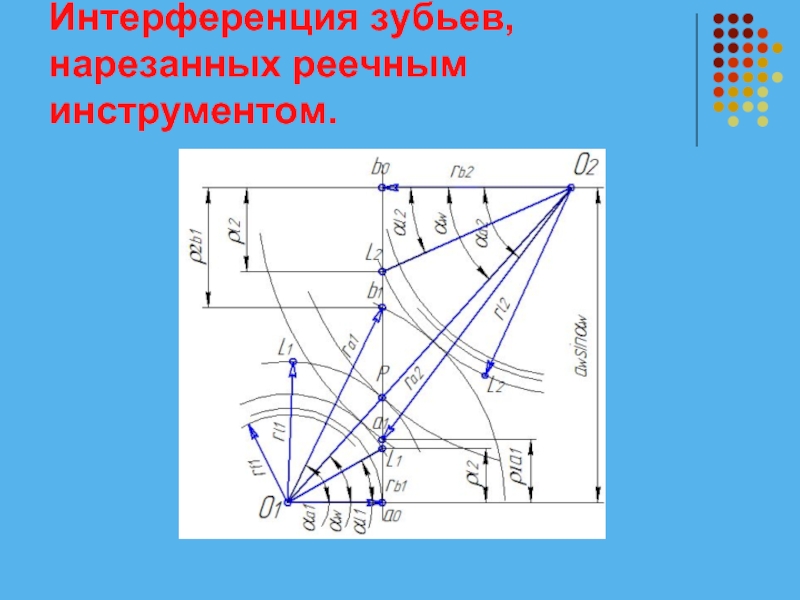
Слайд 17Интерференция зубьев, нарезанных реечным инструментом.
Установим условия, при соблюдении которых интерференции зубьев
не будет.
Участки профилей зубьев от точки а1 до окружности вершин первого колеса и от точки b1 до окружности вершин второго колеса являются активными профилями зубьев, а точки а1 и b1 – нижними точками активных профилей зубьев.
Участки профилей зубьев от точки а1 до окружности вершин первого колеса и от точки b1 до окружности вершин второго колеса являются активными профилями зубьев, а точки а1 и b1 – нижними точками активных профилей зубьев.
Слайд 18Интерференция зубьев, нарезанных реечным инструментом.
Интерференция будет отсутствовать, если:
где и
- радиусы кривизны профилей зубьев в граничных точках L1 и L2
Слайд 20Интерференция зубьев, нарезанных реечным инструментом.
и
- радиусы кривизны активных профилей зубьев в нижних точках.
Слайд 21Качественные показатели зубчатого зацепления.
Качественные показатели дают возможность произвести оценку передачи при
ее проектировании в отношении плавности и бесшумности зацепления, возможного износа и прочности зубьев колес.
К качественным показателям зацепления относятся: коэффициент торцевого перекрытия (εα), удельные скольжения профилей зубьев (υ1) и (υ2) , геометрический коэффициент удельного давления (ν).
К качественным показателям зацепления относятся: коэффициент торцевого перекрытия (εα), удельные скольжения профилей зубьев (υ1) и (υ2) , геометрический коэффициент удельного давления (ν).
Слайд 22Коэффициент торцевого перекрытия.
Коэффициентом перекрытия называется величина отношения угла перекрытия зубчатого колеса
к его угловому шагу, где под углом перекрытия понимают угол, на который поворачивается колесо за время зацепления одной пары зубьев
Слайд 24Коэффициент торцевого перекрытия.
Коэффициент перекрытия определяет величину зоны двухпарного контакта, когда одновременно
зацепляются два последовательно расположенных зуба.
Коэффициент перекрытия влияет на плавность работы и безударность.
Коэффициент торцевого перекрытия должен быть больше единицы, с тем, чтобы вторая пара взаимодействующих зубьев успела войти в зацепление, прежде чем первая пара выйдет из зацепления.
Коэффициент перекрытия влияет на плавность работы и безударность.
Коэффициент торцевого перекрытия должен быть больше единицы, с тем, чтобы вторая пара взаимодействующих зубьев успела войти в зацепление, прежде чем первая пара выйдет из зацепления.
Слайд 25Коэффициент торцевого перекрытия.
Геометрический коэффициент перекрытия – отношение дуги зацепления к окружному
шагу:
Слайд 26Коэффициент торцевого перекрытия.
Коэффициент торцевого перекрытия не зависит от модуля, увеличивается при
увеличении чисел зубьев z1 и z2 и уменьшается при увеличении αw.
Для прямозубого внешнего зацепления
Для прямозубого внешнего зацепления
Слайд 28Удельные скольжения
Для оценки абразивного износа поверхности зуба принято удельное скольжение –
отношение скорости скольжения к скорости перемещения точки контакта по поверхности зуба.
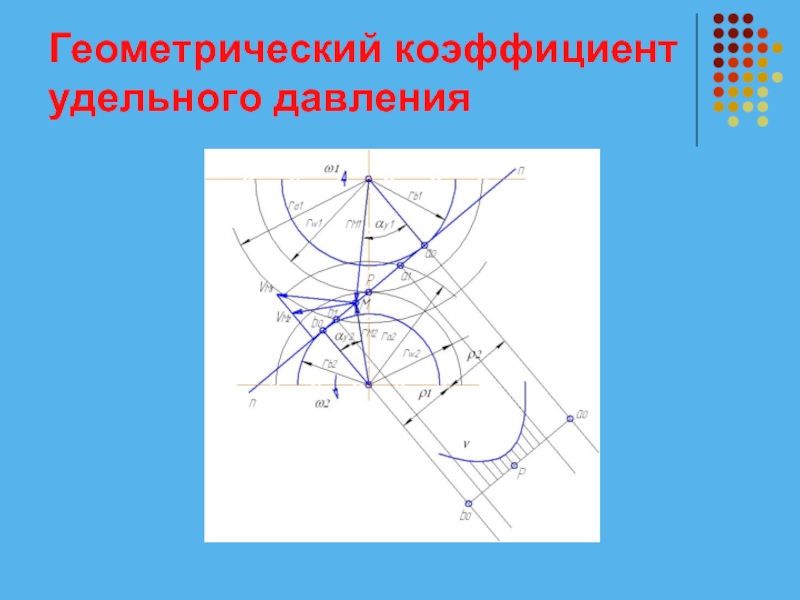
Слайд 30Геометрический коэффициент удельного давления
Основной причиной выхода из строя закрытых, хорошо смазанных
передач является усталостное выкрашивание рабочих поверхностей зубьев, вызываемое переменными контактными напряжениями.
Если принять эвольвентные поверхности на отдельных участках зубьев за поверхности круговых цилиндров, радиусы которых равны радиусам кривизны эвольвентных поверхностей в точках их контакта, то максимальное контактное напряжение можно определить по формуле Герца:
Если принять эвольвентные поверхности на отдельных участках зубьев за поверхности круговых цилиндров, радиусы которых равны радиусам кривизны эвольвентных поверхностей в точках их контакта, то максимальное контактное напряжение можно определить по формуле Герца:
Слайд 31Геометрический коэффициент удельного давления
где Рп – нормальное давление на
зубьях;
- приведенный модуль упругости
материала зубчатых колес;
b – ширина обода колеса; - величина,
обратная приведенному радиусу кривизны (знак минус для внутреннего зацепления).
- приведенный модуль упругости
материала зубчатых колес;
b – ширина обода колеса; - величина,
обратная приведенному радиусу кривизны (знак минус для внутреннего зацепления).
Слайд 33Геометрический коэффициент удельного давления
Геометрическим коэффициентом удельного давления называется отношение модуля к
приведенному радиусу кривизны:
Слайд 34Блокирующий контур
Блокирующим контуром называется совокупность линий, построенных в системе координат х2
и х1 для определенной зубчатой пары и ограничивающих область допустимых значений коэффициентов смещения.
Слайд 35Блокирующий контур
1 – коэффициент торцевого перекрытия εα =1;
2 – толщина зуба
колеса z1 по окружности вершин Sa1=0;
3 - допустимое подрезание колеса z2;
4 - допустимое подрезание колеса z1;
5 – интерференция или заклинивание с переходной кривой колеса z2;
6 – линия Sa2=0,25 m;
7 - линия Sa2=0,4 m;
8 – линия выравненных удельных скольжений;
3 - допустимое подрезание колеса z2;
4 - допустимое подрезание колеса z1;
5 – интерференция или заклинивание с переходной кривой колеса z2;
6 – линия Sa2=0,25 m;
7 - линия Sa2=0,4 m;
8 – линия выравненных удельных скольжений;
Слайд 36Блокирующий контур
9 – линия Sa1=0,4 m;
10 – линия Sa1=0,25 m;
11 –
линия x2=x2min;
12 – линия x1=x1min;
13 – линия εα =1,2
12 – линия x1=x1min;
13 – линия εα =1,2
