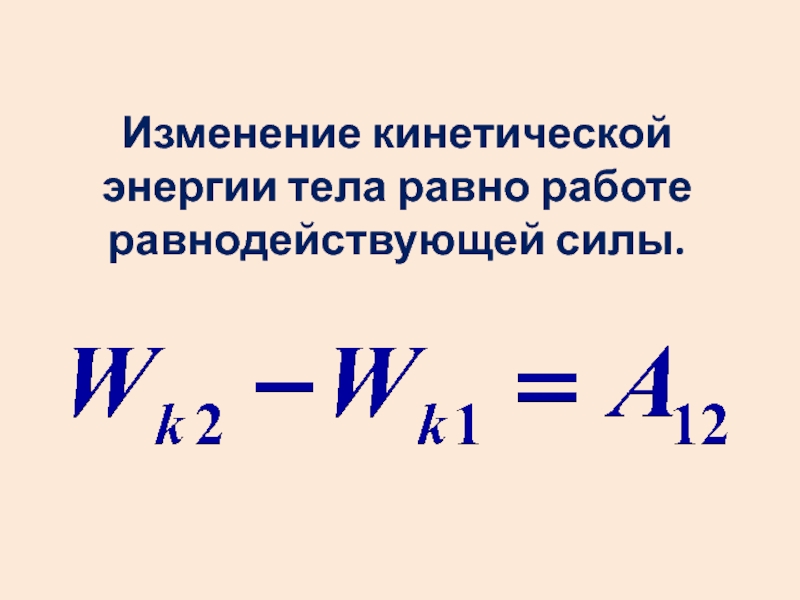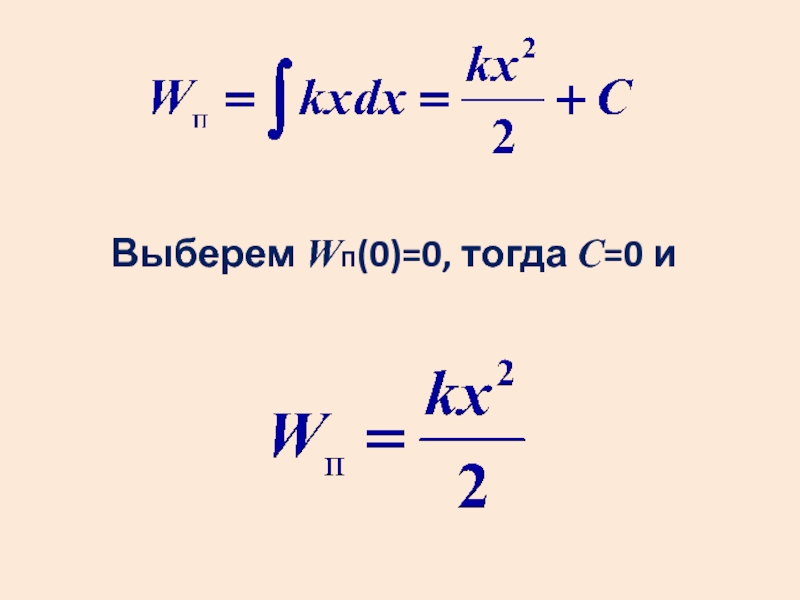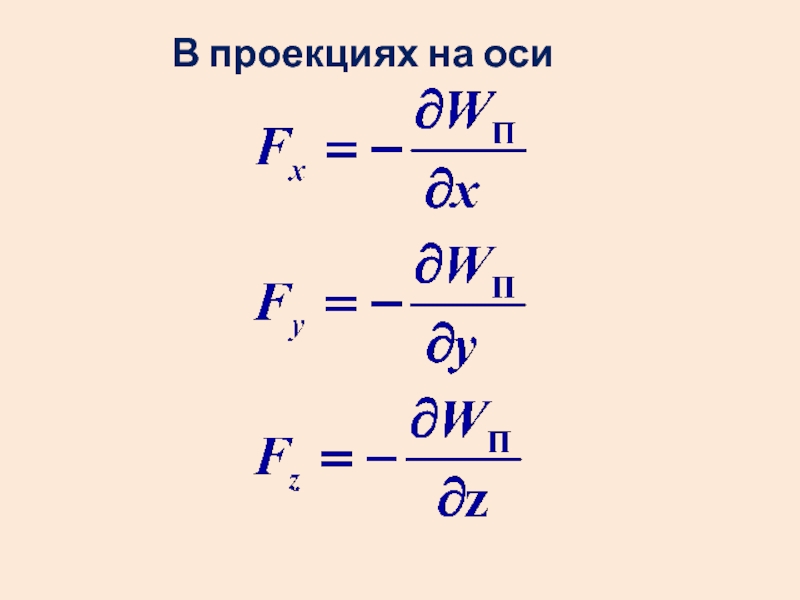системы и передающая действие одних частиц на другие.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Силовое поле. Работа. Энергия. Мощность презентация
Содержание
- 1. Силовое поле. Работа. Энергия. Мощность
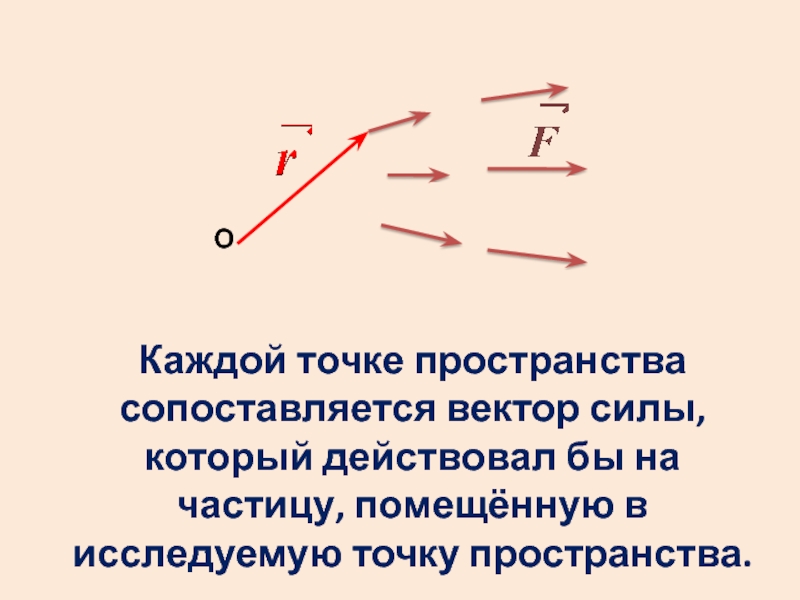
- 2. Каждой точке пространства сопоставляется вектор силы, который
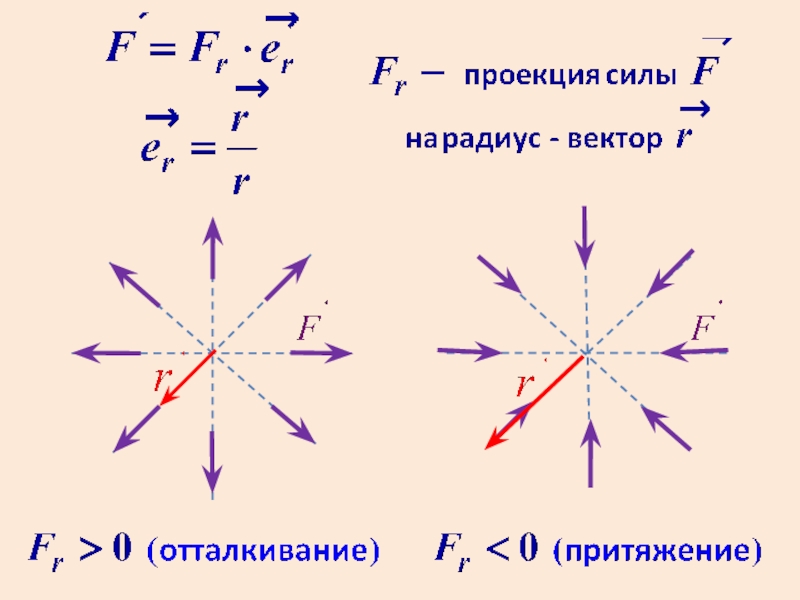
- 3. Центральное силовое поле В поле центральных сил
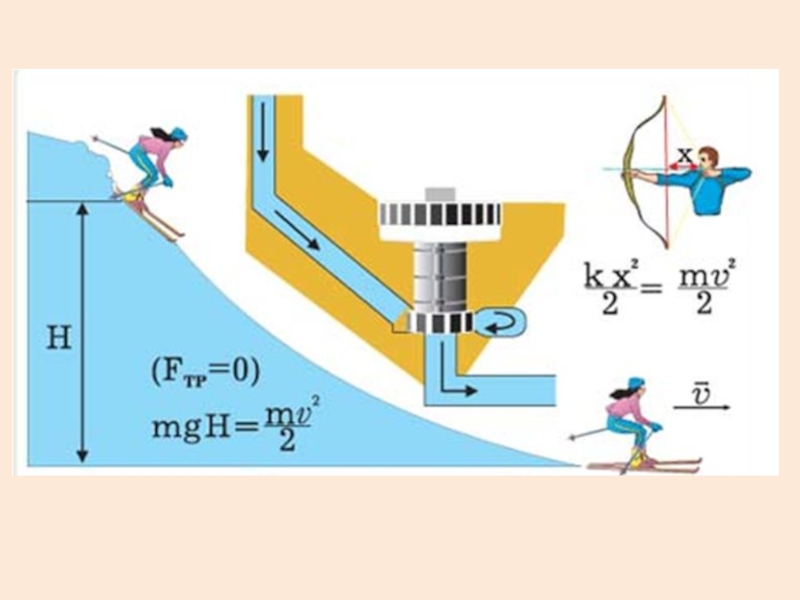
- 5. Примеры центральных сил: Силы тяготения в гравитационном
- 6. Однородное силовое поле В однородном силовом поле
- 7. ЭНЕРГИЯ Энергия – общая мера различных
- 8. РАБОТА СИЛ ПОЛЯ При превращении одной формы
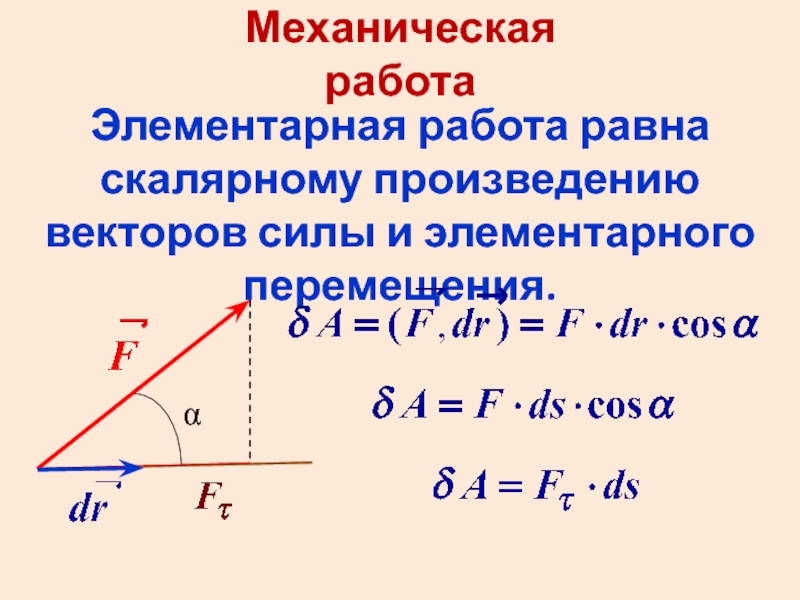
- 9. Механическая работа Элементарная работа равна скалярному произведению
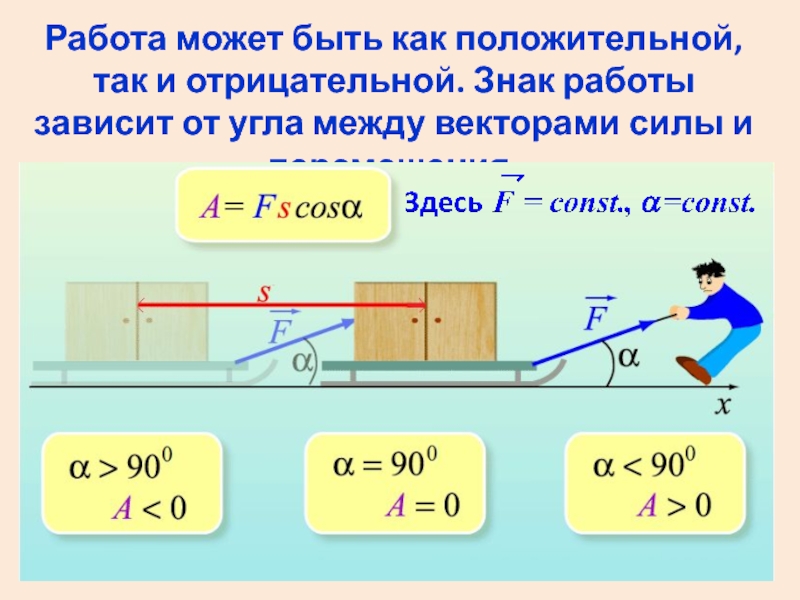
- 10. Работа может быть как положительной, так и
- 11. Полная работа переменной силы:
- 12. Полная работа постоянной силы:
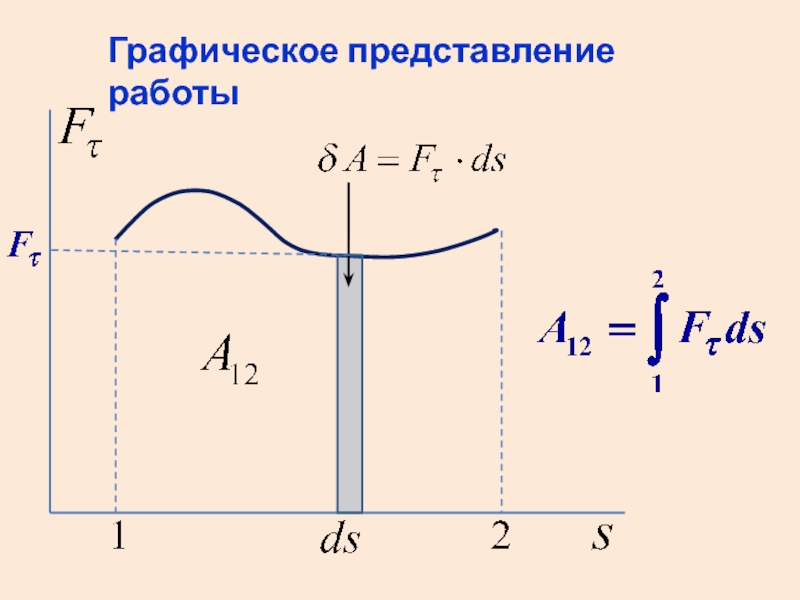
- 13. Графическое представление работы
- 14. Мощность Мощность равна работе, совершаемой в единицу времени.
- 15. Потенциальные силовые поля Силовое поле называют потенциальным,
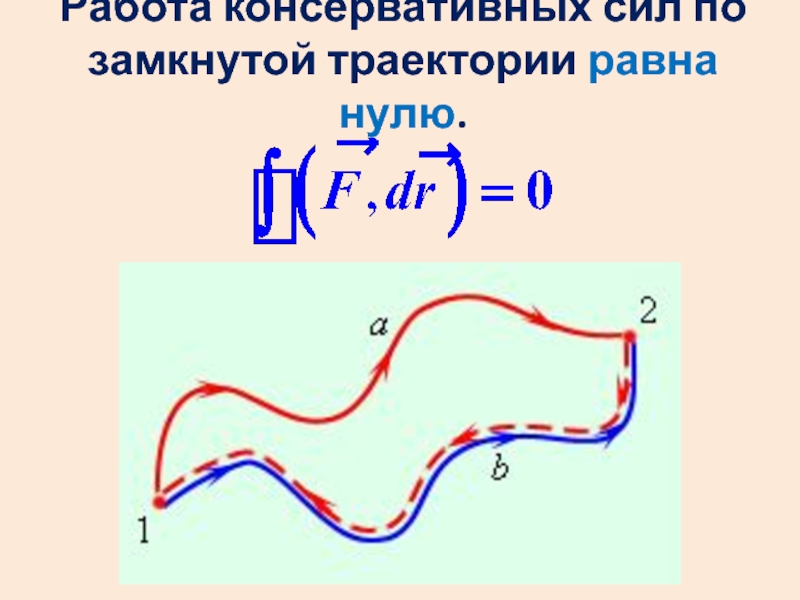
- 16. Работа консервативных сил по замкнутой траектории равна нулю. .
- 17. Примеры консервативных сил: Силы тяготения Упругие
- 18. Диссипативные силы Силы, работа которых зависит от
- 19. Работа диссипативных сил отрицательна. Работа этих сил по замкнутой траектории не равна нулю.
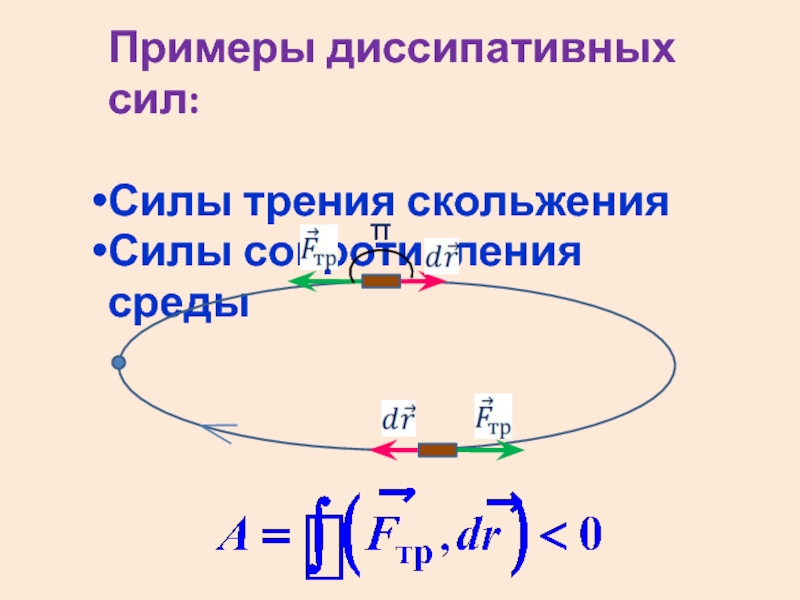
- 20. Примеры диссипативных сил: Силы трения скольжения
- 21. Кинетическая энергия Энергию, которой обладают движущиеся тела,
- 22. Пусть на МТ действует сила. Найдем ее работу.
- 23. Работа равна приращению величины в скобках. Это кинетическая энергия.
- 24. Изменение кинетической энергии тела равно работе равнодействующей силы.
- 25. Потенциальная энергия Потенциальная энергия – это энергия взаимодействия тел. Обозначим: WП.
- 26. Потенциальная энергия тела в силовом поле
- 27. При
- 28. Потенциальная энергия тела в поле силы
- 29. Выберем Тогда
- 30. Потенциальная энергия упругих сил По закону Гука
- 31. Выберем WП(0)=0, тогда С=0 и
- 32. Связь силы и потенциальной энергии Градиент скалярного
- 33. Поверхностью уровня скалярного поля называют совокупность точек
- 34. Вектор градиента скалярного поля:
- 35. Градиент скалярного поля – это вектор,
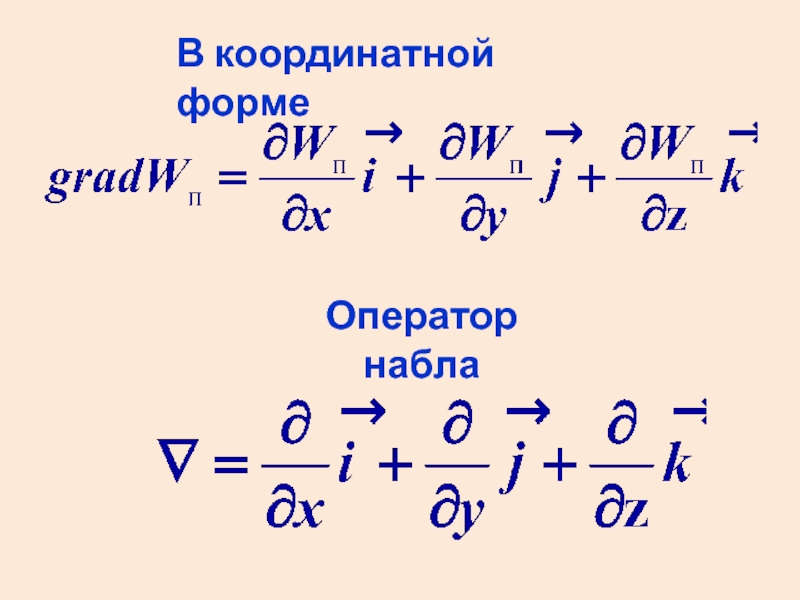
- 36. В координатной форме Оператор набла
- 37. Связь консервативной силы и потенциальной энергии или
- 38. В проекциях на оси
- 39. Потенциальная энергия взаимодействия системы тел Потенциальная
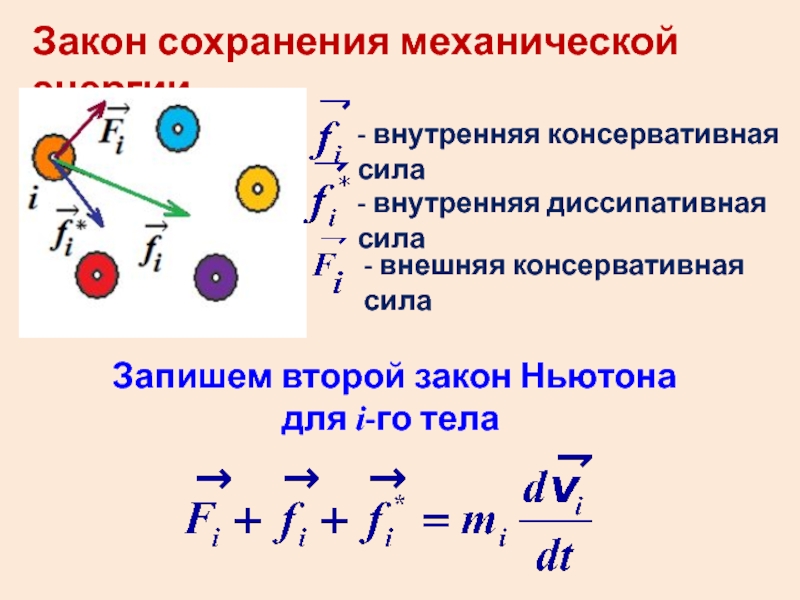
- 40. Закон сохранения механической энергии - внутренняя консервативная
- 41. Умножим скалярно обе части равенства на перемещение
- 42. Работа сил внешнего потенциального поля
- 43. Полная механическая энергия системы тел:
- 44. Закон изменения механической энергии системы тел Изменение механической энергии системы тел равно работе диссипативных сил.
- 45. Закон сохранения механической энергии системы тел В
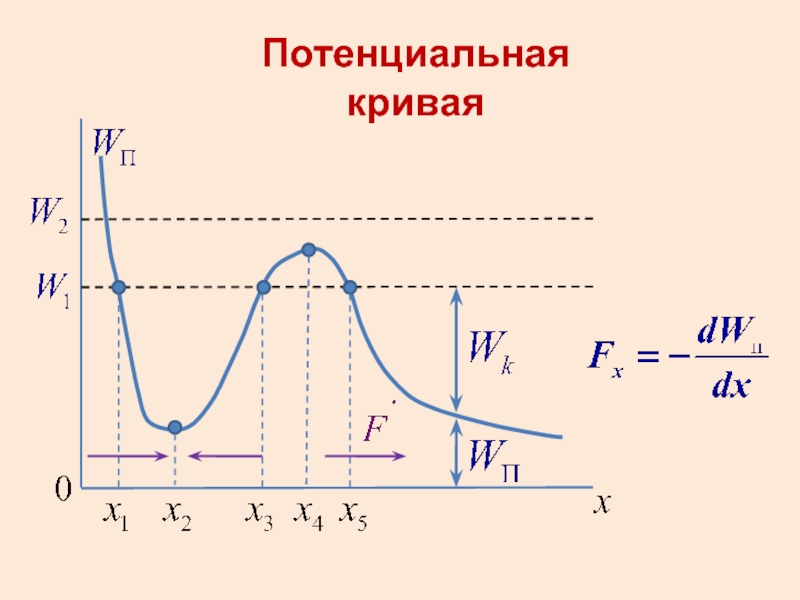
- 47. Потенциальная кривая
- 48. При соударении тел их взаимодействие длится очень
- 49. При ударе систему тел можно считать квазизамкнутой.
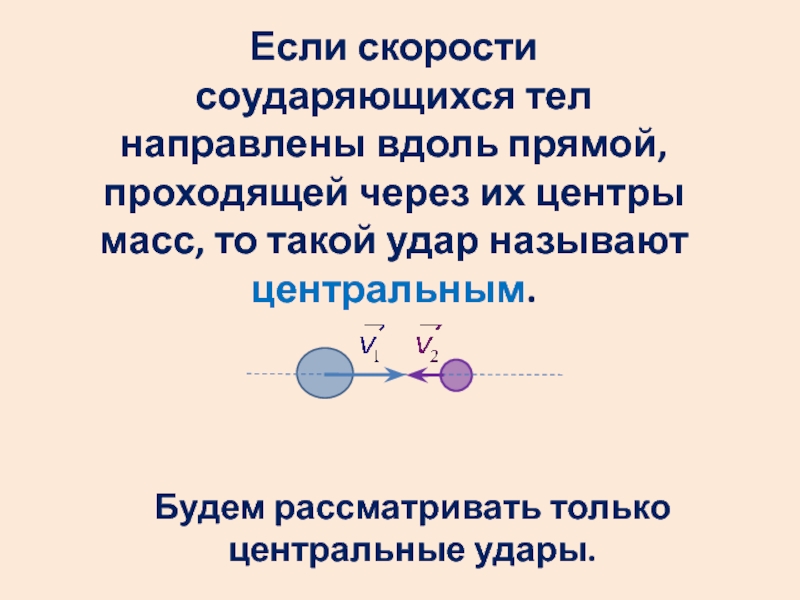
- 50. Если скорости соударяющихся тел направлены вдоль прямой,
- 51. Если при ударе не происходит перехода энергии
- 52. Если при ударе тела слипаются и движутся
- 53. Если тело налетает на неподвижную преграду, то
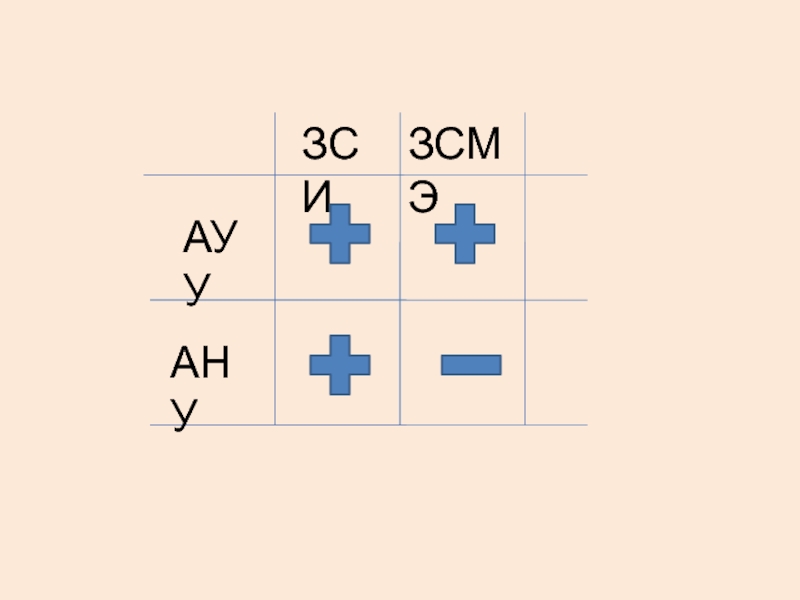
- 54. АУУ АНУ ЗСИ ЗСМЭ
- 55. Расчет скоростей тел после удара 1) Абсолютно упругий удар
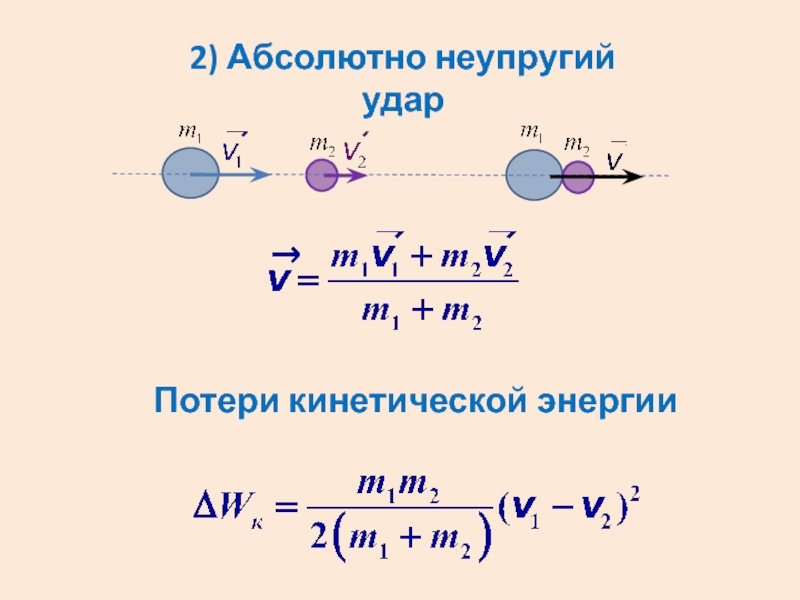
- 56. 2) Абсолютно неупругий удар Потери кинетической энергии
Каждой точке пространства сопоставляется вектор силы, который действовал бы на частицу, помещённую в исследуемую точку пространства. О
Слайд 2Каждой точке пространства сопоставляется вектор силы, который действовал бы на частицу,
помещённую в исследуемую точку пространства.
О
Слайд 3Центральное силовое поле
В поле центральных сил на МТ действуют силы, которые
направлены вдоль прямых, проходящих через одну и ту же точку – центр сил.
Величина этих сил зависит
только от расстояния до центра сил.
Величина этих сил зависит
только от расстояния до центра сил.
Слайд 5Примеры центральных сил:
Силы тяготения в гравитационном поле Земли
Упругие силы
Кулоновские силы, создаваемые
точечными зарядами
Слайд 6Однородное силовое поле
В однородном силовом поле вектор силы
одинаков в каждой
точке поля.
Пример: поле силы тяжести вблизи поверхности Земли.
Слайд 7ЭНЕРГИЯ
Энергия – общая мера различных форм движения материи.
В механике это перемещение
тел в пространстве и силовое взаимодействие между телами.
Им соответствуют кинетическая и потенциальная энергии.
Им соответствуют кинетическая и потенциальная энергии.
Слайд 8РАБОТА СИЛ ПОЛЯ
При превращении одной формы движения в другую совершается работа,
равная величине перехода энергии от одного вида к другому.
Слайд 9Механическая работа
Элементарная работа равна скалярному произведению векторов силы и элементарного перемещения.
α
Слайд 10Работа может быть как положительной, так и отрицательной. Знак работы зависит
от угла между векторами силы и перемещения.
Слайд 15Потенциальные силовые поля
Силовое поле называют потенциальным, а силы, действующие в нём,
консервативными, если работа сил поля не зависит от вида траектории, а зависит только от положений тела в исходном и конечном состояниях.
Слайд 17Примеры консервативных сил:
Силы тяготения
Упругие силы
Кулоновские силы
Все центральные силовые поля потенциальны.
Слайд 18Диссипативные силы
Силы, работа которых зависит от траектории движения, не являются консервативными.
Если при действии таких сил энергия переходит в немеханические формы, то эти силы называют диссипативными.
Слайд 19Работа диссипативных сил отрицательна.
Работа этих сил по замкнутой траектории не равна
нулю.
Слайд 21Кинетическая энергия
Энергию, которой обладают движущиеся тела, называют кинетической .
Обозначим: Wk.
Слайд 26Потенциальная энергия
тела в силовом поле
Силы поля, перемещая тело, совершают работу,
равную убыли потенциальной энергии:
Слайд 32Связь силы и потенциальной энергии
Градиент скалярного поля
Скалярным полем называют область пространства,
каждая точка которого характеризуется некоторой скалярной величиной, например, потенциальной энергией.
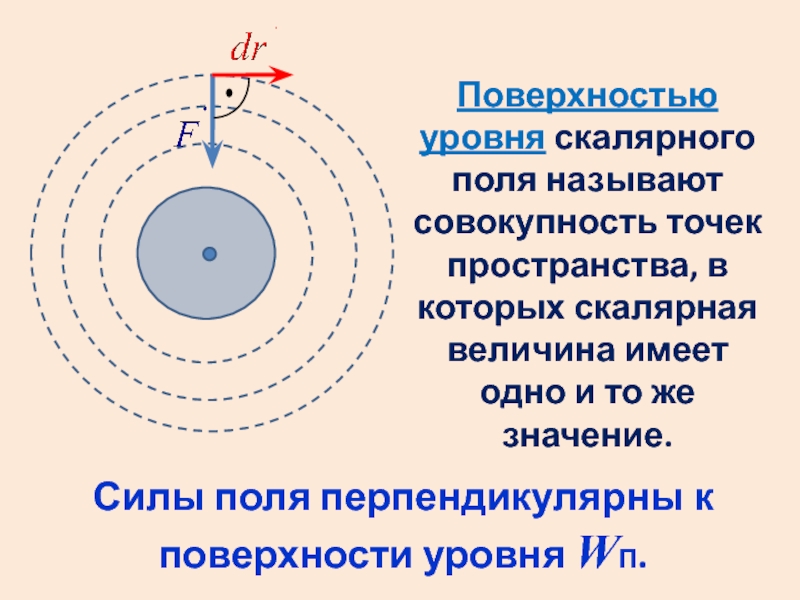
Слайд 33Поверхностью уровня скалярного поля называют совокупность точек пространства, в которых скалярная
величина имеет одно и то же значение.
Силы поля перпендикулярны к поверхности уровня WП.
Слайд 35Градиент скалярного поля
– это вектор, по модулю равный изменению скалярной
величины на единицу длины в направлении нормали к поверхности уровня.
Направлен вектор градиента перпендикулярно поверхности уровня в сторону возрастания этой скалярной величины.
Направлен вектор градиента перпендикулярно поверхности уровня в сторону возрастания этой скалярной величины.
Слайд 39Потенциальная энергия
взаимодействия системы тел
Потенциальная энергия взаимодействия – это величина, равная работе,
совершаемой силами взаимодействия тел при изменении расположения тел из данного состояния в состояние, в котором потенциальная энергия взаимодействия условно принимается равной нулю.
Слайд 40Закон сохранения механической энергии
- внутренняя консервативная сила
- внутренняя диссипативная сила
- внешняя
консервативная сила
Запишем второй закон Ньютона для i-го тела
Слайд 42
Работа сил внешнего потенциального поля
Работа сил
взаимодействия
Работа дисси-пативных сил
Изменение кинетической энергии
Слайд 44Закон изменения механической энергии системы тел
Изменение механической энергии системы тел равно
работе диссипативных сил.
Слайд 45Закон сохранения механической энергии системы тел
В системе, на тела которой действуют
только консервативные силы, механическая энергия не изменяется.
Слайд 48При соударении тел их взаимодействие длится очень короткое время. Поэтому силы
взаимодействия тел
велики, и внешними силами часто можно пренебречь.
велики, и внешними силами часто можно пренебречь.
Соударение тел
Слайд 49При ударе систему тел можно считать квазизамкнутой.
В такой системе тел
выполняется закон сохранения импульса.
Слайд 50Если скорости соударяющихся тел направлены вдоль прямой, проходящей через их центры
масс, то такой удар называют центральным.
Будем рассматривать только центральные удары.
Слайд 51Если при ударе не происходит перехода энергии в немеханические формы (ε=1),
то такой удар называют абсолютно упругим.
В этом случае выполняется закон сохранения механической энергии.
В этом случае выполняется закон сохранения механической энергии.
Виды удара
Слайд 52Если при ударе тела слипаются и движутся дальше как единое целое
(ε=0), то такой удар называют
абсолютно неупругим.
В этом случае механическая энергия полностью или частично переходит в немеханическую форму.
абсолютно неупругим.
В этом случае механическая энергия полностью или частично переходит в немеханическую форму.
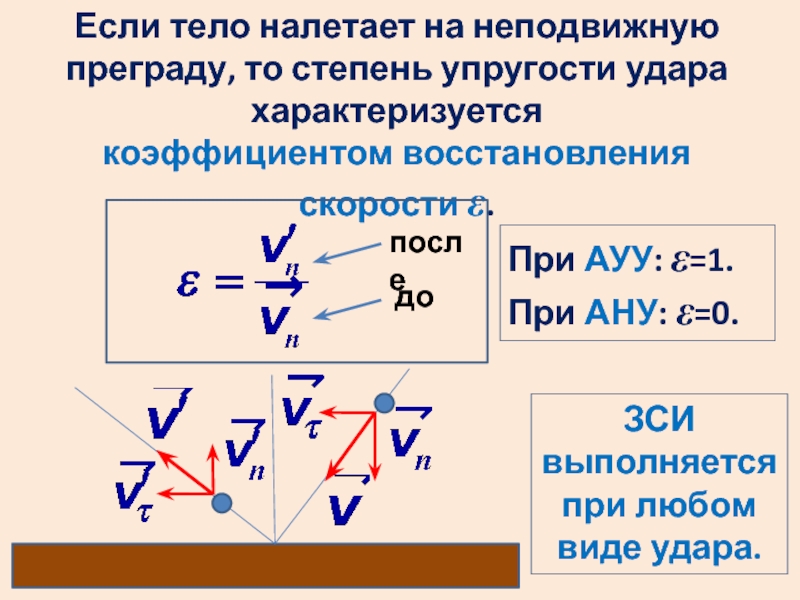
Слайд 53Если тело налетает на неподвижную преграду, то степень упругости удара характеризуется
коэффициентом восстановления скорости ε.
после
до
При АУУ: ε=1.
При АНУ: ε=0.
ЗСИ выполняется при любом виде удара.
