- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Сила инерции в прямолинейно движущейся НИСО презентация
Содержание
- 1. Сила инерции в прямолинейно движущейся НИСО
- 2. При учете сил инерции второй закон Ньютона
- 3. Силы инерции обусловлены ускоренным движением системы
- 4. Силы инерции при ускоренном поступательном движении
- 5. F=mgtgα=ma0 т. е. угол отклонения
- 6. Силы инерции, действующие на тело, покоящееся во
- 7. В инерциальной системе отсчета, которая связана, например,
- 8. Центробежные силы инерции
- 11. Центробежная сила инерции. Сила, приложенная к
- 12. Центробежная сила – сила инерции первого рода.
- 13. В неинерциальной системе (рис.1) R
- 14. Сила Кориолиса
- 15. Сила Кориолиса. При движении тела относительно вращающейся
- 16. Появление кориолисовой силы можно обнаружить
- 17. Чтобы заставить шарик катиться вдоль ОА, нужно
- 18. Ускорение направлено перпендикулярно векторам
- 19. Влияние кориолисовых сил необходимо учитывать
- 20. Силы Кориолиса проявляются и при качаниях
- 21. Если тело удаляется от оси
- 22. Маятник Фуко
- 23. Ма́ятник Фуко́ — маятник, используемый для экспериментальной демонстрации суточного
- 24. Маятник Фуко является математическим маятником, плоскость колебаний
Слайд 2При учете сил инерции второй закон Ньютона будет справедлив для любой
системы отсчета: произведение массы тела на ускорение в рассматриваемой системе отсчета равно сумме всех сил, действующих на данное тело (учитывая и силы инерции). При этом силы инерции Fin должны быть такими, чтобы вместе с силами F, обусловленными воздействием тел друг на друга, они сообщали телу ускорение а', каким оно обладает в неинерциальных системах отсчета, т. е.
Так как F=ma (a - ускорение тела в инерциальной системе отсчета), то
Так как F=ma (a - ускорение тела в инерциальной системе отсчета), то
Слайд 3
Силы инерции обусловлены ускоренным движением системы отсчета относительно измеряемой системы, поэтому
в общем случае следует учитывать следующие случаи возниконовения этих сил: 1) силы инерции при ускоренном поступательном движении системы отсчета; 2) силы инерции, которые действуют на тело, покоящееся во вращающейся системе отсчета; 3) силы инерции, которые действуют на тело, движущееся во вращающейся системе отсчета.
Рассмотрим эти случаи.
Рассмотрим эти случаи.
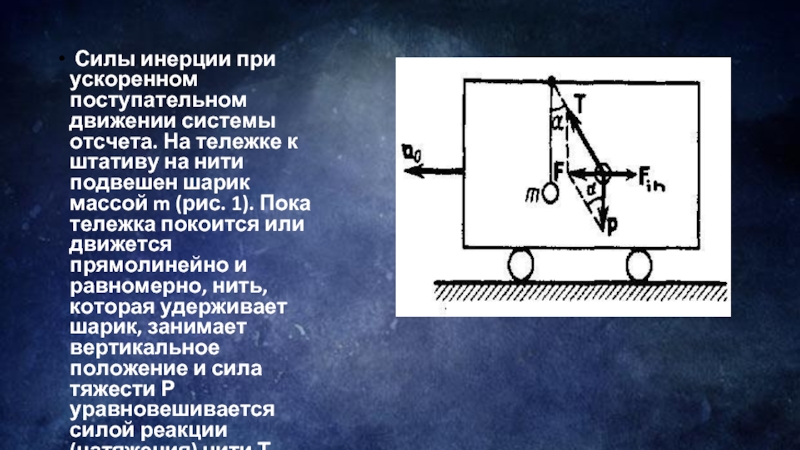
Слайд 4 Силы инерции при ускоренном поступательном движении системы отсчета. На тележке
к штативу на нити подвешен шарик массой m (рис. 1). Пока тележка покоится или движется прямолинейно и равномерно, нить, которая удерживает шарик, занимает вертикальное положение и сила тяжести Р уравновешивается силой реакции (натяжения) нити Т.
Слайд 5F=mgtgα=ma0
т. е. угол отклонения нити от вертикали тем больше, чем больше
ускорение тележки.
В системе отсчета, которая связана с ускоренно движущейся тележкой, шарик покоится, что возможно, если сила F уравновешивается равной и противоположно направленной ей силой Fin, которая является ничем иным, как силой инерции, так как на шарик никакие другие силы не действуют. Таким образом,
В системе отсчета, которая связана с ускоренно движущейся тележкой, шарик покоится, что возможно, если сила F уравновешивается равной и противоположно направленной ей силой Fin, которая является ничем иным, как силой инерции, так как на шарик никакие другие силы не действуют. Таким образом,
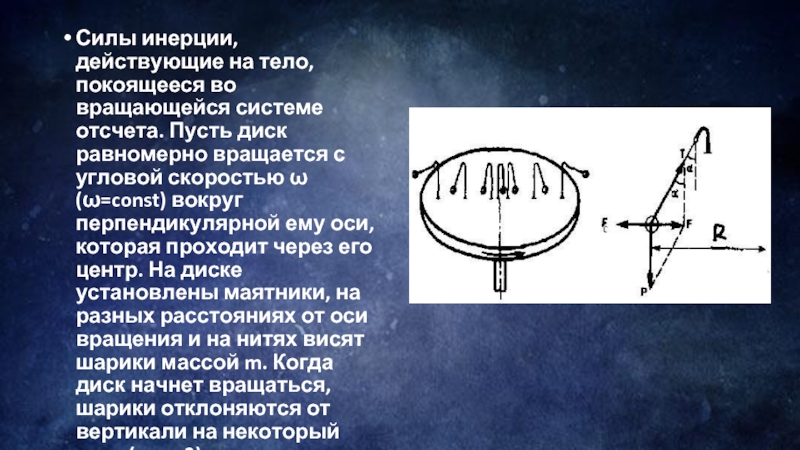
Слайд 6Силы инерции, действующие на тело, покоящееся во вращающейся системе отсчета. Пусть
диск равномерно вращается с угловой скоростью ω (ω=const) вокруг перпендикулярной ему оси, которая проходит через его центр. На диске установлены маятники, на разных расстояниях от оси вращения и на нитях висят шарики массой m. Когда диск начнет вращаться, шарики отклоняются от вертикали на некоторый угол (рис. 2).
Слайд 7В инерциальной системе отсчета, которая связана, например, с помещением, где установлен
диск, происходит равномерное вращение шарика по окружности радиусом R (расстояние от центра вращающегося шарика до оси вращения). Значит, на него действует сила, равная F=mω2R и которая направлена перпендикулярно оси вращения диска. Она является равнодействующей силы тяжести Р и силы реакции (натяжения) нити Т: F=P+T. Когда движение шарика установится, то F=mgtgα=mω2R, откуда
т. е. углы отклонения нитей маятников будут тем больше, чем больше угловая скорость вращения &omega и чем больше расстояние R от центра шарика до оси вращения диска;.
т. е. углы отклонения нитей маятников будут тем больше, чем больше угловая скорость вращения &omega и чем больше расстояние R от центра шарика до оси вращения диска;.
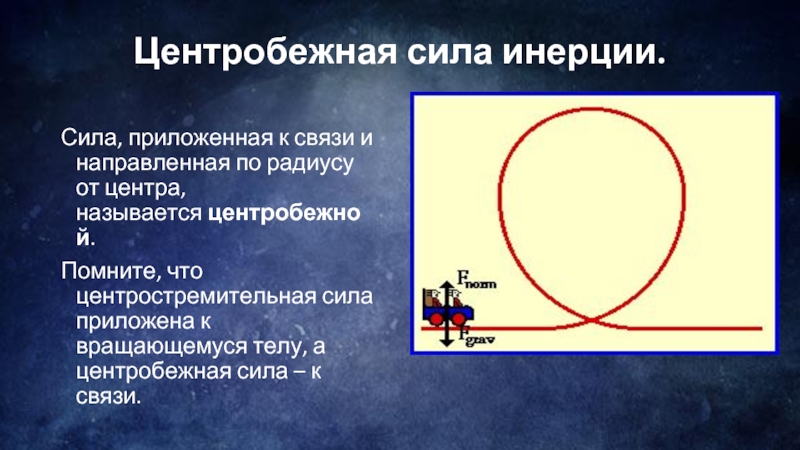
Слайд 11Центробежная сила инерции.
Сила, приложенная к связи и направленная по радиусу от
центра, называется центробежной.
Помните, что центростремительная сила приложена к вращающемуся телу, а центробежная сила – к связи.
Помните, что центростремительная сила приложена к вращающемуся телу, а центробежная сила – к связи.
.
Слайд 12
Центробежная сила – сила инерции первого рода. Центробежной силы, приложенной к вращающемуся
телу, не существует.
С точки зрения наблюдателя, связанного с неинерциальной системой отсчета, он не приближается к центру, хотя видит, что Fцс действует (об этом можно судить по показанию пружинного динамометра). Следовательно, с точки зрения наблюдателя в неинерциальной системе есть сила, уравновешивающая Fцс, равная ей по величине и противоположная по направлению:
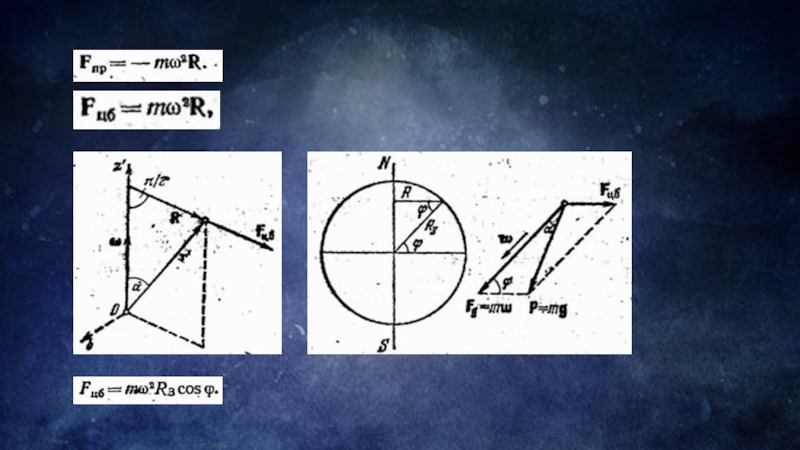
т.к. an = ω2R (здесь ω – угловая скорость вращения камня, а υ – линейная), то
Fцб = m ω2R. (1)
С точки зрения наблюдателя, связанного с неинерциальной системой отсчета, он не приближается к центру, хотя видит, что Fцс действует (об этом можно судить по показанию пружинного динамометра). Следовательно, с точки зрения наблюдателя в неинерциальной системе есть сила, уравновешивающая Fцс, равная ей по величине и противоположная по направлению:
т.к. an = ω2R (здесь ω – угловая скорость вращения камня, а υ – линейная), то
Fцб = m ω2R. (1)
Слайд 13
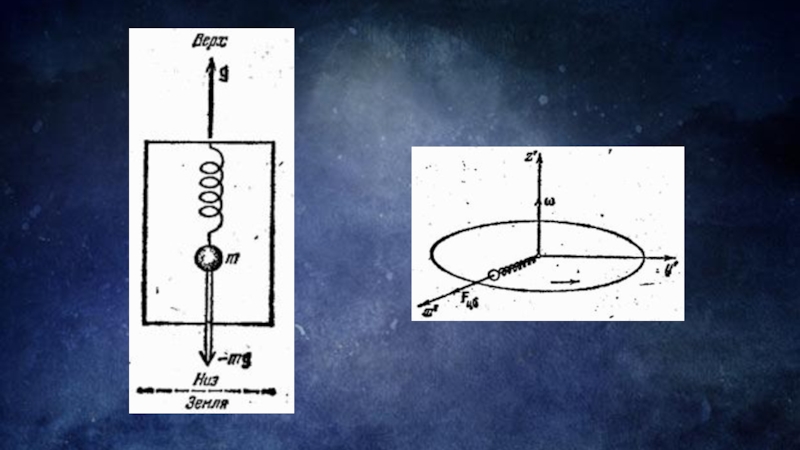
В неинерциальной системе (рис.1) R = RЗ cosφ φ – широта
местности); ω – угловая скорость вращения Земли.
Сила тяжести есть результат сложения двух сил: и , таким образом g (а значит и mg ) зависит от широты местности:
,где g = 9,80665 м/с2 – ускорение свободного падения тела. Направлено g точно к центру только на полюсе и на экваторе.
Сила тяжести есть результат сложения двух сил: и , таким образом g (а значит и mg ) зависит от широты местности:
,где g = 9,80665 м/с2 – ускорение свободного падения тела. Направлено g точно к центру только на полюсе и на экваторе.
Слайд 15Сила Кориолиса.
При движении тела относительно вращающейся системы отсчета, кроме центростремительной и
центробежной сил, появляется еще одна сила, называемая силой Кориолиса или кориолисовой силой инерции (Г. Кориолис (1792 – 1843) – французский физик).
Слайд 16
Появление кориолисовой силы можно обнаружить на следующем примере. Возьмем горизонтально
расположенный диск, который может вращаться вокруг вертикальной оси. Прочертим на диске радиальную прямую ОА (рис.2).
Запустим в направлении от О к А шарик со скоростью . Если диск не вращается, шарик должен катиться вдоль ОА. Если же диск привести во вращение в направлении, указанном стрелкой, то шарик будет катиться по кривой ОВ, причем его скорость относительно диска быстро изменяет свое направление. Следовательно, по отношению к вращающейся системе отсчета шарик ведет себя так, как если бы на него действовала сила , перпендикулярная направлению движения шарика.
Сила Кориолиса не является «настоящей» в смысле механики Ньютона. При рассмотрении движений относительно инерциальной системы отсчета такая сила вообще не существует. Она вводится искусственно при рассмотрении движений в системах отсчета, вращающихся относительно инерциальных, чтобы придать уравнениям движения в таких системах формально такой же вид, что и в инерциальных системах отсчета.
Запустим в направлении от О к А шарик со скоростью . Если диск не вращается, шарик должен катиться вдоль ОА. Если же диск привести во вращение в направлении, указанном стрелкой, то шарик будет катиться по кривой ОВ, причем его скорость относительно диска быстро изменяет свое направление. Следовательно, по отношению к вращающейся системе отсчета шарик ведет себя так, как если бы на него действовала сила , перпендикулярная направлению движения шарика.
Сила Кориолиса не является «настоящей» в смысле механики Ньютона. При рассмотрении движений относительно инерциальной системы отсчета такая сила вообще не существует. Она вводится искусственно при рассмотрении движений в системах отсчета, вращающихся относительно инерциальных, чтобы придать уравнениям движения в таких системах формально такой же вид, что и в инерциальных системах отсчета.
Слайд 17
Чтобы заставить шарик катиться вдоль ОА, нужно сделать направляющую, выполненную в виде
ребра. При качении шарика направляющее ребро действует на него с некоторой силой. Относительно вращающейся системы (диска), шарик движется с постоянной по направлению скоростью. Это можно объяснить тем, что эта сила уравновешивается приложенной к шарику силой инерции:
Здесь – сила Кориолиса, также являющаяся силой инерции, – угловая скорость вращения диска.
Сила Кориолиса вызывает кориолисово ускорение. Выражение для этого ускорения имеет вид: (1)
Здесь – сила Кориолиса, также являющаяся силой инерции, – угловая скорость вращения диска.
Сила Кориолиса вызывает кориолисово ускорение. Выражение для этого ускорения имеет вид: (1)
Слайд 18
Ускорение направлено перпендикулярно векторам и и максимально,
если относительная скорость точки ортогональна угловой скорости вращения подвижной системы отсчета. Кориолисово ускорение равно нулю, если угол между векторами и равен нулю или π, либо если хотя бы один из этих векторов равен нулю.
Следовательно, в общем случае, при использовании уравнений Ньютона во вращающейся системе отсчета, возникает необходимость учитывать центробежную, центростремительную силы инерции, а также кориолисову силу.
Таким образом, всегда лежит в плоскости, перпендикулярной к оси вращения. Сила Кориолиса возникает только в случае, когда тело изменяет свое положение по отношению к вращающейся системе отсчета.
Следовательно, в общем случае, при использовании уравнений Ньютона во вращающейся системе отсчета, возникает необходимость учитывать центробежную, центростремительную силы инерции, а также кориолисову силу.
Таким образом, всегда лежит в плоскости, перпендикулярной к оси вращения. Сила Кориолиса возникает только в случае, когда тело изменяет свое положение по отношению к вращающейся системе отсчета.
Слайд 19
Влияние кориолисовых сил необходимо учитывать в ряде случаев при истолковании
явлений, связанных с движением тел относительно земной поверхности. Например, при свободном падении тел на них действует кориолисова сила, обусловливающая отклонение к востоку от линии отвеса. Эта сила максимальна на экваторе и обращается в нуль на полюсах. Летящий снаряд также испытывает отклонения, обусловленные кориолисовыми силами инерции. Например, при выстреле из орудия, направленного на север, снаряд будет отклоняться к востоку в северном полушарии и к западу – в южном. При стрельбе вдоль экватора силы Кориолиса будут прижимать снаряд к Земле, если выстрел произведен в восточном направлении.
Сила Кориолиса действует на тело, движущееся вдоль меридиана в северном полушарии вправо и в южном – влево (рис. 3).
Это приводит к тому, что у рек подмывается всегда правый берег в северном полушарии и левый – в южном. Эти же причины объясняют неодинаковый износ рельсов железнодорожных путей.
Сила Кориолиса действует на тело, движущееся вдоль меридиана в северном полушарии вправо и в южном – влево (рис. 3).
Это приводит к тому, что у рек подмывается всегда правый берег в северном полушарии и левый – в южном. Эти же причины объясняют неодинаковый износ рельсов железнодорожных путей.
Слайд 20
Силы Кориолиса проявляются и при качаниях маятника (маятник Фуко). Для простоты
предположим, что маятник расположен на полюсе (рис. 4). На северном полюсе сила Кориолиса будет направлена вправо по ходу маятника. В итоге траектория движения маятника будет иметь вид розетки.
Как следует из рисунка, плоскость качаний маятника поворачивается относительно Земли в направлении часовой стрелки, причем за сутки она совершает один оборот. Относительно гелиоцентрической системы отсчета дело обстоит так: плоскость качаний остается неизменной, а Земля поворачивается относительно нее, делая за сутки один оборот.
Таким образом, вращение плоскости качаний маятника Фуко дает непосредственное доказательство вращения Земли вокруг своей оси.
Как следует из рисунка, плоскость качаний маятника поворачивается относительно Земли в направлении часовой стрелки, причем за сутки она совершает один оборот. Относительно гелиоцентрической системы отсчета дело обстоит так: плоскость качаний остается неизменной, а Земля поворачивается относительно нее, делая за сутки один оборот.
Таким образом, вращение плоскости качаний маятника Фуко дает непосредственное доказательство вращения Земли вокруг своей оси.
Слайд 21
Если тело удаляется от оси вращения, то сила
направлена противоположно вращению и замедляет его.
Если тело приближается к оси вращения, то направлена в сторону вращения.
С учетом всех сил инерции, уравнение Ньютона для неинерциальной системы отсчета (1) примет вид:
– сила инерции, обусловленная поступательным движением неинерциальной системы отсчета; – две силы инерции, обусловленные вращательным движением системы отсчета; – ускорение тела относительно неинерциальной системы отсчета:
С учетом всех сил инерции, уравнение Ньютона для неинерциальной системы отсчета (1) примет вид:
– сила инерции, обусловленная поступательным движением неинерциальной системы отсчета; – две силы инерции, обусловленные вращательным движением системы отсчета; – ускорение тела относительно неинерциальной системы отсчета:
Слайд 23
Ма́ятник Фуко́ — маятник, используемый для экспериментальной демонстрации суточного вращения Земли.
Первая публичная демонстрация была
осуществлена в марте 1851 года в парижском Пантеоне: под куполом Пантеона он подвесил металлический шар массой 28 кг с закреплённым на нём остриём на стальной проволоке длиной 67 м. Крепление маятника позволяло ему свободно колебаться во всех направлениях, под точкой крепления было сделано круговое ограждение диаметром 6 м, по краю ограждения была насыпана песчаная дорожка таким образом, чтобы маятник в своём движении мог при её пересечении прочерчивать на песке отметки. Чтобы избежать бокового толчка при пуске маятника, его отвели в сторону и привязали верёвкой, после чего верёвку пережгли.
Период колебания маятника при такой длине подвеса составлял 16,4 секунды, при каждом колебании отклонение от предыдущего пересечения песчаной дорожки составляло около 3 мм, за час плоскость колебаний маятника поворачивалась более чем на 11° по часовой стрелке, то есть примерно за 32 часа совершала полный оборот и возвращалась в прежнее положение.
Период колебания маятника при такой длине подвеса составлял 16,4 секунды, при каждом колебании отклонение от предыдущего пересечения песчаной дорожки составляло около 3 мм, за час плоскость колебаний маятника поворачивалась более чем на 11° по часовой стрелке, то есть примерно за 32 часа совершала полный оборот и возвращалась в прежнее положение.
Слайд 24
Маятник Фуко является математическим маятником, плоскость колебаний которого медленно поворачивается относительно земной
поверхности в сторону, противоположную направлению вращения Земли.
На Северном или Южном полюсе Земли (ось вращения Земли лежит в плоскости колебаний маятника) плоскость колебаний маятника Фуко совершает поворот на 360° за звёздные сутки (на 15° за звёздный час), на экваторе (ось вращения Земли перпендикулярна плоскости колебаний маятника) плоскость колебаний маятника Фуко неподвижна, в произвольной точке с географической широтой ɸ (угол между осью вращения Земли и плоскостью колебаний маятника α=90⁰ - ɸ )скорость вращения плоскости колебаний идеального маятника Фуко ꭥᵨ (в градусах в звёздный час) относительно поверхности Земли составляет
ꭥᵨ=15sinɸ
Поскольку период колебаний зависит от длины подвеса( ) , то увеличение длины нити увеличивает угол поворота, совершаемого плоскостью вращения за один период, что и используют при демонстрации.
На Северном или Южном полюсе Земли (ось вращения Земли лежит в плоскости колебаний маятника) плоскость колебаний маятника Фуко совершает поворот на 360° за звёздные сутки (на 15° за звёздный час), на экваторе (ось вращения Земли перпендикулярна плоскости колебаний маятника) плоскость колебаний маятника Фуко неподвижна, в произвольной точке с географической широтой ɸ (угол между осью вращения Земли и плоскостью колебаний маятника α=90⁰ - ɸ )скорость вращения плоскости колебаний идеального маятника Фуко ꭥᵨ (в градусах в звёздный час) относительно поверхности Земли составляет
ꭥᵨ=15sinɸ
Поскольку период колебаний зависит от длины подвеса( ) , то увеличение длины нити увеличивает угол поворота, совершаемого плоскостью вращения за один период, что и используют при демонстрации.