- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Схематизация опор. Определение реакций презентация
Содержание
- 1. Схематизация опор. Определение реакций
- 2. Опорные реакции и реакции в жесткой заделке
- 3. q l₁ l₂ l₃
- 4. q l₁ l₂ l₃
- 5. q l₁ l₂ l₃
- 6. q l₁ l₂ l₃
- 7. q l₁ l₂ l₃
- 8. q l₁ l₂ l₃
- 9. l₁ l₂ Дано: F= 2
- 10. l₁ l₂ Дано: F= 2
- 11. q=2 l₁ l₂ l₃
- 12. q=2 l₁ l₂ l₃
- 13. Если Q =
- 14. При построении эпюр следует руководствоваться приведенными правилами:
- 15. Правильность построения эпюр Q и М
- 16. q=2 l₁ =1 l₂ =3 l₃=2
- 17. Определение реакций Пример 1. Определить реакции.
- 18. Определение опорных реакций Пример 2. Определить
- 19. Определение реакций Пример 3. Определить реакции
- 20. Определение опорных реакций Пример 4. Определить реакции.
- 21. Определение реакций Пример 5. Определить реакции. При
- 22. Определение реакций Пример 6. Определить реакции.
- 23. l₁
- 24. Определяем реакции связей (опорные реакции). Используя принцип
- 25. l₁ l₂
- 26. Проверим правильность определения реакций, составив уравнение
- 27. l₁ l₂
- 28. l₁ l₂
- 29. l₁ А q
- 30. l₁ А q
- 31. l₁ А q
- 32. l₁ А q
- 35. l₂ В
- 37. При проверке эпюр следует ось
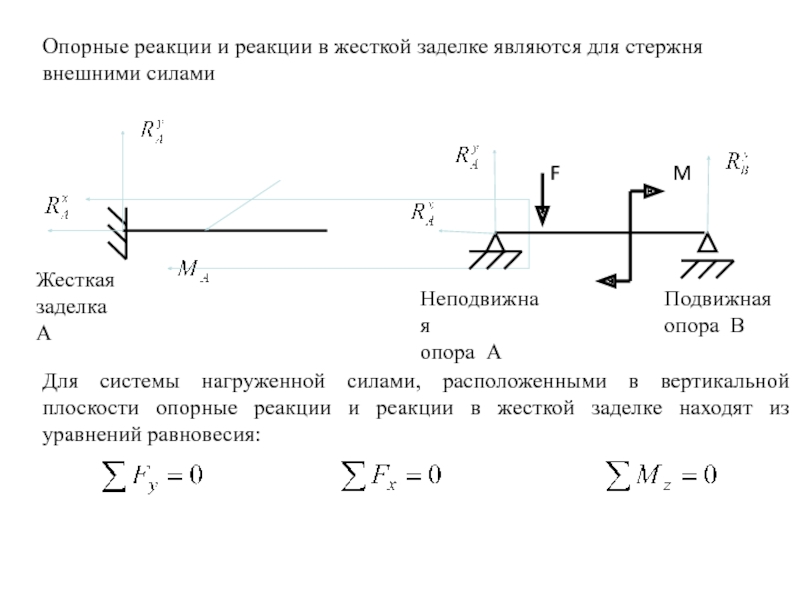
Слайд 2Опорные реакции и реакции в жесткой заделке являются для стержня внешними
Неподвижная
опора А
Подвижная
опора В
Жесткая заделка А
Для системы нагруженной силами, расположенными в вертикальной плоскости опорные реакции и реакции в жесткой заделке находят из уравнений равновесия:
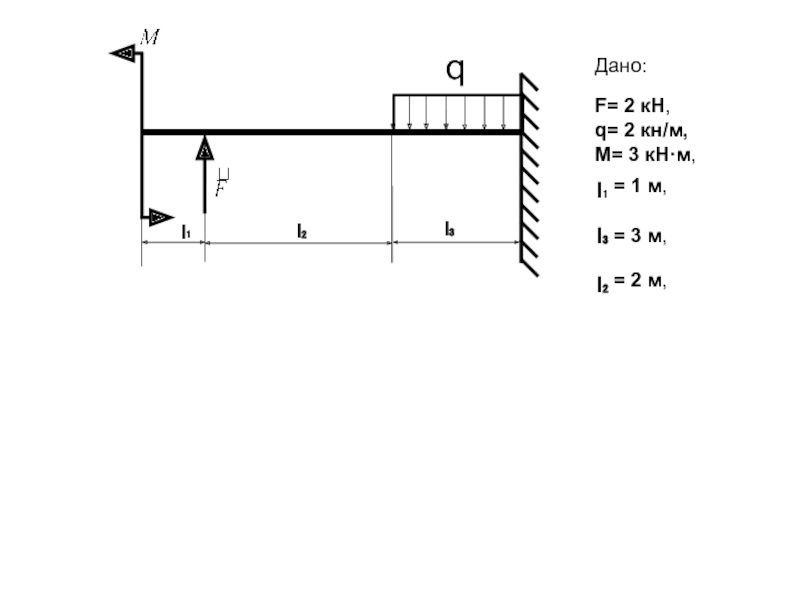
Слайд 4
q
l₁
l₂
l₃
Дано:
F= 2 кН,
q= 2 кн/м,
М= 3 кН·м,
l₁
l₂
l₃
= 1 м,
= 2 м,
= 3 м,
1 участок
2 участок
3 участок
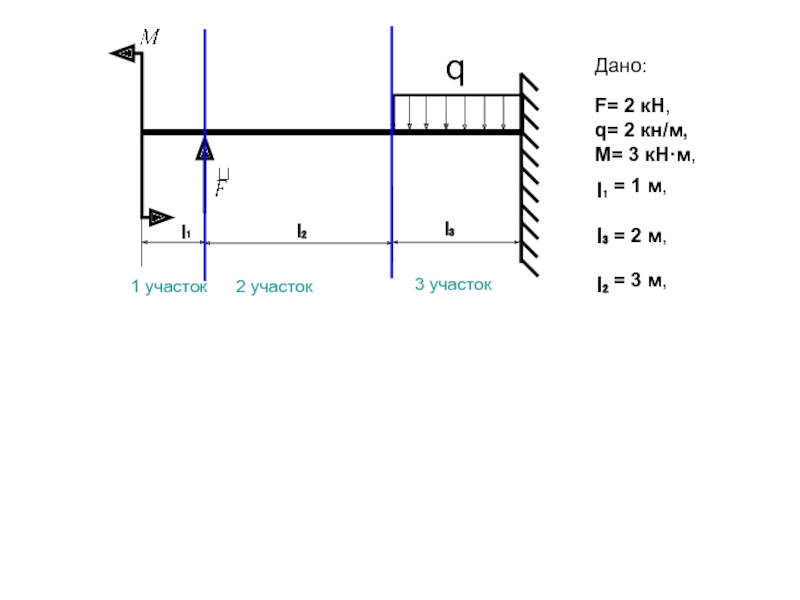
Слайд 5
q
l₁
l₂
l₃
Дано:
F= 2 кН,
q= 2 кн/м,
М= 3 кН·м,
l₁
l₂
l₃
= 1 м,
= 3 м,
= 2 м,
1 участок
2 участок
3 участок
1
1
2
2
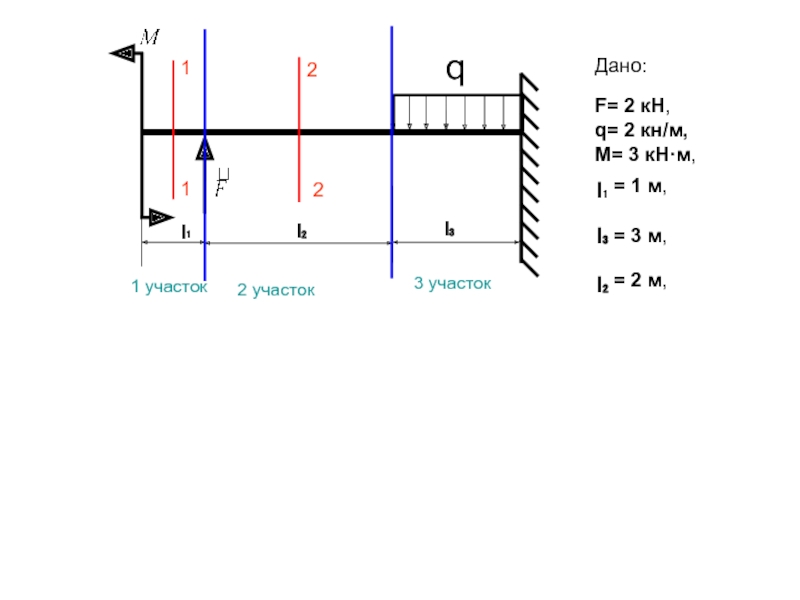
Слайд 6
q
l₁
l₂
l₃
Дано:
F= 2 кН,
q= 2 кн/м,
М= 3 кН·м,
l₁
l₂
l₃
= 1 м,
= 3 м,
= 2 м,
1 участок
2 участок
3 участок
1
1
2
2
3
3
Слайд 7
q
l₁
l₂
l₃
Дано:
F= 2 кН,
q= 2 кн/м,
М= 3 кН·м,
l₁
l₂
l₃
= 1 м,
= 3 м,
= 2 м,
1 участок
2 участок
1 участок
2
2
3
3
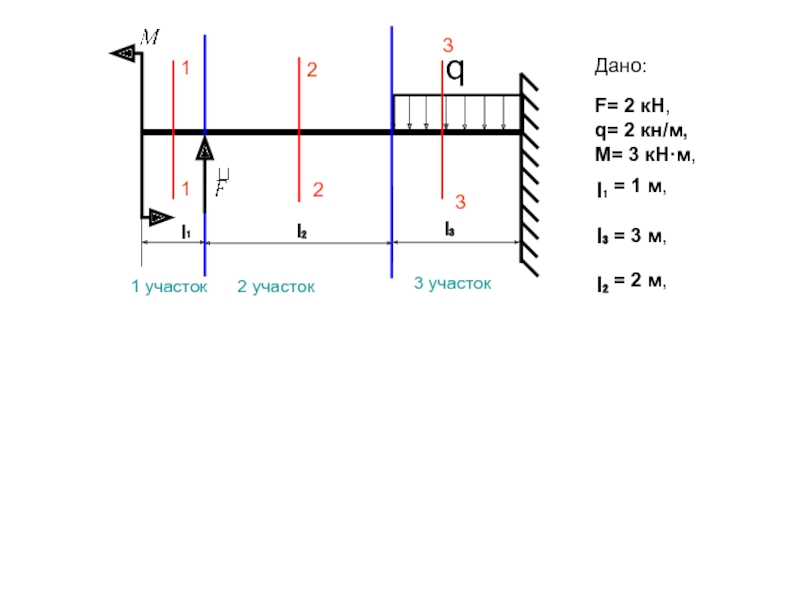
0 Х 1 м
х
= 0,
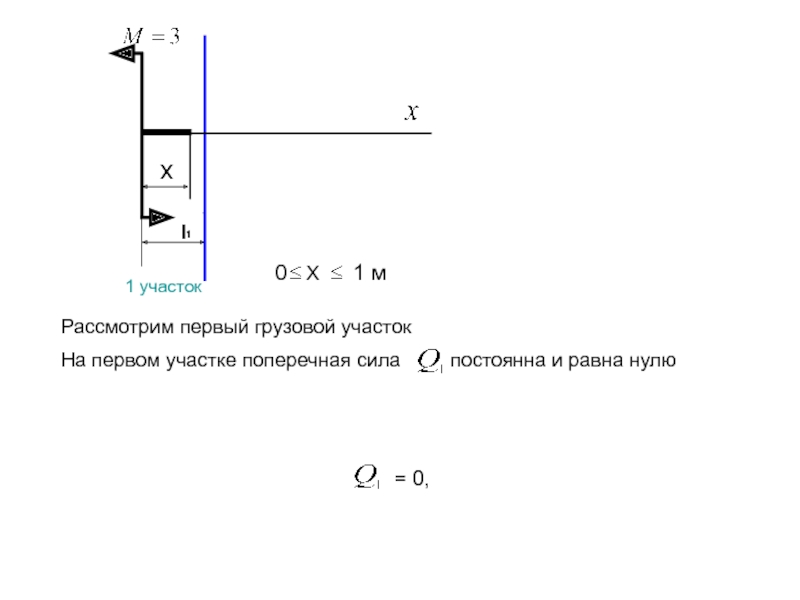
Рассмотрим первый грузовой участок
На первом участке поперечная сила постоянна и равна нулю
Слайд 8
q
l₁
l₂
l₃
Дано:
F= 2 кН,
q= 2 кн/м,
М= 3 кН·м,
l₁
l₂
l₃
= 1 м,
= 3 м,
= 2 м,
1 участок
2 участок
1 участок
2
2
3
3
0 Х 1 м
х
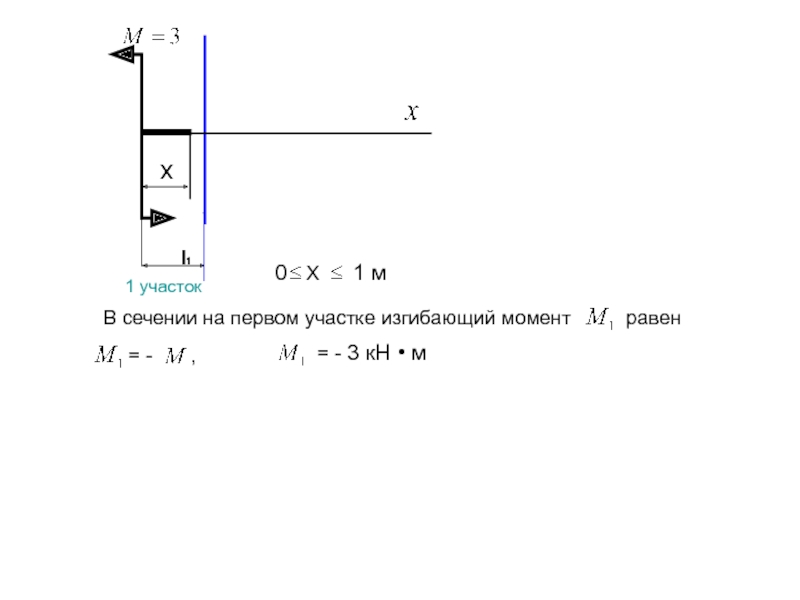
В сечении на первом участке изгибающий момент равен
= - ,
= - 3 кН • м
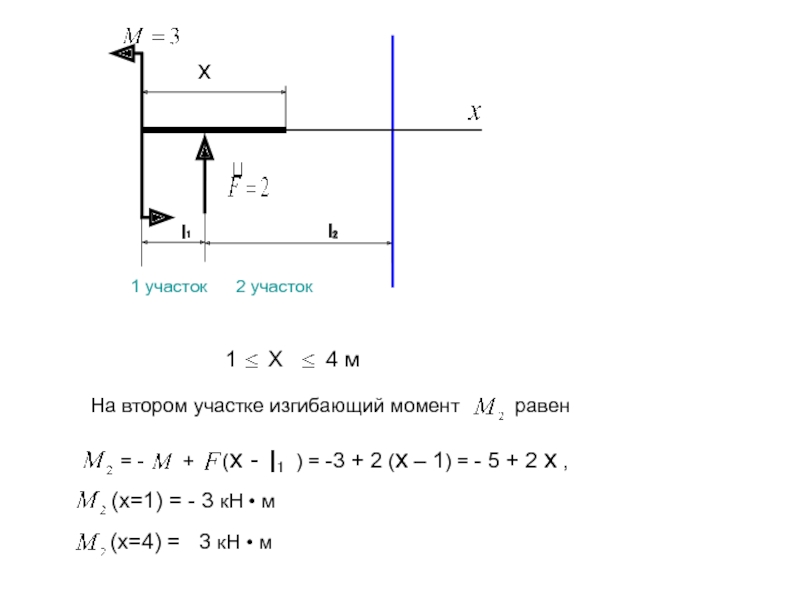
Слайд 9l₁
l₂
Дано:
F= 2 кН,
q= 2 кн/м,
М= 3 кН·м,
l₁
l₂
l₃
= 1 м,
= 3 м,
= 2 м,
1 участок
2 участок
х
1 Х 4 м
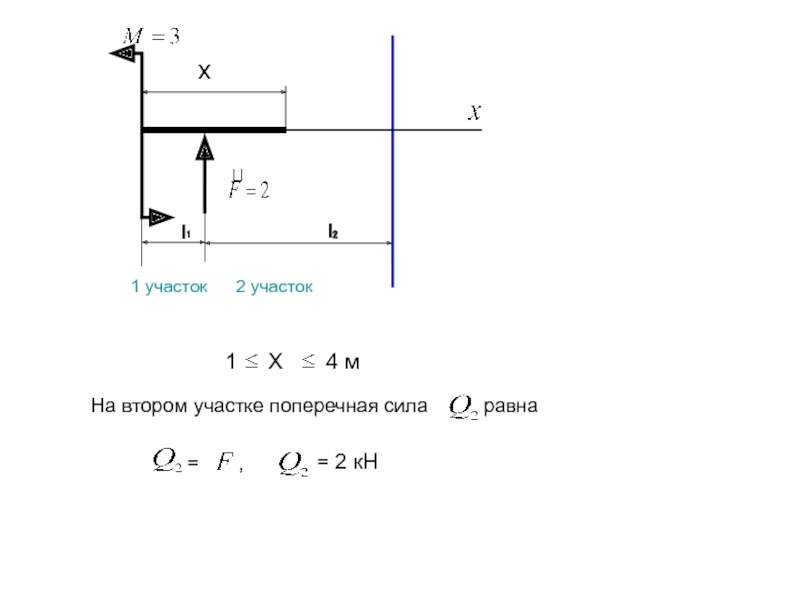
На втором участке поперечная сила равна
= ,
= 2 кН
Слайд 10l₁
l₂
Дано:
F= 2 кН,
q= 2 кн/м,
М= 3 кН·м,
l₁
l₂
l₃
= 1 м,
= 3 м,
= 2 м,
1 участок
2 участок
х
1 Х 4 м
На втором участке изгибающий момент равен
= - + (х - ) = -3 + 2 (х – 1) = - 5 + 2 х ,
l₁
(x=1) = - 3 кН • м
(x=4) = 3 кН • м
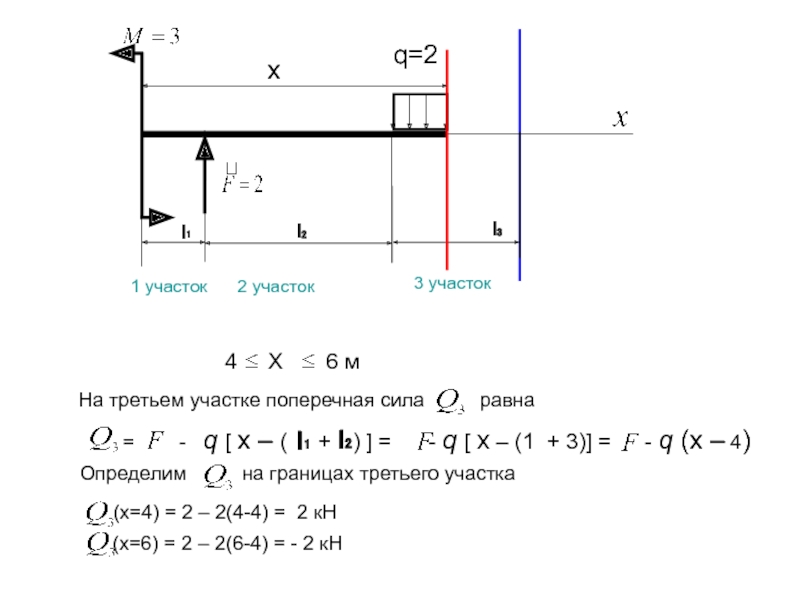
Слайд 11
q=2
l₁
l₂
l₃
1 участок
2 участок
3 участок
х
4 Х
На третьем участке поперечная сила равна
= - q [ х – ( + l₂) ] = - q [ х – (1 + 3)] = - q (х – 4)
l₁
(x=4) = 2 – 2(4-4) = 2 кН
(x=6) = 2 – 2(6-4) = - 2 кН
Определим на границах третьего участка
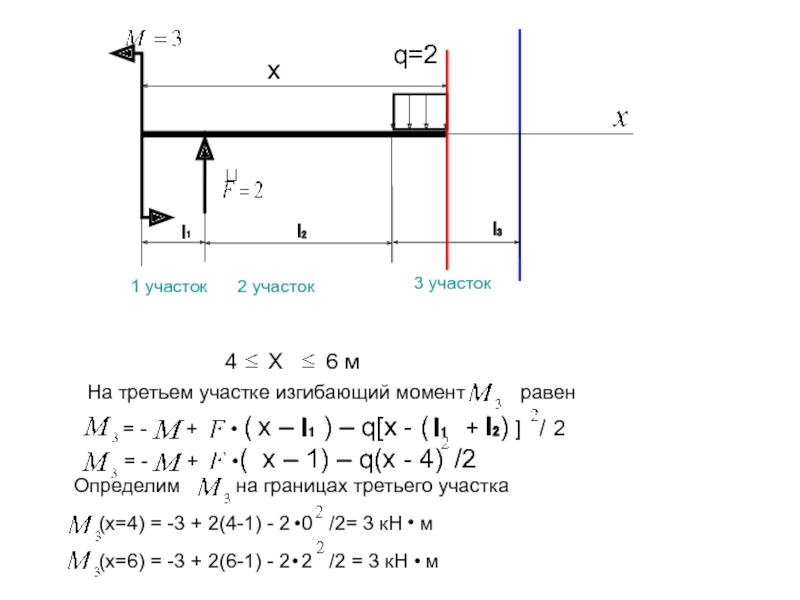
Слайд 12
q=2
l₁
l₂
l₃
1 участок
2 участок
3 участок
х
4 Х
На третьем участке изгибающий момент равен
= - + • ( х – ) – q[х - ( + l₂) ] / 2
l₁
(x=4) = -3 + 2(4-1) - 2 0 /2= 3 кН м
(x=6) = -3 + 2(6-1) - 2 2 /2 = 3 кН м
l₁
= - + •( х – 1) – q(х - 4) /2
Определим на границах третьего участка
•
•
•
•
Слайд 13
Если Q = = 0, то
= - q (х – 4) = 0
2-2 (х – 4)=0 , х = 5 м
Максимум момента равен 4 кН• м
Слайд 14При построении эпюр следует руководствоваться приведенными правилами:
Эпюру моментов строят на сжатом
Пользуясь принципом смягченных граничных условий, будем полагать, что в сечении, где приложена сосредоточенная сила, значение поперечной силы меняется скачкообразно, причем скачок равен модулю этой силы.
На том же основании будем полагать, что в сечении, где приложена пара сил (момент), значение изгибающего момента меняется скачкообразно, причем скачок равен моменту пары.
Если в каком-либо сечении балки приложена сосредоточенная сила, то на эпюре поперечных сил в этом сечении будет скачок на величину силы, а на эпюре изгибающих моментов произойдет излом эпюры.
Если участок балки загружен равномерно распределенной нагруз-кой q, то на эпюра поперечных сил на этом участке ограничена наклонной прямой, а эпюра моментов – кривой второго порядка.
Слайд 15 Правильность построения эпюр Q и М следует проверять с помощью
Между изгибающим моментом, поперечной силой и интенсивностью
распределенной нагрузки существуют дифференциальные зависимости, основанные на теореме Журавского.
Эта теорема формулируется так: поперечная сила равна первой производной от изгибающего момента по абсциссе сечения балки.
q= = Q = = tg ,
где — угол, который составляет касательная к эпюре моментов с положительным направлением оси x.
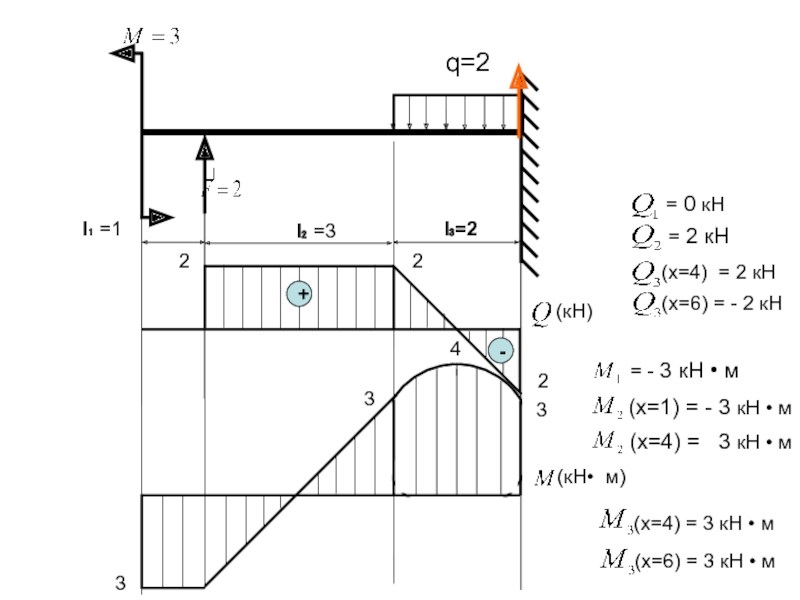
Слайд 16
q=2
l₁ =1
l₂ =3
l₃=2
+
-
2
2
2
3
3
3
(кН)
(кН• м)
= 0 кН
= - 3 кН
= 2 кН
(x=1) = - 3 кН • м
(x=4) = 3 кН • м
(x=4) = 2 кН
(x=6) = - 2 кН
(x=4) = 3 кН • м
(x=6) = 3 кН • м
4
Слайд 17Определение реакций
Пример 1. Определить реакции.
2м
3м
F= 5 кН
А
В
RA
RB
H
3. Из уравнений статики
RB · 5 – F · 2 = 0. RB = (5 · 2) / 5 = 2 кН.
х
y
RА · 5 – F · 3 = 0. RА = (5 · 3) / 5 = 3 кН.
-HA = 0. HA = 0.
R А + RB – F = 0.
3 + 2 – 5 = 0. 0 = 0.
А
1. Показываем реакции.
2. Считаем число реакций
= 2 кН
= 3 кН
∑ МА = 0.
∑ Мв = 0.
∑ Х = 0.
Проверка: ∑ Y= 0.
= 0
Подписываем реакции.
Слайд 18
Определение опорных реакций
Пример 2. Определить реакции.
5 кН
3 кН
1. Показываем реакции.
А
RA
RB
HB
3. Определяем реакции.
a
х
х
y
5 кН
7 кН
H
б
Σ MA = 0.
l = 2 м
a
б
Σ X = 0.
= 2 кН
x
x
y
B
A
2. Считаем число реакций/
Σ X = 0.
Σ Y = 0.
RB·2 = 0. RB = 0.
RA + RB = 0. RA= 0.
HB +3 - 5 = 0. HB = 2 кН
Н – 7 + 5 = 0. Н = 2 кН
= 0
= 0
= 2кН
0
0
Заделка считается в этой точке
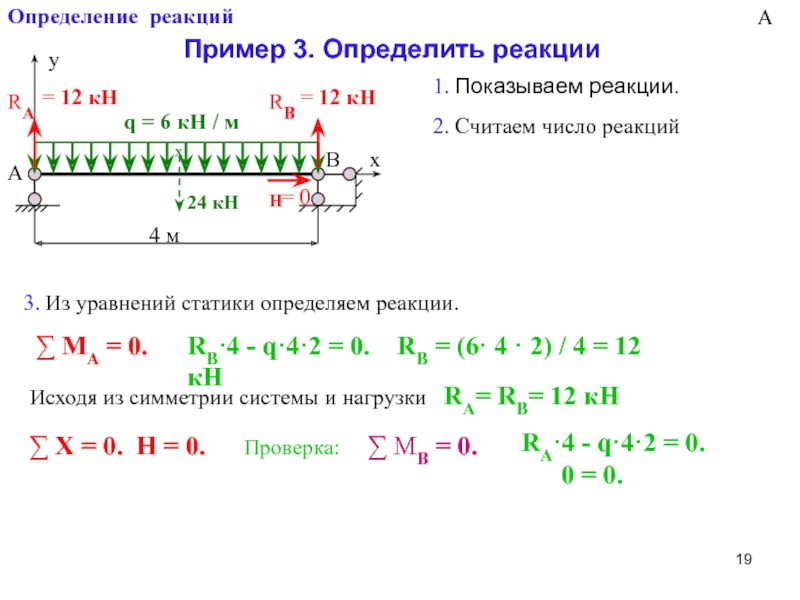
Слайд 19Определение реакций
Пример 3. Определить реакции
х
y
q = 6 кН / м
А
В
RA
4 м
RВ
х
24
кН
Н
RB·4 - q·4·2 = 0. RB = (6· 4 · 2) / 4 = 12 кН
Исходя из симметрии системы и нагрузки RA= RB= 12 кН
∑ Х = 0. Н = 0.
RА·4 - q·4·2 = 0.
0 = 0.
А
3. Из уравнений статики определяем реакции.
∑ МА = 0.
Проверка: ∑ МВ = 0.
= 12 кН
= 12 кН
2. Считаем число реакций
1. Показываем реакции.
= 0
Слайд 20Определение опорных реакций
Пример 4. Определить реакции.
А
В
М = 5 кН·м
3 м
2 м
F
RA
RB
H
1. Показываем реакции.
2. Считаем число реакций
3. Определяем реакции.
∑ Х = 0. -Н = 0. Н = 0.
х
y
∑ МА = 0.
∑ МВ = 0.
Проверка: ∑ Y = 0.
А
= -1 кН
= 5 кН
= 0
RB = (4 · 5 – 5) / 3 = 5 кН
RB ·3 - F·5 + М = 0.
RА = (- 4 · 2 + 5) / 3 = - 1 кН < 0
-RА ·3 - F·2 + М = 0.
RA + RB – F = 0. -1 + 5 – 4 = 0. 0 = 0.
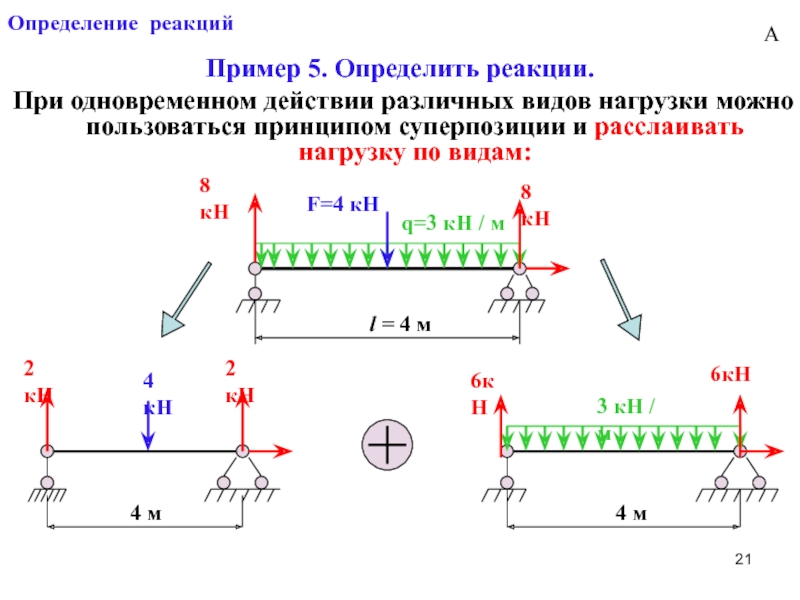
Слайд 21Определение реакций
Пример 5. Определить реакции.
При одновременном действии различных видов нагрузки можно
F=4 кН
q=3 кН / м
l = 4 м
4 м
4 кН
3 кН / м
4 м
8 кН
2 кН
6кН
6кН
2 кН
8 кН
А
Слайд 22Определение реакций
Пример 6. Определить реакции.
F = ql
q
M = ql 2
2 l
RA
RB
= - 0.33 ql
= 1.33 ql
Н
= 0
∑ МА = 0.
– q ∙2l ∙ l + M +F ∙2l + RB∙3l = 0;
– q ∙2l ∙ l + ql 2 + ql ∙2l + RB ∙3l = 0;
RB = - 0.33 ql < 0
∑MB = 0.
RA = 1.33 ql.
– RA∙3l + q∙2l ∙2l + ql 2 – ql ∙l = 0;
– RA∙3l + q∙2l ∙2l + M - F ∙l = 0;
Проверка : ∑ Y = 0.
RA + RB – q∙2l + F = 0;
0 = 0.
1.33 ql – 0.33 ql – 2ql + ql = 0.
Показываем реакции.
2. Считаем число реакций .
3. Определяем реакции.
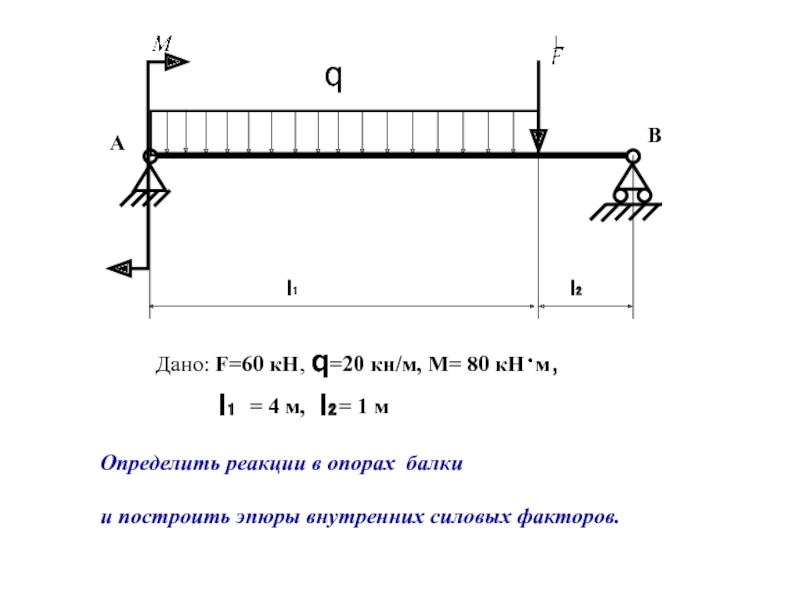
Слайд 23
l₁
l₂
А
В
q
Дано: F=60 кН, q=20 кн/м, М= 80 кН·м,
l₁
=
l₂
Определить реакции в опорах балки
и построить эпюры внутренних силовых факторов.
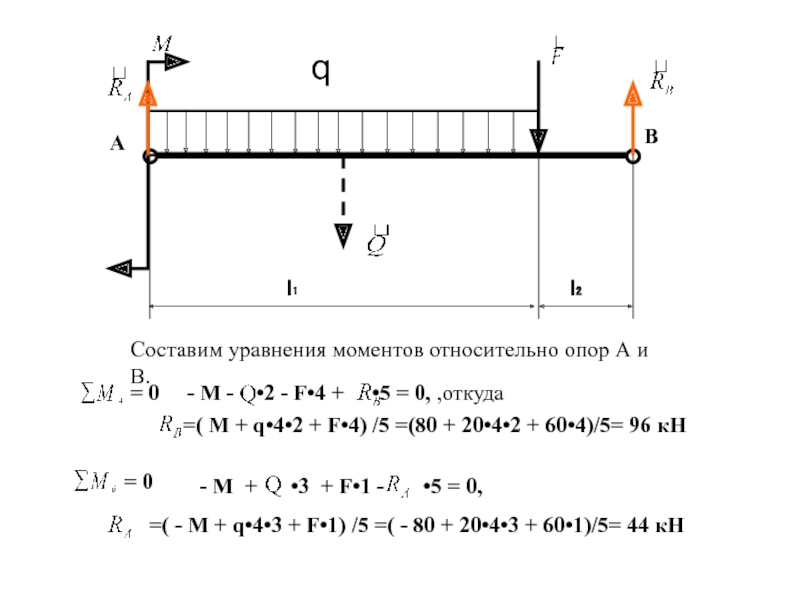
Слайд 24Определяем реакции связей (опорные реакции).
Используя принцип освобождаемости от связей представляем тело
Слайд 25
l₁
l₂
А
В
q
Составим уравнения моментов относительно опор А и В.
= 0
-
=( М + q•4•2 + F•4) /5 =(80 + 20•4•2 + 60•4)/5= 96 кН
= 0
- М + •3 + F•1 - •5 = 0,
=( - М + q•4•3 + F•1) /5 =( - 80 + 20•4•3 + 60•1)/5= 44 кН
Слайд 26Проверим правильность определения реакций, составив уравнение
проекций
=0
+ - 4•q - F = 44 + 96 – 80 – 60 = 0
Полученное тождество 0 = 0 говорит о том, что реакции определены правильно.
Разобьем балку на грузовые участки и применим метод сечений.
Напомним, что в общем случае границами участков балки являются концы
балки, опоры, начало и конец распределенной нагрузки, точки приложения
сосредоточенных сил и внешних моментов.
Слайд 28
l₁
l₂
А
В
q
первый грузовой участок
второй грузовой участок
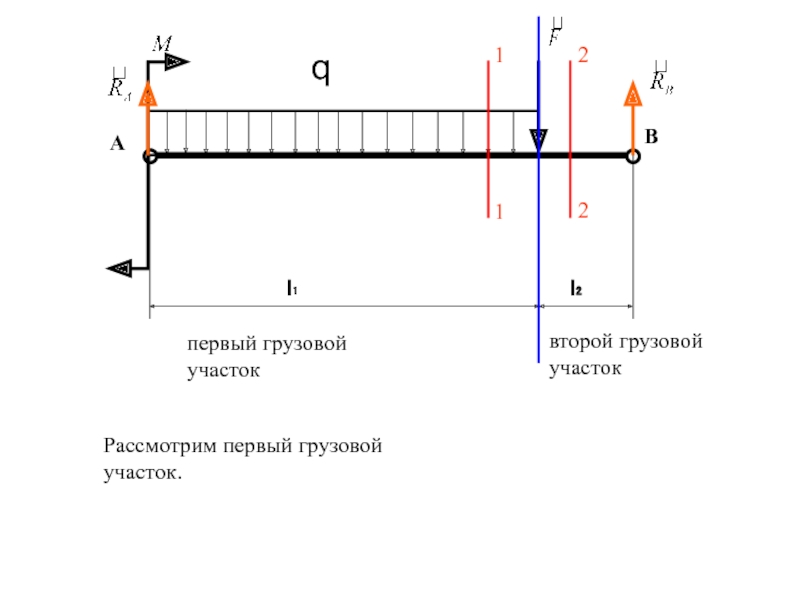
Рассмотрим первый грузовой участок.
1
1
2
2
Слайд 29
l₁
А
q
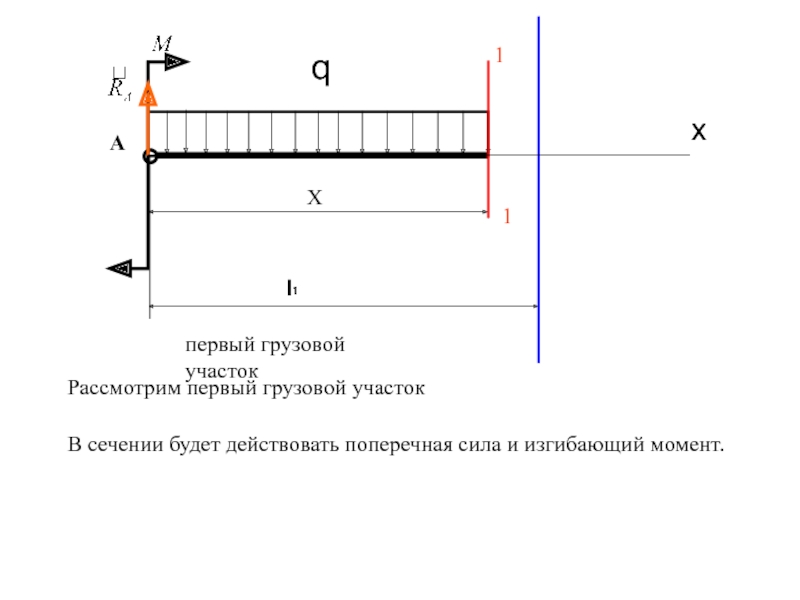
первый грузовой участок
В сечении будет действовать поперечная сила и изгибающий
1
1
Х
x
Рассмотрим первый грузовой участок
Слайд 30
l₁
А
q
первый грузовой участок
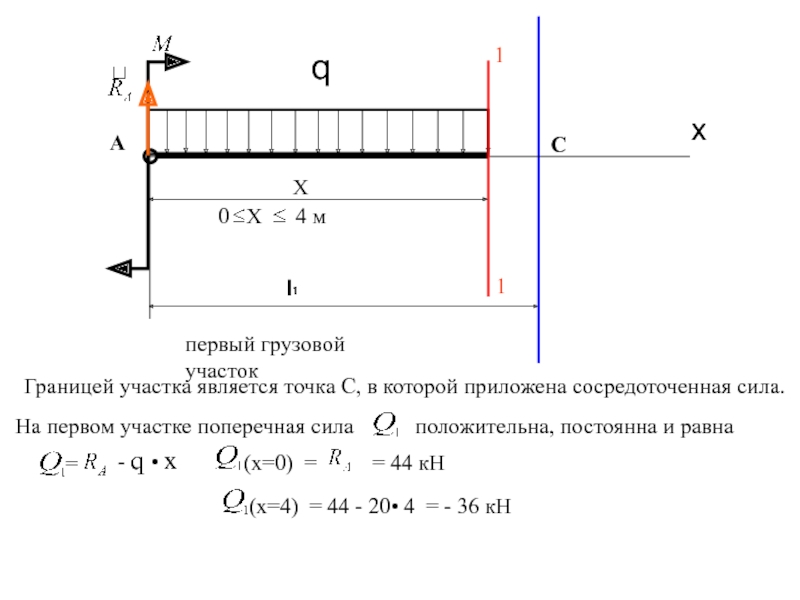
С
x
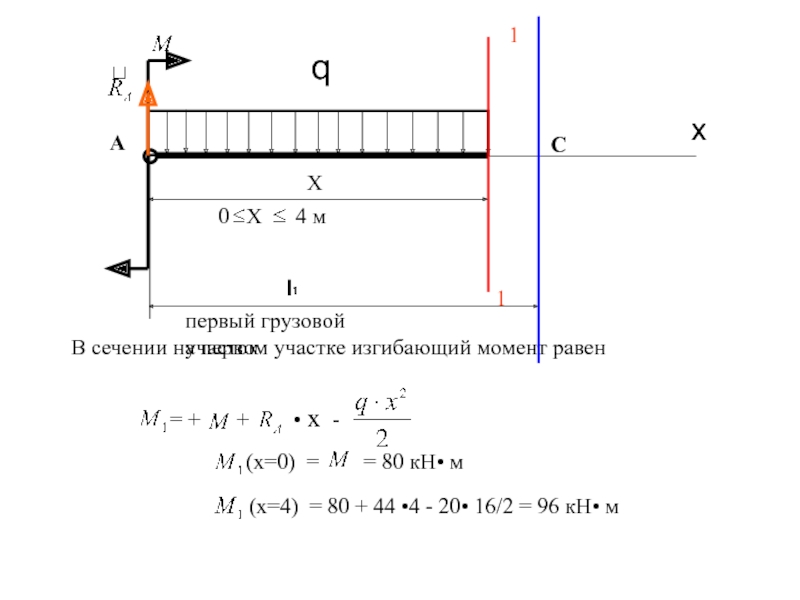
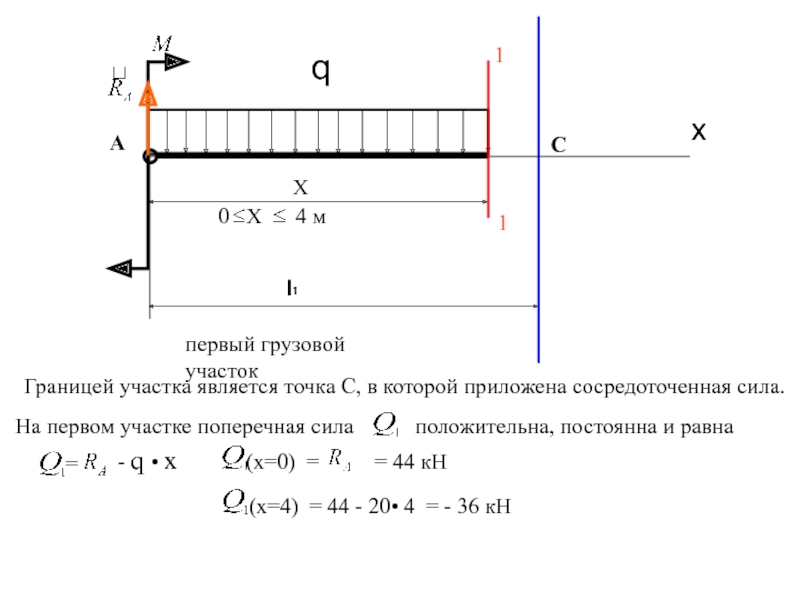
Границей участка является точка С, в которой приложена
На первом участке поперечная сила положительна, постоянна и равна
=
- q • x
(x=0) = = 44 кН
(x=4) = 44 - 20• 4 = - 36 кН
0 Х 4 м
1
1
Х
Слайд 31
l₁
А
q
первый грузовой участок
С
x
+ • x -
(x=0) = = 80 кН• м
(x=4) = 80 + 44 •4 - 20• 16/2 = 96 кН• м
0 Х 4 м
В сечении на первом участке изгибающий момент равен
= +
1
1
Х
Слайд 32
l₁
А
q
первый грузовой участок
С
x
Границей участка является точка С, в которой приложена
На первом участке поперечная сила положительна, постоянна и равна
=
- q • x
(x=0) = = 44 кН
(x=4) = 44 - 20• 4 = - 36 кН
0 Х 4 м
1
1
Х
Слайд 33
А
В
q
2,2 м
+
-
-
+
44
36
96
80
(кН)
(кН• м)
128,4
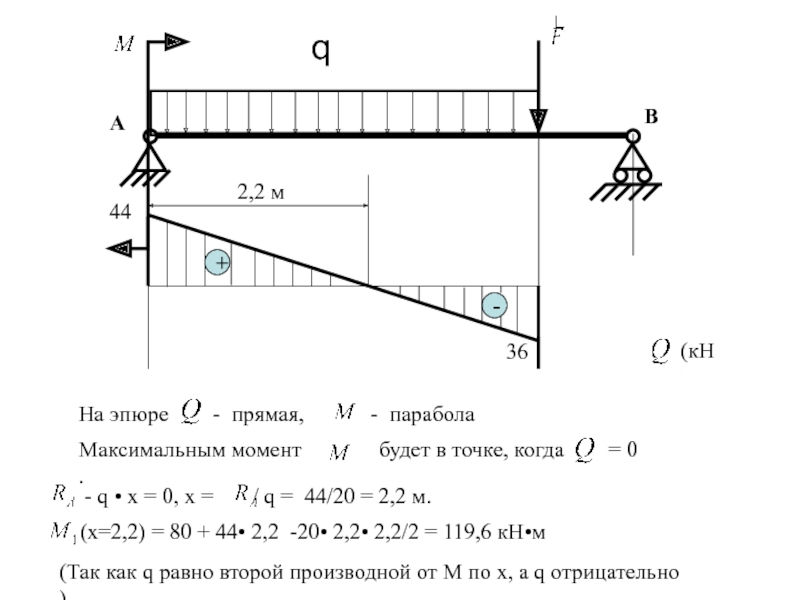
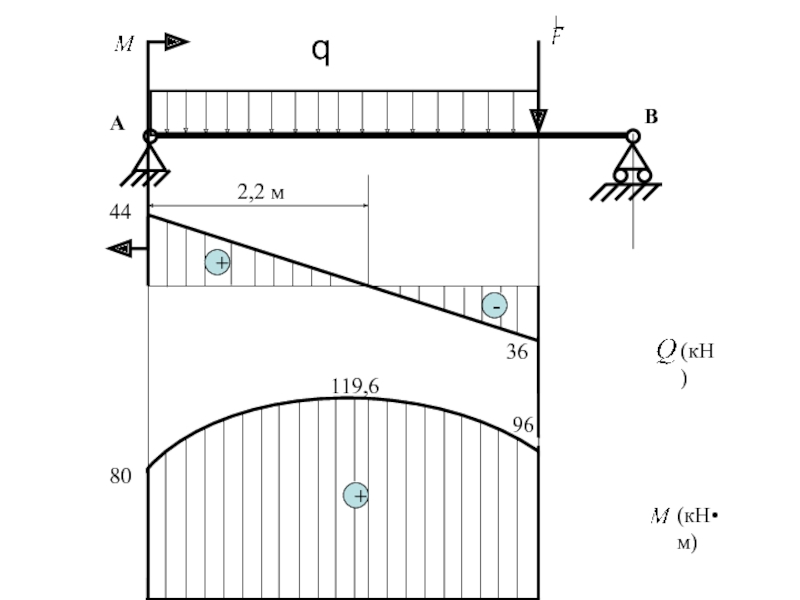
На эпюре - прямая,
Максимальным момент будет в точке, когда = 0 .
- q • x = 0, х = / q = 44/20 = 2,2 м.
(x=2,2) = 80 + 44• 2,2 -20• 2,2• 2,2/2 = 119,6 кН•м
(Так как q равно второй производной от М по х, а q отрицательно )
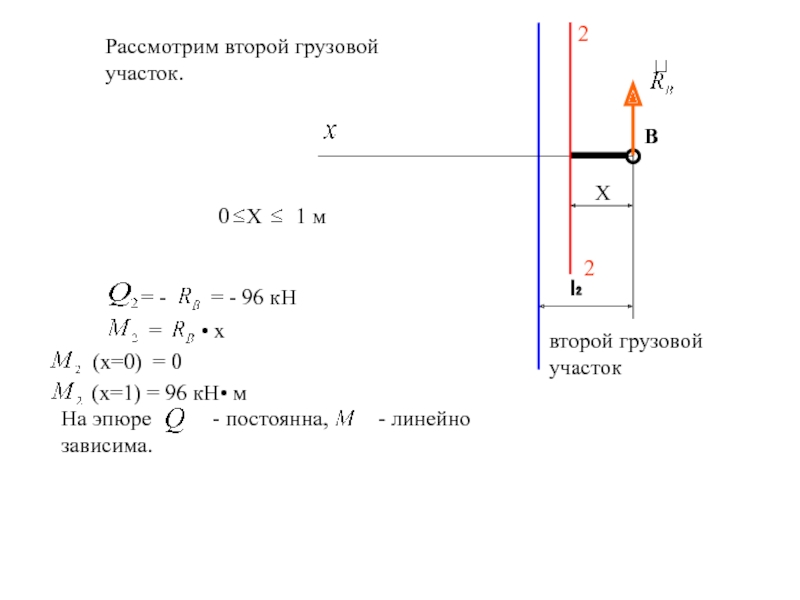
Слайд 35
l₂
В
второй грузовой участок
Рассмотрим второй грузовой участок.
0 Х
= - = - 96 кН
(x=1) = 96 кН• м
(x=0) = 0
На эпюре - постоянна, - линейно зависима.
= • х
2
2
Х
Слайд 37При проверке эпюр следует ось мысленно всегда
На участке, где нет распределенной нагрузки, эпюра моментов,представляет собой наклонную прямую, а эпюра поперечных сил — прямую, параллельную оси.
На участке, где приложена равномерно распределенная нагрузка, эпюра моментов представляет собой параболу, а эпюра поперечных сип — наклонную прямую.
На конце балки изгибающий момент равен нулю, если там не приложена пара сил.
При построении эпюры для консольных балок начало координат удобно брать на конце консоли, что нередко дает возможность обойтись без определения опорных реакций.
В сечении, соответствующем заделке, поперечная сила равна реактивной силе, а изгибающий момент — реактивному моменту.