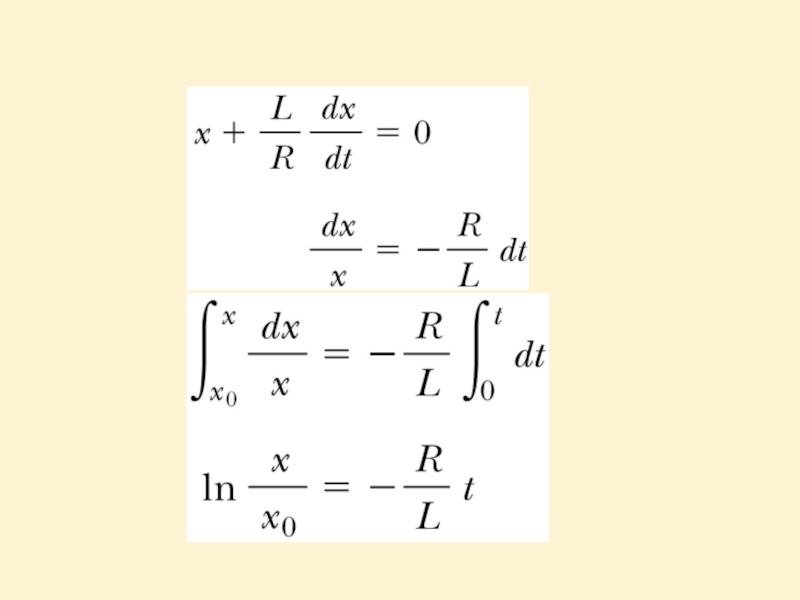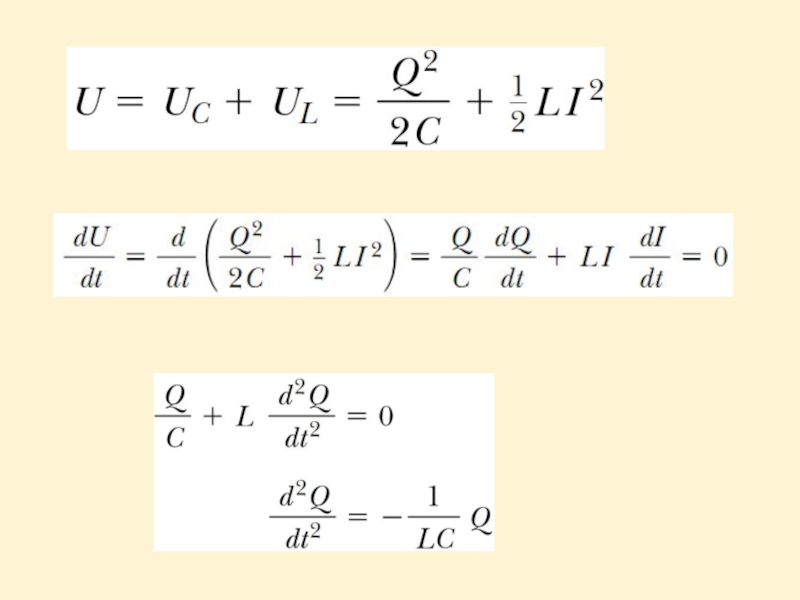- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Self-inductance презентация
Содержание
- 1. Self-inductance
- 2. Lecture 14 Inductunce Self-inductunce RL Circuits Energy
- 3. When the switch is thrown to its
- 4. (a) A current in the coil produces
- 5. Self-induced emf From Faraday’s law follows that
- 6. From last expression it follows that
- 7. Ideal Solenoid Inductance Combining the last expression
- 8. An inductor in a circuit opposes changes
- 10. Taking the antilogarithm of the last result:
- 11. The time constant τ is the time
- 12. Multiplying by I the expression for RL–circuit
- 13. After integration of the last formula:
- 14. Inductance for solenoid is: The magnetic
- 15. uB is the energy density of the
- 16. A cross-sectional view of two adjacent coils.
- 17. Mutual inductance depends on the geometry of
- 18. The emf induced by coil 1 in
- 19. Although the proportionality constants M12 and M21
- 20. If the capacitor is initially charged and
- 22. The solution for the equation
- 23. Then the current is: Choosing
- 24. Graph of charge versus time
- 25. Plots of UC versus t and UL
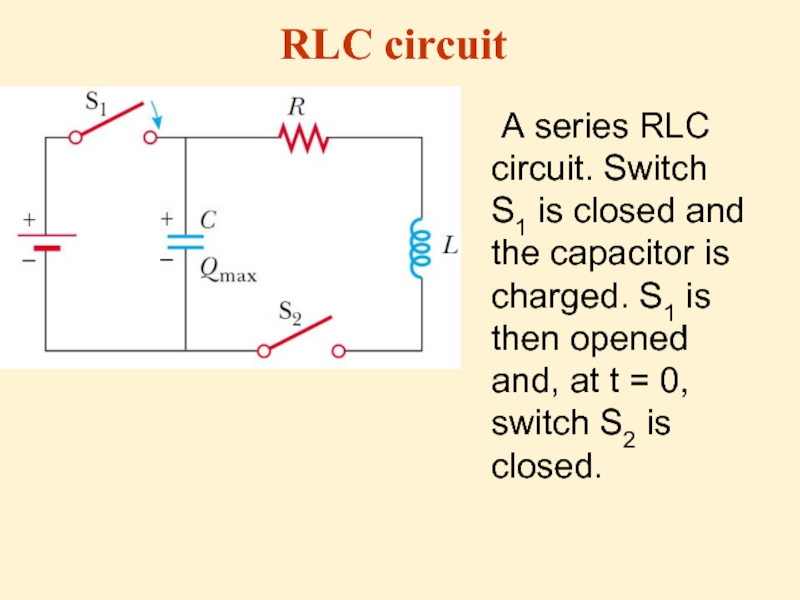
- 26. A series RLC circuit. Switch S1 is
- 27. Energy is dissipated on the resistor:
- 28. The RLC circuit is analogous to the
- 31. Units in Si Inductance L H
Слайд 1Republic of Kazakhstan
Ministry of Education and Science
Kazakh-British Technical University
Faculty of
Physical Engineering Department
Physics 1
Voronkov Vladimir Vasilyevich
Слайд 2Lecture 14
Inductunce
Self-inductunce
RL Circuits
Energy in a Magnetic Field
Mutual inductance
LC circuit – harmonic
RLC circuit – damped harmonic oscillations
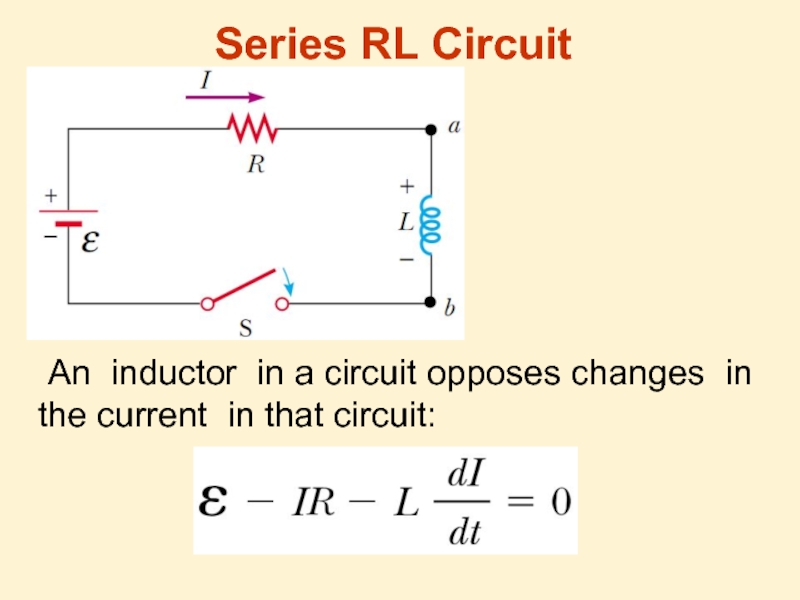
Слайд 3 When the switch is thrown to its closed position, the current
Self-inductance
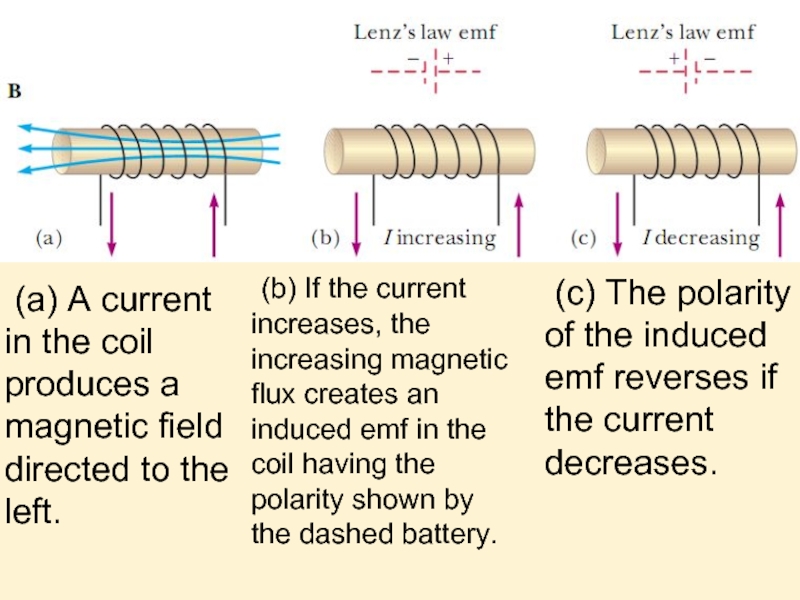
Слайд 4 (a) A current in the coil produces a magnetic field directed
(b) If the current increases, the increasing magnetic flux creates an induced emf in the coil having the polarity shown by the dashed battery.
(c) The polarity of the induced emf reverses if the current decreases.
Слайд 5Self-induced emf
From Faraday’s law follows that the induced emf is equal
L is a proportionality constant—called the inductance of the coil—that depends on the geometry of the coil and other physical characteristics.
Слайд 6From last expression it follows that
So inductance is a measure of
Слайд 7Ideal Solenoid Inductance
Combining the last expression with Faraday’s law, εL =
Слайд 10Taking the antilogarithm of the last result:
Because I = 0 at
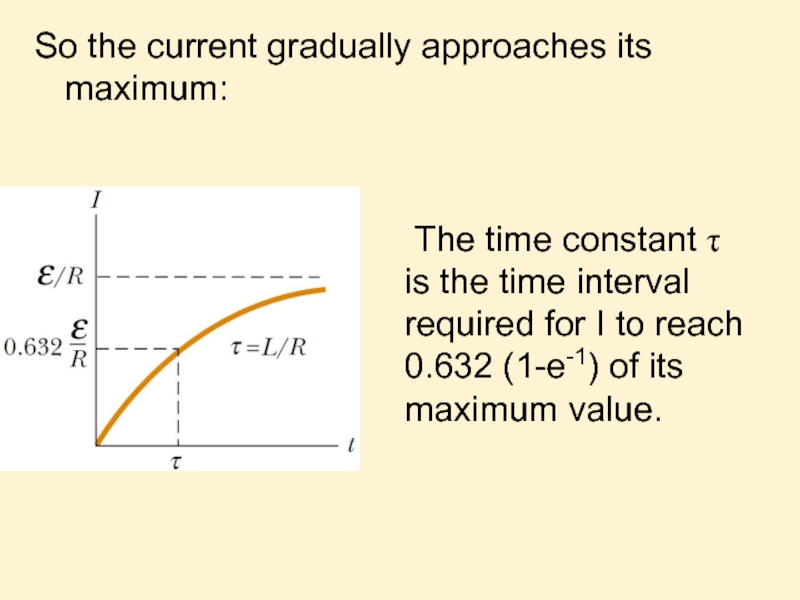
Слайд 11 The time constant τ is the time interval required for I
So the current gradually approaches its maximum:
Слайд 12 Multiplying by I the expression for RL–circuit we obtain:
So here Iε
Energy in an Inductor
Слайд 13After integration of the last formula:
L is the inductance of the
I is the current in the inductor,
U is the energy stored in the magnetic field of the inductor.
Слайд 14Inductance for solenoid is:
The magnetic field of a solenoid is:
Then:
Al is
Magnetic Field Energy Density
Слайд 15uB is the energy density of the magnetic field
B is the
μ0 is the free space permeability for the magnetic field, a constant.
Though this formula was obtained for solenoid, it’s valid for any region of space where a magnetic field exists.
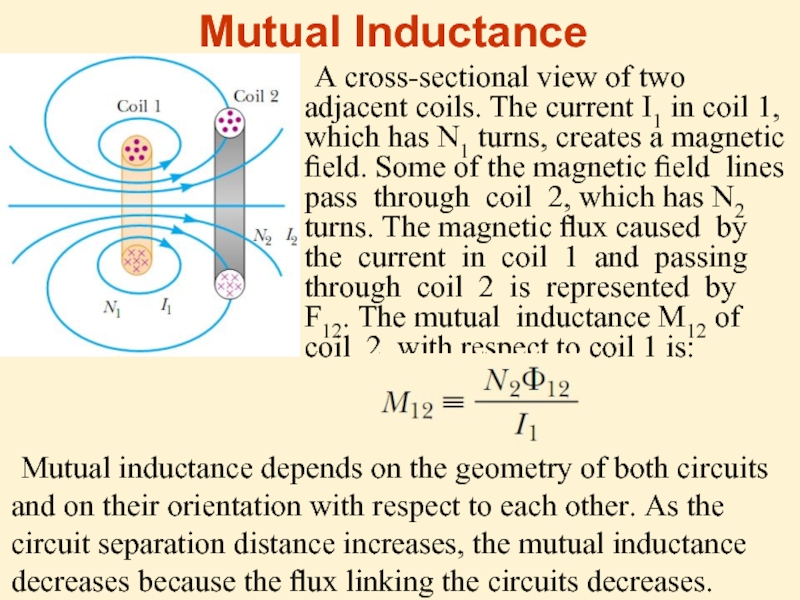
Слайд 16 A cross-sectional view of two adjacent coils. The current I1 in
Mutual Inductance
Mutual inductance depends on the geometry of both circuits and on their orientation with respect to each other. As the circuit separation distance increases, the mutual inductance decreases because the flux linking the circuits decreases.
Слайд 17Mutual inductance depends on the geometry of both circuits and on
Слайд 18The emf induced by coil 1 in coil 2 is:
The preceding
In mutual induction, the emf induced in one coil is always proportional to the rate at which the current in the other coil is changing.
Слайд 19 Although the proportionality constants M12 and M21 have been obtained separately,
These two expression are similar to that for the self-induced emf: ε = - L(dI/dt).
The unit of mutual inductance is the henry.
Слайд 20If the capacitor is initially charged and the switch is then
We assume:
the resistance of the circuit is zero, then no energy is dissipated,
energy is not radiated away from the circuit.
LC Circuit Oscillations
Слайд 22
The solution for the equation is:
The angular frequency of the
Слайд 23Then the current is:
Choosing the initial conditions: at t = 0,
Eventually, the charge in the capacitor and the current in the inductor are:
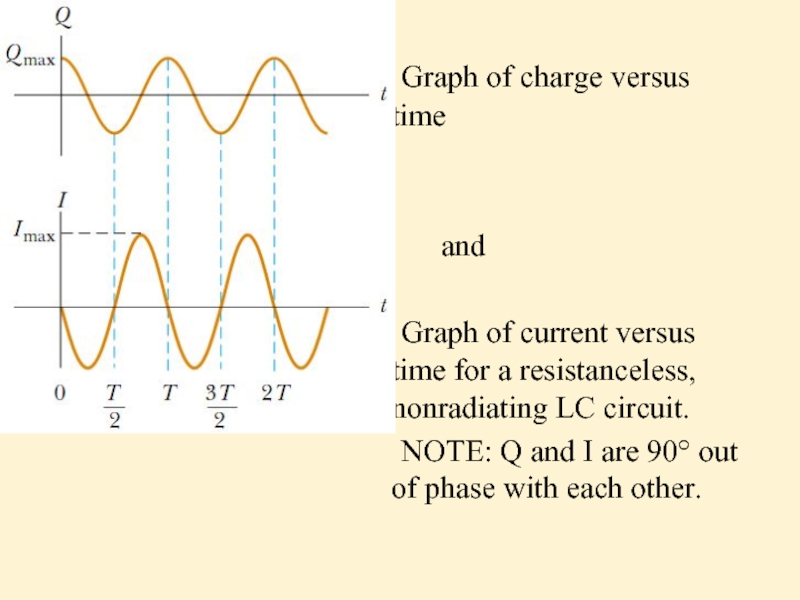
Слайд 24
Graph of charge versus time
and
Graph of current versus time for
NOTE: Q and I are 90° out of phase with each other.
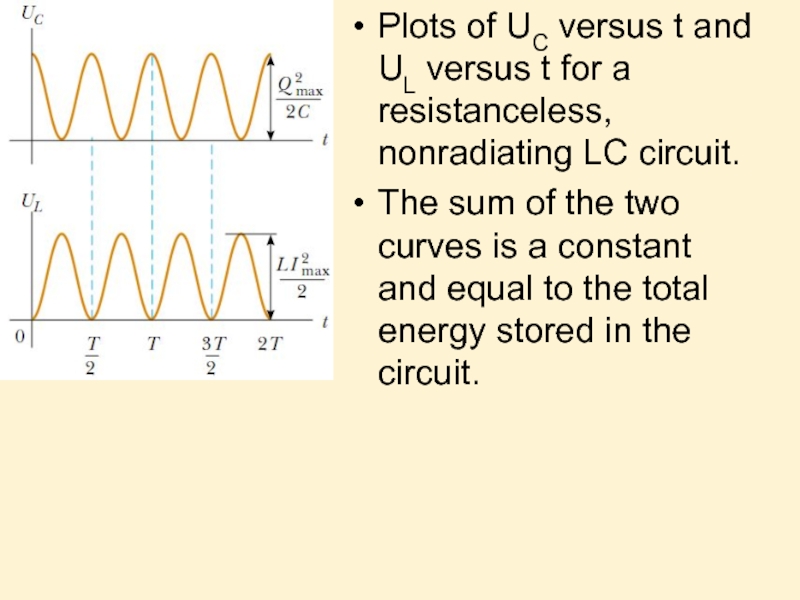
Слайд 25Plots of UC versus t and UL versus t for a
The sum of the two curves is a constant and equal to the total energy stored in the circuit.
Слайд 26 A series RLC circuit. Switch S1 is closed and the capacitor
RLC circuit
Слайд 27Energy is dissipated on the resistor:
Using the equation for dU/dt in
Using that I=dQ/dt:
Слайд 28The RLC circuit is analogous to the damped harmonic oscillator, where
Here b is damping coefficient. When b=0, we have pure harmonic oscillations.
Solution is:
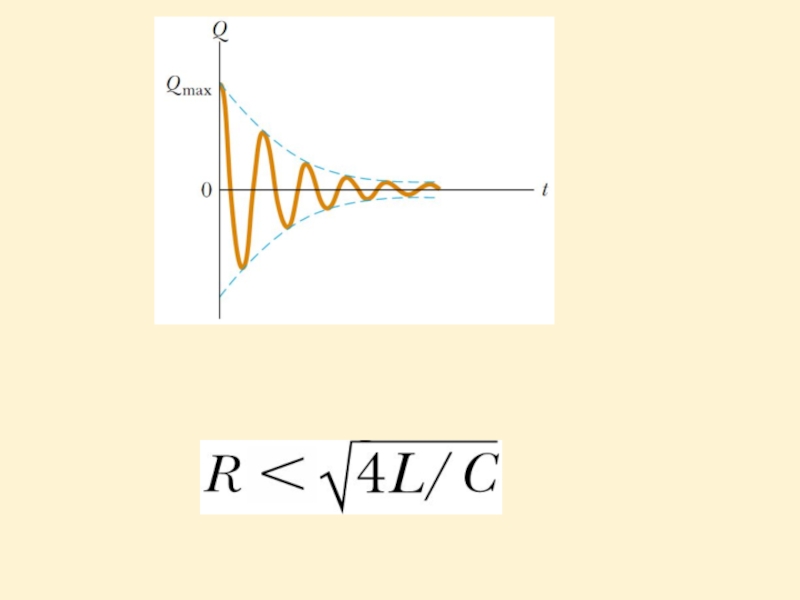
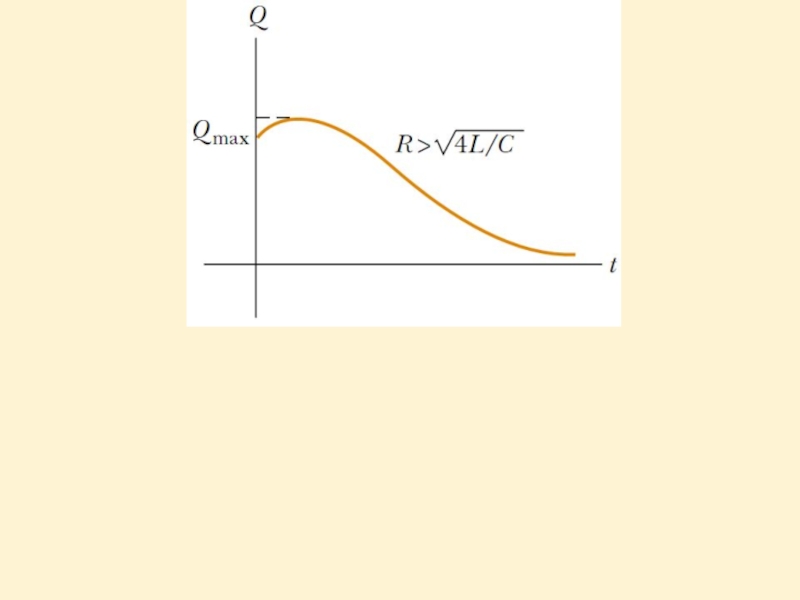
RC is the critical resistance:
When R