- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Реологический метод определения формы частиц презентация
Содержание
- 1. Реологический метод определения формы частиц
- 2. Реология - наука о деформации и течении
- 3. Реологические методы решения технологических задач нашли свое
- 4. Структурно-реологические свойства. Наряду с развитой межфазной
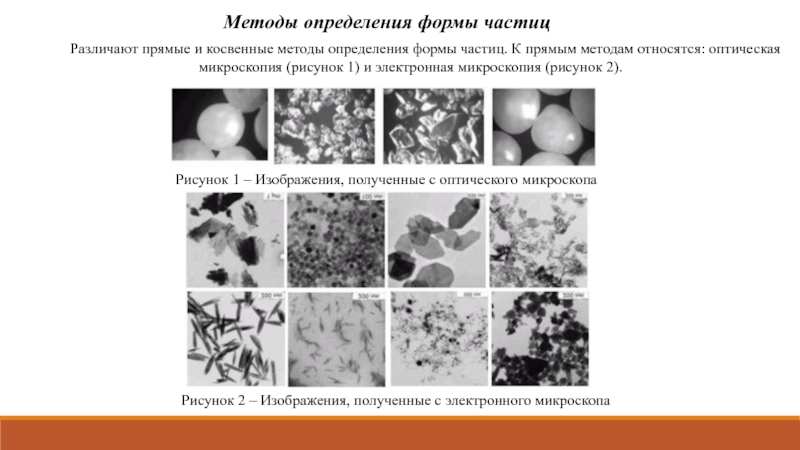
- 6. Методы определения формы частиц Различают прямые и
- 7. К косвенным методам относятся: методы светорассеяния
- 11. Реологический метод определения формы частиц основывается на
- 12. Таблица 1 – Основные параметры формы частиц
- 13. В настоящее время активно развивается математическое моделирование
- 14. Математическое моделирование при анализе процесса деформации элементарной
- 15. Для построения кривых предельного состояния порошковых материалов
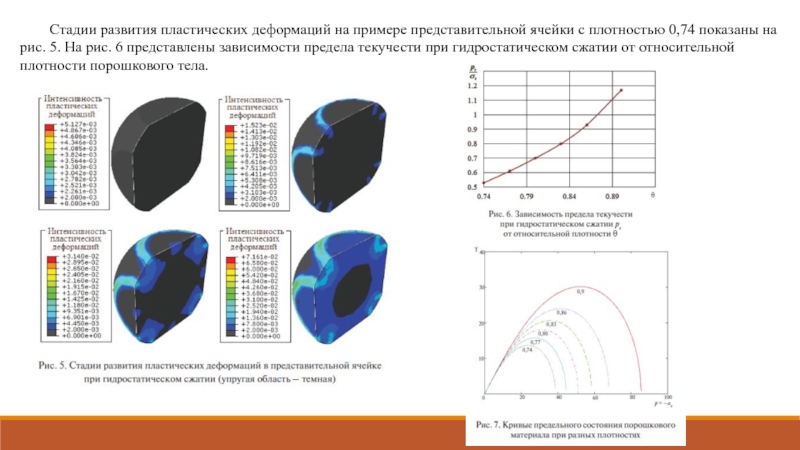
- 16. Стадии развития пластических деформаций на примере
Слайд 2 Реология - наука о деформации и течении различных тел, она изучает
Реология включает два раздела: первый посвящен изучению реологических или в более общем смысле структурно-механических свойств реальных тел, второй рассматривает движение реальных тел в рабочих органах машин и аппаратов и разрабатывает инженерные способы их расчета.
Для проведения реологических исследований свойства тел выражают в виде математических (идеализированных) моделей или уравнений, которые с той или иной степенью точности характеризуют поведение реального тела в процессе деформирования.
Слайд 3 Реологические методы решения технологических задач нашли свое применение в металлургии, в
Реология как самостоятельная наука выделилась из механики деформируемых сред лишь в начале ХХ в. В середине ХХ в. реологические методы решения технологических задач уже применялись в металлургии, производстве полимеров, в промышленных технологиях по производству стекла и строительных материалов, а также других промышленных технологиях. Так, реология как раздел механики деформируемых металлических сред используется уже более полувека для установления зависимостей в процессах их нагружения. Прежде всего, между напряжениями и деформациями. В этом случае реологические уравнения записываются в виде функционалов тензоров напряжений
и тензоров деформаций
, характеризующих диаграмму нагружения
Вид истинной диаграммы нагружения зависит от физических свойств деформируемого материала, а также от технологических свойств в процессах их нагружения
Слайд 4 Структурно-реологические свойства.
Наряду с развитой межфазной поверхностью, обусловливающей многие свойства порошков
Форма частиц.
Форма частиц порошка может быть разной в зависимости от способа его получения. Форма частиц влияет на насыпную плотность порошка, его текучесть, прессуемость и прочность прессовок.
Слайд 6Методы определения формы частиц
Различают прямые и косвенные методы определения формы частиц.
Рисунок 1 – Изображения, полученные с оптического микроскопа
Рисунок 2 – Изображения, полученные с электронного микроскопа
Слайд 7 К косвенным методам относятся: методы светорассеяния и реологические измерения.
Метод
Для определения реологического метода введём понятие дисперсных систем:
Если одно вещество, находящееся в раздробленном (диспергированном) состоянии, равномерно распределено в массе другого вещества, то такую систему называют дисперсной.
В таких системах раздробленное вещество принято называть дисперсной фазой, а среду, в которой она распределена, - дисперсионной средой.
Слайд 11Реологический метод определения формы частиц основывается на том, что разбавленные агрегативно-устойчивые
где η0 – вязкость дисперсионной среды; φф– объемная доля дисперсной фазы; α – коэффициент формы частиц.
По зависимостям η= f(φф) определяют значение коэффициента α и делают вывод о форме частиц (рис.3)
Рисунок 3 – К определению формы частиц по уравнению вязкости Эйнштейна
Соотношения длины частицы (L) к её диаметру (d)
Слайд 13 В настоящее время активно развивается математическое моделирование процессов уплотнения порошковых материалов.
Для исследования выберем порошок алюминия АКВ-2.5
Для разработки расчетно-экспериментальной методики определения реологических характеристик порошкового материала рассмотрим идеализированную модель порошкового тела, состоящего из сферических частиц одинакового размера. При приложении нагрузки уплотнение такого тела в замкнутом объеме осуществляется за счет пластической деформации материала частиц.
Пример
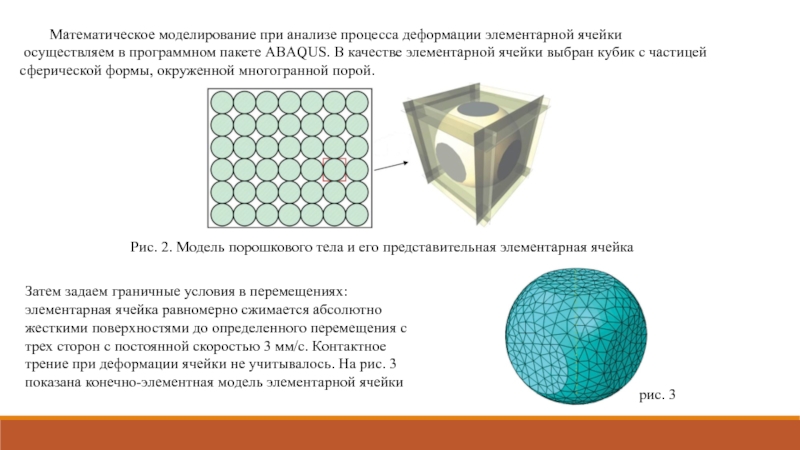
Слайд 14 Математическое моделирование при анализе процесса деформации элементарной ячейки
осуществляем в программном
Рис. 2. Модель порошкового тела и его представительная элементарная ячейка
Затем задаем граничные условия в перемещениях: элементарная ячейка равномерно сжимается абсолютно жесткими поверхностями до определенного перемещения с трех сторон с постоянной скоростью 3 мм/с. Контактное трение при деформации ячейки не учитывалось. На рис. 3 показана конечно-элементная модель элементарной ячейки
рис. 3
Слайд 15Для построения кривых предельного состояния порошковых материалов использовано условие текучести, заданное
Исследуя уравнение (1) на экстремум мы можем найти предел уплотнения и пластический сдвиг.