- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Раздел 2. Термодинамика поверхностных явлений презентация
Содержание
- 1. Раздел 2. Термодинамика поверхностных явлений
- 2. Любая термодинамическая система стремиться уменьшить свою поверхностную
- 3. Поверхностное натяжение Физический смысл поверхностного натяжения рМ – внутримолекулярное давление
- 4. Энергетическое определение поверхностного натяжения Поверхностное натяжение (σ)
- 5. Термодинамическое определение поверхностного натяжения При постоянных
- 6. Единицы измерения поверхностного натяжения Энергетическая единица измерения
- 7. Влияние различных факторов на величину поверхностного натяжения
- 8. Зависимость поверхностного натяжения от полярности (диэлектрической проницаемости)
- 9. Температура Т.к. с ростом температуры расстояние
- 10. Природа граничащих фаз Поверхностное натяжение на границе
- 11. Влияние природы и концентрации растворенного вещества на
- 12. Межмолекулярные и межфазные взаимодействия
- 13. Когезия Когезия – притяжение атомов или молекул
- 14. Адгезия Адгезия –
- 15. Растекание одной жидкости по поверхности другой
- 16. Смачивание Смачивание (адгезия жидкости) – взаимодействие жидкости
- 17. Анализ уравнения Юнга 1. Если σТГ>
- 18. Правило: лучше смачивает поверхность та жидкость, которая
- 19. Связь краевого угла смачивания с работой адгезии
- 20. Влияние шероховатости на смачивание Поверхность реальных
- 21. Флотация Флотация - метод обогащения полезных ископаемых,
- 22. Особенности искривленной поверхности раздела фаз
- 23. Важное качество дисперсных систем, связанное с раздробленностью
- 24. Уравнение Лапласа (вывод) В результате искривления
- 25. Для сферических частиц: Для частиц цилиндрической
- 26. Кривизна поверхности может быть положительной и отрицательной.
- 27. Капиллярное поднятие и опускание жидкости При смачивании
- 28. Несмачивание (θ > 90°), образуется выпуклый мениск,
- 29. При равновесии избыточное лапласовское давление равно гидростатическому
- 30. Капиллярным поднятием жидкостей объясняется ряд известных процессов
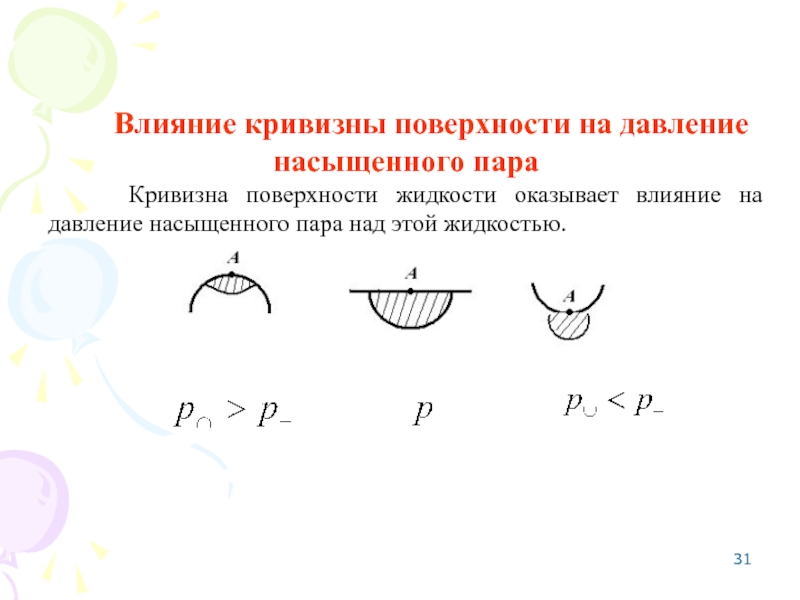
- 31. Влияние кривизны поверхности на давление насыщенного пара
- 32. Уравнения Томсона – Кельвина (вывод) Приращение энергии
- 33. С другой стороны в процессе испарения (Т=const)
- 34. Для сферической поверхности: Аналогично, для цилиндрической поверхности: Уравнения Томсона – Кельвина
- 35. Капиллярная конденсация При отрицательной
- 36. Изотермическая перегонка При положительной
- 37. Влияние дисперсности (кривизны поверхности) на различные физико-химические
- 38. 2. Связь дисперсности с константой равновесия Степень
- 39. 3. Влияние дисперсности на температуру фазовых переходов
- 40. Заменим:
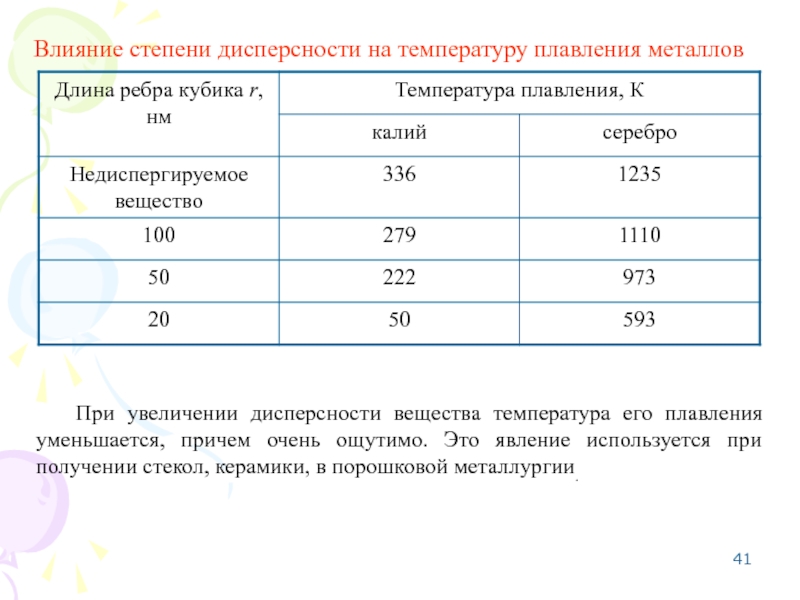
- 41. Влияние степени дисперсности на температуру плавления металлов
- 42. Методы определения поверхностного натяжения Методы бывают:
- 43. Сталагмометрический метод (метод счета капель) При вытекании
- 44. Статические методы Метод поднятия жидкости в капилляре
Слайд 2Любая термодинамическая система стремиться уменьшить свою поверхностную энергию.
Избыточная поверхностная энергия
уменьшения площади поверхности: сферическая форма капель (сглаживание поверхности), объединение частиц (коагуляция, агрегация, коалесценция).
уменьшения поверхностного натяжения: адсорбция, адгезия, смачивание, образование ДЭС;
Слайд 3Поверхностное натяжение
Физический смысл поверхностного натяжения
рМ – внутримолекулярное давление
Слайд 4Энергетическое определение поверхностного натяжения
Поверхностное натяжение (σ) – работа обратимого изотермического процесса,
Силовое определение поверхностного натяжения
Поверхностное натяжение – сила, направленная тангенциально (параллельно) к поверхности и приходящаяся на единицу длины периметра, ограничивающего эту поверхность.
Физическая сущность – поверхностные молекулы стремятся уйти вглубь конденсированной фазы, тем самым, сжимая поверхность.
Слайд 5Термодинамическое определение поверхностного натяжения
При постоянных Т, р, ni, q имеем:
Поверхностное натяжение
Слайд 6Единицы измерения поверхностного натяжения
Энергетическая единица измерения – Дж/м2, силовая –
Для воды при 293 К:
Одна размерность легко выводится из другой:
СИ: Дж/м2 = Н∙м/м2 =Н/м
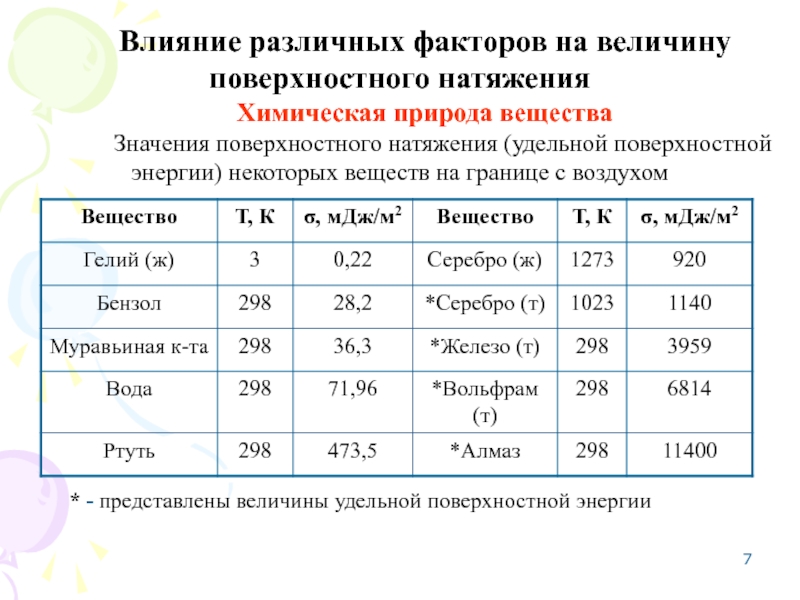
Слайд 7Влияние различных факторов на величину поверхностного натяжения
Химическая природа вещества
Значения поверхностного натяжения
* - представлены величины удельной поверхностной энергии
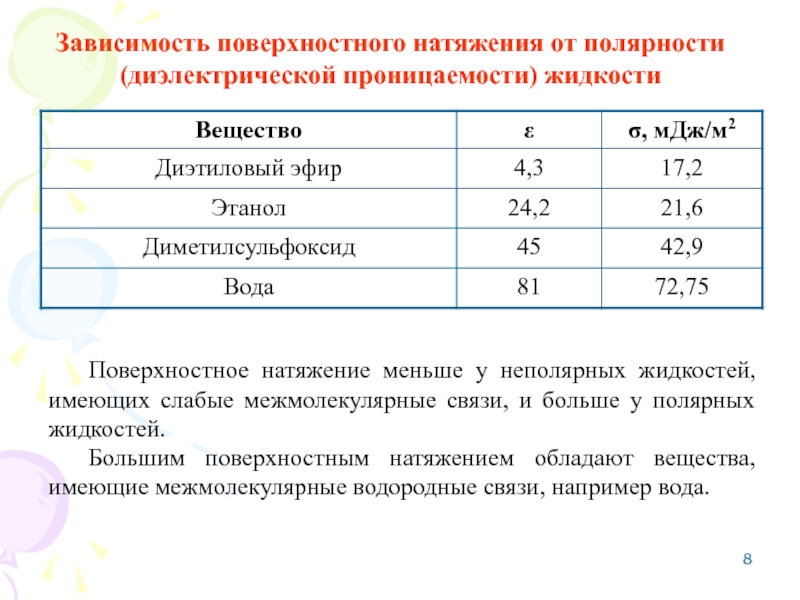
Слайд 8Зависимость поверхностного натяжения от полярности (диэлектрической проницаемости) жидкости
Поверхностное натяжение меньше у
Большим поверхностным натяжением обладают вещества, имеющие межмолекулярные водородные связи, например вода.
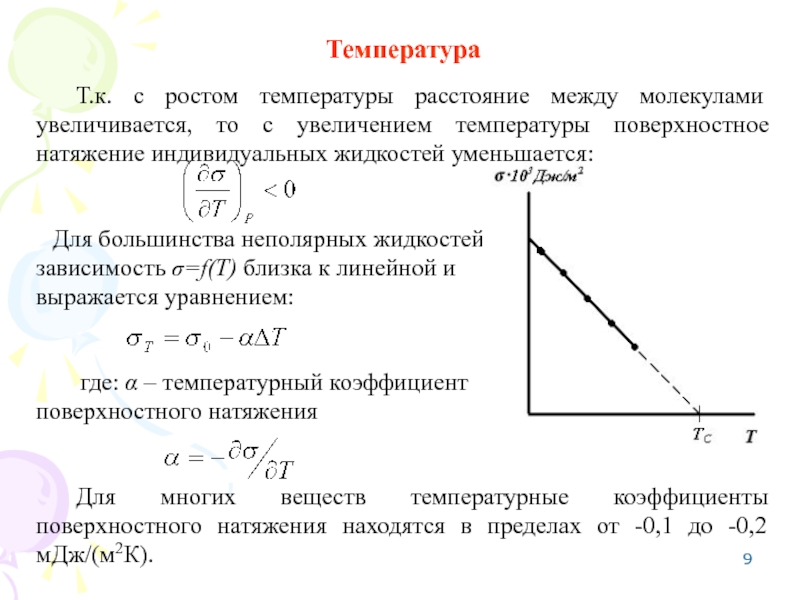
Слайд 9Температура
Т.к. с ростом температуры расстояние между молекулами увеличивается, то с увеличением
Для большинства неполярных жидкостей
зависимость σ=f(T) близка к линейной и
выражается уравнением:
где: α – температурный коэффициент
поверхностного натяжения
Для многих веществ температурные коэффициенты поверхностного натяжения находятся в пределах от -0,1 до -0,2 мДж/(м2К).
Слайд 10Природа граничащих фаз
Поверхностное натяжение на границе двух жидкостей зависит от
Межфазное натяжение на границе воды (ε = 81) с жидкими
органическими веществами.
Правило Ребиндера: чем больше разность полярностей жидкостей, тем больше поверхностное натяжение на границе их раздела.
Правило Антонова (1907): если жидкости ограниченно растворимы друг в друге, то поверхностное натяжение на границе ж1/ж2 равно разности между поверхностными натяжениями взаимно насыщенных жидкостей на границе их с воздухом или с их собственным паром:
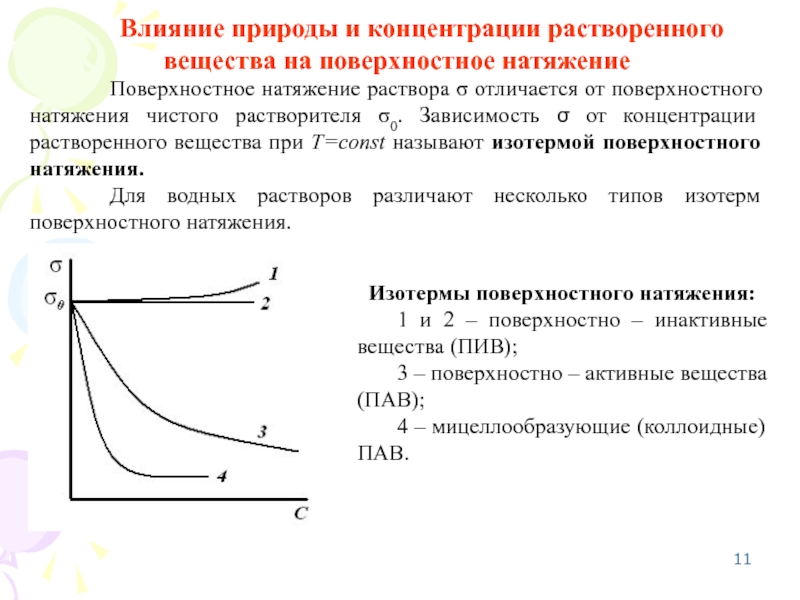
Слайд 11Влияние природы и концентрации растворенного вещества на поверхностное натяжение
Поверхностное натяжение раствора
Для водных растворов различают несколько типов изотерм поверхностного натяжения.
Изотермы поверхностного натяжения:
1 и 2 – поверхностно – инактивные вещества (ПИВ);
3 – поверхностно – активные вещества (ПАВ);
4 – мицеллообразующие (коллоидные) ПАВ.
Слайд 13Когезия
Когезия – притяжение атомов или молекул внутри отдельной фазы, обусловленное межмолекулярными
Работа когезии (Wк) - работа, затрачиваемая на разрыв тела по сечению, равному единице площади.
Величину Wк часто называют прочностью на разрыв или когезионной прочностью.
Слайд 14Адгезия
Адгезия – взаимодействие между разнородными конденсированными телами
Причина адгезии – молекулярное притяжение контактирующих веществ или их химическое взаимодействие.
Работа адгезии (WА) – работа, которую необходимо совершить для разделения двух контактирующих фаз.
Работу адгезии рассчитывают по уравнению Дюпре.
Применение адгезии: склеивание материалов, нанесение красок, покрытий и т.д.
Слайд 15Растекание одной жидкости по поверхности другой
Правило Гаркинса
Коэффициент растекания φ = WА – WК, если φ >0, то происходит растекание, если φ <0, растекание не происходит.
Способность к растеканию зависит от когезии наносимой жидкости.
Например, многие органические вещества растекаются по поверхности воды, а вода, как правило, не растекается на поверхности органических веществ.
Слайд 16Смачивание
Смачивание (адгезия жидкости) – взаимодействие жидкости с твердым или другим жидким
В условиях равновесия: σТГ = σТЖ + σЖГ ·cos θ
Отсюда:
Полученное соотношение называют законом Юнга.
Слайд 17Анализ уравнения Юнга
1. Если σТГ> σТЖ, то cos θ >
2. Если σТГ < σТЖ, то cos θ < 0, θ > 90° - краевой угол тупой - несмачивание. Пример: вода на парафине или тефлоне.
3. Если σТГ = σТЖ, то cos θ = 0, θ = 90° - граница между смачиваемостью и несмачиваемостью.
4. Если σТГ – σТЖ = σЖГ, то cos θ = 1 и θ = 0° - полное смачивание (растекание) – капля растекается в тонкую пленку. Пример: ртуть на поверхности свинца, очищенного от оксидной пленки.
Слайд 18Правило: лучше смачивает поверхность та жидкость, которая ближе по полярности к
По виду избирательного смачивания все твердые тела делят на две группы:
Гидрофильные (олеофобные) материалы – лучше смачиваются водой, чем неполярными углеводородами: кварц (θ = 0°), малахит (θ = 17°), силикаты, карбонаты, оксиды и гидроксиды металлов.
Гидрофобные (олеофильные) материалы - лучше смачиваются неполярными жидкостями, чем водой: парафин (θ = 106°), тефлон (θ = 120°), графит, уголь.
Слайд 19Связь краевого угла смачивания с работой адгезии
WA= σТГ+ σЖГ – σТЖ
Отсюда: σ ТГ – σТЖ= WА– σЖГ
Подставим в уравнение Юнга:
Если WА > σЖГ, то cos θ > 0 , смачивание.
Если WА < σЖГ, то cos θ < 0 , несмачивание.
Твердые тела лучше смачивают неполярные жидкости.
Слайд 20 Влияние шероховатости на смачивание
Поверхность реальных твердых тел шероховатая:
Sш > Sгл
смачивание
несмачивание (cosθ < 0), шероховатость улучшает несмачивание.
где: К – коэффициент шероховатости.
уравнение Венцеля - Дерягина
Слайд 21Флотация
Флотация - метод обогащения полезных ископаемых, основанное на их различной смачиваемости
Пример 1.: Порошок кварца и серы высыпали на поверхность воды. Какое явление можно ожидать, если краевой угол смачивания для кварца 0°, а для серы 78°.
Решение: Т.к. для кварца θ = 0° - полное смачивание, то кварц будет полностью смачиваться водой и будет оседать на дно емкости. Для серы θ < 90° - неполное смачивание – порошок серы образует суспензию на поверхности воды.
В случае пенной флотации через водную суспензию измельченной руды барботируют воздух, к пузырькам которого прилипают гидрофобные частицы ценного минерала (чистые металлы или их сульфиды), всплывающие затем на поверхность воды, и с образовавшейся пеной снимаются механически для дальнейшей переработки. Пустая порода (кварц, алюмосиликаты) хорошо смачивается водой и оседает во флотационных машинах.
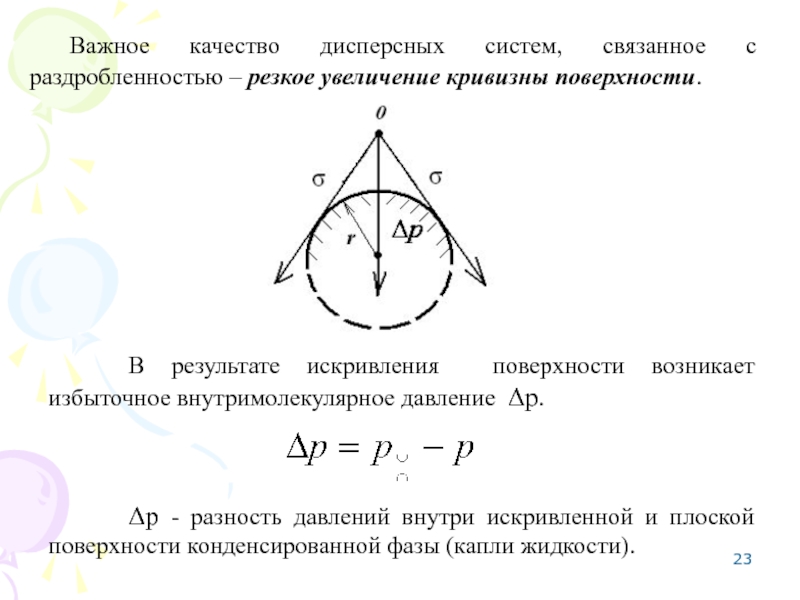
Слайд 23 Важное качество дисперсных систем, связанное с раздробленностью – резкое увеличение кривизны
В результате искривления поверхности возникает избыточное внутримолекулярное давление Δр.
Δр - разность давлений внутри искривленной и плоской поверхности конденсированной фазы (капли жидкости).
Слайд 24 Уравнение Лапласа (вывод)
В результате искривления поверхности совершается работа δW, которая
При постоянных Т, р, ni, q в условии равновесия dG = 0:
Тогда:
где: - кривизна поверхности.
Слайд 25Для сферических частиц:
Для частиц цилиндрической
формы:
Для частиц произвольной
формы:
уравнения
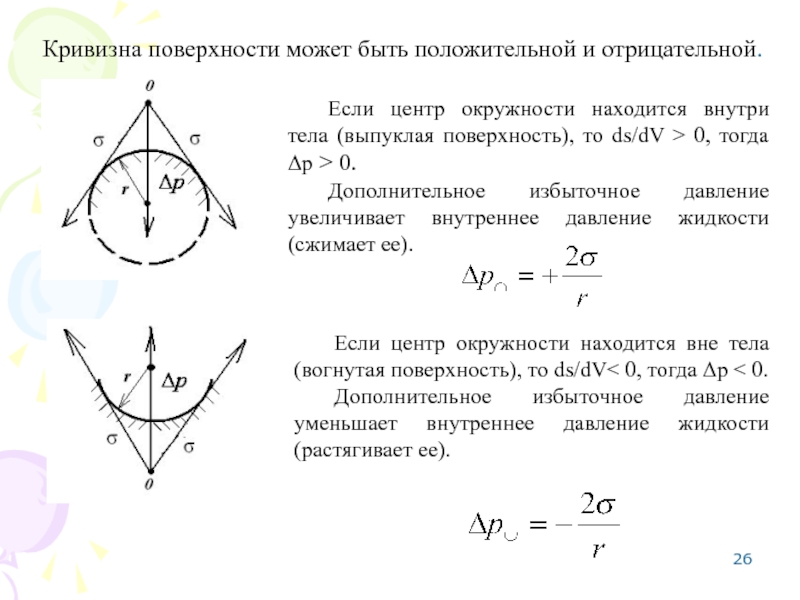
Слайд 26Кривизна поверхности может быть положительной и отрицательной.
Если центр окружности находится
Дополнительное избыточное давление увеличивает внутреннее давление жидкости (сжимает ее).
Если центр окружности находится вне тела (вогнутая поверхность), то ds/dV< 0, тогда Δр < 0.
Дополнительное избыточное давление уменьшает внутреннее давление жидкости (растягивает ее).
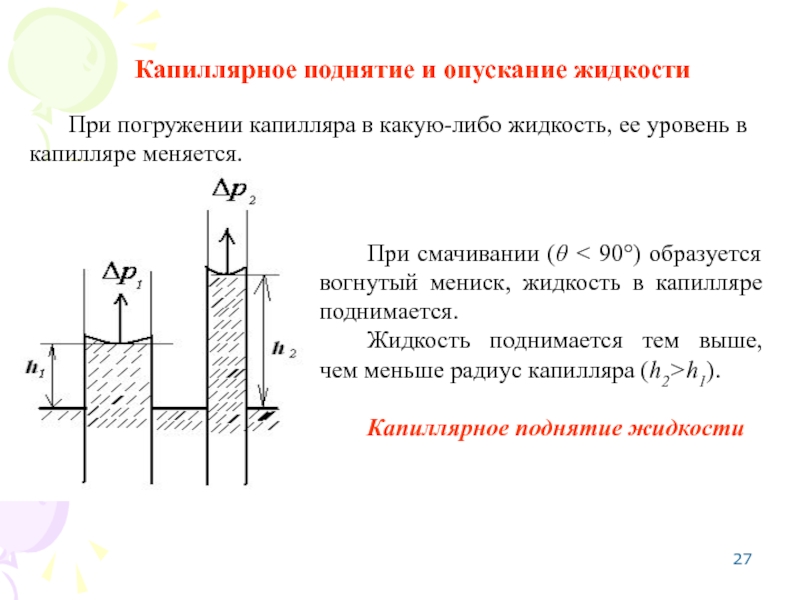
Слайд 27Капиллярное поднятие и опускание жидкости
При смачивании (θ < 90°) образуется вогнутый
Жидкость поднимается тем выше, чем меньше радиус капилляра (h2>h1).
Капиллярное поднятие жидкости
При погружении капилляра в какую-либо жидкость, ее уровень в капилляре меняется.
.
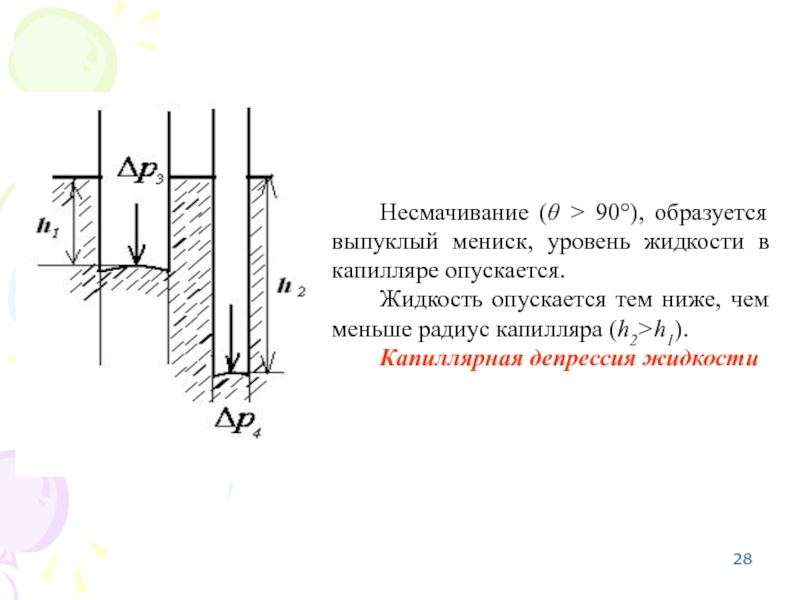
Слайд 28Несмачивание (θ > 90°), образуется выпуклый мениск, уровень жидкости в капилляре
Жидкость опускается тем ниже, чем меньше радиус капилляра (h2>h1).
Капиллярная депрессия жидкости
Слайд 29 При равновесии избыточное лапласовское давление равно гидростатическому давлению столба жидкости высотой
, отсюда
Высоту капиллярного поднятия жидкости можно вычислить:
уравнение Жюрена
где: r - радиус кривизны; R – радиус капилляра.
Слайд 30Капиллярным поднятием жидкостей объясняется ряд известных процессов и явлений:
поднятие грунтовых
пропитка бумаги и тканей – поднятие жидкости в порах;
водонепроницаемость тканей – ткани пропитывают веществами, которые вода не смачивает – капиллярная депрессия;
питание растений (деревьев) – подъем воды из почвы по волокнам древесины;
процессы кровообращения в кровеносных сосудах и т.д.
Слайд 31Влияние кривизны поверхности на давление насыщенного пара
Кривизна поверхности жидкости оказывает влияние
Слайд 32Уравнения Томсона – Кельвина (вывод)
Приращение энергии Гиббса в результате искривления поверхности:
При
где: Vm – мольный объем жидкости.
Тогда:
, или в интегральной форме:
Подставим в уравнение (1) уравнение Лапласа, получим:
для частиц сферической формы
для частиц цилиндрической формы
Слайд 33 С другой стороны в процессе испарения (Т=const) в случае искривленной поверхности:
Приравняем уравнение (4) к уравнению (2), для сферической поверхности получим:
Слайд 34Для сферической поверхности:
Аналогично, для цилиндрической поверхности:
Уравнения Томсона – Кельвина
Слайд 35Капиллярная конденсация
При отрицательной кривизне (вогнутая поверхность), давление насыщенного пара будет меньше
С уменьшением радиуса кривизны r, давление насыщенного пара будет уменьшаться:
Вывод: чем уже капилляр, тем меньше давление насыщенного пара.
Рекуперация – возвращение газообразных продуктов производства, потерянных в технологическом цикле, вновь в производство: на тонкопористых сорбентах газообразные продукты конденсируются при значительно более низких давлениях, чем на поверхности.
Слайд 36Изотермическая перегонка
При положительной кривизне (выпуклая поверхность) давление насыщенного пара будет больше,
С уменьшением радиуса кривизны давление насыщенного пара над выпуклой поверхностью будет увеличиваться:
Вывод: давление насыщенного пара над мелкими каплями жидкости будет всегда выше, чем над крупными.
Процесс изотермической перегонки является причиной выпадения атмосферных осадков (дождя); образования сталактитов и сталагмитов, образование вторичных рудных месторождений.
Слайд 37Влияние дисперсности (кривизны поверхности) на различные физико-химические процессы
1. Влияние дисперсности на
Реакционная способность вещества определяется изменением энергии Гиббса. Приращение энергии Гиббса в результате изменения дисперсности системы ΔGд при Т=соnst запишется:
или в интегральной форме
Для сферической выпуклой поверхности
Тогда:
Величина ΔGд показывает, на сколько изменилась энергия Гиббса в результате раздробленности дисперсной фазы.
Частицы с искривленной поверхностью приобретают дополнительную свободную энергию и обладают повышенной реакционной способностью, что оказывает большое влияние на интенсификацию различных процессов, в том числе и технологических.
Слайд 382. Связь дисперсности с константой равновесия
Степень дисперсности вещества влияет на равновесие
где: - приращение энергии Гиббса, обусловленное дисперсностью, К и Кд – константы равновесия реакции с учетом недиспергированных и диспергированных веществ.
Вывод: повышение дисперсности конечных или исходных веществ приводит к сдвигу равновесия химической реакции и к изменению константы равновесия, т.е. дисперсность влияет на равновесие подобно влиянию температуры и давления.
Пример:
Золото не взаимодействует с соляной кислотой, а коллоидное золото в ней растворяется.
Серебро, практически не растворимое в обычном состоянии, проявляет бактерицидное действие в высокодисперсном состоянии (препараты колларгол, протаргол).
Слайд 393. Влияние дисперсности на температуру фазовых переходов
С изменением дисперсности меняется температура
При постоянном давлении изменение энергии Гиббса, связанное с изменением дисперсности в соответствии с объединенными уравнениями первого и второго начал термодинамики запишется:
или в интегральном виде: (1)
где:
Тд – температура фазового перехода вещества в диспергированном состоянии, Т - температура фазового перехода вещества в макросостоянии.
Изменение энергии Гиббса через уравнение Лапласа для сферической поверхности запишется:
Приравняем уравнения (1) и (2), получим:
Из второго начала термодинамики:
Выразим ΔТ :
Слайд 40 Заменим:
Тогда получим:
где: ΔТ - изменение температуры при фазовом переходе при диспергировании.
Из уравнения следует, что при ΔНф.п.>0 (плавление и испарение), с уменьшением размера частиц r изменение температуры фазового перехода вещества в диспергируемом и макросостоянии ΔТ увеличивается:
Изменение температуры фазового перехода с изменением дисперсности тем больше, чем выше температура фазового перехода, больше поверхностное натяжение и меньше теплота фазового перехода. Поэтому для тугоплавких веществ наблюдается более сильный эффект понижения температуры плавления с постом дисперсности.
Слайд 41Влияние степени дисперсности на температуру плавления металлов
При увеличении дисперсности вещества температура
Слайд 42Методы определения поверхностного натяжения
Методы бывают: динамические и статические.
Метод наибольшего давления
Метод основан на измерении избыточного внутримолекулярного давления Δр, возникающего в жидкости в момент проскока газового пузырька. По уравнению Лапласа: Δр=2σ/r.
Измерения проводят относительным способом: находят наибольшее давление пузырька газа в стандартной жидкости и в исследуемом растворе:
Слайд 43Сталагмометрический метод (метод счета капель)
При вытекании жидкости из капилляра сталагмометра вес
Поверхностное натяжение жидкости будет равно:
Для каждого сталагмометра:
Чтобы исключить характеристики сталагмометра, подсчитывают число капель исследуемой и стандартной жидкостей:
Слайд 44Статические методы
Метод поднятия жидкости в капилляре
В основе лежит уравнение Жюрена:
На
Отсюда поверхностное натяжение жидкости будет равно: