- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Равновесие плоской системы параллельных сил презентация
Содержание
- 1. Равновесие плоской системы параллельных сил
- 2. РАВНОВЕСИЕ ПЛОСКОЙ СИСТЕМЫ ПАРАЛЛЕЛЬНЫХ СИЛ Пусть все
- 3. Из условия следуют две формы аналитических
- 4. Основная форма условий равновесия Для равновесия
- 5. Вторая форма условий равновесия: Для равновесия
- 7. РАСПРЕДЕЛЕННЫЕ НАГРУЗКИ равномерно распределенная вдоль прямой
- 8. Неравномерно распределенная нагрузка. Параллельные силы
- 9. РАВНОВЕСИЕ СИСТЕМЫ ТЕЛ Связи между частями
- 10. Для определения внутренних и внешних реакций связей
- 11. При действии на трех шарнирную арку
- 12. Статически определимые системы тел Системы тел (тело),
- 14. Проверка решения задачи Для проверки решения задачи
- 15. Графическая проверка Строят в масштабе силовой
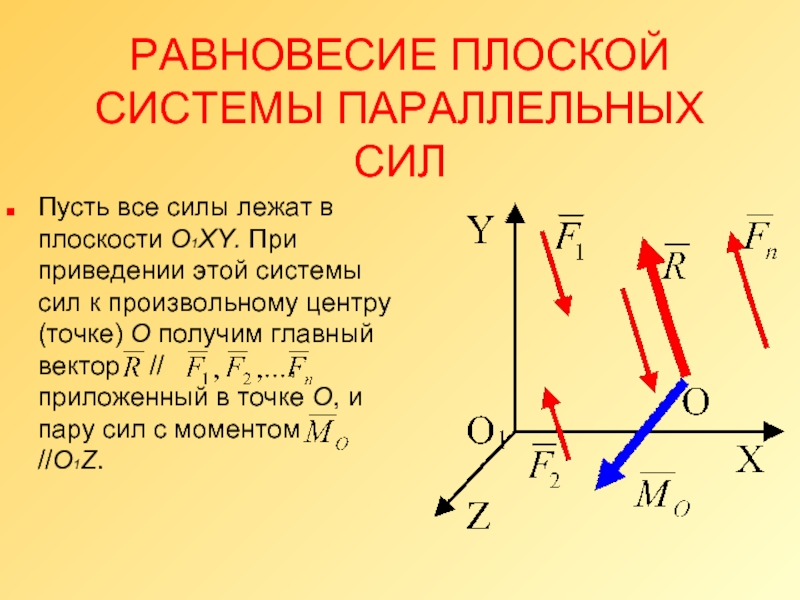
Слайд 2РАВНОВЕСИЕ ПЛОСКОЙ СИСТЕМЫ ПАРАЛЛЕЛЬНЫХ СИЛ
Пусть все силы лежат в плоскости О1XY.
Слайд 3Из условия
следуют две формы аналитических условий равновесия
плоской системы параллельных сил.
Расположим ось О1Y параллельно силам тогда вектор перпендикулярен плоскости О1XY и его можно считать величиной алгебраической
Из условия
следуют две формы аналитических условий равновесия
плоской системы параллельных сил.
Слайд 4Основная форма условий равновесия
Для равновесия плоской системы параллельных сил необходимо
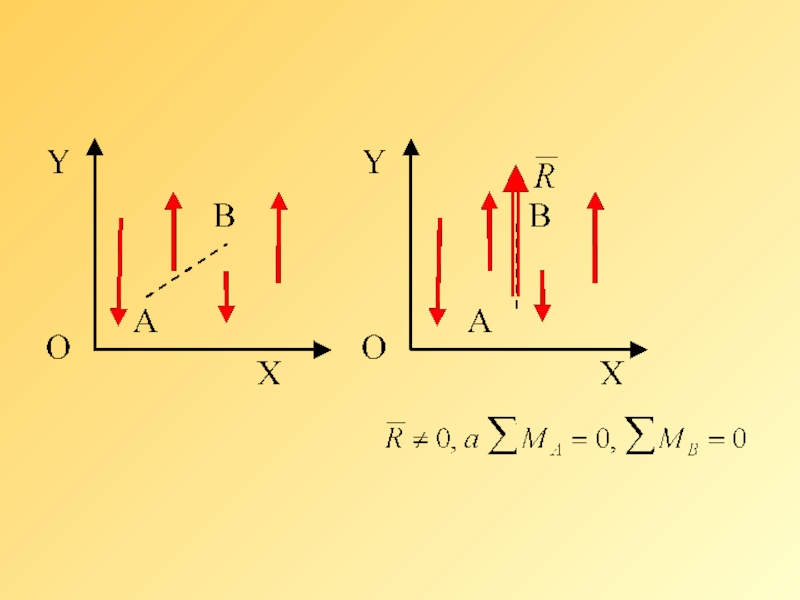
Слайд 5Вторая форма условий равновесия:
Для равновесия плоской системы параллельных сил необходимо
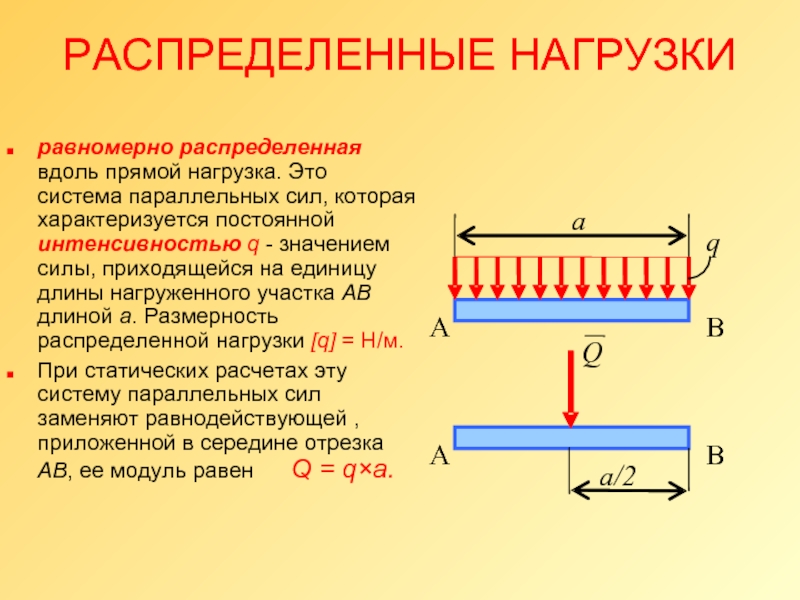
Слайд 7РАСПРЕДЕЛЕННЫЕ НАГРУЗКИ
равномерно распределенная вдоль прямой нагрузка. Это система параллельных сил,
При статических расчетах эту систему параллельных сил заменяют равнодействующей , приложенной в середине отрезка АВ, ее модуль равен Q = q×a.
Слайд 8
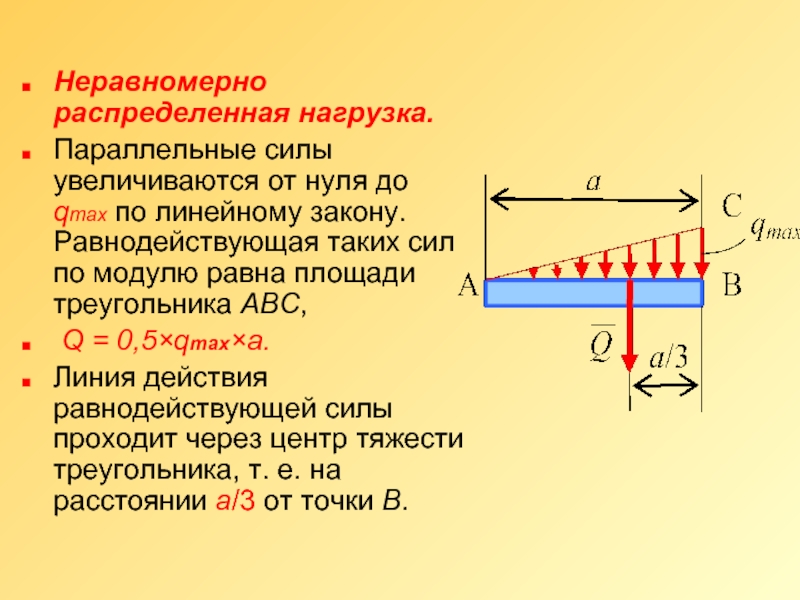
Неравномерно распределенная нагрузка.
Параллельные силы увеличиваются от нуля до qmax по
Q = 0,5×qmax×a.
Линия действия равнодействующей силы проходит через центр тяжести треугольника, т. е. на расстоянии a/3 от точки В.
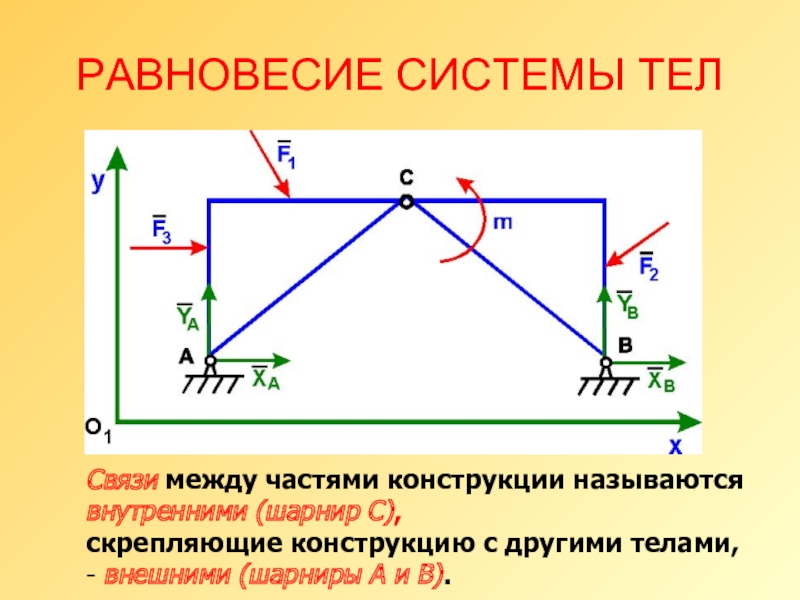
Слайд 9РАВНОВЕСИЕ СИСТЕМЫ ТЕЛ
Связи между частями конструкции называются внутренними (шарнир С),
скрепляющие конструкцию с другими телами, - внешними (шарниры А и В).
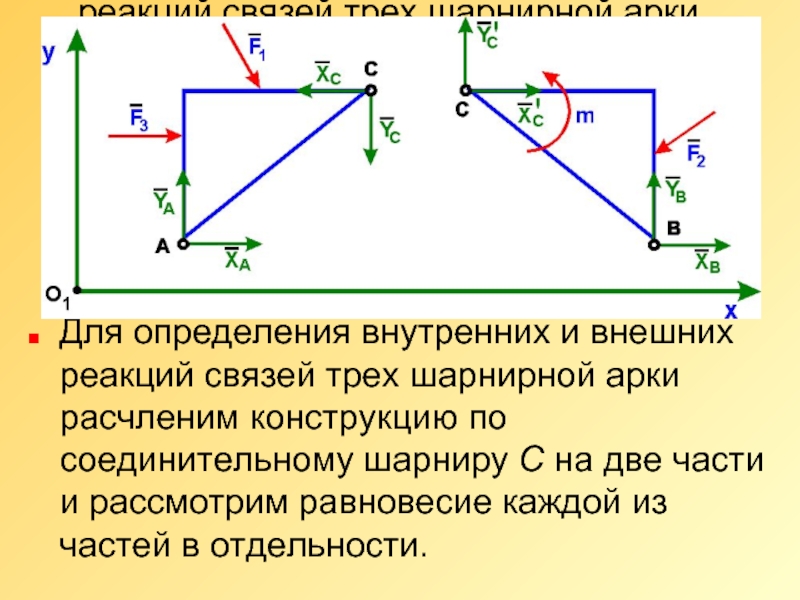
Слайд 10Для определения внутренних и внешних реакций связей трех шарнирной арки расчленим
Для определения внутренних и внешних реакций связей трех шарнирной арки расчленим конструкцию по соединительному шарниру С на две части и рассмотрим равновесие каждой из частей в отдельности.
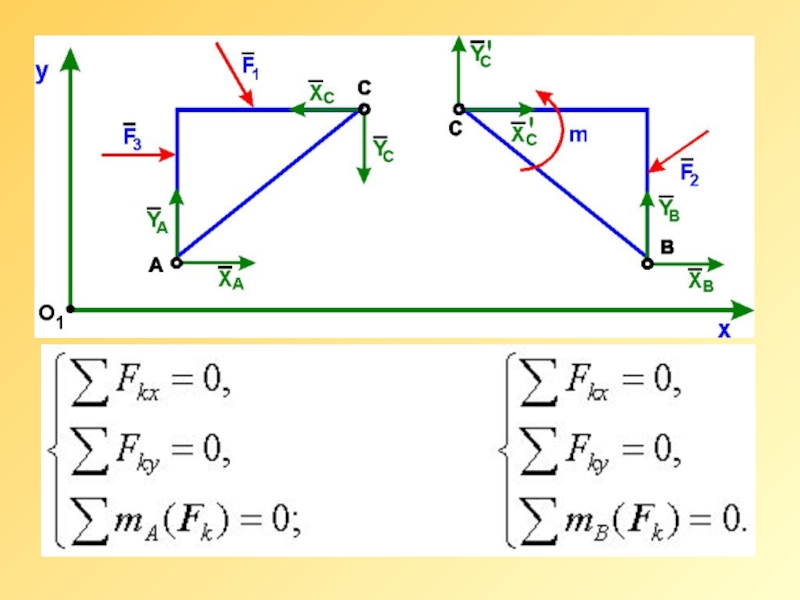
Слайд 11
При действии на трех шарнирную арку заданной произвольной плоской системы сил
Слайд 12Статически определимые системы тел
Системы тел (тело), для которых число неизвестных реакций
Слайд 14Проверка решения задачи
Для проверки решения задачи считают всю конструкцию отвердевшей (принцип
Слайд 15
Графическая проверка
Строят в масштабе силовой многоугольник. Если многоугольник замкнут, то задача
Аналитическая проверка
Составляют одно - два уравнения равновесия для конструкции в целом. Если проверочные уравнения равновесия обращаются в тождества, то задача решена верно.