- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Равнодействующие силы в пространстве. (Лекция 3) презентация
Содержание
- 1. Равнодействующие силы в пространстве. (Лекция 3)
- 2. ПЛАН 1) Возможные случаи приведения к равнодействующей
- 3. 1. Возможные случаи приведения к равнодействующей сил
- 4. Силы R,R" образуют уравновешенную систему сил. В
- 5. б) - система сил приводится к силе
- 7. 2. Условие равновесия пространственной системы сил. Произвольной
- 8. В аналитической форме: для равновесия произвольной
- 9. 3. Инварианты системы сил. Таким образом, главный
- 10. Из формулы (3.2) видно, скалярное произведение главного
- 11. 4. Условие равновесия системы сходящихся сил. Пусть
- 13. 5. Теорема о равновесии трех непараллельных сил.
- 14. Понятие о статике определимых и неопределимых задачах.
- 15. 6. Теорема Вариньона для системы сходящихся сил (теорема о моменте равнодействующей).
Слайд 2ПЛАН
1) Возможные случаи приведения к равнодействующей сил произвольно разложенных в пространстве.
2)
3) Инварианты системы сил.
4) Условие равновесия системы сходящихся сил в векторной форме. Аналитические условия равновесия системы сходящихся сил.
5) Теорема о равновесии трех непараллельных сил.
Понятие о статике определимых и неопределимых задачах.
6) Сложение трёх сил, не лежащих в одной плоскости.
Слайд 31. Возможные случаи приведения к равнодействующей сил произвольно разложенных в пространстве.
По
I)
Система сил приводится к одной силе – равнодействующей, при этом линия действия равнодействующей проходит через центр приведения.
II)
Исходную систему сил можно заменить двумя силами, образующими пару сил.
III)
Система сил приводится к силе и паре.
а) ,то есть - пара и сила лежат в одной плоскости.
Выбирая силы, составляющие пару
находим ее плечо ;
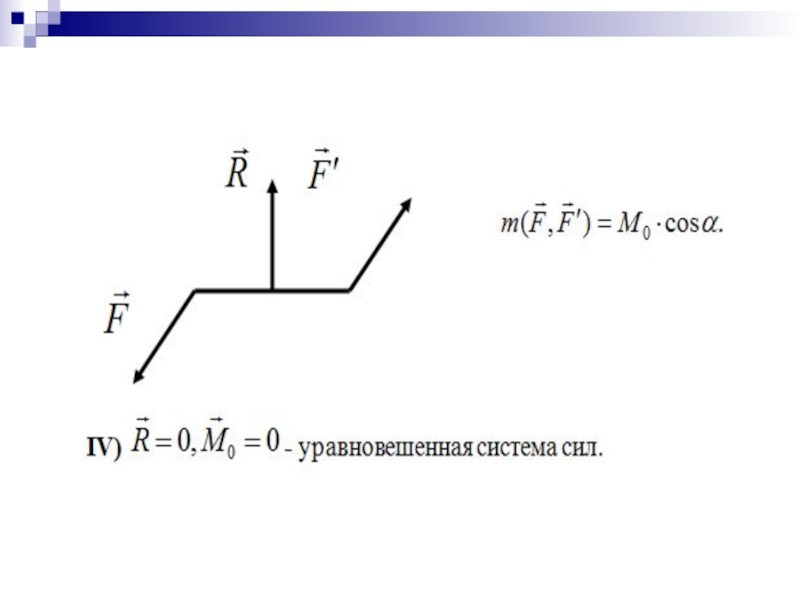
Слайд 4Силы R,R" образуют уравновешенную систему сил. В результате исходная система сил
{ }~{ }, которая проходит через т. О , отстоящую от центра приведения на расстоянии, равном отношению главного момента к главному вектору.
Этот случай всегда реализуется у плоской системы сил при отличных от нуля главном векторе и главном моменте.
Слайд 72. Условие равновесия пространственной системы сил.
Произвольной пространственной системой сил называется система
Согласно основной теоремы статики (теореме Пуансо), любую произвольную систему сил, действующих на твердое тело, можно заменить эквивалентной системой, состоящей из силы (главного вектора системы) и пары сил (главного момента сил).
Отсюда вытекает условие равновесия произвольной пространственной системы сил:
В геометрической форме: для равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы главный вектор и главный момент системы равнялись нулю.
Слайд 8
В аналитической форме: для равновесия произвольной пространственной системы сил необходимо и
Слайд 93. Инварианты системы сил.
Таким образом, главный вектор системы сил является векторным
Получим второй скалярный инвариант. Для этого умножим правую и левую части уравнения (3.1) скалярно на : (3.1)
получим: (3.2)
Т.к. смешанное произведение векторов, содержащих два одинаковых множителя R, равно нулю, т.е
Физические величины инвариантны относительно данного преобразования координат, если значения этих величин не меняются при переходе к другой системе координат.
Главный вектор для любого центра приведения выражается векторной суммой:
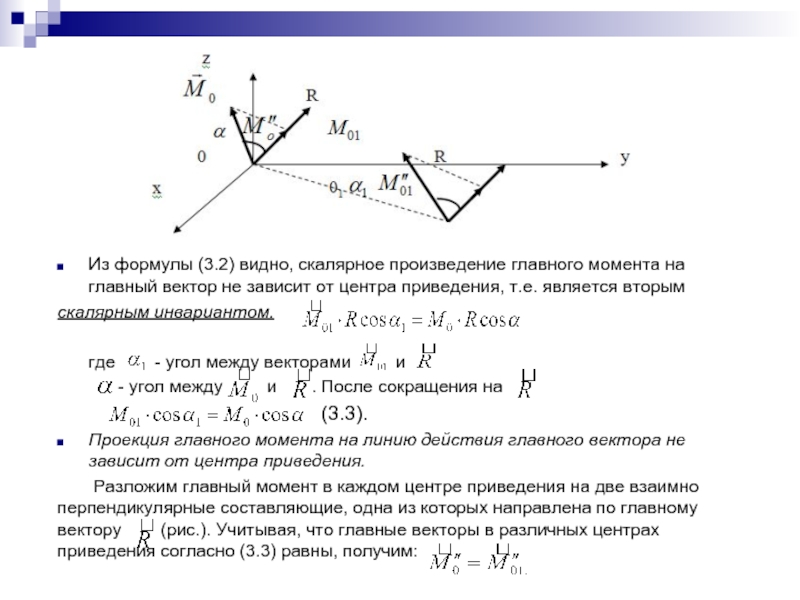
Слайд 10Из формулы (3.2) видно, скалярное произведение главного момента на главный вектор
скалярным инвариантом.
где - угол между векторами и
- угол между и . После сокращения на
(3.3).
Проекция главного момента на линию действия главного вектора не зависит от центра приведения.
Разложим главный момент в каждом центре приведения на две взаимно перпендикулярные составляющие, одна из которых направлена по главному вектору (рис.). Учитывая, что главные векторы в различных центрах приведения согласно (3.3) равны, получим:
Слайд 114. Условие равновесия системы сходящихся сил.
Пусть на абсолютно твердое тело действует
В проекциях на оси декартовых координат условие равновесия представляют так:
т.е. для равновесия системы сходящихся сил необходимо и достаточно, чтобы сумма проекций всех сил на каждую из осей координат была равна нулю. Для плоской системы сил в проекциях будут только два условия равновесия.
Геометрическое условие равновесия (3.5) означает следующее: поскольку для равновесия системы сходящихся сил необходимо и достаточно, чтобы равнодействующая равнялась нулю, то необходимо и достаточно, чтобы векторный многоугольник, построенный на этих силах, как на сторонах, был замкнут.
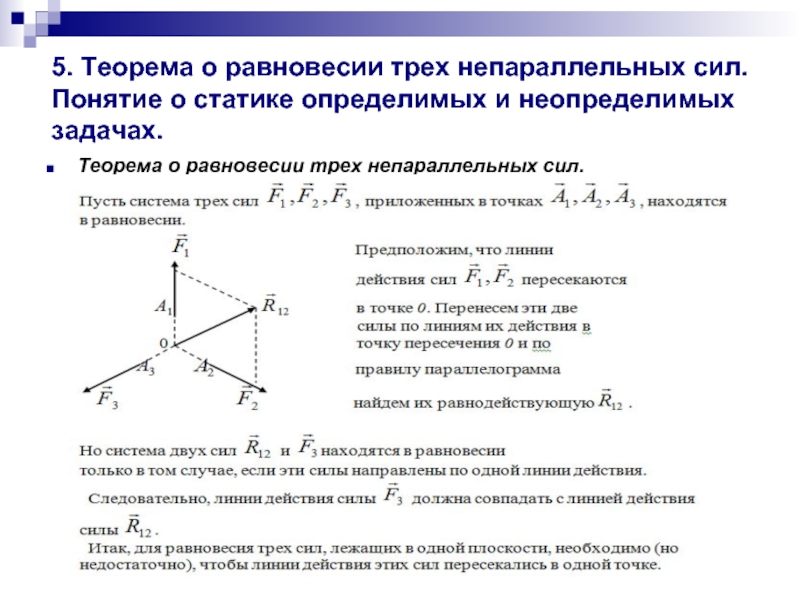
Слайд 135. Теорема о равновесии трех непараллельных сил. Понятие о статике определимых и
Теорема о равновесии трех непараллельных сил.
Слайд 14Понятие о статике определимых и неопределимых задачах.
Для любой плоской системы сил,
Независимые условия равновесия можно брать в трех различных формах. В случае пространственной системы сил, действующих на твердое тело, имеется шесть независимых условий равновесия. Следовательно, для любой пространственной системы сил из условий равновесия можно найти не более 6 неизвестных.
Задачи, в которых число неизвестных не больше числа неизвестных условий равновесия для данной системы сил, приложенных к твердому телу, называется статистически определимыми.
В противном случае задачи статистически неопределимы.
Если система трех непараллельных сил находится в равновесии, то линии действия этих сил должны пересекаться в одной точке.