- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Рассеяние света малыми частицами презентация
Содержание
- 1. Рассеяние света малыми частицами
- 2. Основные понятия рассеяния на частице Все коэффициенты имеют размерность L-2, а факторы безразмерны
- 3. Рассеянное поле При рассеянии интересует поле на больших расстояниях от рассеивающей частицы
- 4. Оптическая теорема Соответственно, зная амплитудный коэффициент рассеяния можно определить все характеристики рассеяния
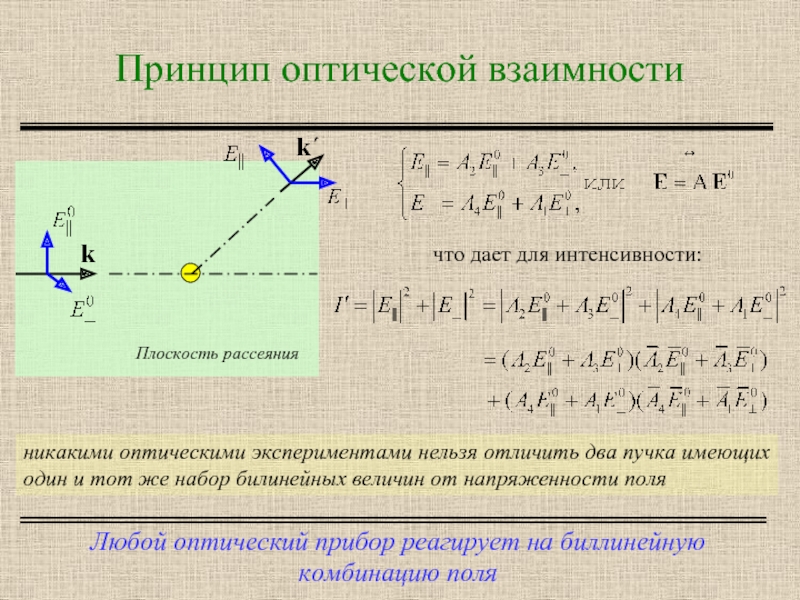
- 5. Принцип оптической взаимности Любой оптический прибор реагирует
- 6. Параметры Стокса (Stokes) 4 различных типа приемников:
- 7. Вектор-параметр Стокса Реакция любого оптического приемника выражается
- 8. Преобразование параметров Стокса В общем случае мутная (рассеяние + поглощение) среда является двулучепреломляющей и дихроичной
- 9. Теория Ми (Gustav Mie, Greifswald, 1908) По
- 10. Поле рассеянной волны Расчеты по формулам теории
- 11. Явление рассеяния Принцип локализации Debye: am и
Слайд 1Рассеяние света малыми частицами
☎: +7 (495) 763-5239 BudakVP@mpei.ru
Будак Владимир Павлович,
Национальный исследовательский университет
кафедра светотехники
Слайд 2Основные понятия рассеяния на частице
Все коэффициенты имеют размерность L-2,
а факторы безразмерны
Слайд 4Оптическая теорема
Соответственно, зная амплитудный коэффициент рассеяния можно определить все характеристики рассеяния
Слайд 5Принцип оптической взаимности
Любой оптический прибор реагирует на биллинейную комбинацию поля
никакими оптическими
Слайд 6Параметры Стокса (Stokes)
4 различных типа приемников: естественный, линейные вертикально и горизонтально,
Следовательно, можно определить различную комбинацию параметров, но всегда их будет 4, поскольку существуют
Слайд 7Вектор-параметр Стокса
Реакция любого оптического приемника выражается через вектор-параметр Стокса
Поляризация частично-когерентного света:
Все параметры Стокса имеют размерность яркости и соответствуют измерению яркомером с поляризационным фильтром: нейтральный, два скрещенных линейных (0º и 45º) и циркулярным
Параметры Стокса определяются для луча относительно некоторой плоскости – плоскость референции
Слайд 8Преобразование параметров Стокса
В общем случае мутная (рассеяние + поглощение) среда
является двулучепреломляющей
Слайд 9Теория Ми (Gustav Mie, Greifswald, 1908)
По сути решение Ми есть единственное
M – магнитные колебания: Er=0, Hr≠0; N – электрические: Er ≠ 0, Hr=0;
Слайд 10Поле рассеянной волны
Расчеты по формулам теории Ми до недавнего времени представляли
Слайд 11Явление рассеяния
Принцип локализации Debye: am и bm имеют сложный характер при
Для качественного анализа явления рассеяния можно представить, что рассеянная волна состоит из компонент:
отраженная
преломленная
дифракция
краевой эффект: распределение вперед
поверхностная волна: “рябь” на Qe(λ), точное рассеяние назад, глории