стержней
называются узлами
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Расчёт ферм презентация
Содержание
- 1. Расчёт ферм
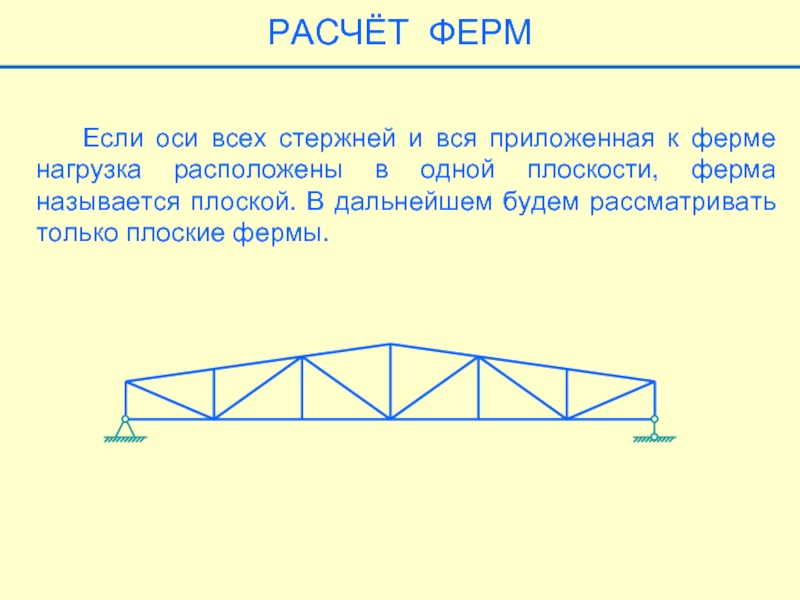
- 12. Если оси всех стержней и
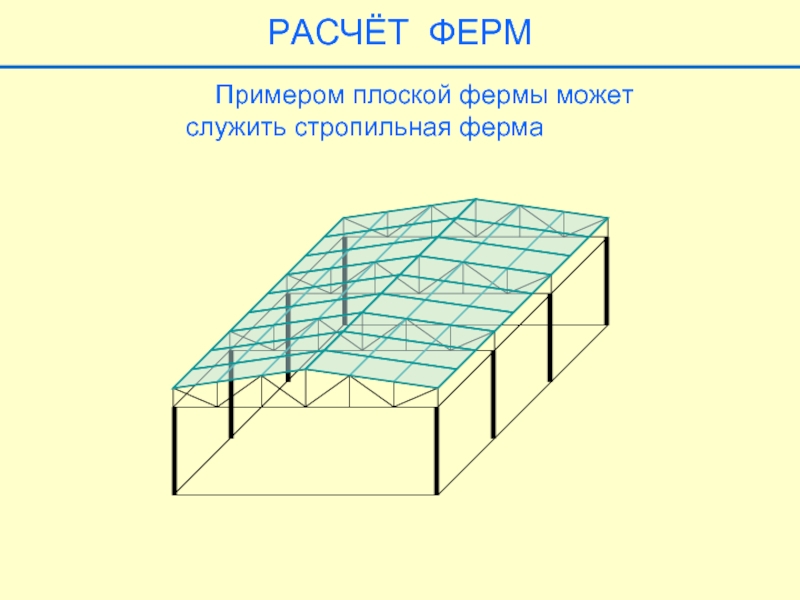
- 13. РАСЧЁТ ФЕРМ Примером плоской фермы может служить стропильная ферма
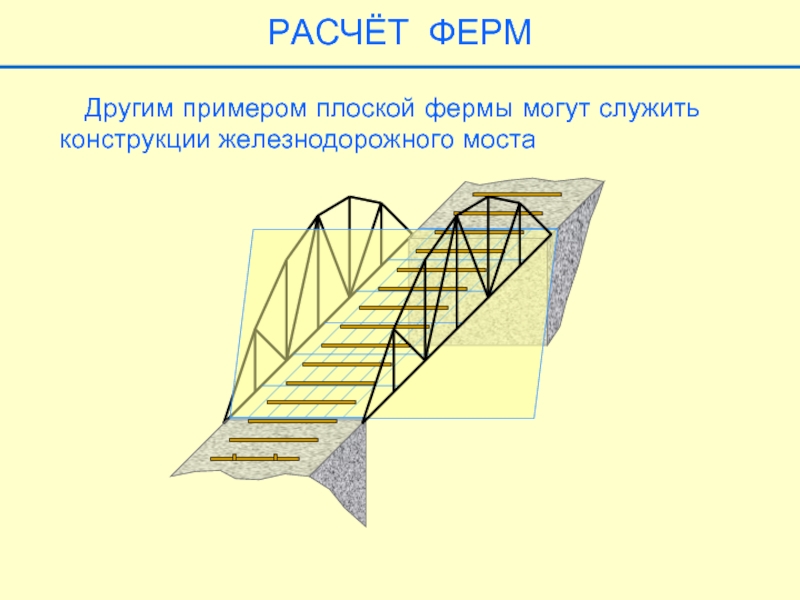
- 15. РАСЧЁТ ФЕРМ Другим примером плоской фермы могут служить конструкции железнодорожного моста
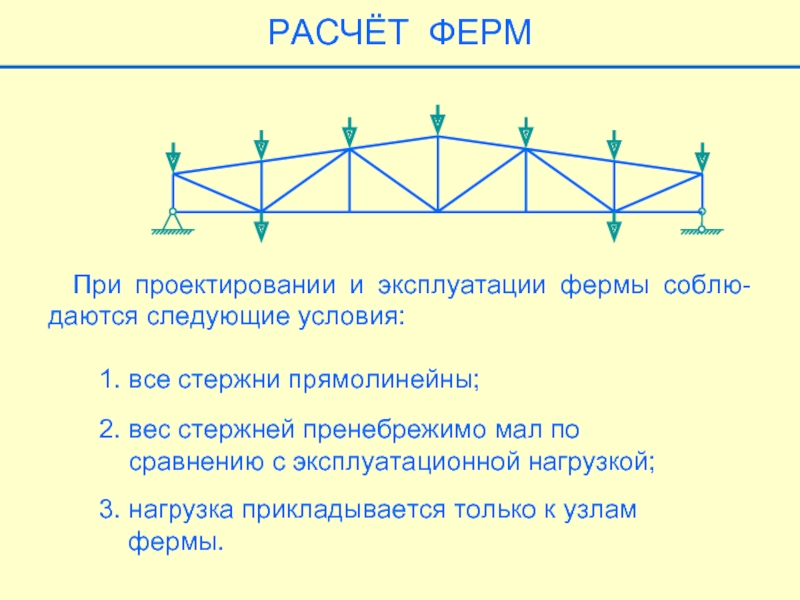
- 16. При проектировании и эксплуатации фермы соблю-даются
- 18. РАСЧЁТ ФЕРМ Эксплуатационная нагрузка через поперечные балки передаётся на узлы боковых ферм моста.
- 19. РАСЧЁТ ФЕРМ Эксплуатационная нагрузка
- 20. При соблюдении указанных условий усилиями,
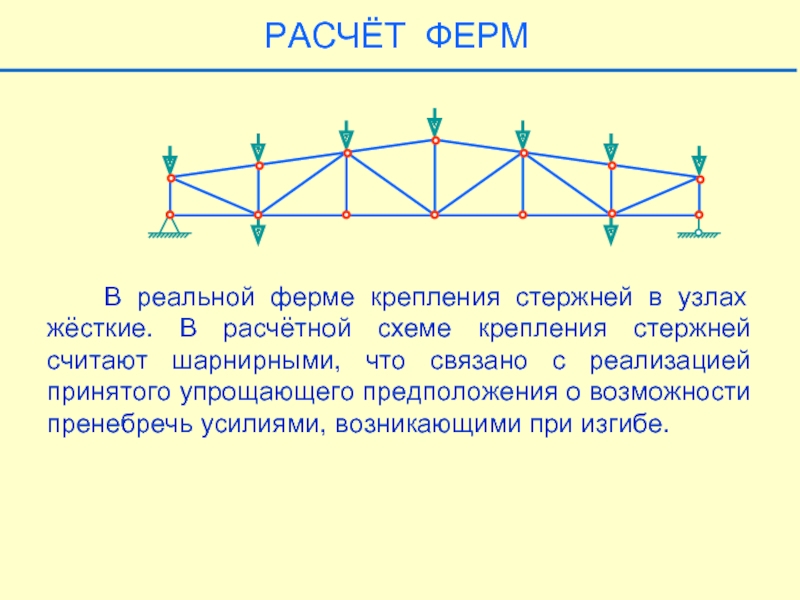
- 21. РАСЧЁТ ФЕРМ В реальной ферме
- 22. РАСЧЁТ ФЕРМ При соблюдении оговорённых
- 23. РАСЧЁТ ФЕРМ При соблюдении оговорённых
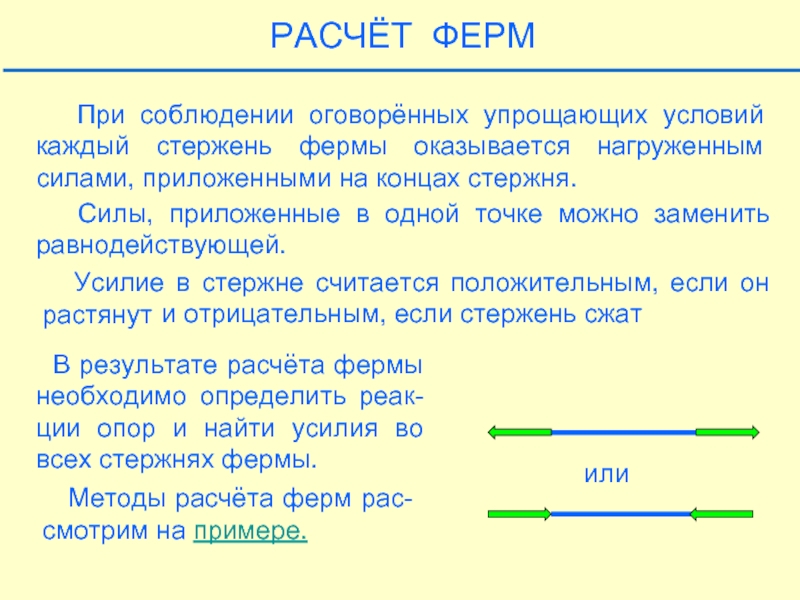
- 24. или РАСЧЁТ ФЕРМ
- 25. ? Метод вырезания узлов в
- 27. Чтобы убедиться в правильности полученного
- 28. Понятно, что результат проверки может быть разным. Возможны варианты. Первый вариант Второй вариант РАСЧЁТ ФЕРМ
- 29. ОПРЕДЕЛЕНИЕ УСИЛИЙ В СТЕРЖНЯХ ФЕРМЫ МЕТОДОМ
- 30. Метод сквозных сечений состоит в
- 31. Можно рассмотреть равновесие
- 32. РАСЧЁТ ФЕРМ Можно
- 33. РАСЧЁТ ФЕРМ Любая
- 34. Найдём минимальное число N стержней,
- 35. Найдём минимальное число N стержней,
- 36. Найдём минимальное число N стержней,
- 37. Найдём минимальное число N стержней,
- 38. Найдём минимальное число N стержней,
- 39. Найдём минимальное число N стержней,
- 40. Найдём минимальное число N стержней,
- 41. Найдём минимальное число N стержней,
- 42. Найдём минимальное число N стержней,
- 43. Найдём минимальное число N стержней,
- 44. УСЛОВИЕ СТАТИЧЕСКОЙ ОПРЕДЕЛИМОСТИ ФЕРМЫ
- 45. «Лишние» опоры –
Если оси всех стержней и вся приложенная к ферме нагрузка расположены в одной плоскости, ферма называется плоской. В дальнейшем будем рассматривать только плоские фермы. РАСЧЁТ ФЕРМ
Слайд 1РАСЧЁТ ФЕРМ
Фермой называется геометрически
неизменяемая конструкция, состоящая
из стержней. Места соединений
Слайд 12 Если оси всех стержней и вся приложенная к ферме
нагрузка расположены в одной плоскости, ферма называется плоской. В дальнейшем будем рассматривать только плоские фермы.
РАСЧЁТ ФЕРМ
Слайд 16 При проектировании и эксплуатации фермы соблю-даются следующие условия:
1. все стержни
прямолинейны;
2. вес стержней пренебрежимо мал по
сравнению с эксплуатационной нагрузкой;
3. нагрузка прикладывается только к узлам
фермы.
РАСЧЁТ ФЕРМ
Слайд 17
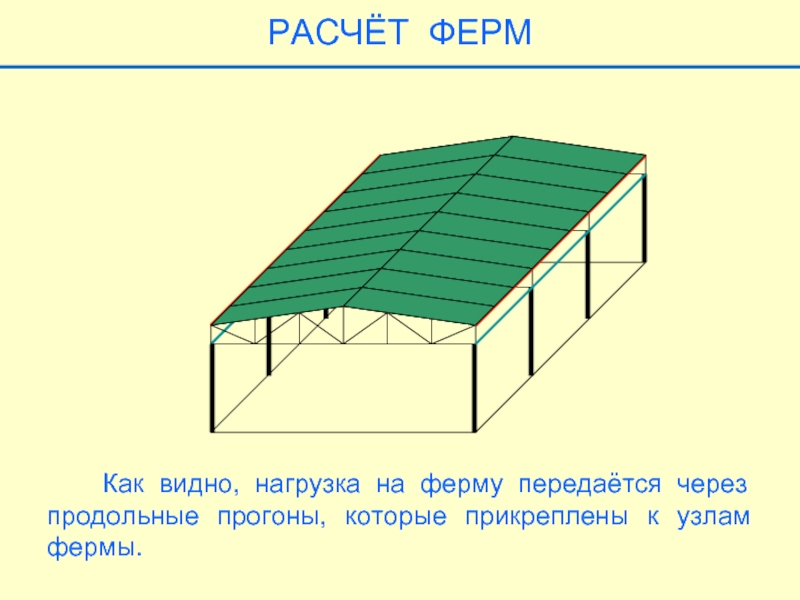
РАСЧЁТ ФЕРМ
Как видно, нагрузка на ферму передаётся через продольные
прогоны, которые прикреплены к узлам фермы.
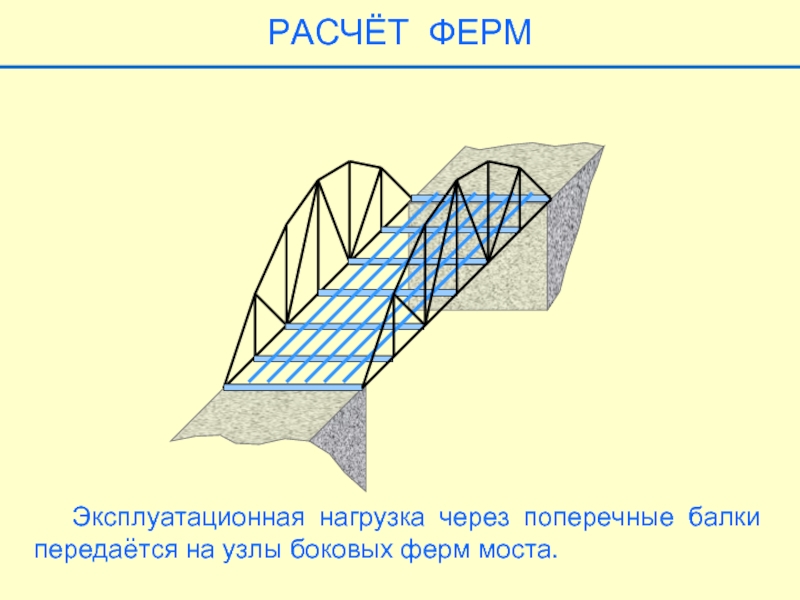
Слайд 18РАСЧЁТ ФЕРМ
Эксплуатационная нагрузка через поперечные балки передаётся на узлы
боковых ферм моста.
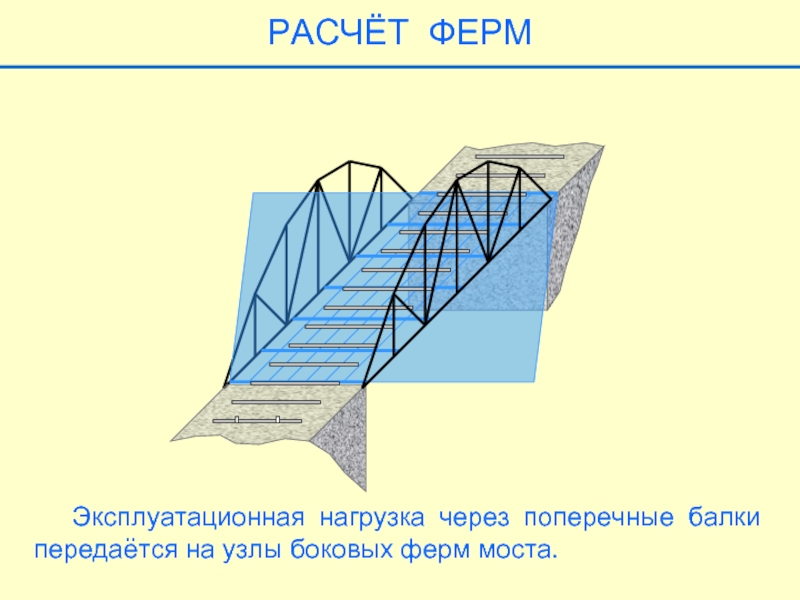
Слайд 19
РАСЧЁТ ФЕРМ
Эксплуатационная нагрузка через поперечные балки передаётся на узлы
боковых ферм моста.
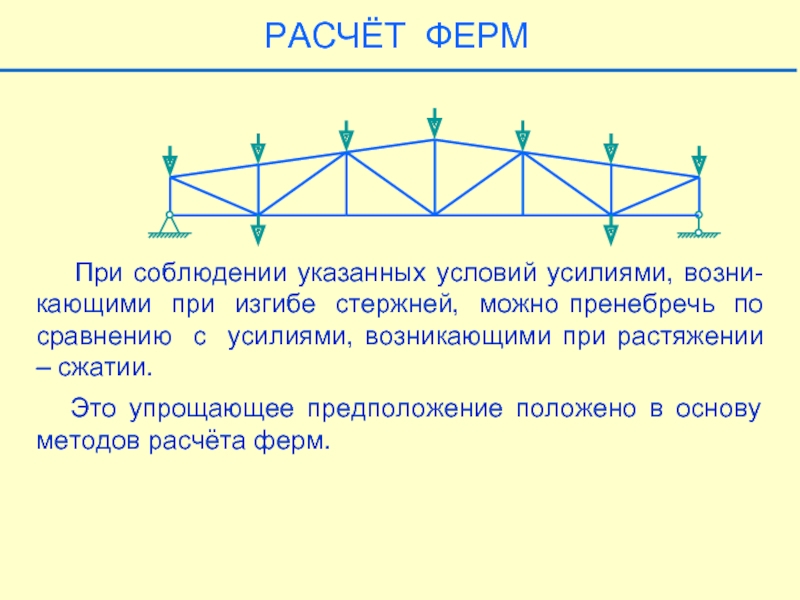
Слайд 20 При соблюдении указанных условий усилиями, возни-кающими при изгибе стержней,
можно пренебречь по сравнению с усилиями, возникающими при растяжении – сжатии.
Это упрощающее предположение положено в основу методов расчёта ферм.
РАСЧЁТ ФЕРМ
Слайд 21РАСЧЁТ ФЕРМ
В реальной ферме крепления стержней в узлах жёсткие.
В расчётной схеме крепления стержней считают шарнирными, что связано с реализацией принятого упрощающего предположения о возможности пренебречь усилиями, возникающими при изгибе.
Слайд 22РАСЧЁТ ФЕРМ
При соблюдении оговорённых упрощающих условий каждый стержень фермы
оказывается нагруженным силами, приложенными на концах стержня.
Слайд 23РАСЧЁТ ФЕРМ
При соблюдении оговорённых упрощающих условий каждый стержень фермы
оказывается нагруженным силами, приложенными на концах стержня.
Силы, приложенные в одной точке можно заменить равнодействующей.
Слайд 24
или
РАСЧЁТ ФЕРМ
При соблюдении оговорённых упрощающих условий каждый стержень фермы
оказывается нагруженным силами, приложенными на концах стержня.
Силы, приложенные в одной точке можно заменить равнодействующей.
Усилие в стержне считается положительным, если он растянут
и отрицательным, если стержень сжат
В результате расчёта фермы необходимо определить реак-ции опор и найти усилия во всех стержнях фермы.
Методы расчёта ферм рас-смотрим на примере.
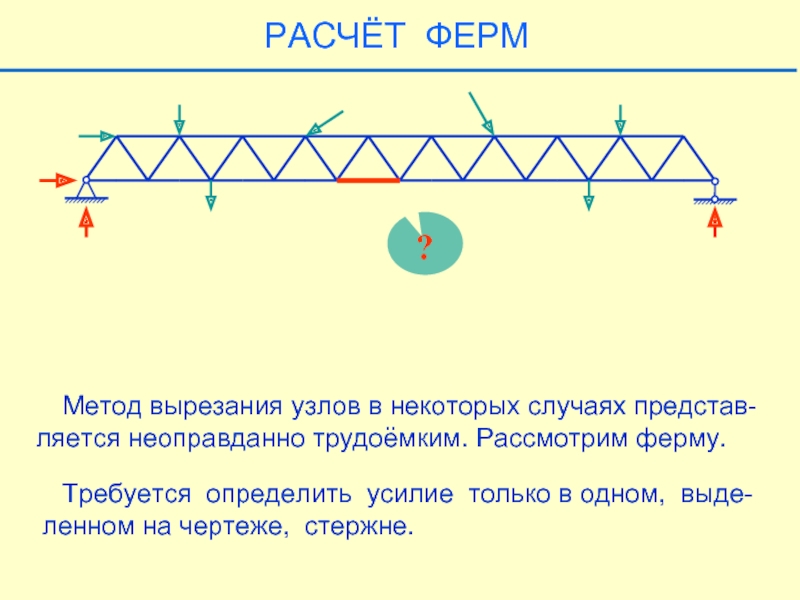
Слайд 25?
Метод вырезания узлов в некоторых случаях представ-
ляется неоправданно трудоёмким.
Рассмотрим ферму.
Требуется определить усилие только в одном, выде-ленном на чертеже, стержне.
РАСЧЁТ ФЕРМ
Слайд 26
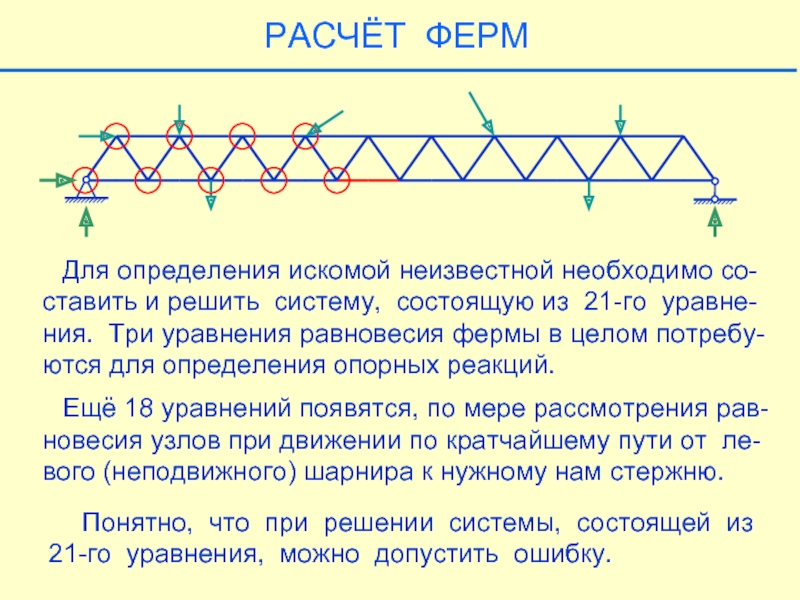
Для определения искомой неизвестной необходимо со-ставить и решить систему,
состоящую из 21-го уравне-ния. Три уравнения равновесия фермы в целом потребу-ются для определения опорных реакций.
Ещё 18 уравнений появятся, по мере рассмотрения рав-
новесия узлов при движении по кратчайшему пути от ле-
вого (неподвижного) шарнира к нужному нам стержню.
Понятно, что при решении системы, состоящей из 21-го уравнения, можно допустить ошибку.
РАСЧЁТ ФЕРМ
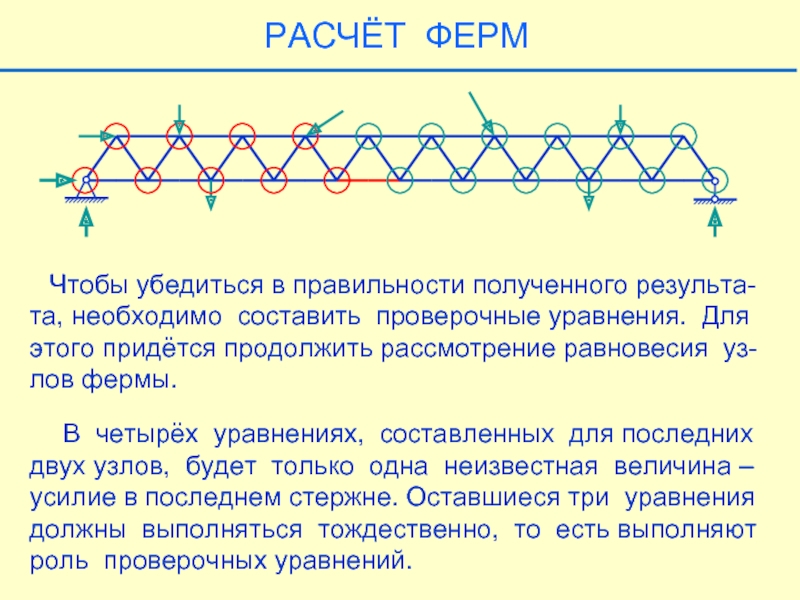
Слайд 27 Чтобы убедиться в правильности полученного результа-та, необходимо составить проверочные
уравнения. Для этого придётся продолжить рассмотрение равновесия уз-лов фермы.
В четырёх уравнениях, составленных для последних
двух узлов, будет только одна неизвестная величина –
усилие в последнем стержне. Оставшиеся три уравнения
должны выполняться тождественно, то есть выполняют
роль проверочных уравнений.
РАСЧЁТ ФЕРМ
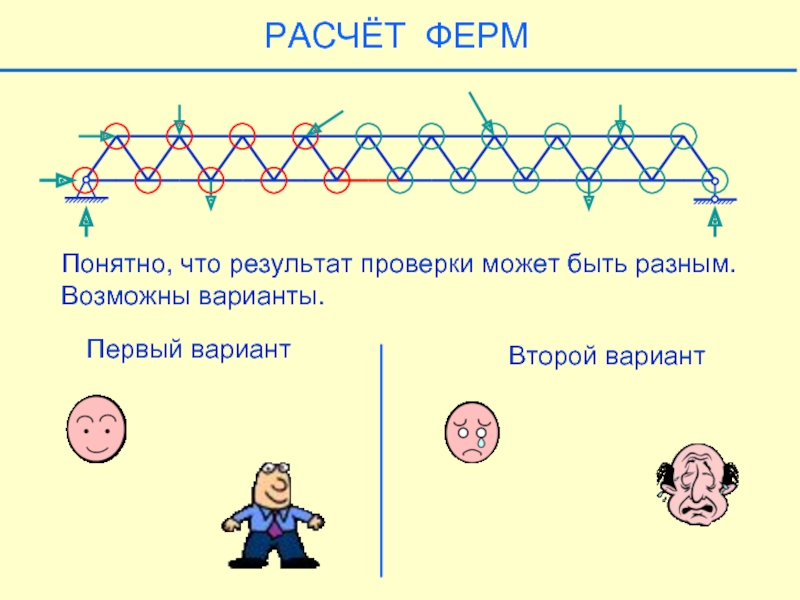
Слайд 28Понятно, что результат проверки может быть разным. Возможны варианты.
Первый вариант
Второй вариант
РАСЧЁТ
ФЕРМ
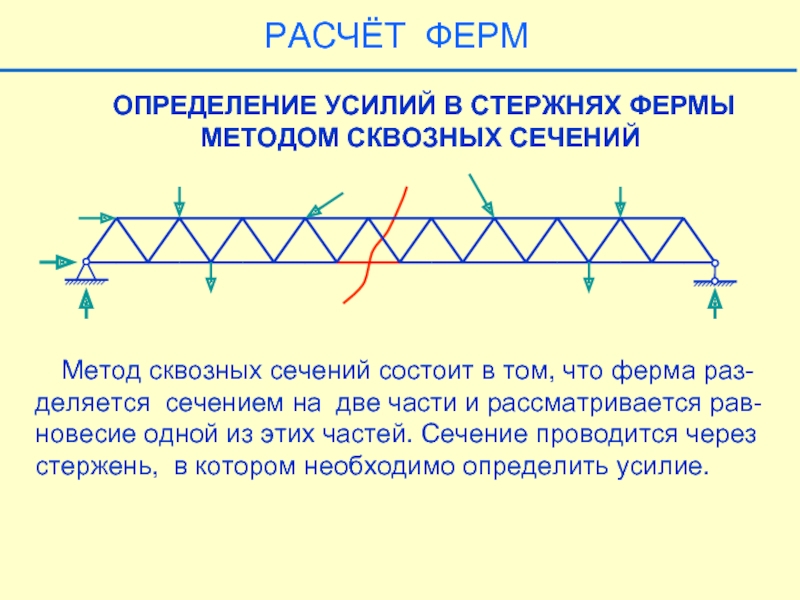
Слайд 29 ОПРЕДЕЛЕНИЕ УСИЛИЙ В СТЕРЖНЯХ ФЕРМЫ
МЕТОДОМ СКВОЗНЫХ СЕЧЕНИЙ
Метод сквозных
сечений состоит в том, что ферма раз-
деляется сечением на две части и рассматривается рав-
новесие одной из этих частей. Сечение проводится через
стержень, в котором необходимо определить усилие.
деляется сечением на две части и рассматривается рав-
новесие одной из этих частей. Сечение проводится через
стержень, в котором необходимо определить усилие.
РАСЧЁТ ФЕРМ
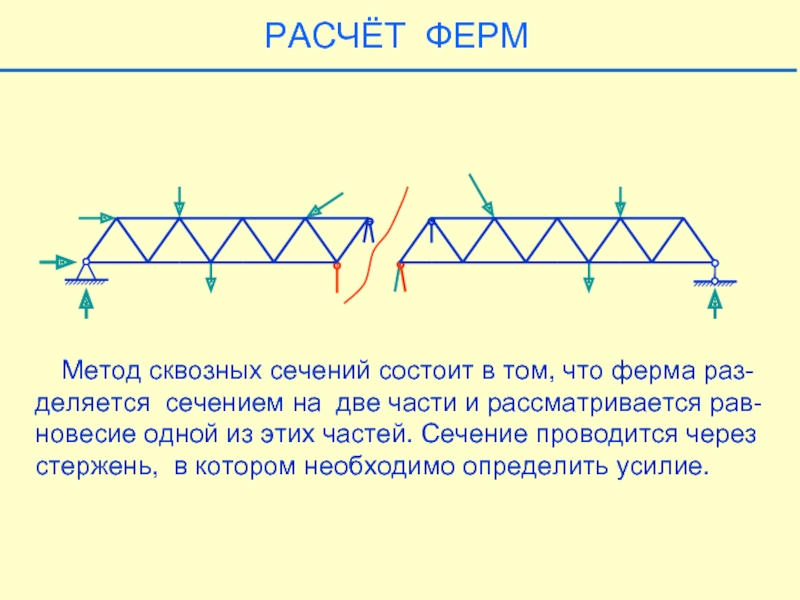
Слайд 30 Метод сквозных сечений состоит в том, что ферма раз-
деляется
сечением на две части и рассматривается рав-
новесие одной из этих частей. Сечение проводится через
стержень, в котором необходимо определить усилие.
новесие одной из этих частей. Сечение проводится через
стержень, в котором необходимо определить усилие.
РАСЧЁТ ФЕРМ
Слайд 31
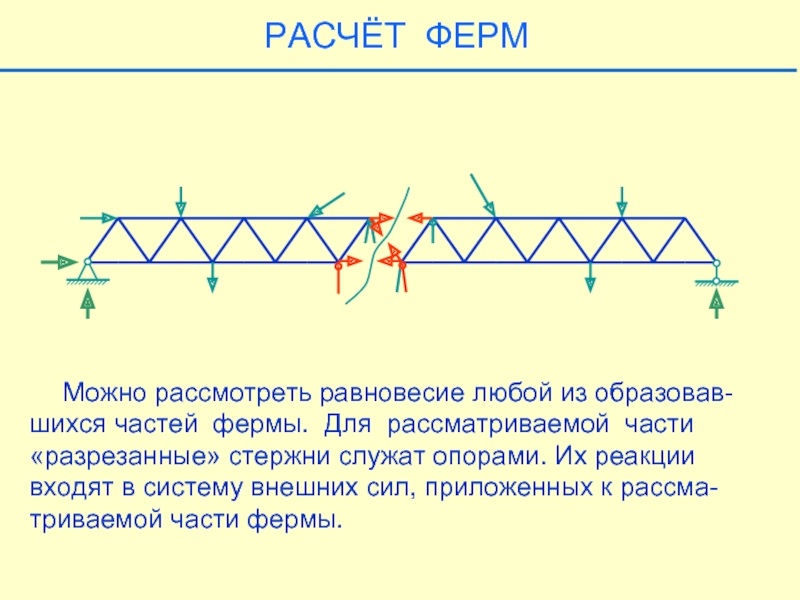
Можно рассмотреть равновесие любой из образовав-шихся частей фермы.
Для рассматриваемой части «разрезанные» стержни служат опорами. Их реакции входят в систему внешних сил, приложенных к рассма-триваемой части фермы.
РАСЧЁТ ФЕРМ
Слайд 32
РАСЧЁТ ФЕРМ
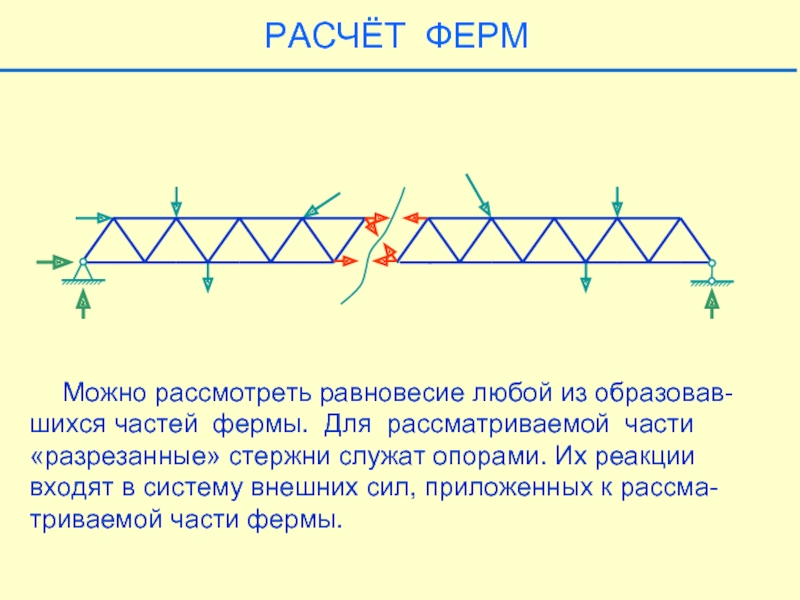
Можно рассмотреть равновесие любой из образовав-шихся частей
фермы. Для рассматриваемой части «разрезанные» стержни служат опорами. Их реакции входят в систему внешних сил, приложенных к рассма-триваемой части фермы.
Слайд 33
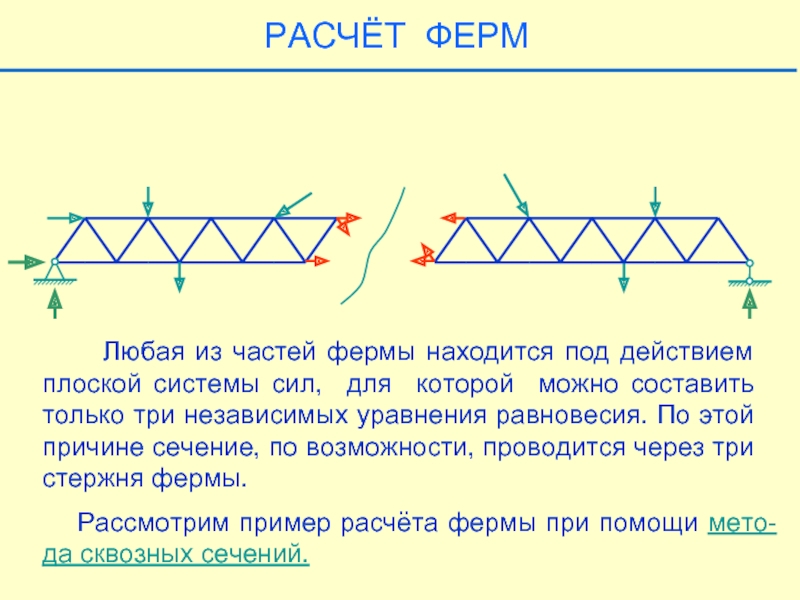
РАСЧЁТ ФЕРМ
Любая из частей фермы находится под действием
плоской системы сил, для которой можно составить только три независимых уравнения равновесия. По этой причине сечение, по возможности, проводится через три стержня фермы.
Рассмотрим пример расчёта фермы при помощи мето-да сквозных сечений.
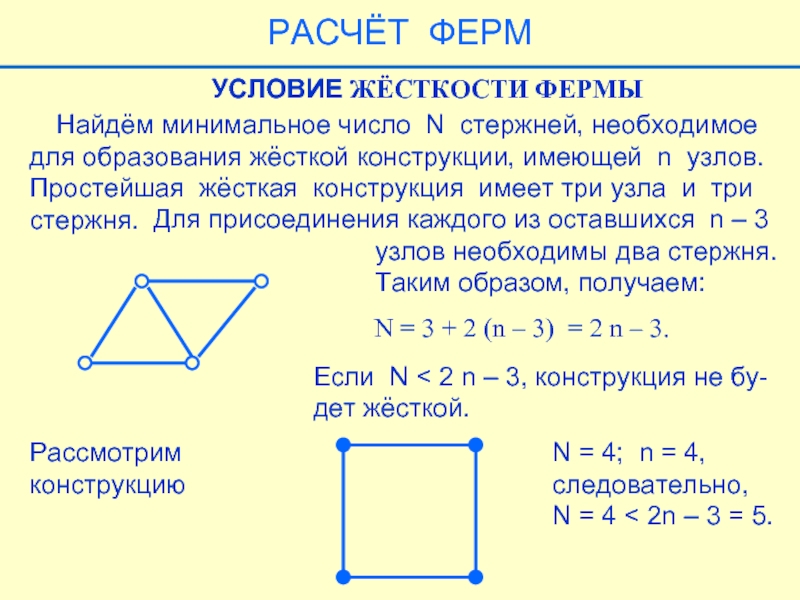
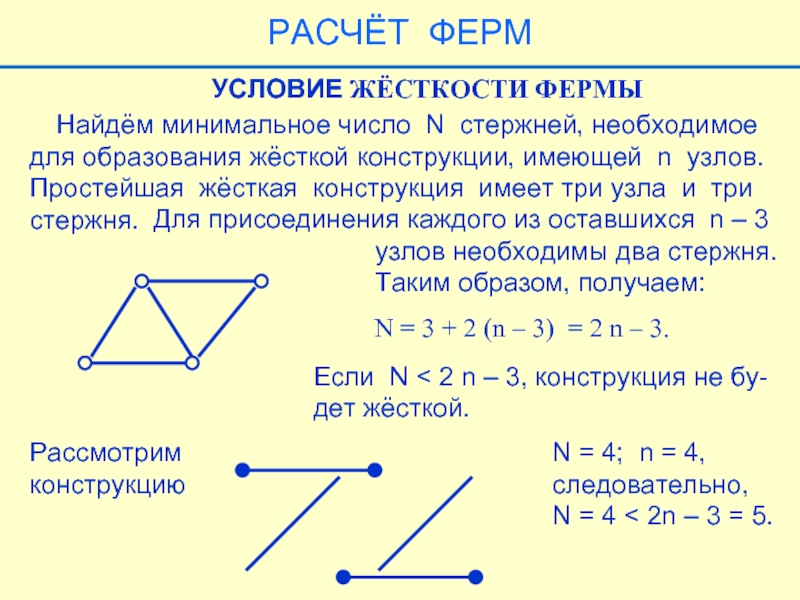
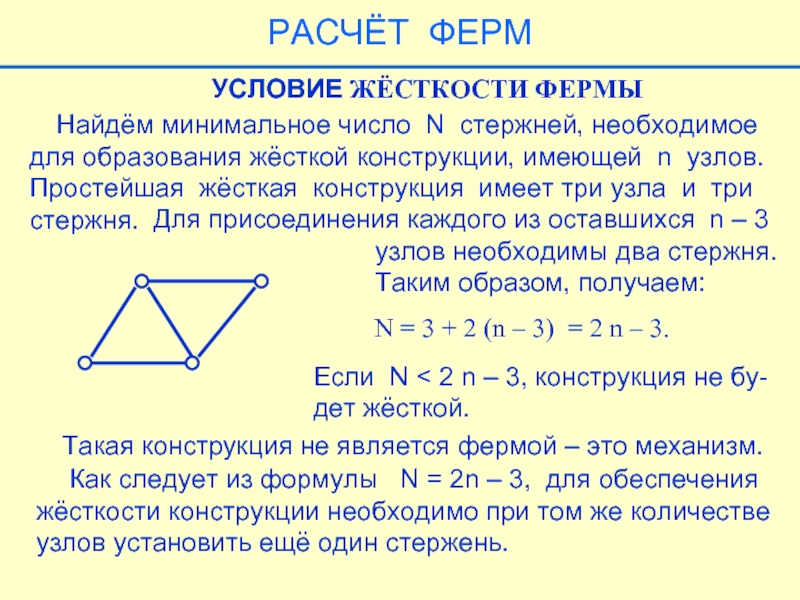
Слайд 34 Найдём минимальное число N стержней, необходимое
для образования жёсткой
конструкции, имеющей n узлов.
Простейшая жёсткая конструкция имеет три узла и три
стержня.
Простейшая жёсткая конструкция имеет три узла и три
стержня.
Для присоединения каждого из оставшихся n – 3
узлов необходимы два стержня.
Таким образом, получаем:
УСЛОВИЕ ЖЁСТКОСТИ ФЕРМЫ
N = 3 + 2 (n – 3) = 2 n – 3.
Если N < 2 n – 3, конструкция не бу-
дет жёсткой.
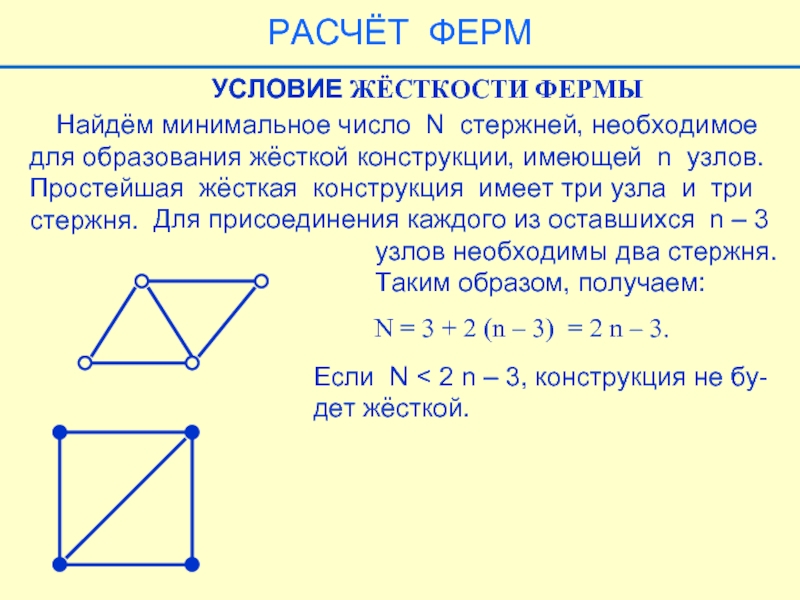
Рассмотрим
конструкцию
N = 4; n = 4,
следовательно,
N = 4 < 2n – 3 = 5.
РАСЧЁТ ФЕРМ
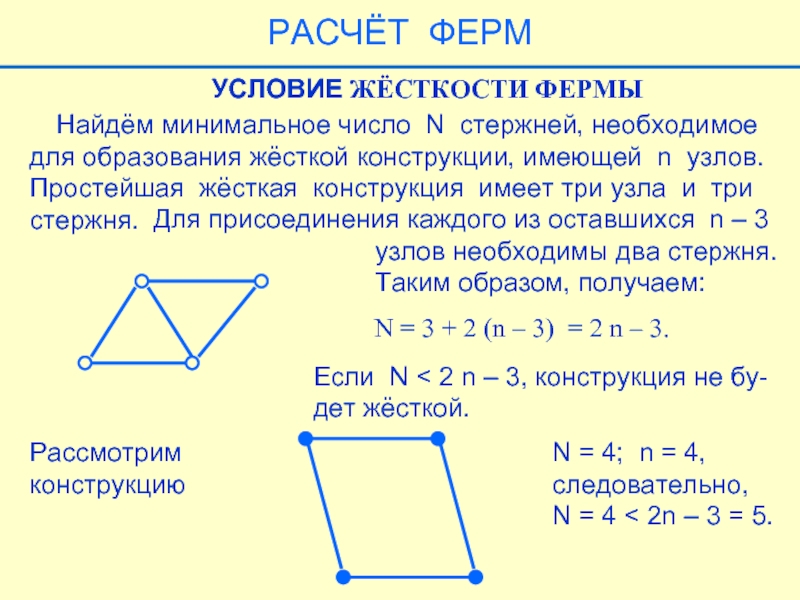
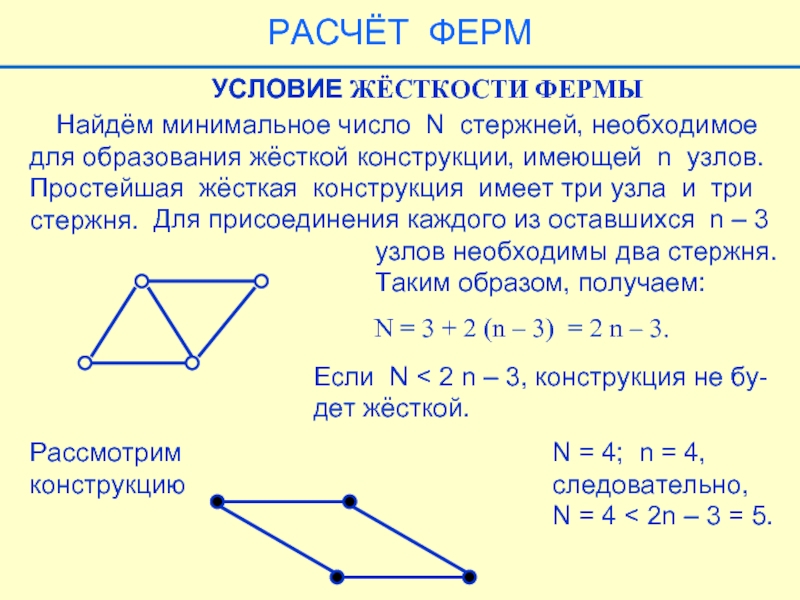
Слайд 35 Найдём минимальное число N стержней, необходимое
для образования жёсткой
конструкции, имеющей n узлов.
Простейшая жёсткая конструкция имеет три узла и три
стержня.
Простейшая жёсткая конструкция имеет три узла и три
стержня.
Для присоединения каждого из оставшихся n – 3
узлов необходимы два стержня.
Таким образом, получаем:
УСЛОВИЕ ЖЁСТКОСТИ ФЕРМЫ
N = 3 + 2 (n – 3) = 2 n – 3.
Если N < 2 n – 3, конструкция не бу-
дет жёсткой.
Рассмотрим
конструкцию
N = 4; n = 4,
следовательно,
N = 4 < 2n – 3 = 5.
РАСЧЁТ ФЕРМ
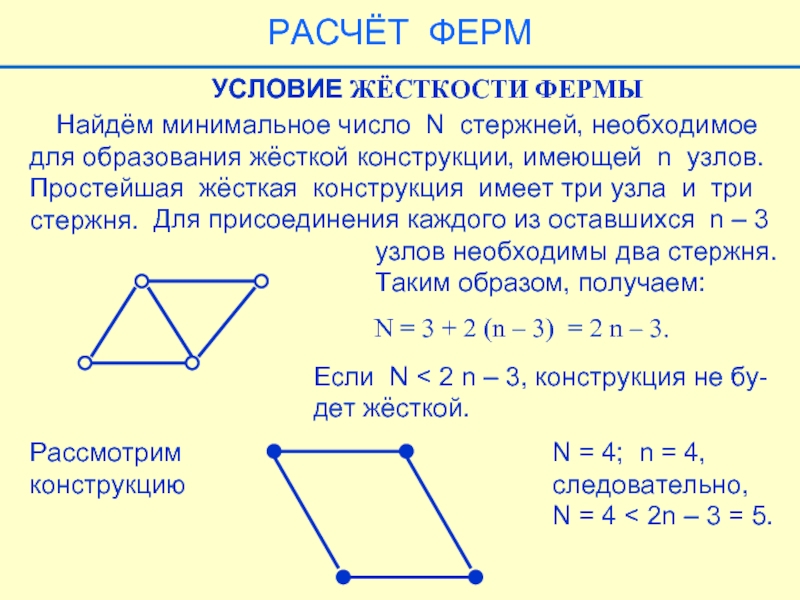
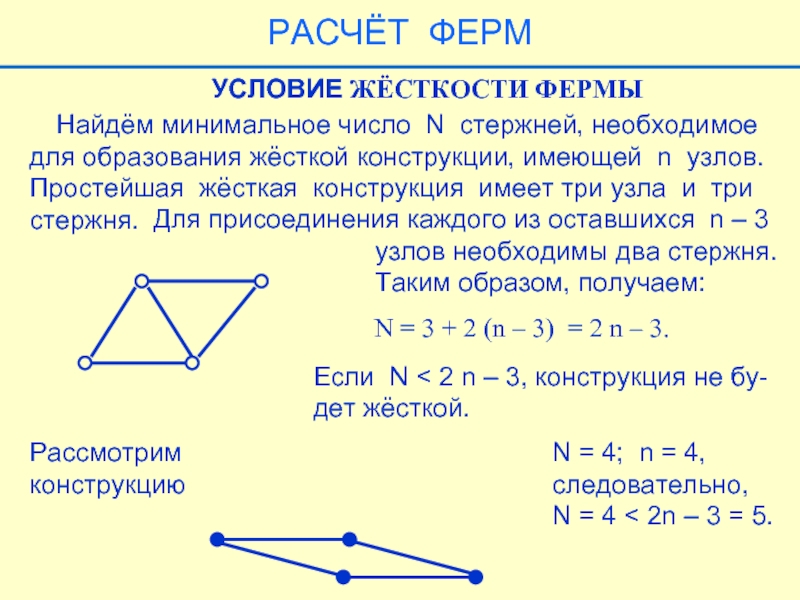
Слайд 36 Найдём минимальное число N стержней, необходимое
для образования жёсткой
конструкции, имеющей n узлов.
Простейшая жёсткая конструкция имеет три узла и три
стержня.
Простейшая жёсткая конструкция имеет три узла и три
стержня.
Для присоединения каждого из оставшихся n – 3
узлов необходимы два стержня.
Таким образом, получаем:
УСЛОВИЕ ЖЁСТКОСТИ ФЕРМЫ
N = 3 + 2 (n – 3) = 2 n – 3.
Если N < 2 n – 3, конструкция не бу-
дет жёсткой.
Рассмотрим
конструкцию
N = 4; n = 4,
следовательно,
N = 4 < 2n – 3 = 5.
РАСЧЁТ ФЕРМ
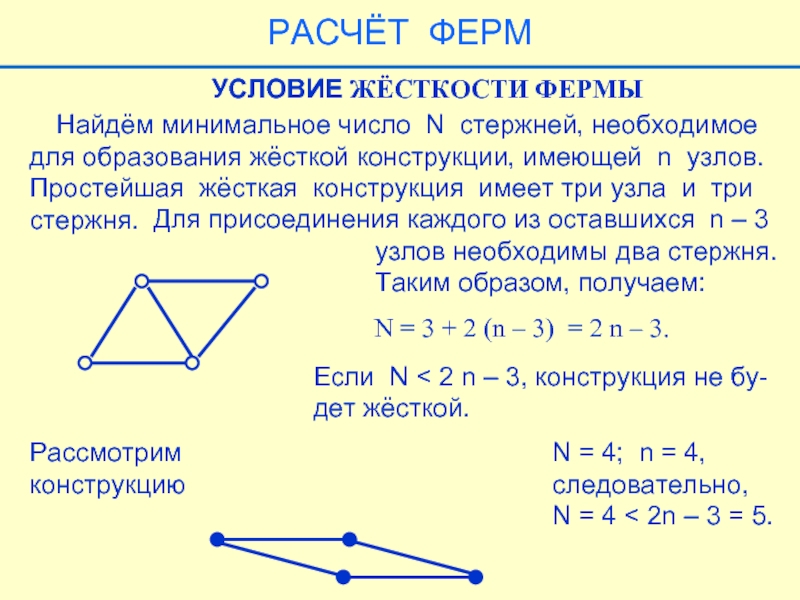
Слайд 37 Найдём минимальное число N стержней, необходимое
для образования жёсткой
конструкции, имеющей n узлов.
Простейшая жёсткая конструкция имеет три узла и три
стержня.
Простейшая жёсткая конструкция имеет три узла и три
стержня.
Для присоединения каждого из оставшихся n – 3
узлов необходимы два стержня.
Таким образом, получаем:
УСЛОВИЕ ЖЁСТКОСТИ ФЕРМЫ
N = 3 + 2 (n – 3) = 2 n – 3.
Если N < 2 n – 3, конструкция не бу-
дет жёсткой.
Рассмотрим
конструкцию
N = 4; n = 4,
следовательно,
N = 4 < 2n – 3 = 5.
РАСЧЁТ ФЕРМ
Слайд 38 Найдём минимальное число N стержней, необходимое
для образования жёсткой
конструкции, имеющей n узлов.
Простейшая жёсткая конструкция имеет три узла и три
стержня.
Простейшая жёсткая конструкция имеет три узла и три
стержня.
Для присоединения каждого из оставшихся n – 3
узлов необходимы два стержня.
Таким образом, получаем:
УСЛОВИЕ ЖЁСТКОСТИ ФЕРМЫ
N = 3 + 2 (n – 3) = 2 n – 3.
Если N < 2 n – 3, конструкция не бу-
дет жёсткой.
Рассмотрим
конструкцию
N = 4; n = 4,
следовательно,
N = 4 < 2n – 3 = 5.
РАСЧЁТ ФЕРМ
Слайд 39 Найдём минимальное число N стержней, необходимое
для образования жёсткой
конструкции, имеющей n узлов.
Простейшая жёсткая конструкция имеет три узла и три
стержня.
Простейшая жёсткая конструкция имеет три узла и три
стержня.
Для присоединения каждого из оставшихся n – 3
узлов необходимы два стержня.
Таким образом, получаем:
УСЛОВИЕ ЖЁСТКОСТИ ФЕРМЫ
N = 3 + 2 (n – 3) = 2 n – 3.
Если N < 2 n – 3, конструкция не бу-
дет жёсткой.
Рассмотрим
конструкцию
N = 4; n = 4,
следовательно,
N = 4 < 2n – 3 = 5.
РАСЧЁТ ФЕРМ
Слайд 40 Найдём минимальное число N стержней, необходимое
для образования жёсткой
конструкции, имеющей n узлов.
Простейшая жёсткая конструкция имеет три узла и три
стержня.
Простейшая жёсткая конструкция имеет три узла и три
стержня.
Для присоединения каждого из оставшихся n – 3
узлов необходимы два стержня.
Таким образом, получаем:
УСЛОВИЕ ЖЁСТКОСТИ ФЕРМЫ
N = 3 + 2 (n – 3) = 2 n – 3.
Если N < 2 n – 3, конструкция не бу-
дет жёсткой.
Рассмотрим
конструкцию
N = 4; n = 4,
следовательно,
N = 4 < 2n – 3 = 5.
РАСЧЁТ ФЕРМ
Слайд 41 Найдём минимальное число N стержней, необходимое
для образования жёсткой
конструкции, имеющей n узлов.
Простейшая жёсткая конструкция имеет три узла и три
стержня.
Простейшая жёсткая конструкция имеет три узла и три
стержня.
Для присоединения каждого из оставшихся n – 3
узлов необходимы два стержня.
Таким образом, получаем:
УСЛОВИЕ ЖЁСТКОСТИ ФЕРМЫ
N = 3 + 2 (n – 3) = 2 n – 3.
Если N < 2 n – 3, конструкция не бу-
дет жёсткой.
РАСЧЁТ ФЕРМ
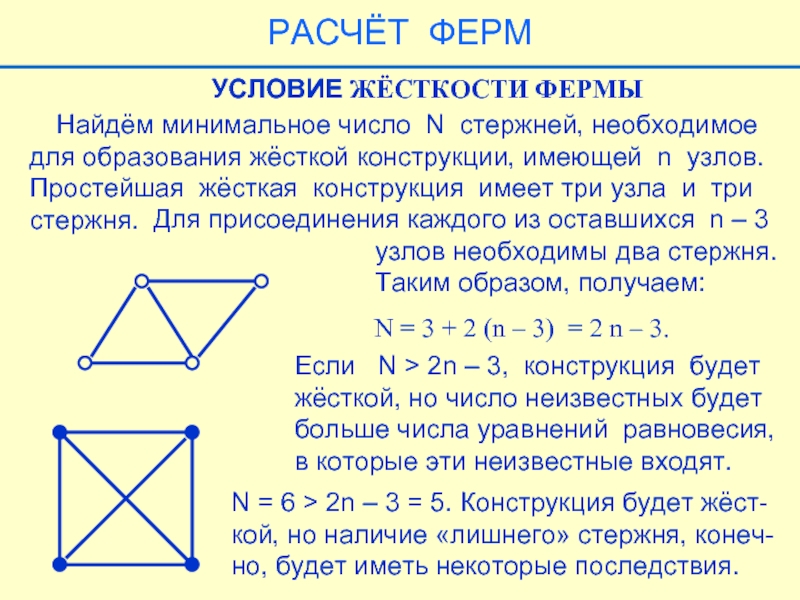
Такая конструкция не является фермой – это механизм.
Как следует из формулы N = 2n – 3, для обеспечения
жёсткости конструкции необходимо при том же количестве узлов установить ещё один стержень.
Слайд 42 Найдём минимальное число N стержней, необходимое
для образования жёсткой
конструкции, имеющей n узлов.
Простейшая жёсткая конструкция имеет три узла и три
стержня.
Простейшая жёсткая конструкция имеет три узла и три
стержня.
Для присоединения каждого из оставшихся n – 3
узлов необходимы два стержня.
Таким образом, получаем:
УСЛОВИЕ ЖЁСТКОСТИ ФЕРМЫ
N = 3 + 2 (n – 3) = 2 n – 3.
Если N < 2 n – 3, конструкция не бу-
дет жёсткой.
РАСЧЁТ ФЕРМ
Слайд 43 Найдём минимальное число N стержней, необходимое
для образования жёсткой
конструкции, имеющей n узлов.
Простейшая жёсткая конструкция имеет три узла и три
стержня.
Простейшая жёсткая конструкция имеет три узла и три
стержня.
Для присоединения каждого из оставшихся n – 3
узлов необходимы два стержня.
Таким образом, получаем:
УСЛОВИЕ ЖЁСТКОСТИ ФЕРМЫ
N = 3 + 2 (n – 3) = 2 n – 3.
РАСЧЁТ ФЕРМ
Если N > 2n – 3, конструкция будет
жёсткой, но число неизвестных будет
больше числа уравнений равновесия,
в которые эти неизвестные входят.
N = 6 > 2n – 3 = 5. Конструкция будет жёст-кой, но наличие «лишнего» стержня, конеч-но, будет иметь некоторые последствия.
Слайд 44 УСЛОВИЕ СТАТИЧЕСКОЙ ОПРЕДЕЛИМОСТИ ФЕРМЫ
Ферма называется статически определимой,
если чис-
ло неизвестных равно числу уравнений равновесия, в ко-
торые эти неизвестные входят. Для фермы, имеющей n
узлов, можно составить 2n независимых уравнений рав-
новесия. В число неизвестных входят N усилий в стерж-
нях фермы и три составляющие реакций внешних опор. Таким образом, ферма будет статически определимой
при выолнении условия
N = 2n – 3,
которое, как видно, совпадает с условием жёсткости.
ло неизвестных равно числу уравнений равновесия, в ко-
торые эти неизвестные входят. Для фермы, имеющей n
узлов, можно составить 2n независимых уравнений рав-
новесия. В число неизвестных входят N усилий в стерж-
нях фермы и три составляющие реакций внешних опор. Таким образом, ферма будет статически определимой
при выолнении условия
N = 2n – 3,
которое, как видно, совпадает с условием жёсткости.
РАСЧЁТ ФЕРМ
Слайд 45 «Лишние» опоры – ненужные для обеспечения равновесия
абсолютно твёрдого тела – могут появиться по двум основным причинам.
Во-первых, причины могут быть технологическими: перекрытие кладётся на две стены, хотя теоретически можно было бы обойтись одной заделкой.
Во-вторых, дополнительные опоры приходится устанавливать, чтобы предотвратить недопустимо большие деформации, опасные для прочности конструкции.
Во-первых, причины могут быть технологическими: перекрытие кладётся на две стены, хотя теоретически можно было бы обойтись одной заделкой.
Во-вторых, дополнительные опоры приходится устанавливать, чтобы предотвратить недопустимо большие деформации, опасные для прочности конструкции.
РАСЧЁТ ФЕРМ
УСЛОВИЕ СТАТИЧЕСКОЙ ОПРЕДЕЛИМОСТИ ФЕРМЫ
