- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Расчет линии по мощности презентация
Содержание
- 1. Расчет линии по мощности
- 2. Расчет линии по мощности Линия «без потерь»
- 3. Линия «без потерь» Как следует из положений,
- 4. Построение векторной диаграммы для линии «без
- 5. I2а и I2р – активная и реактивная
- 6. Активная мощность, отдаваемая нагрузке может быть определена
- 7. Реактивная мощность, отдаваемая нагрузке может быть определена
- 8. Активная мощность начала линии может быть определена
- 9. Реактивная мощность начала линии может быть определена
- 10. Из полученных выражений следует, что Передача активной
- 11. Очевидно, что при наличии активного сопротивления проводов
- 12. Из векторной диаграммы видно, что I1р >
- 13. Однако следует помнить, что под влиянием зарядной
- 14. Поэтому ветви емкостной проводимости, определяющие в схеме
- 15. В связи со сказанным выше, в схемах
- 16. Классификация задач расчета линии по мощности нагрузки
- 17. Задача № 1 (по данным конца) Задано:
- 18. Задача № 1 (по данным конца) Принимая
- 19. Задача № 1 (по данным конца) Потери
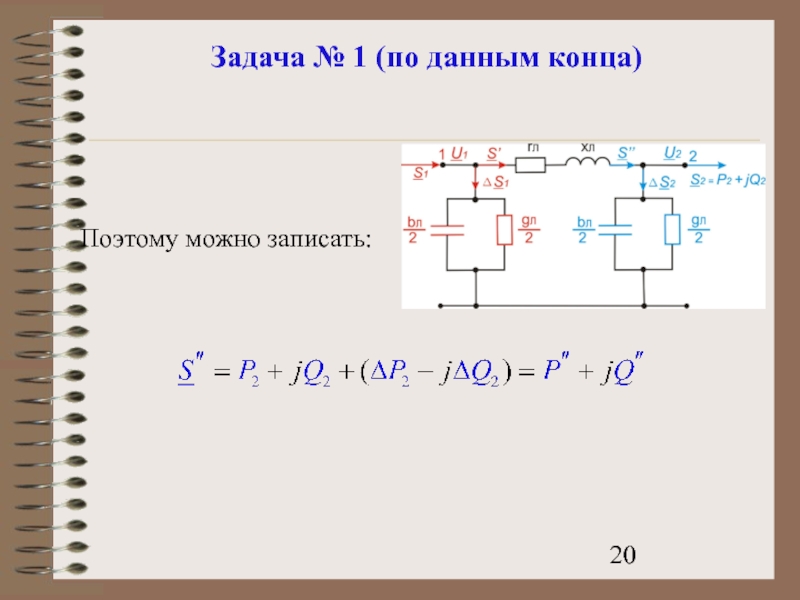
- 20. Задача № 1 (по данным конца) Поэтому можно записать:
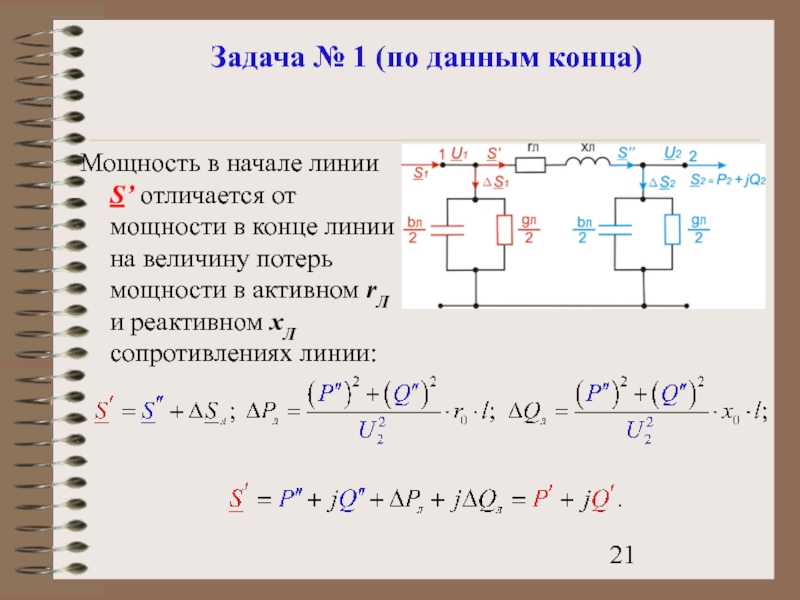
- 21. Задача № 1 (по данным конца) Мощность
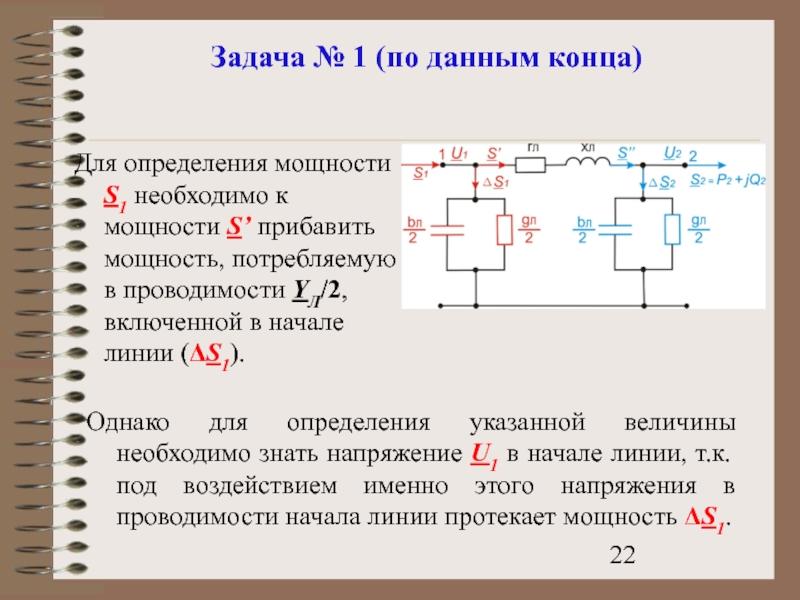
- 22. Задача № 1 (по данным конца) Для
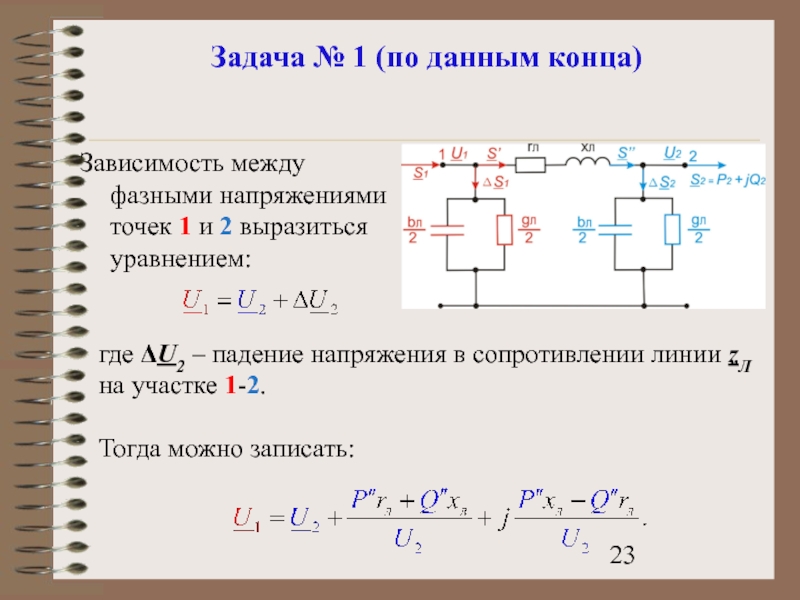
- 23. Задача № 1 (по данным конца) Зависимость
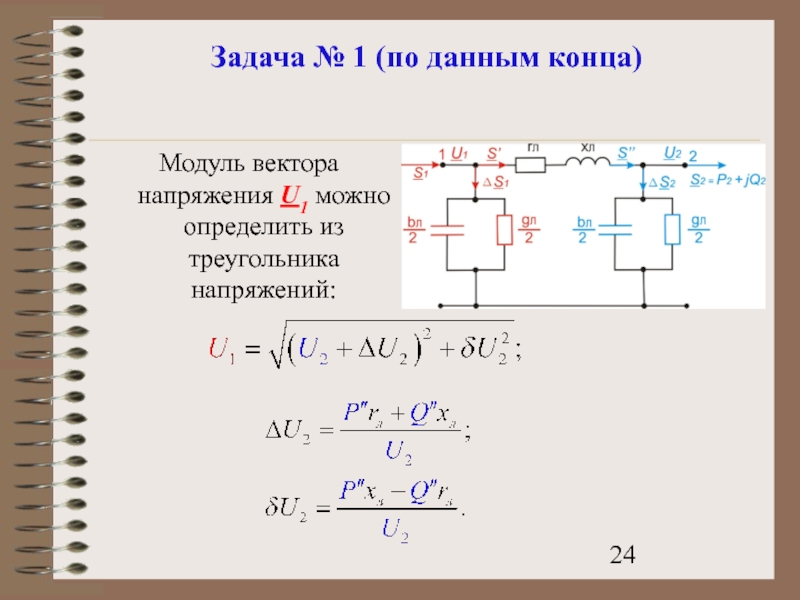
- 24. Задача № 1 (по данным конца) Модуль
- 25. Задача № 1 (по данным конца) Угол
- 26. Задача № 1 (по данным конца) Тогда
- 27. Задача № 2 (по данным начала) Задано:
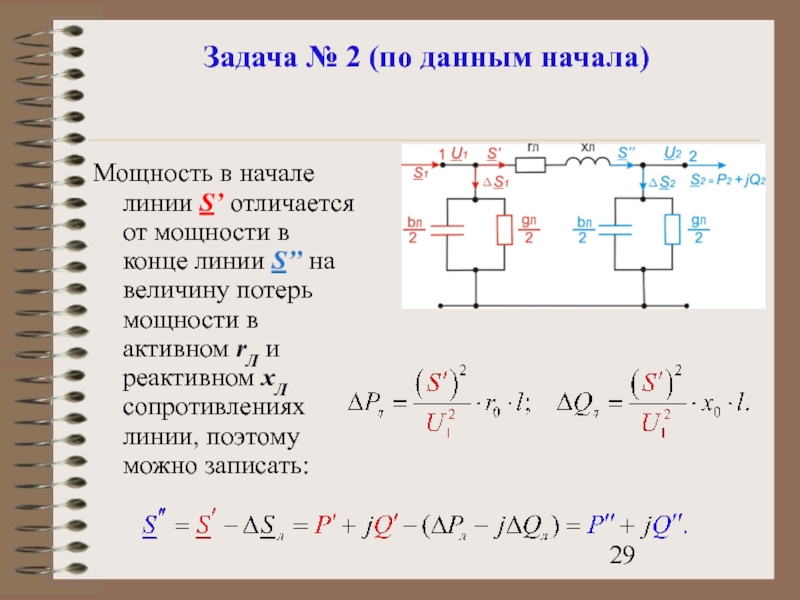
- 28. Задача № 2 (по данным начала) Мощность
- 29. Задача № 2 (по данным начала) Мощность
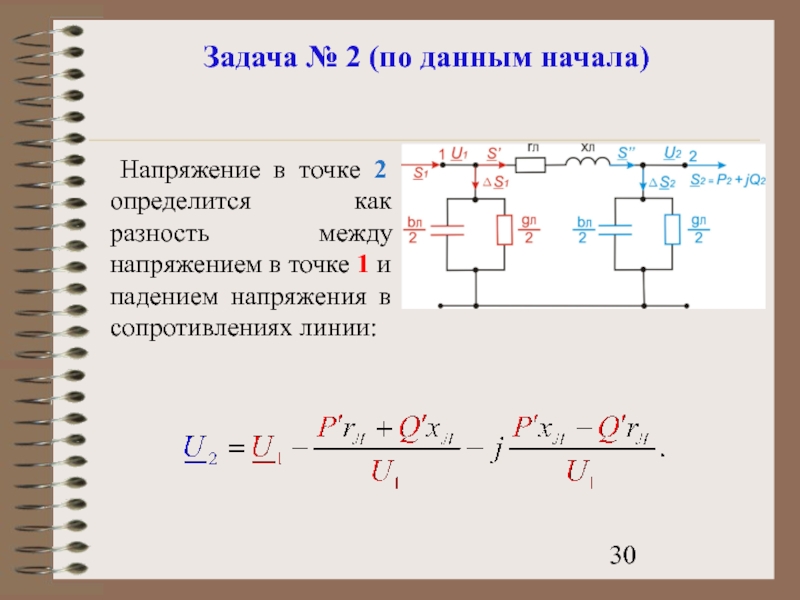
- 30. Задача № 2 (по данным начала) Напряжение
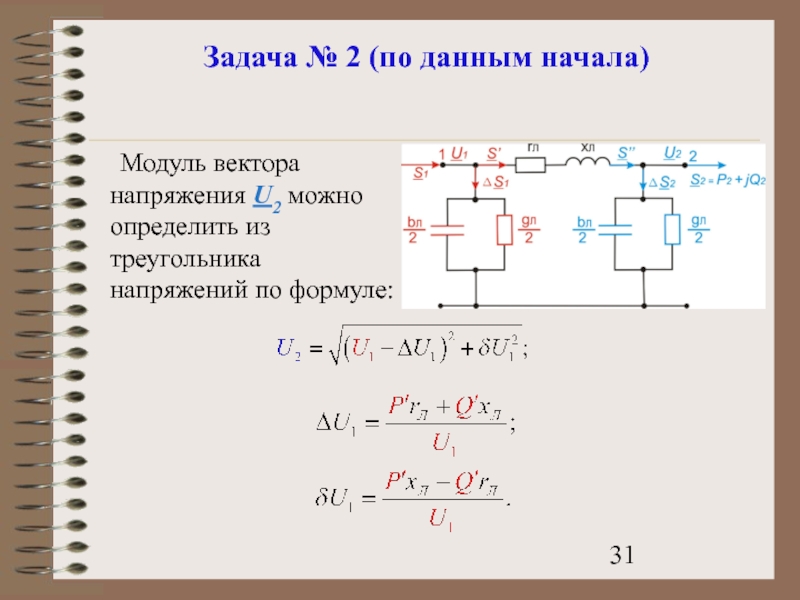
- 31. Задача № 2 (по данным начала) Модуль
- 32. Задача № 2 (по данным начала) Угол
- 33. Задача № 2 (по данным начала) По
- 34. Задача № 3 Задано: U1; S2=P2+jQ2;
- 35. Задача № 3 В данном случае расчеты
- 36. Задача № 3 (метод последовательных приближений) Каждое
- 37. Задача № 3 (метод последовательных приближений) Каждое
- 38. Задача № 3 (метод последовательных приближений) Так
- 39. Задача № 3 (метод последовательных приближений) По
- 40. Задача № 3 (метод последовательных приближений) На
- 41. Задача № 3 (метод последовательных приближений) Угол
- 42. Задача № 3 (метод последовательных приближений) Для
- 43. Понятие расчетных нагрузок подстанций (узлов). Для проведения
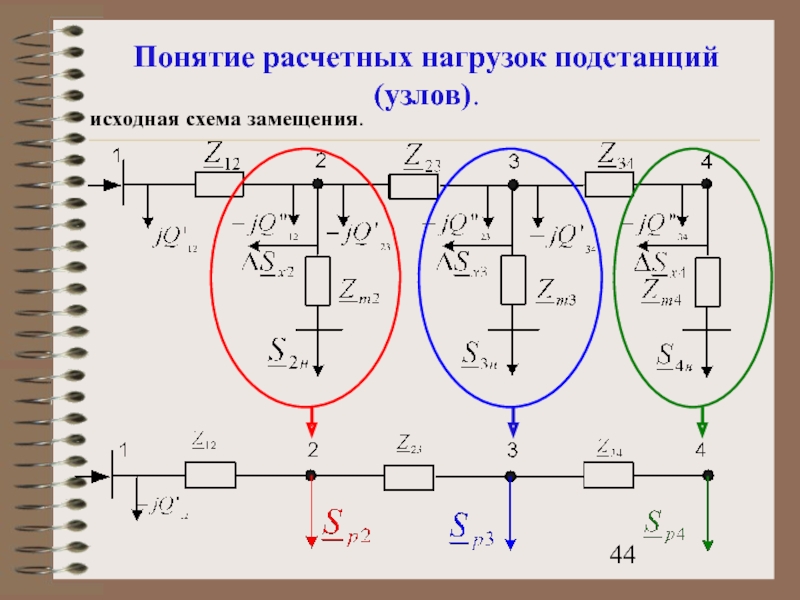
- 44. Понятие расчетных нагрузок подстанций (узлов). исходная схема замещения.
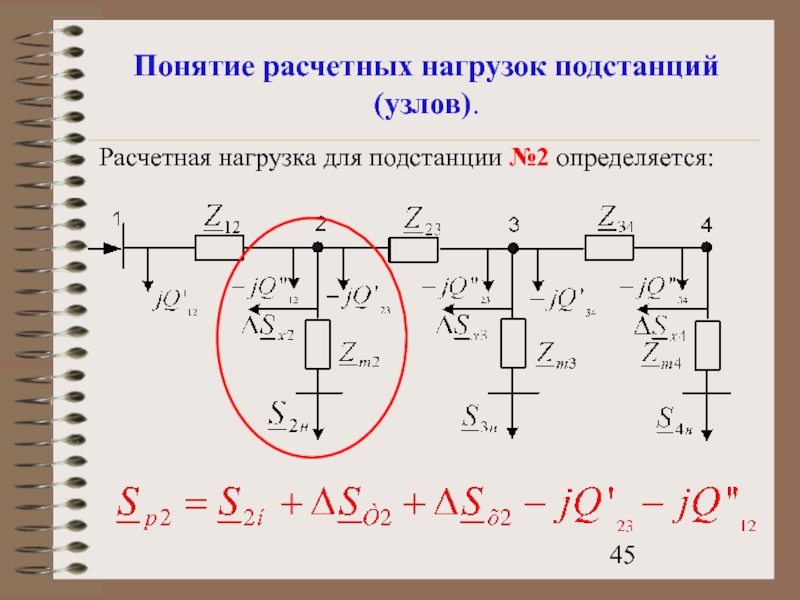
- 45. Понятие расчетных нагрузок подстанций (узлов). Расчетная нагрузка для подстанции №2 определяется:
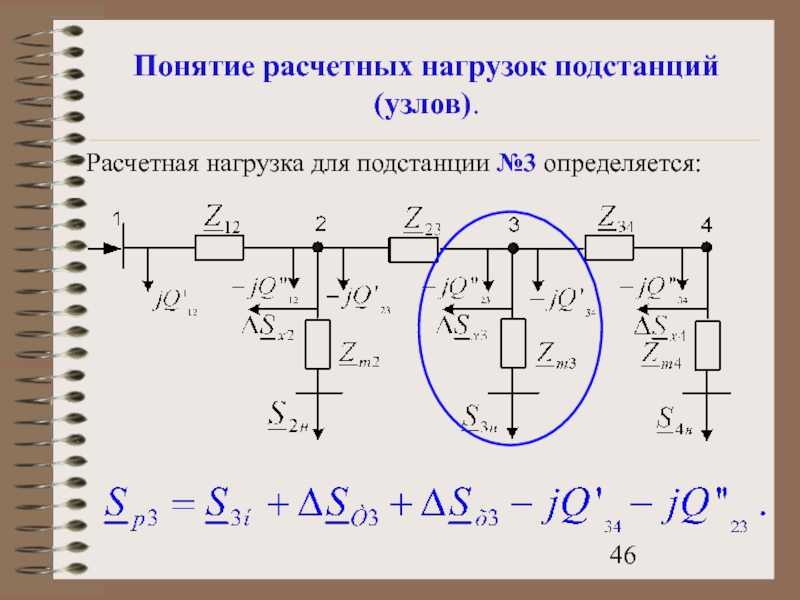
- 46. Понятие расчетных нагрузок подстанций (узлов). Расчетная нагрузка для подстанции №3 определяется:
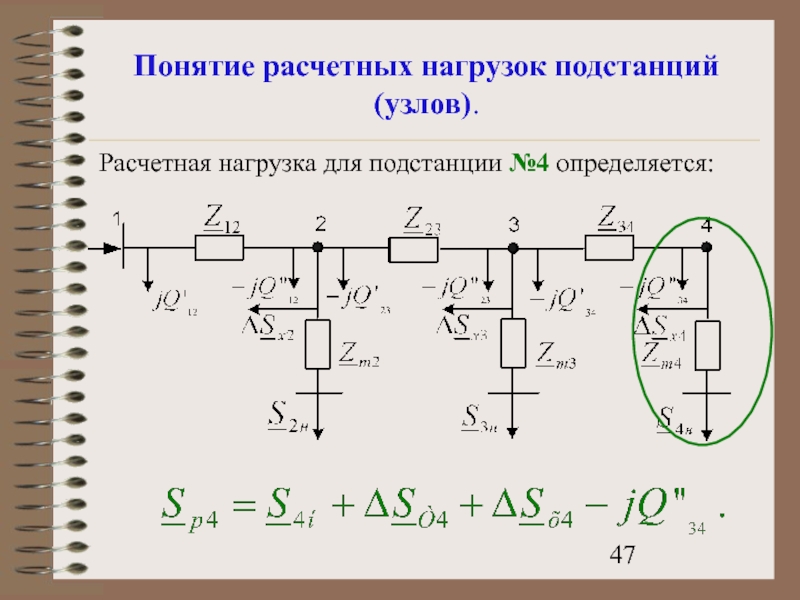
- 47. Понятие расчетных нагрузок подстанций (узлов). Расчетная нагрузка для подстанции №4 определяется:
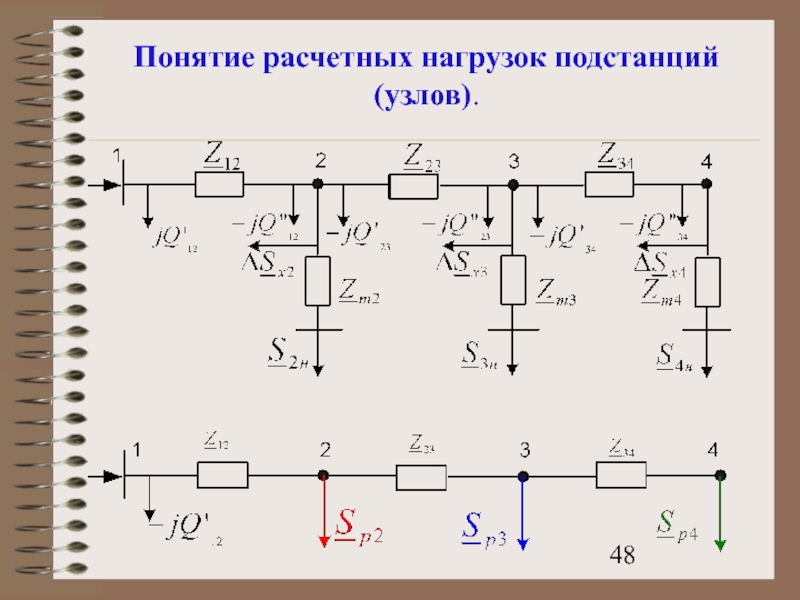
- 48. Понятие расчетных нагрузок подстанций (узлов).
- 49. Понятие расчетных нагрузок подстанций (узлов). Таким образом,
- 50. Задача № 3 (метод систематизированного подбора) Существуют
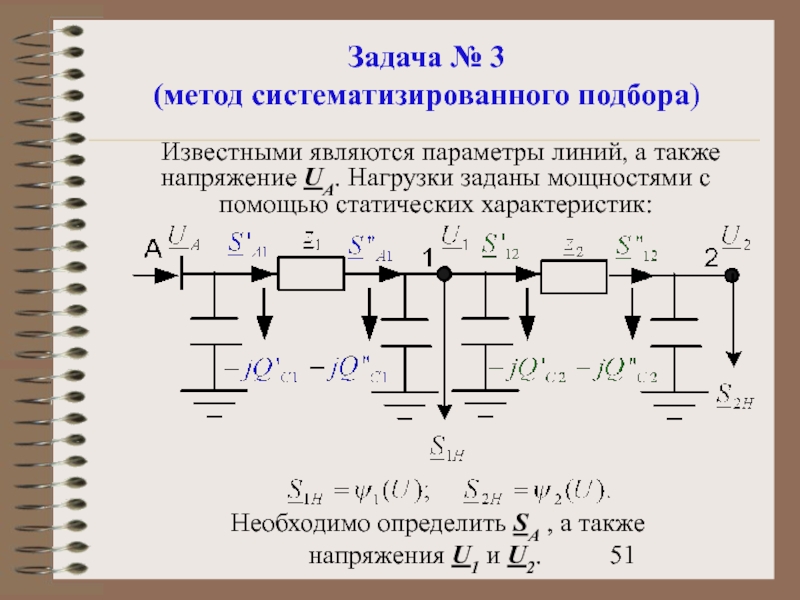
- 51. Задача № 3 (метод систематизированного подбора) Известными
- 52. Задача № 3 (метод систематизированного подбора) В
- 53. Задача № 3 (метод систематизированного подбора) Данное
- 54. Задача № 3 (метод систематизированного подбора) Суть
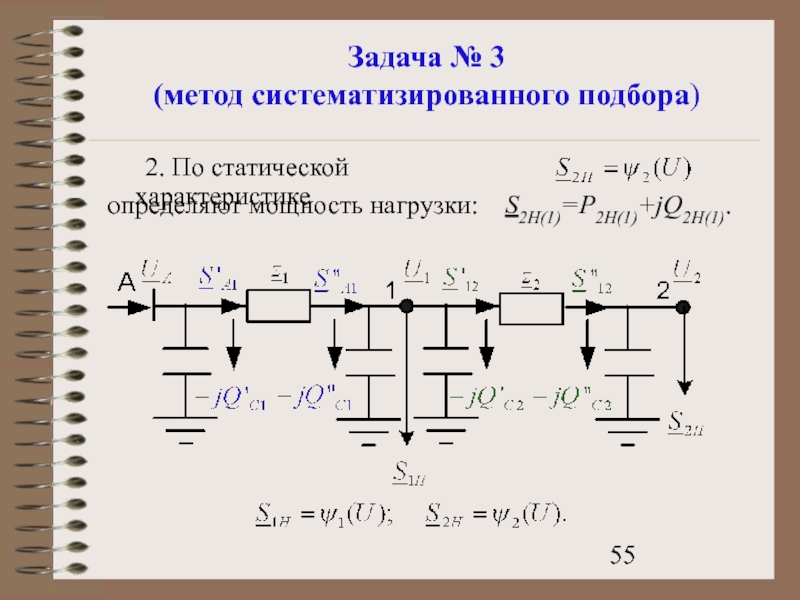
- 55. Задача № 3 (метод систематизированного подбора) 2.
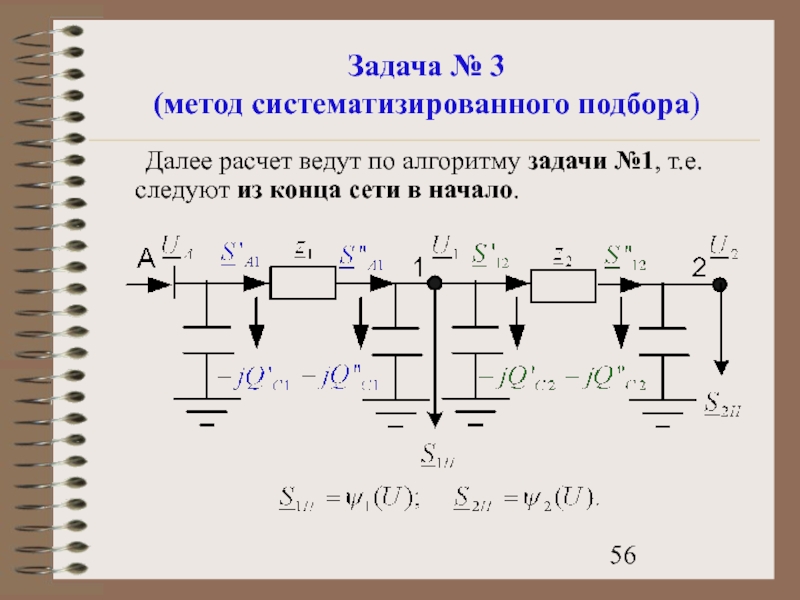
- 56. Задача № 3 (метод систематизированного подбора)
- 57. Задача № 3 (метод систематизированного подбора) 3.
- 58. Задача № 3 (метод систематизированного подбора) 4.
- 59. Задача № 3 (метод систематизированного подбора) 5.
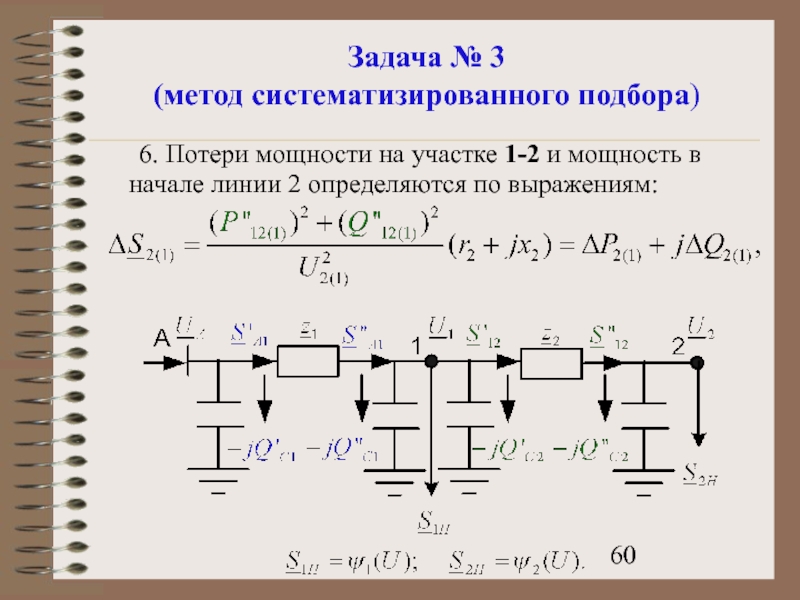
- 60. Задача № 3 (метод систематизированного подбора) 6.
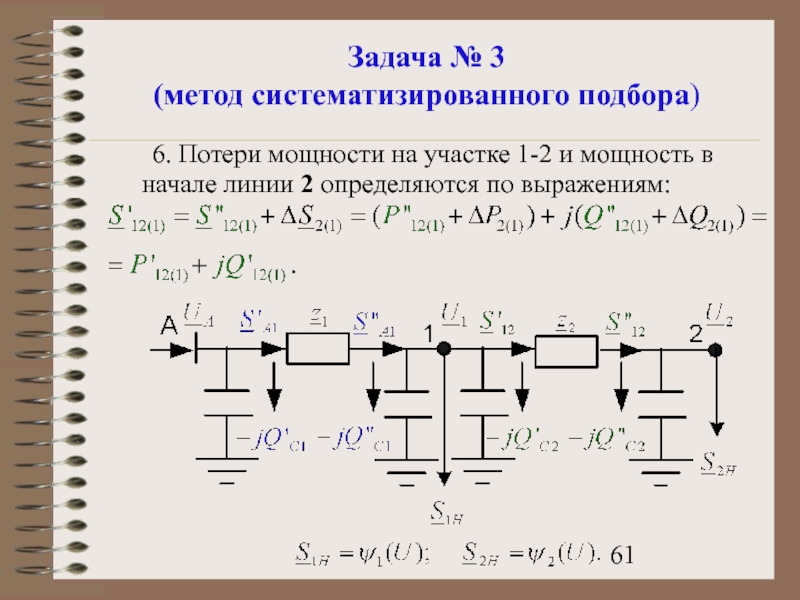
- 61. Задача № 3 (метод систематизированного подбора) 6.
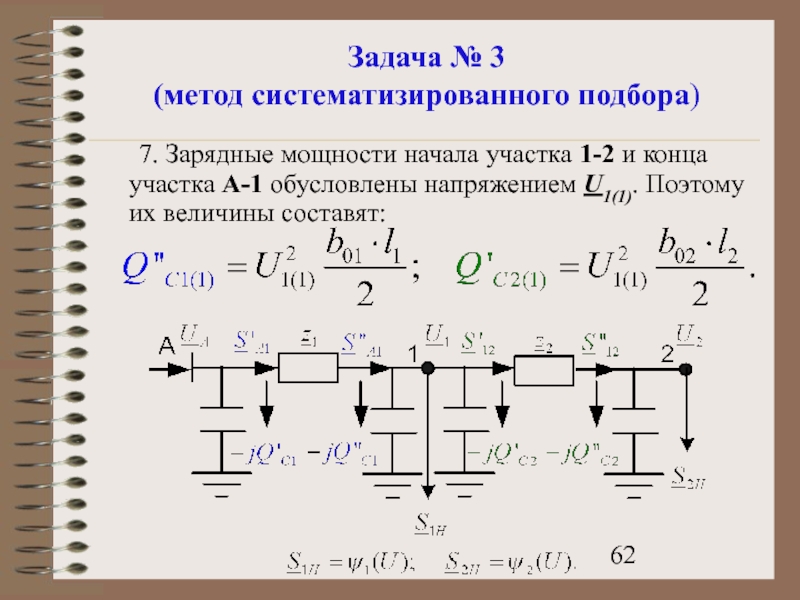
- 62. Задача № 3 (метод систематизированного подбора) 7.
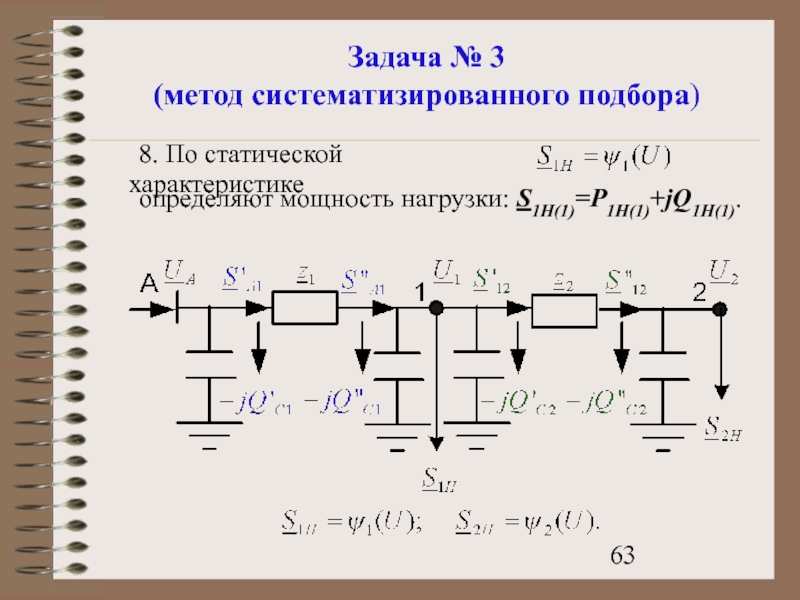
- 63. Задача № 3 (метод систематизированного подбора) 8.
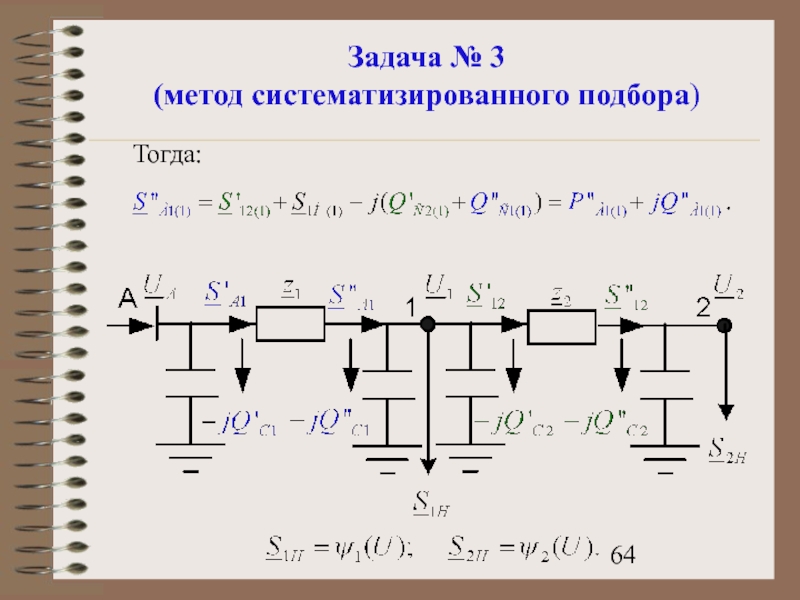
- 64. Задача № 3 (метод систематизированного подбора) Тогда:
- 65. Задача № 3 (метод систематизированного подбора) 9. Аналогичные расчеты проводят для участка А-1.
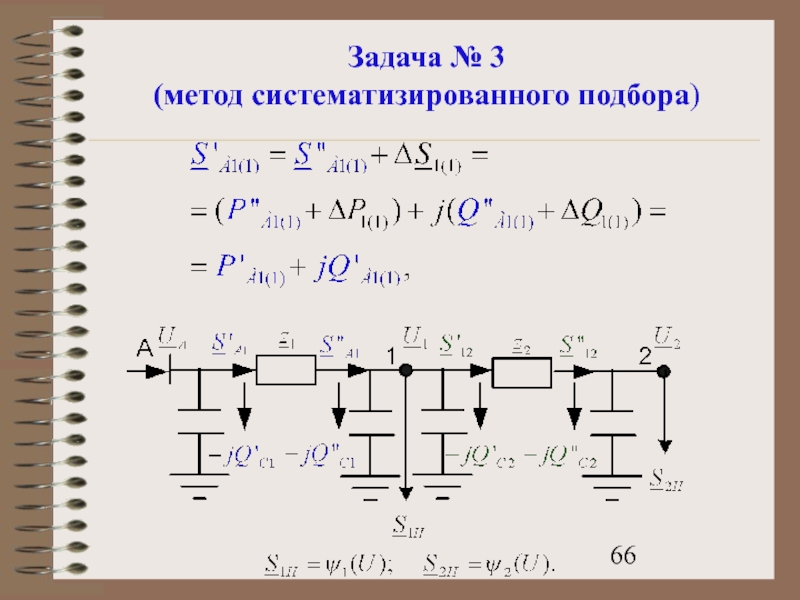
- 66. Задача № 3 (метод систематизированного подбора)
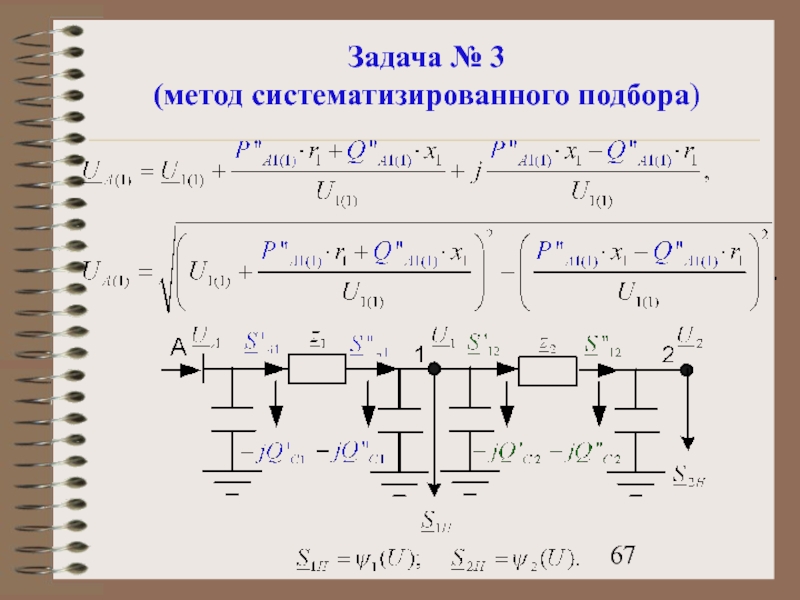
- 67. Задача № 3 (метод систематизированного подбора)
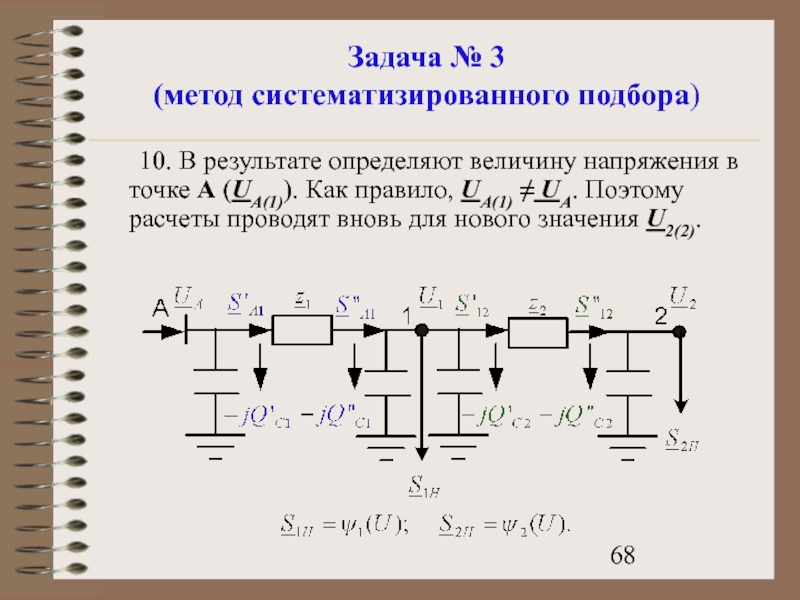
- 68. Задача № 3 (метод систематизированного подбора)
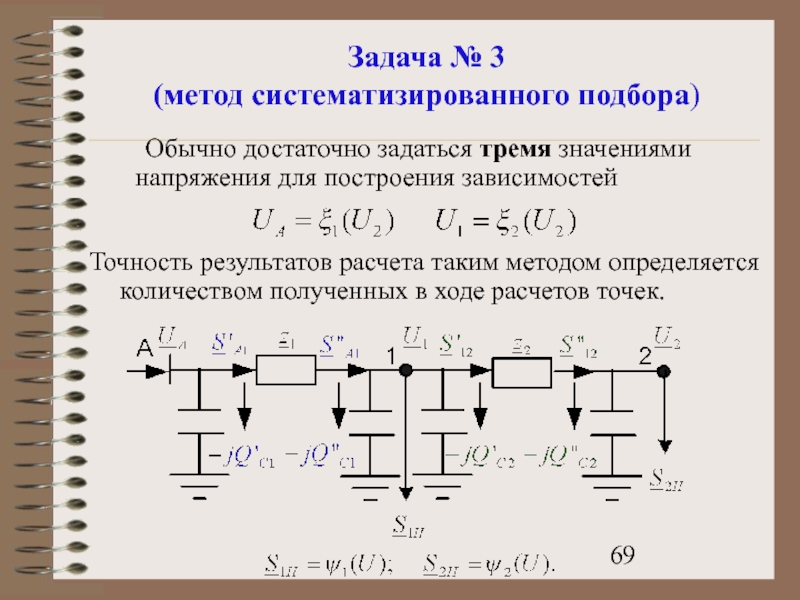
- 69. Задача № 3 (метод систематизированного подбора) Обычно
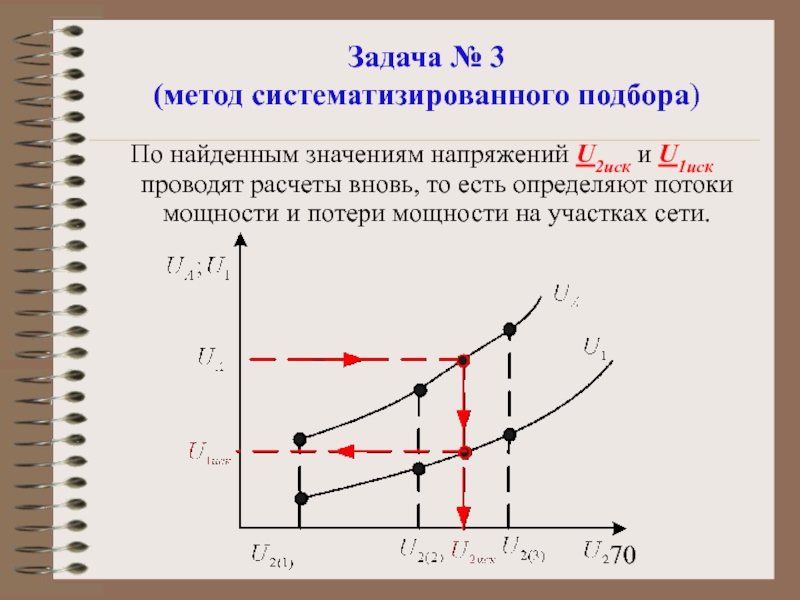
- 70. Задача № 3 (метод систематизированного подбора) По
- 71. Источники дополнительных сведений Идельчик В.И. Электрические системы
- 72. Спасибо за внимание!
Слайд 1Лекционные материалы
Дисциплина «Электроэнергетические системы и сети»
Разработаны доцентом кафедры «Электроэнергетические системы» ВятГУ
Слайд 2Расчет линии по мощности
Линия «без потерь»
Активная и реактивная мощности, передаваемые по
Классификация задач расчета линии по мощности нагрузки
Задача № 1 (по данным конца)
Задача № 2 (по данным начала)
Задача № 3 (метод последовательных приближений)
Понятие расчетных нагрузок подстанций (узлов).
Задача № 3 (метод систематизированного подбора)
Слайд 3Линия «без потерь»
Как следует из положений, приведенных ранее, потребитель, получающий питание
Для вывода зависимостей и анализа основных соотношений между параметрами линии и параметрами ее режима целесообразно рассмотреть векторную диаграмму токов и напряжений для «идеализированной» линии («линии без потерь»), т.е. для линии, у которой активное сопротивление равно нулю (r=0) и проводимости также равны нулю (y=0).
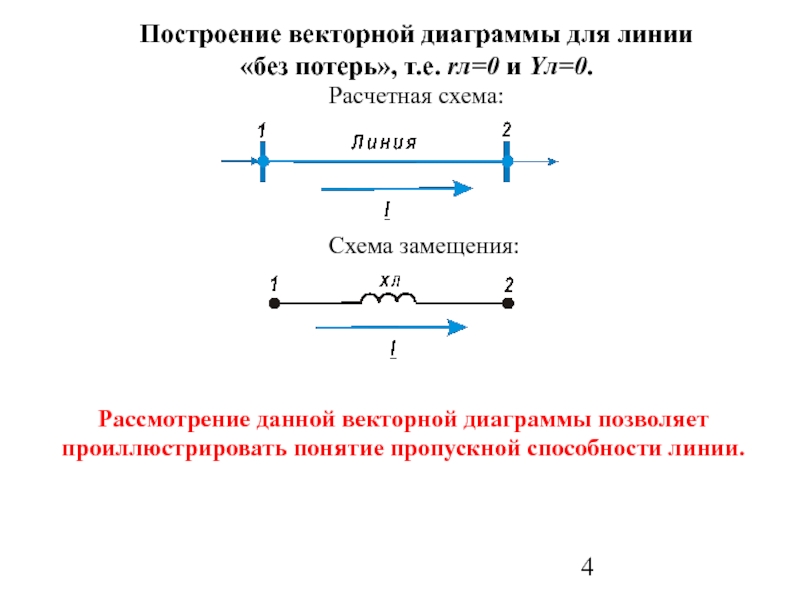
Слайд 4Построение векторной диаграммы для линии «без потерь», т.е. rл=0 и Yл=0. Расчетная
Схема замещения:
Рассмотрение данной векторной диаграммы позволяет проиллюстрировать понятие пропускной способности линии.
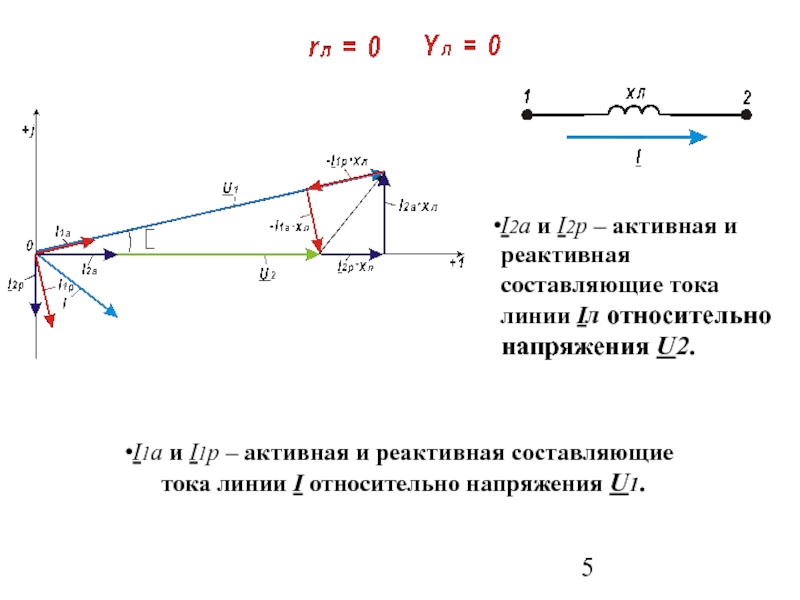
Слайд 5I2а и I2р – активная и реактивная составляющие тока линии Iл
I1а и I1р – активная и реактивная составляющие
тока линии I относительно напряжения U1.
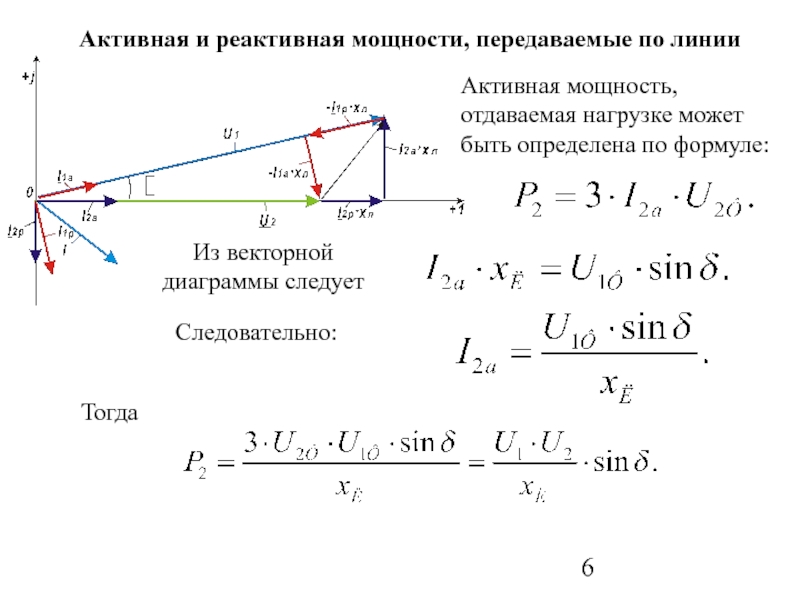
Слайд 6Активная мощность, отдаваемая нагрузке может быть определена по формуле:
Из векторной диаграммы
Активная и реактивная мощности, передаваемые по линии
Следовательно:
Тогда
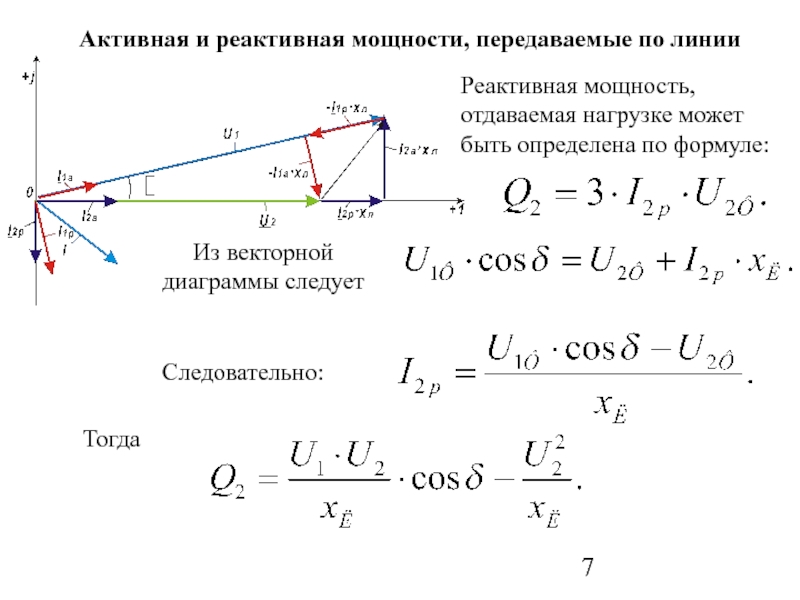
Слайд 7Реактивная мощность, отдаваемая нагрузке может быть определена по формуле:
Из векторной диаграммы
Активная и реактивная мощности, передаваемые по линии
Следовательно:
Тогда
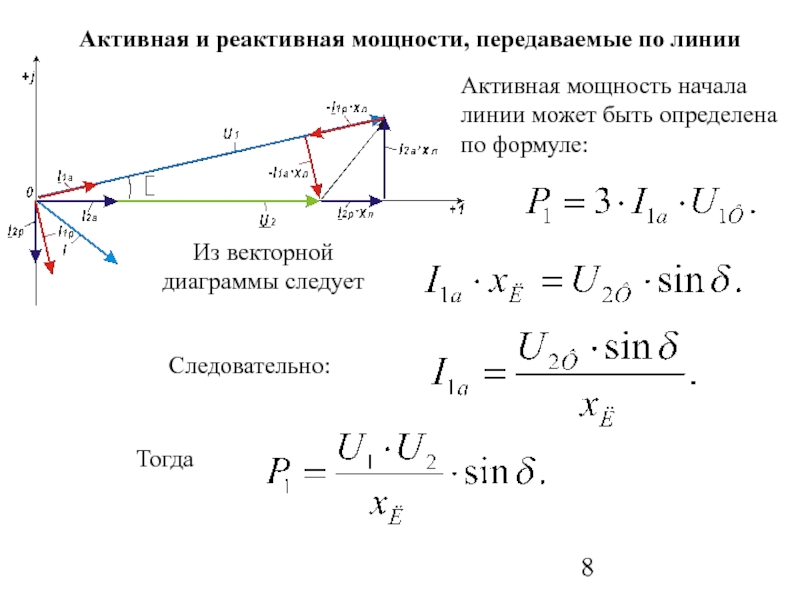
Слайд 8Активная мощность начала линии может быть определена по формуле:
Из векторной диаграммы
Активная и реактивная мощности, передаваемые по линии
Следовательно:
Тогда
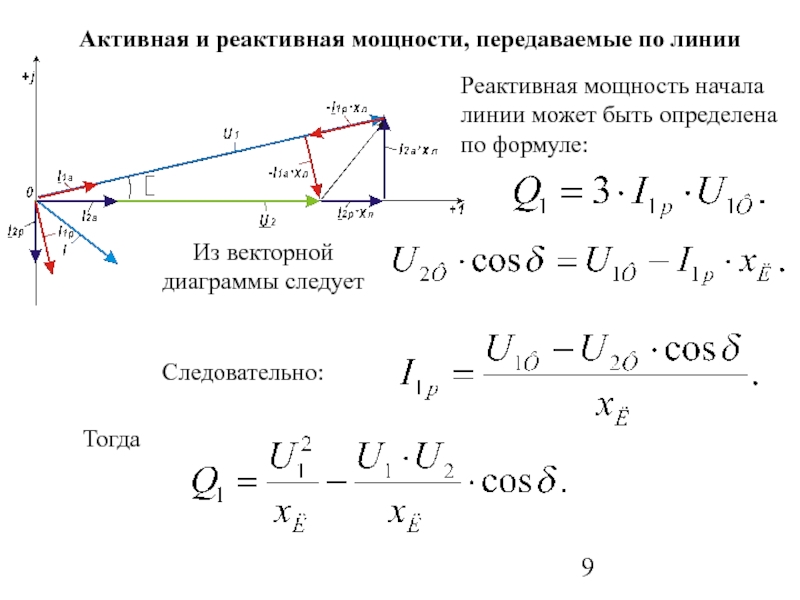
Слайд 9Реактивная мощность начала линии может быть определена по формуле:
Из векторной диаграммы
Активная и реактивная мощности, передаваемые по линии
Следовательно:
Тогда
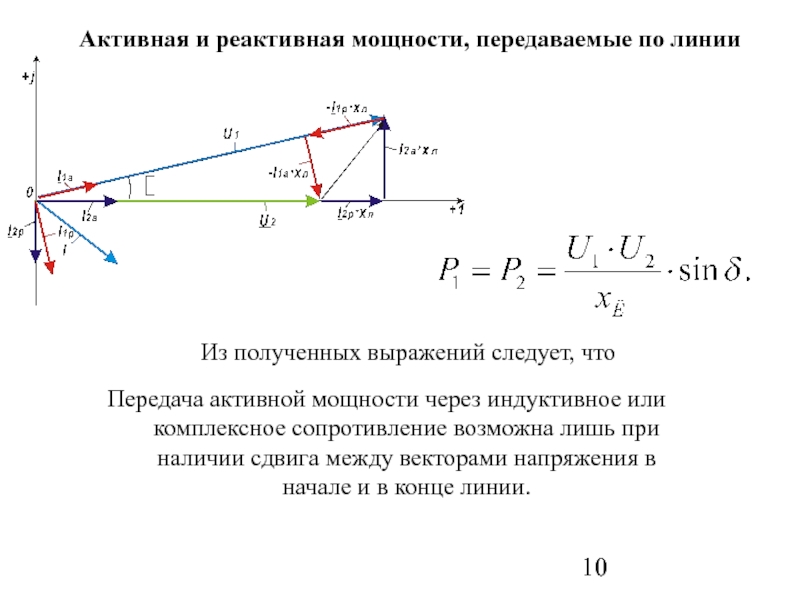
Слайд 10Из полученных выражений следует, что
Передача активной мощности через индуктивное или комплексное
Активная и реактивная мощности, передаваемые по линии
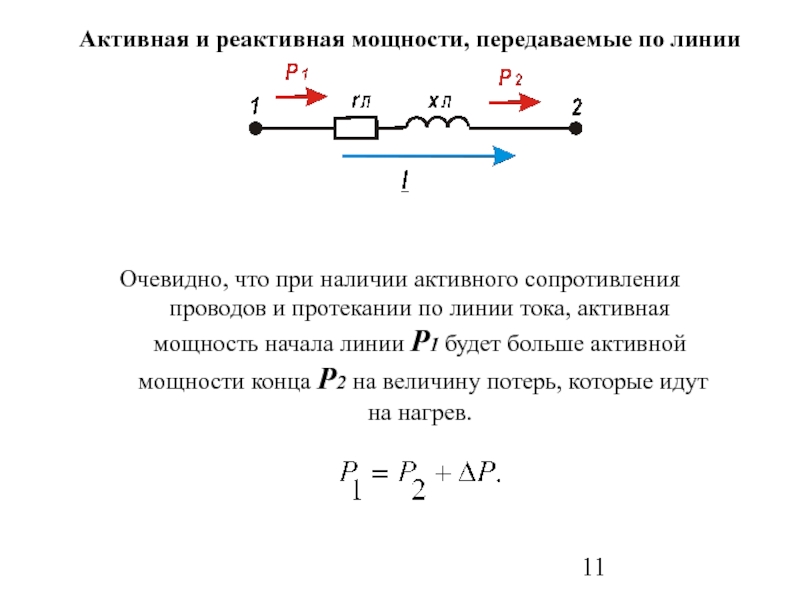
Слайд 11Очевидно, что при наличии активного сопротивления проводов и протекании по линии
Активная и реактивная мощности, передаваемые по линии
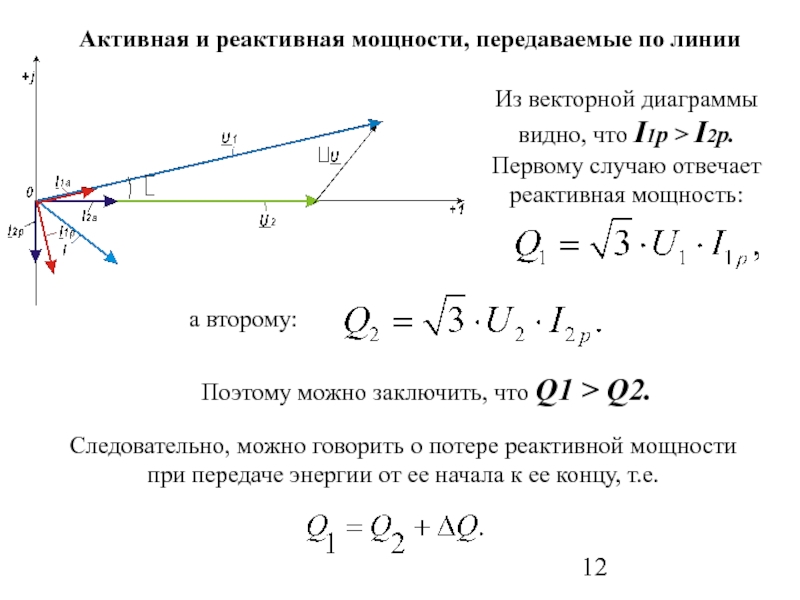
Слайд 12Из векторной диаграммы видно, что I1р > I2р.
Первому случаю отвечает реактивная
Активная и реактивная мощности, передаваемые по линии
а второму:
Поэтому можно заключить, что Q1 > Q2.
Следовательно, можно говорить о потере реактивной мощности при передаче энергии от ее начала к ее концу, т.е.
Слайд 13Однако следует помнить, что под влиянием зарядной мощности линии реактивная мощность
Т.е. Q2
Активная и реактивная мощности, передаваемые по линии
Следовательно, протекающая по линии реактивная мощность Q2, меньше, чем реактивная мощность отдаваемая нагрузке QНАГР. То же самое происходит и в начале линии QИСТ.
Слайд 14Поэтому ветви емкостной проводимости, определяющие в схеме замещения линии протекание зарядной
Активная и реактивная мощности, передаваемые по линии
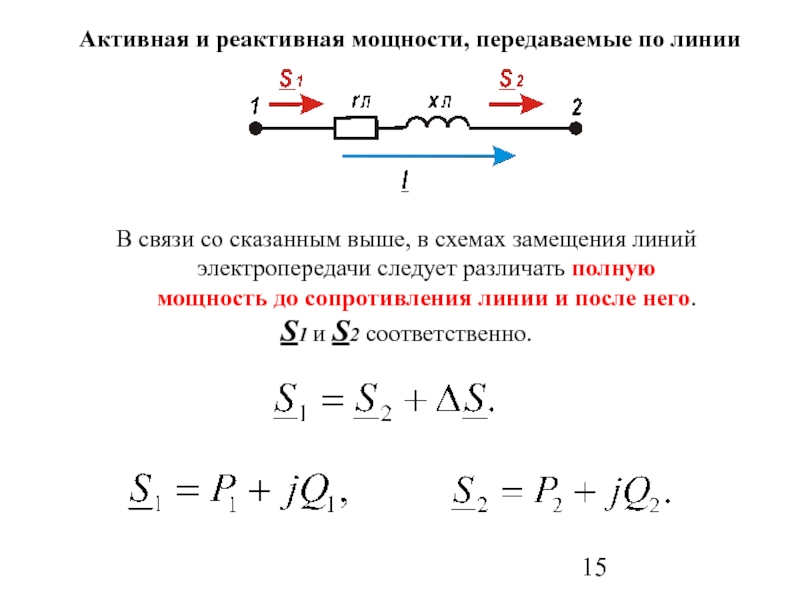
Слайд 15В связи со сказанным выше, в схемах замещения линий электропередачи следует
S1 и S2 соответственно.
Активная и реактивная мощности, передаваемые по линии
Слайд 16Классификация задач расчета линии по мощности нагрузки
все задачи расчета линии по
задача №1 – расчет по данным, приведенным к концу линии;
задача №2 - расчет по данным, приведенным к началу линии;
задача №3 – расчет при известном напряжении начала и мощности в конце линии.
Слайд 17Задача № 1 (по данным конца)
Задано:
U2; S2=P2+jQ2;
r0; x0; g0;
Необходимо определить :
U1; S1; угол между векторами напряжения в начале и в конце линии δ.
Слайд 18Задача № 1 (по данным конца)
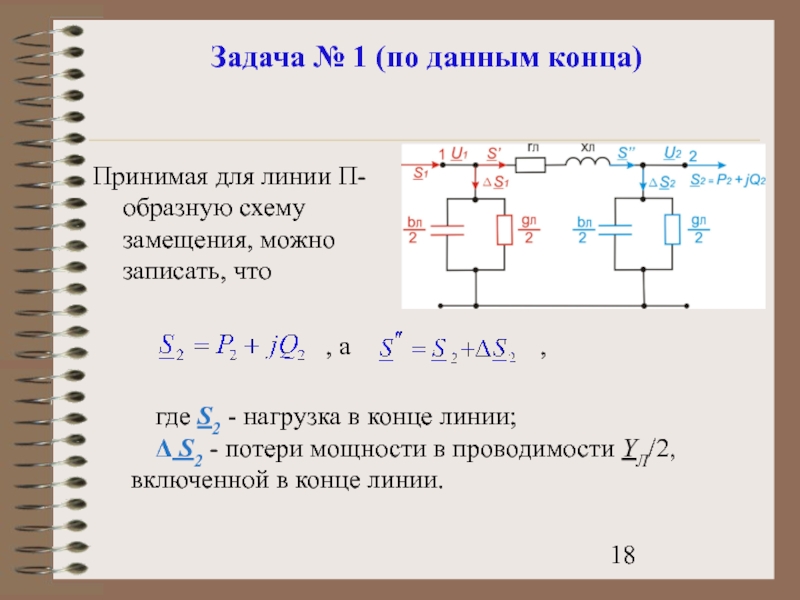
Принимая для линии П-образную схему замещения,
, а
,
где S2 - нагрузка в конце линии;
Δ S2 - потери мощности в проводимости YЛ/2, включенной в конце линии.
Слайд 19Задача № 1 (по данным конца)
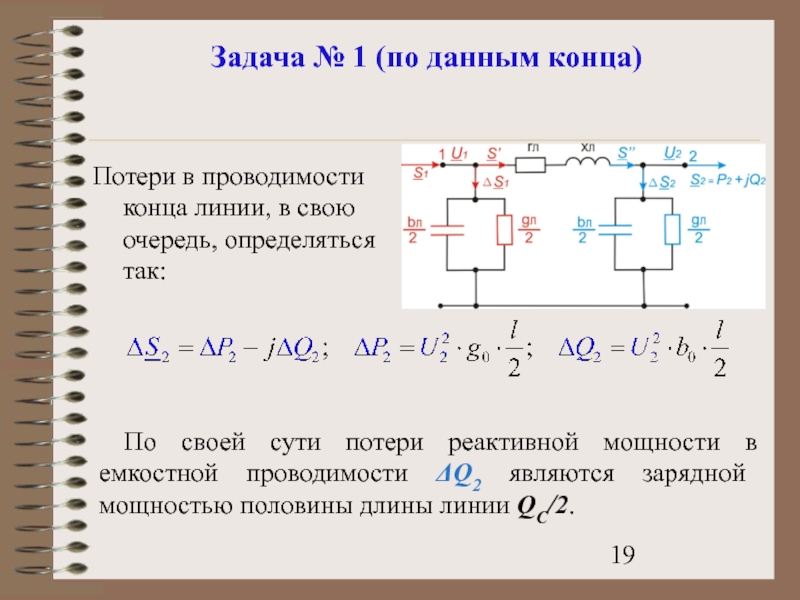
Потери в проводимости конца линии, в
По своей сути потери реактивной мощности в емкостной проводимости ΔQ2 являются зарядной мощностью половины длины линии QC/2.
Слайд 21Задача № 1 (по данным конца)
Мощность в начале линии S’ отличается
Слайд 22Задача № 1 (по данным конца)
Для определения мощности S1 необходимо к
Однако для определения указанной величины необходимо знать напряжение U1 в начале линии, т.к. под воздействием именно этого напряжения в проводимости начала линии протекает мощность ΔS1.
Слайд 23Задача № 1 (по данным конца)
Зависимость между фазными напряжениями точек 1
где ΔU2 – падение напряжения в сопротивлении линии zЛ на участке 1-2.
Тогда можно записать:
Слайд 24Задача № 1 (по данным конца)
Модуль вектора напряжения U1 можно определить
Слайд 25Задача № 1 (по данным конца)
Угол между векторами напряжения в начале
Слайд 27Задача № 2 (по данным начала)
Задано:
U1; S1=P1+jQ1;
r0; x0; g0;
Необходимо определить :
U2; S2 ; угол между векторами напряжения в начале и в конце линии δ.
Слайд 28Задача № 2 (по данным начала)
Мощность в начале линии S’ определяется
Слайд 29Задача № 2 (по данным начала)
Мощность в начале линии S’ отличается
Слайд 30Задача № 2 (по данным начала)
Напряжение в точке 2 определится как
Слайд 31Задача № 2 (по данным начала)
Модуль вектора напряжения U2 можно определить
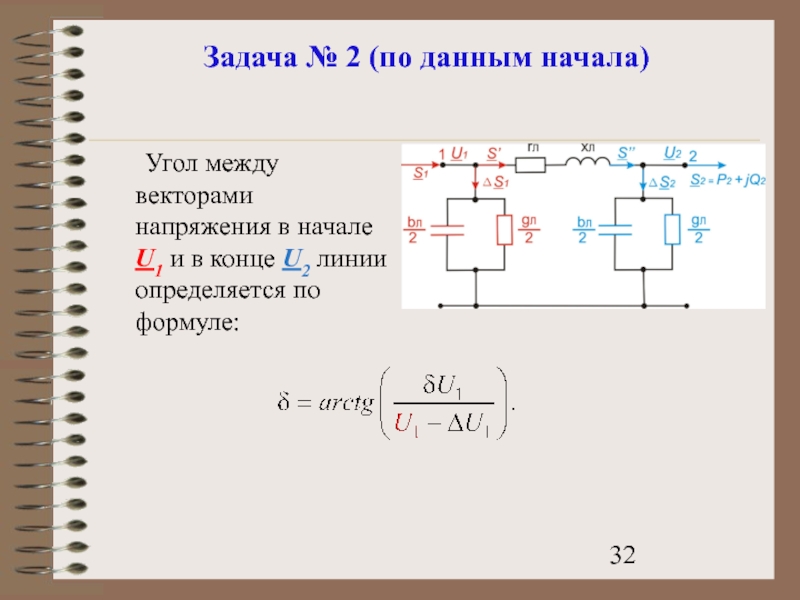
Слайд 32Задача № 2 (по данным начала)
Угол между векторами напряжения в начале
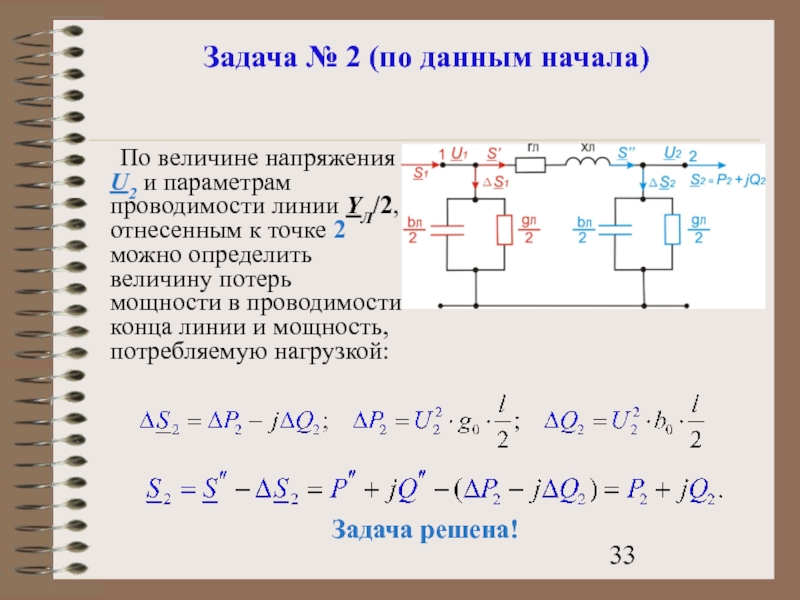
Слайд 33Задача № 2 (по данным начала)
По величине напряжения U2 и параметрам
Задача решена!
Слайд 34Задача № 3
Задано:
U1; S2=P2+jQ2;
r0; x0; g0; b0; l.
т.е. заданы
Необходимо определить :
U2; S1; угол между векторами напряжения в начале и в конце линии δ.
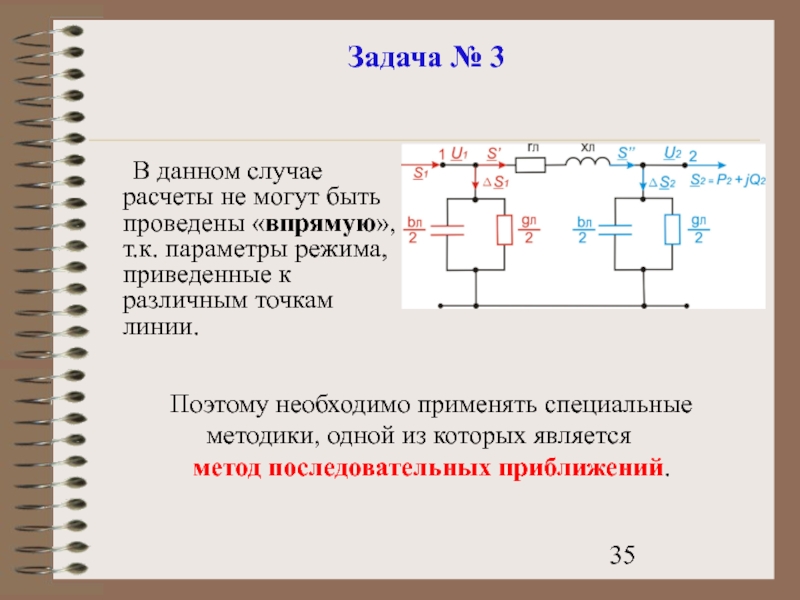
Слайд 35Задача № 3
В данном случае расчеты не могут быть проведены «впрямую»,
Поэтому необходимо применять специальные методики, одной из которых является
метод последовательных приближений.
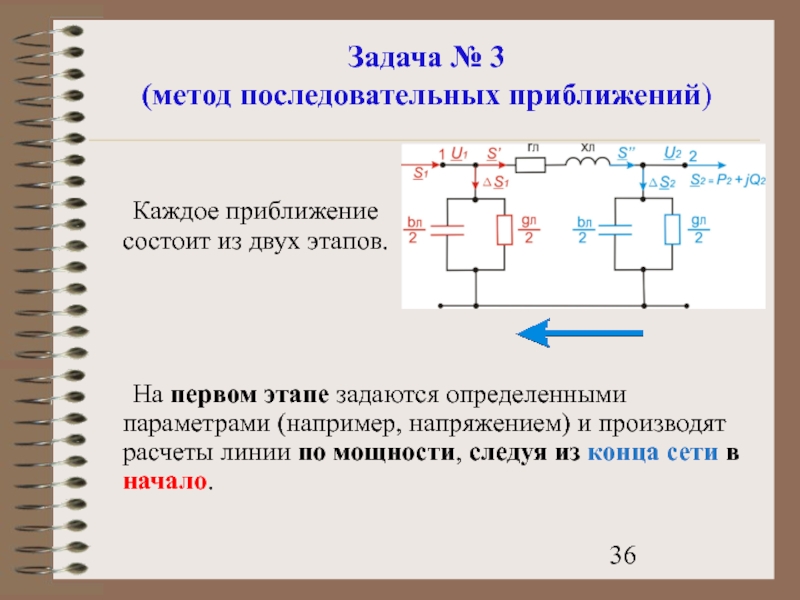
Слайд 36Задача № 3
(метод последовательных приближений)
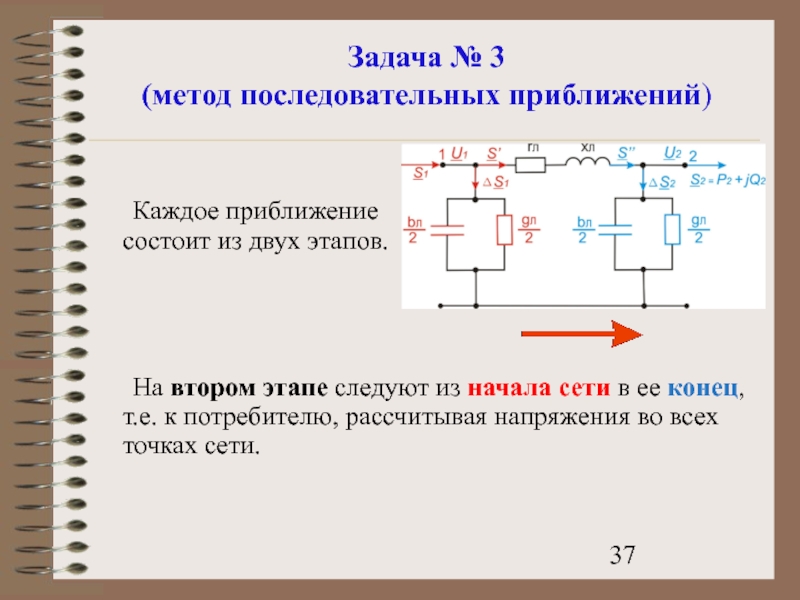
Каждое приближение состоит из двух этапов.
На
Слайд 37Задача № 3
(метод последовательных приближений)
Каждое приближение состоит из двух этапов.
На
Слайд 38Задача № 3
(метод последовательных приближений)
Так в качестве первого этапа принимается условие,
При этом условии находиться распределение мощностей в сети. Зарядные мощности и потери мощности в сопротивлениях линии определяется по номинальному напряжению UНОМ .
Слайд 39Задача № 3
(метод последовательных приближений)
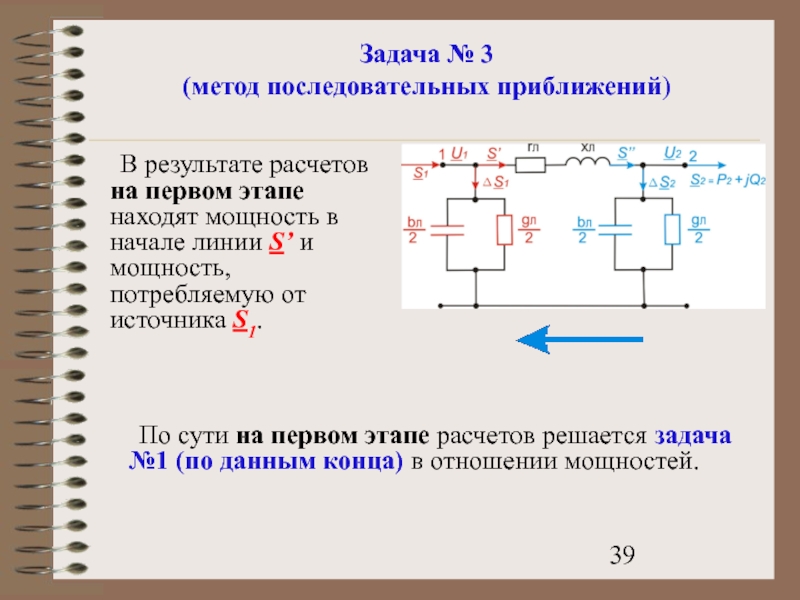
По сути на первом этапе расчетов решается
В результате расчетов на первом этапе находят мощность в начале линии S’ и мощность, потребляемую от источника S1.
Слайд 40Задача № 3
(метод последовательных приближений)
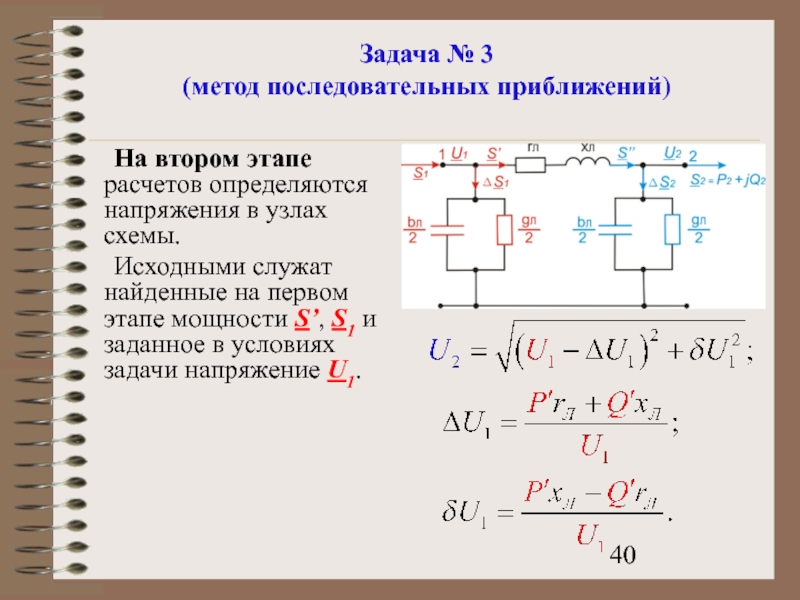
На втором этапе расчетов определяются напряжения в
Исходными служат найденные на первом этапе мощности S’, S1 и заданное в условиях задачи напряжение U1.
Слайд 41Задача № 3
(метод последовательных приближений)
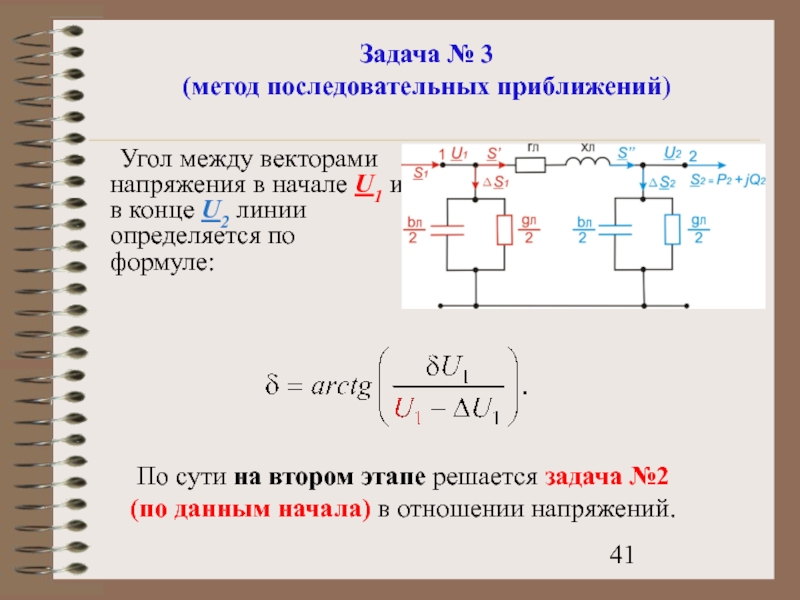
Угол между векторами напряжения в начале U1
По сути на втором этапе решается задача №2
(по данным начала) в отношении напряжений.
Слайд 42Задача № 3
(метод последовательных приближений)
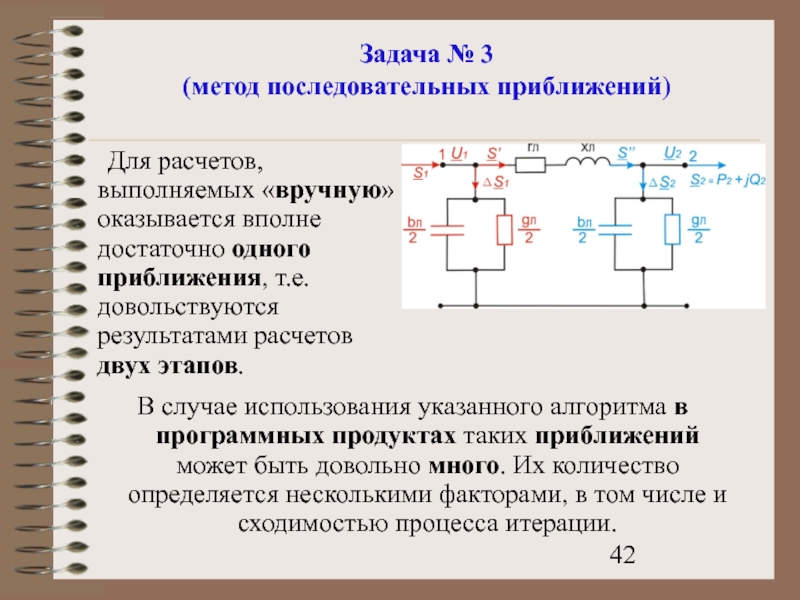
Для расчетов, выполняемых «вручную» оказывается вполне достаточно
В случае использования указанного алгоритма в программных продуктах таких приближений может быть довольно много. Их количество определяется несколькими факторами, в том числе и сходимостью процесса итерации.
Слайд 43Понятие расчетных нагрузок подстанций (узлов).
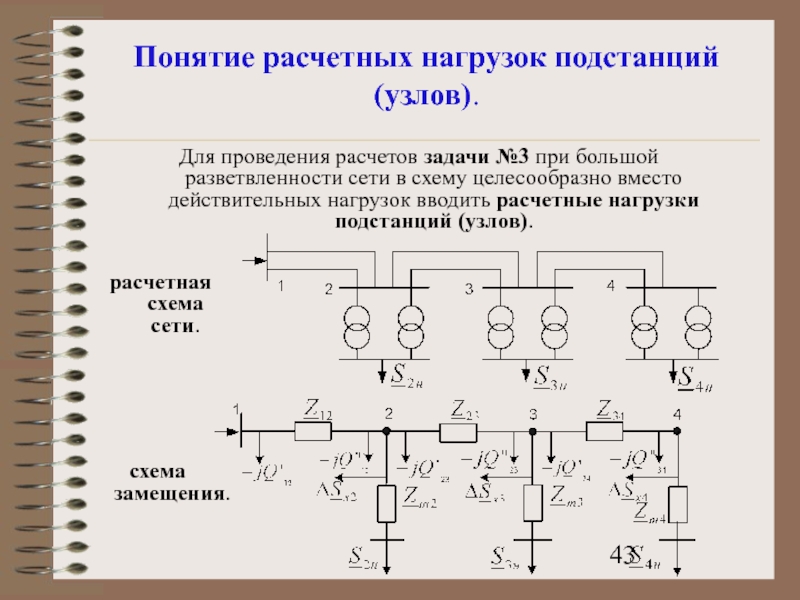
Для проведения расчетов задачи №3 при большой
расчетная схема сети.
схема замещения.
Слайд 45Понятие расчетных нагрузок подстанций (узлов).
Расчетная нагрузка для подстанции №2 определяется:
Слайд 46Понятие расчетных нагрузок подстанций (узлов).
Расчетная нагрузка для подстанции №3 определяется:
Слайд 47Понятие расчетных нагрузок подстанций (узлов).
Расчетная нагрузка для подстанции №4 определяется:
Слайд 49Понятие расчетных нагрузок подстанций (узлов).
Таким образом, расчетная нагрузка подстанции включает помимо
Использование расчетных нагрузок существенно упрощает расчет, но введение расчетной нагрузки приводит к определенной погрешности в расчетах.
Это связано с тем, что при определении потерь мощности в элементах сети ΔS и величины QC линий используется номинальное напряжение UНОМ, вместо неизвестных напряжений в узловых точках. Однако эта погрешность находится в диапазоне допустимых значений для ручного расчета.
Слайд 50Задача № 3
(метод систематизированного подбора)
Существуют задачи, в которых необходим более строгий
Слайд 51Задача № 3
(метод систематизированного подбора)
Известными являются параметры линий, а также напряжение
Необходимо определить SA , а также напряжения U1 и U2.
Слайд 52Задача № 3
(метод систематизированного подбора)
В данном случае, расчеты не могут быть
Однако такие расчеты окажутся громоздкими, а возможно, решение не будет найдено вообще.
Слайд 53Задача № 3
(метод систематизированного подбора)
Данное обстоятельство объясняется необходимостью учета изменения мощностей
При ручном счете более целесообразно решать задачу методом систематизированного подбора.
Слайд 54Задача № 3
(метод систематизированного подбора)
Суть метода систематизированного подбора, заключается в следующем:
1. Задаются произвольно значением напряжения в точке 2 U2(1).
Слайд 55Задача № 3
(метод систематизированного подбора)
2. По статической характеристике
определяют мощность нагрузки:
Слайд 56Задача № 3
(метод систематизированного подбора)
Далее расчет ведут по алгоритму задачи №1,
Слайд 57Задача № 3
(метод систематизированного подбора)
3. По напряжению U2(1) определяют мощность, обусловленную
Слайд 58Задача № 3
(метод систематизированного подбора)
4. По этим данным определяют мощность в
Слайд 59Задача № 3
(метод систематизированного подбора)
5. Тогда напряжение в точке 1 U1(1)
Слайд 60Задача № 3
(метод систематизированного подбора)
6. Потери мощности на участке 1-2 и
Слайд 61Задача № 3
(метод систематизированного подбора)
6. Потери мощности на участке 1-2 и
Слайд 62Задача № 3
(метод систематизированного подбора)
7. Зарядные мощности начала участка 1-2 и
Слайд 63Задача № 3
(метод систематизированного подбора)
8. По статической характеристике
определяют мощность нагрузки:
Слайд 65Задача № 3
(метод систематизированного подбора)
9. Аналогичные расчеты проводят для участка А-1.
Слайд 68Задача № 3
(метод систематизированного подбора)
10. В результате определяют величину напряжения в
Слайд 69Задача № 3
(метод систематизированного подбора)
Обычно достаточно задаться тремя значениями напряжения для
Точность результатов расчета таким методом определяется количеством полученных в ходе расчетов точек.
Слайд 70Задача № 3
(метод систематизированного подбора)
По найденным значениям напряжений U2иск и U1иск
Слайд 71Источники дополнительных сведений
Идельчик В.И. Электрические системы и сети. - М.: Энергоатомиздат,
Электрические системы. Т. 2. Электрические сети/ Под ред. В.А. Веникова. - М.: Высшая школа, 1971. - 440 с.
Герасименко А. А., Федин В.Т. Передача и распределение электрической энергии. – изд.2-е. – Ростов н/Д : Феникс, 2008. – 715, [2] с. – (Высшее образование)
Боровиков В.А. и др. Электрические сети энергетических систем. Изд. 3-е, переработанное. Л., «Энергия», 1977.
Черепанова Г.А., Вычегжанин А.В. Установившиеся режимы электрических сетей в примерах и задачах. - Киров: изд. ВятГУ, 2009 - 114 с.