- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Работа и мощность силы. Консервативные силы, работа консервативных сил. Потенциальная и кинетическая энергия презентация
Содержание
- 1. Работа и мощность силы. Консервативные силы, работа консервативных сил. Потенциальная и кинетическая энергия
- 2. Энергия — универсальная мера различных форм движения
- 3. Пусть на материальную точку действует сила F,
- 4. Работа А – величина алгебраическая: в зависимости
- 5. На практике часто имеет значение не само
- 6. Если в каждой точке пространства на помещенную
- 7. Потенциальная энергия — механическая энергия системы тел,
- 8. Тот факт, что работа консервативных сил зависит
- 9. Для этого достаточно вычислить работу, совершаемую силами
- 10. При перемещении материальной точки из одной точки
- 11. Найдем элементарную работу, которую совершает эта сила
- 12. Результирующая всех сил может быть представлена как
- 13. Закон сохранения энергии Полная механическая энергия, как
- 14. Если же рассматривать не одну материальную точку,
- 15. Механические системы, на тела которых действуют только
- 16. «энергия никогда не исчезает и не появляется
- 17. Закон сохранения импульса
- 18. Законы сохранения. Воспользовавшись определением импульса, запишем
- 19. Законы сохранения. Материальные точек, входящие в
- 20. Законы сохранения. Рассмотрим импульс системы состоящей
- 21. Законы сохранения. Если на систему не
- 22. Упругие и неупругие соударения Уда́р — толчок,
- 23. Абсолютно упругий удар — модель соударения, при которой
- 24. Абсолютно упругие удары при различных условиях
- 25. Для математического описания простейших абсолютно упругих ударов,
- 26. Абсолютно неупругим ударом называют такое ударное взаимодействие,
- 27. Удар (или соударение)—это столкновение двух или более
- 28. Закон сохранения механической энергии: Закон сохранения импульса: Для абсолютно упругого удара справедливы законы:
- 29. Решая совместно два уравнения, получим выражения для скорости тел после удара:
- 30. Абсолютно неупругий удар Закон сохранения импульса: В
- 31. Вследствие деформации происходит «потеря» кинетической энергии, перешедшей
- 32. Замкнутой (изолированной) называется такая механическая система тел,
- 33. Центром масс (или центром инерции) системы материальных
- 34. Скорость центра масс: Учитывая, что pi =
- 35. т. е. центр масс системы движется как
- 37. Законы сохранения. 4.6 Момент импульса относительно точки
- 38. Законы сохранения. 4.7 Момент импульса материальной точки
- 39. Законы сохранения. 4.8 Модуль этого вектора равен
- 40. Законы сохранения. 4.9 Для определения приращения момента
- 41. Законы сохранения. 4.10 Момент внутренней силы действующей
- 42. Законы сохранения. 4.11 Радиус-вектор r12 коллинеарен силе
Слайд 2Энергия — универсальная мера различных форм движения и взаимодействия.
Энергия бывает:
Работа силы – количественная характеристика процесса обмена энергией между взаимодействующими телами.
Если тело движется прямолинейно и на него действует постоянная сила F, которая составляет некоторый угол a с направлением перемещения, то работа этой силы:
Лекция 5
Работа и мощность силы. Консервативные силы, работа консервативных сил. Потенциальная и кинетическая энергия
Слайд 3Пусть на материальную точку действует сила F, и под действием этой
Действие силы F на перемещении dr характеризуют величиной, равной скалярному произведению Fdr, эту величину называю работой силы F на перемещении dr:
где α – угол между вектором силы и перемещения, ds – элементарный отрезок пути, Fs – проекция вектора силы на перемещение.
При криволинейном движении сила может изменяться как по модулю, так и по направлению.
Работа. Мощность. Энергия.
Слайд 4Работа А – величина алгебраическая: в зависимости от угла между силой
Построив график зависимости проекции силы Fs от положения материальной точки (s) на траектории. Можно придти к выводу, что графически элементарная работа dA будет выглядеть как площадь под графиком между двумя точками. При этом площадь над осью s будет положительной, а под ней отрицательной.
Единица работы — джоуль (Дж):
1 Дж — работа, совершаемая силой 1 Н на пути 1 м (1 Дж=1 Н ⋅ м).
Работа. Мощность. Энергия.
Слайд 5На практике часто имеет значение не само значение работы, а то
величина, характеризующая работу, совершаемую в единицу времени – мощность.
Если работа, совершаемая за одинаковые промежутки времени не одинакова то можно определить мгновенную мощность:
Пусть за время dt точка получает перемещение dr. Тогда элементарная работа равна dA=Fdr и мощность можно представить в виде:
Единица мощности — ватт (Вт): 1 Вт — мощность, при которой за время 1 с совершается работа 1 Дж (1 Вт = 1 Дж/с).
Работа. Мощность. Энергия.
Слайд 6Если в каждой точке пространства на помещенную туда материальную точку действует
Поле, остающееся постоянным во времени, называют стационарным.
Стационарные силовые поля, в которых работа не зависит от пути между точками 1 и 2, называют консервативными.
Силы, не являющиеся консервативными, называют неконсервативными или диссипативными.
Силы, зависящие только от расстояния между взаимодействующими частицами и направленные по прямой, проходящей через эти частицы называют центральными
Работа. Мощность. Энергия.
Слайд 7Потенциальная энергия — механическая энергия системы тел, определяемая их взаимным расположением
Потенциальная энергия есть функция состояния системы. Она зависит только от конфигурации системы и от ее положения по отношению к внешним телам.
Примеры потенциальной энергии.
1. Потенциальная энергия тела массой m, поднятого над землей на высоту h:
2. Потенциальная энергия пружины, растянутой на длину x :
Работа. Мощность. Энергия.
Слайд 8Тот факт, что работа консервативных сил зависит только от начального и
Работа. Мощность. Энергия.
Таким образом, работа сил поля на пути 1-2 равна убыли потенциальной энергии материальной точки в данном поле.
Слайд 9Для этого достаточно вычислить работу, совершаемую силами поля на любом пути
В поле упругой силы:
В кулоновском поле материальной точки:
В однородном поле силы тяжести:
Работа. Мощность. Энергия.
Слайд 10При перемещении материальной точки из одной точки поля консервативных сил в
Так как Fdr=Fsds имеем:
Отсюда:
В декартовых координатах это соотношение имеет вид:
Величину, стоящую в скобках, называют градиентом скалярной функции U и обозначают grad U или
Работа. Мощность. Энергия.
Слайд 11Найдем элементарную работу, которую совершает эта сила при элементарном перемещении dr
Отсюда видно, что работа результирующей силы F идет на приращение некоторой величины, которую называют кинетической энергией:
Таким образом, при конечном перемещении из точки 1 в точку 2:
приращение кинетической энергии частицы на некотором перемещении равно алгебраической сумме работ всех сил, действующих на материальную точку на том же перемещении.
Работа. Мощность. Энергия.
Слайд 12Результирующая всех сил может быть представлена как
F=Fконс.+Fстор.
Тогда работа этих
Аконс.+Астор.
Так же работа сил консервативного поля равна убыли потенциальной энергии
Аконс.=-ΔU.
В итоге получаем:
ΔT=-ΔU+Aстор.
Δ(T+U)=Астор.
Из этого соотношения видно, что работа сторонних сил идет на приращение величины
T+U.
Эту величину – сумму кинетической и потенциальной энергий – называют полной механической энергией материальной точки и обозначают Е.
Работа. Мощность. Энергия.
Слайд 13Закон сохранения энергии
Полная механическая энергия, как и потенциальная, определяется с точностью
Изменение полной механической энергии материальной точки обусловлено совершением над ней работы сторонними силами. Отсюда непосредственно следует закон сохранения механической энергии: если сторонние силы отсутствуют или таковы, что не совершают работы в течении интересующего нас времени, то полная механическая энергия частицы в стационарном поле консервативных сил остается постоянной за это время.
Лекция 6.
Закон сохранения энергии. Закон сохранения импульса. Момент импульса, закон сохранения момента импульса.
Слайд 14Если же рассматривать не одну материальную точку, а систему, то помимо
Механическая энергия замкнутой системы, в которой не действуют диссипативные силы, сохраняется в процессе движения т.е
Законы сохранения.
Слайд 15Механические системы, на тела которых действуют только консервативные силы (внутренние и
Закон сохранения механической энергии можно сформулировать еще так:
«в консервативных системах полная механическая энергия сохраняется».
Диссипативные системы – это такие, в которых механическая энергия постепенно уменьшается за счет преобразования в другие формы энергии.
Процесс уменьшения механической энергии за счет преобразования в другие формы энергии получил название диссипации (или рассеяния) энергии.
Законы сохранения.
Слайд 16«энергия никогда не исчезает и не появляется вновь, она лишь превращается
Закон сохранения и превращения энергии — фундаментальный закон природы:
В этом и заключается физическая сущность закона сохранения и превращения энергии — сущность неуничтожимости материи и ее движения.
Законы сохранения.
Слайд 17 Закон сохранения импульса
Любое тело или совокупность тел
По определению, импульс материальной точки:
где m и v – ее масса и скорость.
Законы сохранения.
Слайд 18Законы сохранения.
Воспользовавшись определением импульса, запишем второй закон Ньютона в иной
т.е. производная импульса материальной точки по времени равна результирующей всех сил действующих на материальную точку. Например если F=0 то p=const.
Это уравнение позволяет найти приращение импульса материальной точки за любой промежуток времени, если известна зависимость силы F от времени:
Таким образом, приращение импульса частицы за любой промежуток времени зависит не только от значения силы, но и от продолжительности ее действия
Слайд 19Законы сохранения.
Материальные точек, входящие в систему могут взаимодействовать, как между
силы взаимодействия между материальными точками системы называются внутренними,
а силы обусловленные взаимодействием с телами не входящими в систему называются внешними.
В случае если на систему не действуют внешние силы, она называется замкнутой.
Импульс системы определим, как векторную сумму импульсов ее отдельных частей:
Слайд 20Законы сохранения.
Рассмотрим импульс системы состоящей из двх материальных точек. Тогда
Сложим эти два уравнения вместе. Сумма внутренних сил будет равна нулю (по третьему закону Ньютона, F12=-F21), вследствие чего получим:
Слайд 21Законы сохранения.
Если на систему не действуют внешние силы то получается,
следовательно для замкнутой системы р постоянен.
Аналогичные рассуждения можно обобщить и на систему из N материальных точек. Закон сохранения импульса формулируется следующим образом:
импульс замкнутой системы материальных точек остается постоянным.
Импульс остается постоянным и для не замкнутой системы при условии, что внешние силы, действующие на материальные точки системы, в сумме дают ноль. Даже если сумма внешних сил не равна нулю, но проекция этой суммы на некоторую ось равна нулю, то проекция импульса системы на эту ось будет оставаться постоянной.
Слайд 22Упругие и неупругие соударения
Уда́р — толчок, кратковременное взаимодействие тел, при котором происходит
Применение законов сохранения энергии и импульса во многих случаях позволяет исключить из рассмотрения сам процесс столкновения и получить связь между скоростями тел до и после столкновения, минуя все промежуточные значения этих величин.
В механике часто используются две модели ударного взаимодействия – абсолютно упругий и абсолютно неупругий удары.
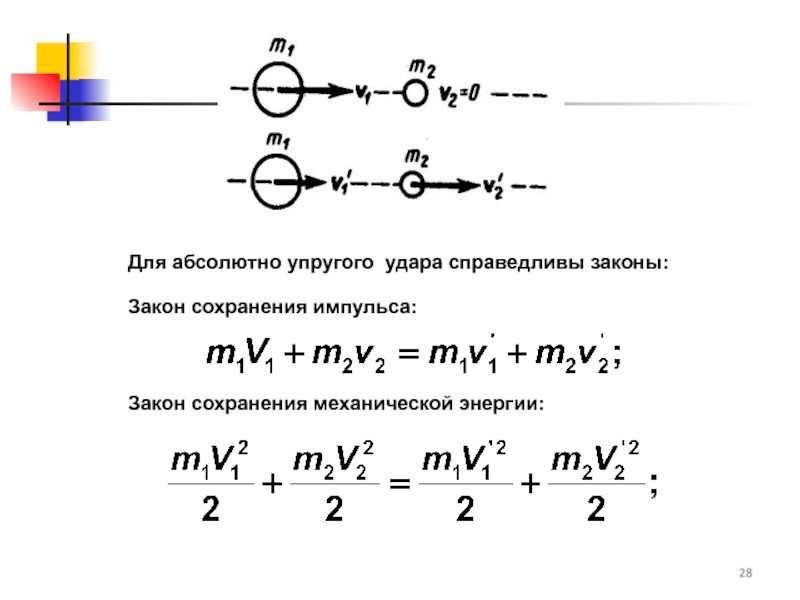
Слайд 23Абсолютно упругий удар — модель соударения, при которой полная кинетическая энергия системы
1. Есть в наличии два абсолютно твердых тела, которые сталкиваются
2. В точке контакта происходят упругие деформации. Кинетическая энергия движущихся тел мгновенно переходит в энергию деформации.
3. В следующий момент деформированные тела принимают свою прежнюю форму, а энергия деформации вновь переходит в кинетическую энергию.
4. Контакт тел прекращается и они продолжают движение.
Слайд 25Для математического описания простейших абсолютно упругих ударов, используется закон сохранения энергии
Здесь m1, m2 - массы первого и второго тел. u1, v1 - скорость первого тела до, и после взаимодействия. u2, v2 - скорость второго тела до, и после взаимодействия.
Важно, что импульсы складываются векторно, а энергии скалярно.
Законы абсолютно упругого удара могут выполняться совершенно точно при столкновениях элементарных частиц низких энергий. Это следствие принципов квантовой механики, запрещающей произвольные изменения энергии системы. Если энергии сталкивающихся частиц недостаточно для возбуждения их внутренних степеней свободы, то механическая энергия системы не меняется.
Слайд 26Абсолютно неупругим ударом называют такое ударное взаимодействие, при котором тела соединяются
При абсолютно неупругом ударе механическая энергия не сохраняется. Она частично или полностью переходит во внутреннюю энергию тел (нагревание).
При абсолютно неупругом ударе импульс сохраняется согласно соотношению
где v - это общая скорость тел, полученная после удара, ma - масса первого тела, ua - скорость первого тела до соударения, mb - масса второго тела, ub -скорость второго тела до соударения. Важно, что импульсы являются величинами векторными, поэтому складываются только векторно.
Слайд 27Удар (или соударение)—это столкновение двух или более тел, при котором взаимодействие
Центральный удар – такой, если тела до удара движутся вдоль прямой, проходящей через их центры масс.
Определения:
Абсолютно упругий удар — столкновение двух тел, в результате которого в обоих взаимодействующих телах не остается никаких деформаций и вся кинетическая энергия, которой обладали тела до удара, после удара снова превращается в кинетическую энергию.
Абсолютно неупругий удар — столкновение двух тел, в результате которого тела объединяются, двигаясь дальше как единое целое.
3.3. Соударения тел
Слайд 28Закон сохранения механической энергии:
Закон сохранения импульса:
Для абсолютно упругого удара справедливы законы:
Слайд 30Абсолютно неупругий удар
Закон сохранения импульса:
В частном случае, если массы шаров равны
Если ударяемое тело было первоначально неподвижно (v2=0), то
Слайд 31Вследствие деформации происходит «потеря» кинетической энергии, перешедшей в тепловую или другие
Если ударяемое тело было первоначально неподвижно (v2=0), то
Слайд 32Замкнутой (изолированной) называется такая механическая система тел, на которую не действуют
«Импульс в замкнутой системе не изменяется с течением времени».
Закон сохранения импульса является следствием однородности пространства:
при параллельном переносе в пространстве замкнутой системы тел как целого ее физические свойства не изменяются.
Слайд 33Центром масс (или центром инерции) системы материальных точек называется воображаемая точка
— радиус-вектор системы,
где mi и ri — соответственно масса и радиус-вектор i-й материальной точки;
n — число материальных точек в системе.
— масса системы.
Закон движения центра масс.
Слайд 34Скорость центра масс:
Учитывая, что pi = mivi , a
есть импульс
Импульс системы равен произведению массы системы на скорость ее центра масс.
записать:
Слайд 35т. е. центр масс системы движется как материальная точка, в которой
Закон движения центра масс:
«центр масс замкнутой системы либо движется прямолинейно и равномерно, либо остается неподвижным».
Слайд 37Законы сохранения. 4.6
Момент импульса относительно точки О равен:
где r – радиус-вектор,
где α – угол между r и р, l=rsinα – плечо вектора р относительно точки О
Слайд 38Законы сохранения. 4.7
Момент импульса материальной точки может изменяться со временем, продифференцировав
Первое слагаемое в правой части равенства обращается в ноль так, как dr/dt=v, а скорость параллельна импульсу р. Далее, согласно второму закону Ньютона, dp/dt=F, получаем:
Величину, стоящую в правой части этого уравнения, называют моментом силы F относительно точки О. Обозначим ее буквой М:
Слайд 39Законы сохранения. 4.8
Модуль этого вектора равен
M=lF.
Таким образом производная от
Это уравнение называют уравнением моментов. Из уравнения моментов, в частности, следует, что если М=0, то L=const. Другими словами, если относительно некоторой точки О выбранной системы отсчета момент всех сил, действующих на частицу, равен нулю в течение интересующего нас промежутка времени, то относительно этой точки момент импульса частицы остается постоянным в течение этого времени.
Слайд 40Законы сохранения. 4.9
Для определения приращения момента импульса частицы относительно точки О
Момент импульса системы - векторная сумма моментов импульсов ее отдельных частиц:
Подобно тому, как это делалось для импульса системы. Рассмотрим случай системы состоящей из двух материальных точек.
Слайд 41Законы сохранения. 4.10
Момент внутренней силы действующей на 1 частицу со стороны
Сложив эти выражения получим:
Рассмотрим сумму двух первых слагаемых в правой части :
Слайд 42Законы сохранения. 4.11
Радиус-вектор r12 коллинеарен силе F12, поэтому векторное произведение этих
Данное соотношение можно обобщить на систему из произвольного числа материальных точек. Следовательно, получаем, что изменение момента импульса системы обусловлено действием на нее момента внешних сил. Если же внешние силы не действуют, то момент импульса остается постоянным. Таким образом, мы пришли к закону сохранения момента импульса:
момент импульса замкнутой системы материальных точек остается постоянным.