- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Прямолинейные колебания точки презентация
Содержание
- 1. Прямолинейные колебания точки
- 2. КОЛЕБАНИЯ Колебания Осциллятор — система, совершающая колебания движения точки,
- 3. ЦЕЛЬ ЛЕКЦИИ Колебания На примере прямолинейных колебаний
- 4. КОЛЕБАНИЯ В СТРОИТЕЛЬСТВЕ Колебания
- 5. СВОБОДНЫЕ КОЛЕБАНИЯ Свободные колебания
- 6. СВОБОДНЫЕ КОЛЕБАНИЯ Свободные колебания
- 7. СВОБОДНЫЕ КОЛЕБАНИЯ Свободные колебания
- 8. СВОБОДНЫЕ КОЛЕБАНИЯ Свободные колебания
- 9. СВОБОДНЫЕ КОЛЕБАНИЯ Свободные колебания
- 10. СВОБОДНЫЕ КОЛЕБАНИЯ Свободные колебания
- 11. СВОБОДНЫЕ КОЛЕБАНИЯ Свободные колебания
- 12. СВОБОДНЫЕ КОЛЕБАНИЯ Свободные колебания
- 13. СВОБОДНЫЕ КОЛЕБАНИЯ Свободные колебания
- 14. СВОБОДНЫЕ КОЛЕБАНИЯ Свободные колебания
- 15. СВОБОДНЫЕ КОЛЕБАНИЯ С ПОСТОЯННОЙ СИЛОЙ Свободные колебания
Слайд 2КОЛЕБАНИЯ
Колебания
Осциллятор — система, совершающая колебания
движения точки, которые характеризуются определенной повторяемостью по времени.
Линейный
Слайд 3ЦЕЛЬ ЛЕКЦИИ
Колебания
На примере прямолинейных колебаний точки познакомиться с колебательным движением в
Физические явления:
- механические колебания
электромагнитные волны (оптические, радио, инфракрасные…)
акустические волны (звук)
Природные явления:
суточное вращение Земли
землетрясения
приливы и отливы
Биологические системы:
сердечно-сосудистая система
ухо + голосовые связки
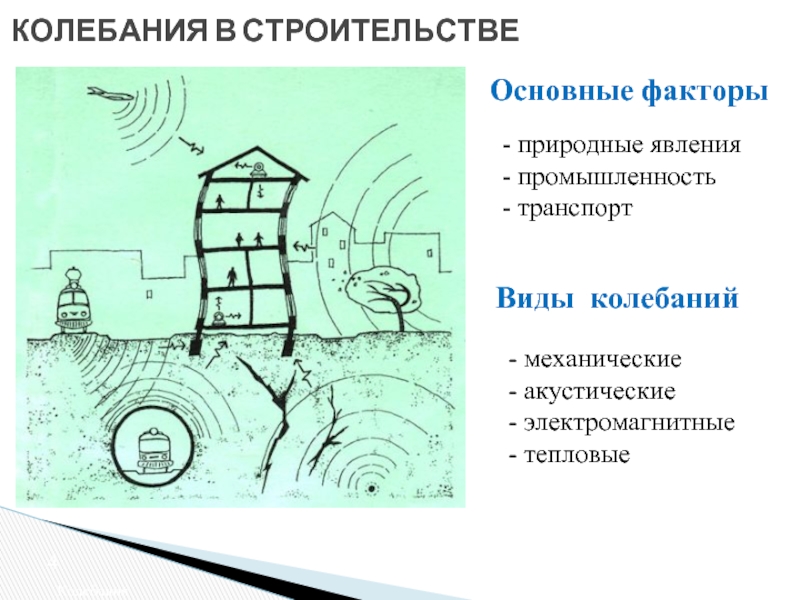
Слайд 4КОЛЕБАНИЯ В СТРОИТЕЛЬСТВЕ
Колебания
Основные факторы
- природные явления
- промышленность
- транспорт
Виды колебаний
- механические
- акустические
-
- тепловые
Слайд 5СВОБОДНЫЕ КОЛЕБАНИЯ
Свободные колебания
Начнем изучение колебаний с простой задачи. Будем рассматривать прямолинейные
Колебания называются свободными, если отсутствует внешнее воздействие на колебательную систему.
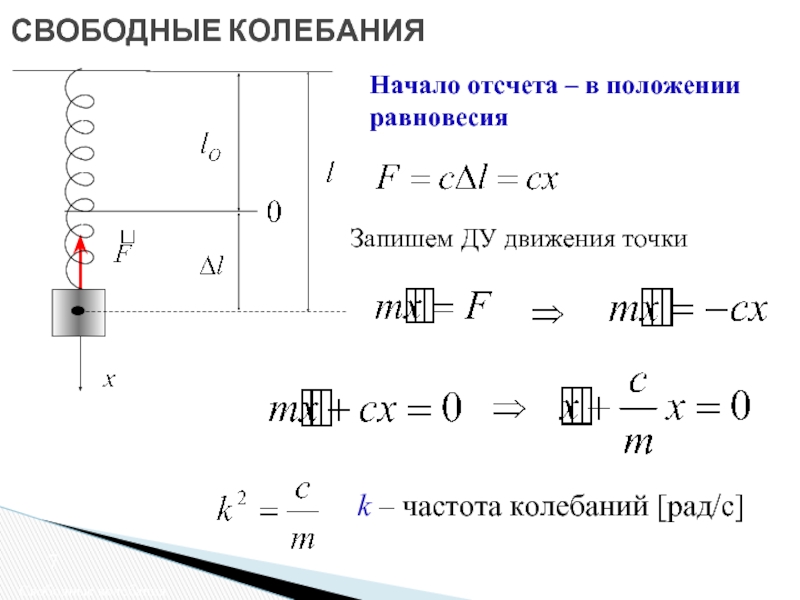
F - восстанавливающая сила
- длина недеформированной пружины
- длина деформированной пружины
- деформация пружины
Слайд 6СВОБОДНЫЕ КОЛЕБАНИЯ
Свободные колебания
c - коэффициент жесткости
пружины
Рассматриваем прямолинейное движение точки массой
Силу тяжести не учитываем.
- закон Гука
Закон Гука справедлив только для малых колебаний! В общем случае
Слайд 7СВОБОДНЫЕ КОЛЕБАНИЯ
Свободные колебания
Начало отсчета – в положении равновесия
Запишем ДУ движения точки
k – частота колебаний [рад/c]
Слайд 8СВОБОДНЫЕ КОЛЕБАНИЯ
Свободные колебания
ДУ свободных колебаний
при отсутствии сил сопротивления
линейноe
однородное
второго порядка
В результате подстановки решения получим
характеристическое уравнение
Слайд 9СВОБОДНЫЕ КОЛЕБАНИЯ
Свободные колебания
Корни уравнения мнимые
используя формулу Эйлера
- постоянные интегрирования
Можно получить другую
если ввести две другие постоянные
Слайд 10СВОБОДНЫЕ КОЛЕБАНИЯ
Свободные колебания
Воспользуемся тригонометрической формулой
Получим решение уравнения свободных колебаний в форме
-
Слайд 11СВОБОДНЫЕ КОЛЕБАНИЯ
Свободные колебания
амплитуда колебаний [м]
фаза колебаний [радиан]
начальная фаза
Колебания, описываемые этим уравнением, называются гармоническими.
Слайд 12СВОБОДНЫЕ КОЛЕБАНИЯ
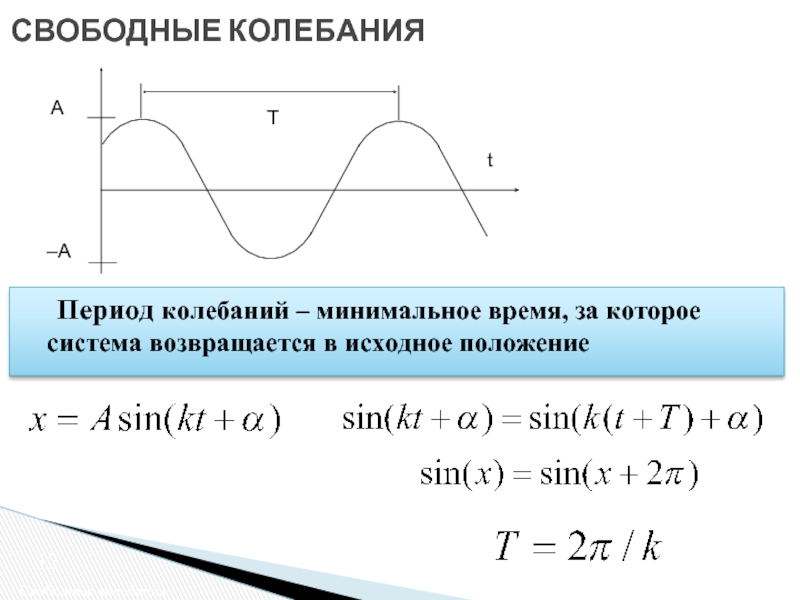
Свободные колебания
Период колебаний – минимальное время, за которое система возвращается
Слайд 13СВОБОДНЫЕ КОЛЕБАНИЯ
Свободные колебания
Подставим начальные условия
в общее решение
Получим
Найдем постоянные интегрирования
Слайд 14СВОБОДНЫЕ КОЛЕБАНИЯ
Свободные колебания
1. Амплитуда и начальная фаза колебаний зависят от начальных
2. Частота и период колебаний не зависят от начальных условий задачи и полностью определяются параметрами самой колебательной системы
Слайд 15СВОБОДНЫЕ КОЛЕБАНИЯ С ПОСТОЯННОЙ СИЛОЙ
Свободные колебания
Рассматриваем прямолинейное движение точки массой m.
Силу
Условие равновесия
Постоянная сила, не изменяя характер колебаний, смещает центр колебаний в сторону ее действия на величину статической деформации
