- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Пространственная система сил. (Тема 1.5) презентация
Содержание
- 1. Пространственная система сил. (Тема 1.5)
- 2. Студент должен: иметь представление: - о
- 3. Знать: - момент силы
- 4. Уметь: -выполнять разложение силы на
- 5. Пространственная система сил-
- 6. 1. Пространственная системой сходящихся сил (пространственный пучок
- 7. Теорема о равнодействующей пространственной ССС.
- 8. Способы определения равнодействующей силы пространственной системы сходящихся
- 9. Проекция силы на ось в пространстве
- 10. Проекция силы на ось в пространстве б)
- 11. Разложение силы по трём осям координат
- 12. Модуль и направление равнодействующей силы : -
- 13. Аналитическое условие равновесия пространственной ССС
- 14. 2 МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ОСИ
- 15. Правило знаков Момент
- 16. Момент силы относительно оси равен нулю в
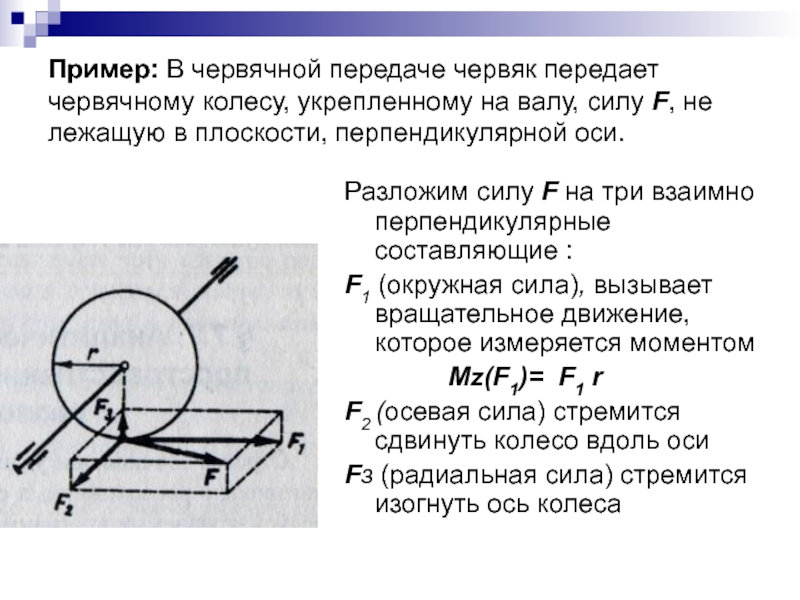
- 17. Пример: В червячной передаче червяк передает червячному
- 18. 3. Пространственная система произвольно расположенных сил
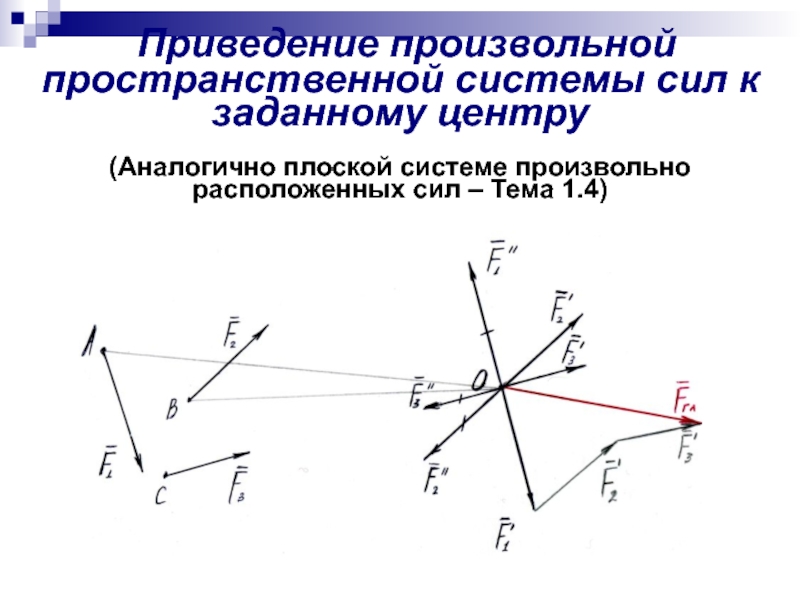
- 19. Приведение произвольной пространственной системы
- 20. Приведение произвольной пространственной системы
- 21. Модуль и направление главного вектора : -
- 22. Модуль главного момента : Алгебраическая сумма
- 23. Аналитические условия равновесия пространственной системы
Слайд 3 Знать: - момент силы относительно оси, свойства момента; - аналитический способ определения
Слайд 4 Уметь: -выполнять разложение силы на три взаимно перпендикулярные оси; -определять момент силы относительно
Слайд 5Пространственная
система сил-
система сил, линии действия которых расположены
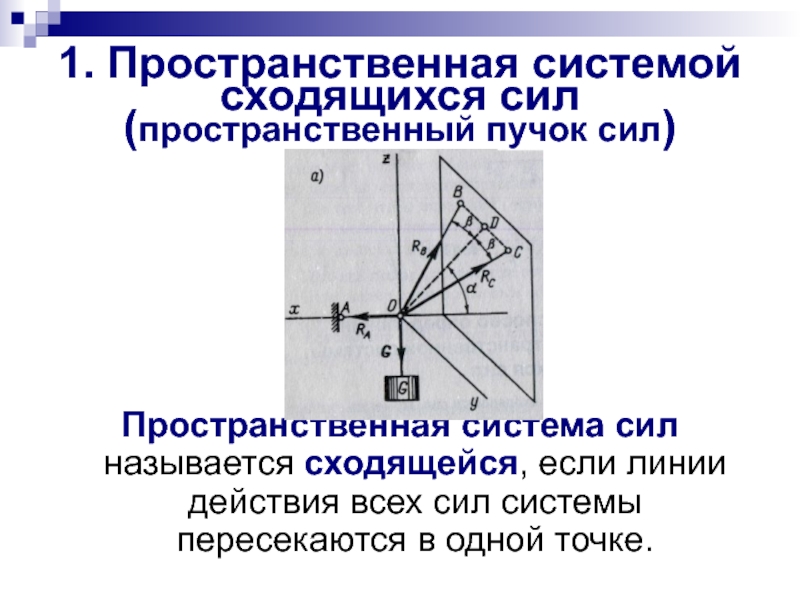
Слайд 61. Пространственная системой сходящихся сил (пространственный пучок сил)
Пространственная система сил называется
Слайд 7Теорема о равнодействующей пространственной ССС. Пространственная система сходящихся сил эквивалентна равнодействующей,
Слайд 8Способы определения равнодействующей силы пространственной системы сходящихся сил:
Силовой многоугольник пространственной
Применяется только аналитический способ
( метод проекций).
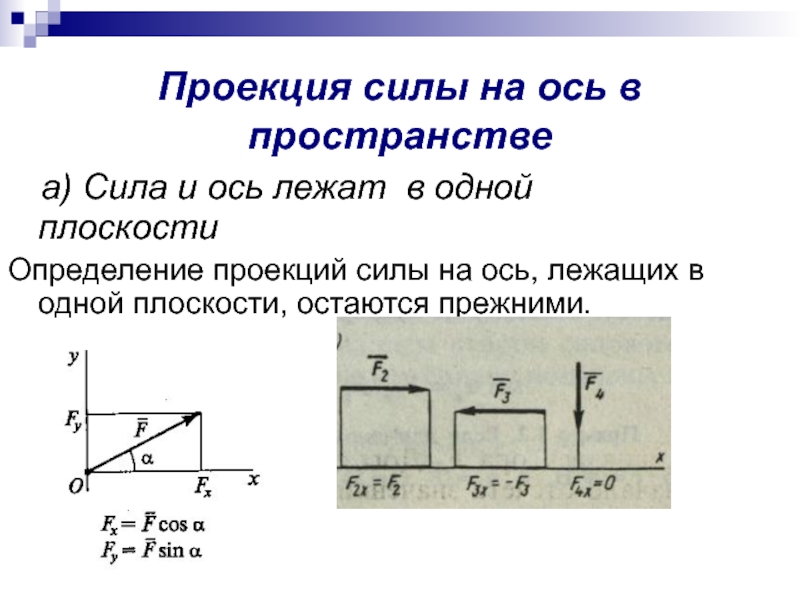
Слайд 9Проекция силы на ось в пространстве
а) Сила и ось
Определение проекций силы на ось, лежащих в одной плоскости, остаются прежними.
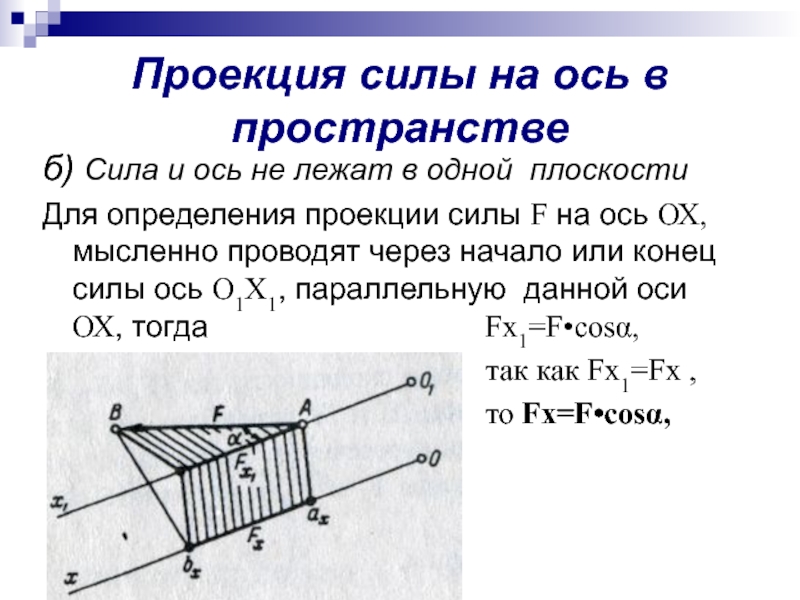
Слайд 10Проекция силы на ось в пространстве
б) Сила и ось не лежат
Для определения проекции силы F на ось ОХ, мысленно проводят через начало или конец силы ось О1Х1, параллельную данной оси ОХ, тогда Fx1=F•cosα,
так как Fx1=Fx ,
то Fx=F•cosα,
Слайд 11Разложение силы по трём осям координат
Равнодействующая трёх взаимно перпендикулярных
F=Fx+Fy+Fz
Слайд 12Модуль и направление равнодействующей силы :
- модуль FƩ
FƩ=√Fx2+Fy2+Fz2 =√(∑Xi)2+(∑Yi)2+(∑Zi)2
- направление FƩ
Cos(FƩ,X)=Fx/FƩ=∑Xi/FƩ
Cos(FƩ,Y)=Fy/FƩ= ∑Yi/FƩ
Cos(FƩ,Z)=Fz/FƩ= ∑Zi/FƩ
Слайд 13Аналитическое условие равновесия пространственной ССС
Для равновесия пространственной ССС
1)∑Fix = ∑Х = 0
FƩ = 0 2)∑Fiy = ∑У = 0
3) ∑Fiz = ∑Z = 0
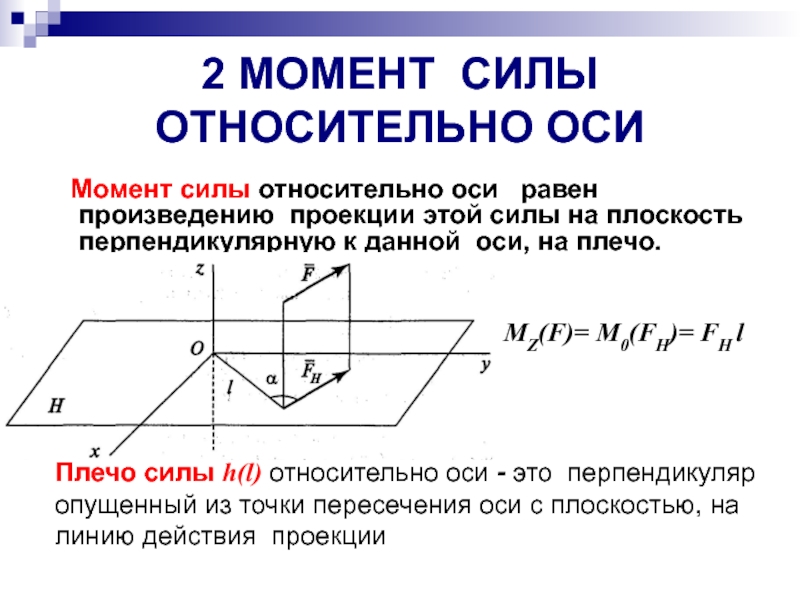
Слайд 142 МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ОСИ
Момент силы относительно оси
МZ(F)= М0(FH)= FH l
Плечо силы h(l) относительно оси - это перпендикуляр опущенный из точки пересечения оси с плоскостью, на линию действия проекции
Слайд 15Правило знаков
Момент силы относительно оси будем считать положительным
Слайд 16Момент силы относительно оси равен нулю в 2 случаях:
1.
2. Если вектор силы параллелен оси
F2//Z , т.к. FH = 0
Слайд 17Пример: В червячной передаче червяк передает червячному колесу, укрепленному на валу,
Разложим силу F на три взаимно перпендикулярные составляющие :
F1 (окружная сила), вызывает вращательное движение, которое измеряется моментом
Мz(F1)= F1 r
F2 (осевая сила) стремится сдвинуть колесо вдоль оси
Fз (радиальная сила) стремится изогнуть ось колеса
Слайд 18
3. Пространственная система произвольно расположенных сил -
это система сил,
Слайд 19 Приведение произвольной пространственной системы сил к заданному центру (Аналогично плоской
Слайд 20
Приведение произвольной пространственной системы сил к заданному центру
Пространственная система произвольно расположенных сил в общем случае эквивалентна одной силе, приложенной в центре приведения и одной паре сил
Произвольная пространственная система сил приводится к главному вектору и главному моменту.
Слайд 21Модуль и направление главного вектора :
- модуль FГЛ
FГЛ=√Fx2+Fy2+Fz2 =√(∑Xi)2+(∑Yi)2+(∑Zi)2
- направление FГЛ
Cos(Fгл; x)= ∑Xi/ Fгл
Cos(Fгл; y)= ∑Yi/ Fгл
Cos(Fгл; z)= ∑Zi/ Fгл
Слайд 22Модуль главного момента :
Алгебраическая сумма моментов всех сил системы относительно каждой
МГЛ = √ (∑МX(Fi))2+(∑МY(Fi))2+ (∑МZ(Fi))2
Слайд 23
Аналитические условия равновесия пространственной системы
произвольно расположенных сил
Алгебраическая сумма
1) ∑X=∑ Fi x =0 4) ∑Mx(Fi) =0 Fгл =0 2) ∑Y=∑ Fi y =0 Мгл =0 5)∑My(Fi) =0
3)∑Z=∑ Fi z =0 6)∑Mz(Fi) =0