- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Принцип Ле-Шателье-Брауна. Термодинамика необратимых процессов. Циклы энергетических установок. (Лекция 6) презентация
Содержание
- 1. Принцип Ле-Шателье-Брауна. Термодинамика необратимых процессов. Циклы энергетических установок. (Лекция 6)
- 2. Возрастание энтропии изолированной системы происходит до тех
- 3. Реакцию системы на внешние воздействия можно качественно
- 4. Пример: Один моль идеального газа находится в
- 5. Отсюда имеем, имеем Так как CP >
- 7. Для точки среды
- 8. Ключевое значение в термодинамике необратимых
- 9. Термодинамика необратимых процессов Если в качестве термодинамических
- 10. В случае небольших отклонений от равновесного состояния
- 11. Коэффициенты Lik называются кинетическими коэффициентами, и они
- 13. Пример возникновения пространственной структуры:
- 15. ДВС – поршневые газовые двигатели, в которых
- 16. 1 -2 Линия всасывания топливно-воздушной
- 17. Для термодинамического анализа рабочий процесс двигателя, как
- 20. Например, для цикла со сгоранием при V
- 21. Цикл компрессорных дизелей, использующих тяжелые топлива с
- 22. Впрыск происходит достаточно долговременно, так что с
- 23. Для изобары b-c имеем:
- 24. КПД цикла Дизеля: где δ =
Слайд 1ТЕХНИЧЕСКАЯ ТЕРМОДИНАМИКА
ПРИНЦИП ЛЕ-ШАТЕЛЬЕ - БРАУНА,
ТЕРМОДИНАМИКА НЕОБРАТИМЫХ ПРОЦЕССОВ,
ЦИКЛЫ ЭНЕРГЕТИЧЕСКИХ УСТАНОВОК
Слайд 2Возрастание энтропии изолированной системы происходит до тех пор, пока в ней
Принцип Ле-Шателье - Брауна
При устойчивом термодинамическом равновесии энтропия адиабатически изолированной системы имеет экстремум: S = S∞, где S∞ - энтропия системы в состоянии термодинамического равновесия. Следовательно, в состоянии устойчивого равновесия первая вариация энтропии изолированной термодинамической системы δS = 0, а вторая ее вариация - δS2 < 0. Условие равенства нулю первой вариации энтропии дает необходимое условие равновесия изолированной системы, а неравенство
δS2 < 0 - достаточное условие устойчивости равновесного состояния
Слайд 3Реакцию системы на внешние воздействия можно качественно определить на основе принципа
Внешние воздействия, выводящие термодинамическую систему из состояния устойчивого равновесия, вызывают в ней протекание процессов, которые уменьшают влияние этих внешних возмущений.
Этот принцип позволяет предсказать направление протекания процессов в термодинамической системе, которая выводится из состояния устойчивого равновесия внешними воздействиями. Например, имеется смесь льда и воды, находящаяся в состоянии устойчивого равновесия. Если этой смеси сообщить некоторое количество теплоты, то лед начнет таять, что будет препятствовать повышению температуры смеси. То есть, протекающий в системе процесс таяния льда будет ослаблять изменения, вызываемые подводом теплоты
Принцип Ле-Шателье - Брауна
Слайд 4Пример: Один моль идеального газа находится в эластичной оболочке, с внешней
Принцип Ле-Шателье - Брауна
Для одного моля идеального газа в случае изобарического процесса:
Для изохорического процесса:
Слайд 5Отсюда имеем, имеем
Так как CP > CV, то ΔT < ΔT0.
Принцип Ле-Шателье - Брауна
Слайд 6
Для описания необратимых процессов можно воспользоваться гипотезой локального равновесия: внутри малого
приходящуюся на единицу массы среды, и удельный объем
где - локальная плотность среды
Термодинамика необратимых процессов
Слайд 7
Для точки среды с координатами {x,y,z} в момент времени t можно
Совместное применение данных уравнений позволяет построить феноменологическую термодинамику необратимых процессов, опирающуюся на использование полученных из опыта соотношений между параметрами, описывающими термодинамические процессы.
Тогда внутренняя энергия всей системы определяется с помощью выражения
а ее энтропия S соответственно может быть найдена по формуле
Термодинамика необратимых процессов
Слайд 8
Ключевое значение в термодинамике необратимых процессов имеет величина, численно равная скорости
Эта величина представляет собой производство энтропии для единичного объема адиабатически изолированной системы. Она описывает количество энтропии, которая возникает в единичном объеме термодинамической системы за единицу времени при протекании в ней необратимых термодинамических процессов
Термодинамика необратимых процессов
Слайд 9Термодинамика необратимых процессов
Если в качестве термодинамических параметров системы выступают N величин
термодинамические силы
плотности термодинамических потоков
Следовательно
Слайд 10В случае небольших отклонений от равновесного состояния между термодинамическими потоками ji
Термодинамика необратимых процессов
Это соответствует наиболее простому случаю термодинамики линейных необратимых процессов. Таким образом, для линейных необратимых процессов производство энтропии определяется выражением
или
Слайд 11Коэффициенты Lik называются кинетическими коэффициентами, и они характеризуют интенсивность явлений переноса.
указывающее на симметрию матрицы кинетических коэффициентов.
Термодинамика необратимых процессов
Одним из принципов термодинамики линейных необратимых процессов является предложенный в 1947 году бельгийским физико-химиком Ильей Романовичем Пригожиным принцип минимума производства энтропии: Стационарные необратимые процессы протекают таким образом, чтобы производство энтропии было минимальным.
Слайд 12
Принцип минимума производства энтропии позволяет установить критерий отбора реализующихся в природе
Необходимость выполнения указанного принципа приводит к тому, что при протекании в среде необратимых стационарных процессов возникают динамические структуры, названные Пригожиным диссипативными структурами, что уменьшает производство энтропии. Примером таких структур могут служить ячейки Бенара - регулярные динамические структуры, возникающие в тонком слое нагреваемой снизу жидкости, и колебательные химические реакции Б.П. Белоусова, при которых происходят периодические изменения концентрации реагирующих веществ.
Термодинамика необратимых процессов
Слайд 13
Пример возникновения пространственной структуры: «Ячейки Бенара».
Термодинамика необратимых процессов
Слайд 14
Термодинамика необратимых процессов
Примером временной структуры является реакция Белоусова
Реакция Белоусова – Жаботинского наблюдается в реакционной смеси, состоящей из бромата калия (KBr), броммалоновой кислоты, сульфата церия (Се).
Смесь нужно растворить либо в лимонной, либо в серной кислоте. Окраска раствора через 4 мин изменяется с синего на красный (и наоборот).
Это происходит в связи с восстановлением ионов церия:
Се+4 ↔ Се+3
Чередование окраски раствора является самоорганизованным, развивающимся во времени.
Слайд 15ДВС – поршневые газовые двигатели, в которых продукты сгорания топлива являются
Основная часть ДВС – цилиндр с поршнем.
На крышке цилиндра устанавливаются 2 клапана для впрыска рабочего тела и для выпуска отработанных газов. В таком двигателе горючая смесь сгорает с повышением температуры, а иногда и давления. Продукты сгорания, воздействуя на поршень, перемещают его из одного крайнего состояния в другое. При этом совершается работа расширения. Поршневой принцип осуществляется в двигателях мощностью до 30 МВт
Циклы двигателей внутреннего сгорания
В ДВС реализуются циклы: с подводом теплоты при постоянном объеме (цикл Отто, 1876), с подводом теплоты при постоянном давлении (цикл Дизеля, 1892) и со смешанным подводом теплоты (цикл Тринклера, 1901).
Слайд 16
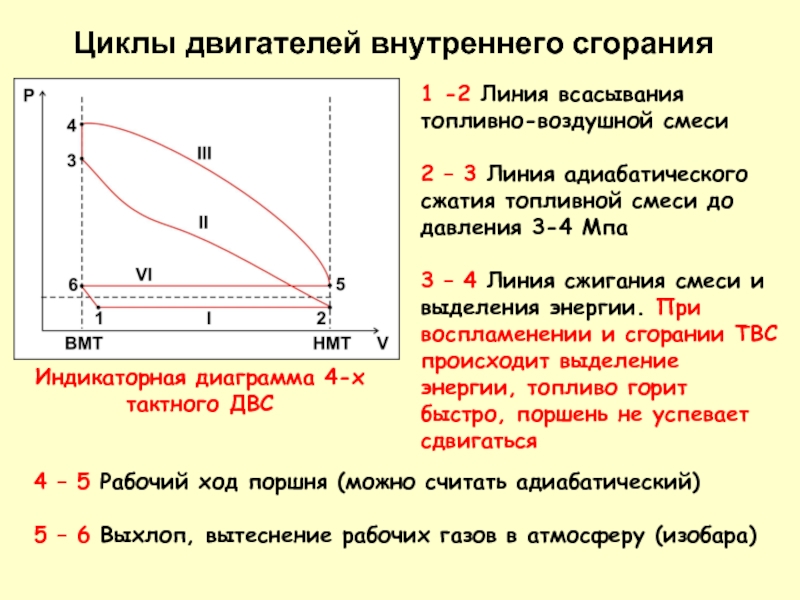
1 -2 Линия всасывания топливно-воздушной смеси
2 – 3 Линия адиабатического сжатия
3 – 4 Линия сжигания смеси и выделения энергии. При воспламенении и сгорании ТВС происходит выделение энергии, топливо горит быстро, поршень не успевает сдвигаться
Индикаторная диаграмма 4-х тактного ДВС
4 – 5 Рабочий ход поршня (можно считать адиабатический)
5 – 6 Выхлоп, вытеснение рабочих газов в атмосферу (изобара)
Циклы двигателей внутреннего сгорания
Слайд 17Для термодинамического анализа рабочий процесс двигателя, как правило, заменяют идеальным термодинамическим
Процесс горения смеси заменяют процессом подвода тепла извне
Процесс выхлопа заменяют отводом тепла во внешнюю среду
Потерями на теплообмен и трение пренебрегают
Считается, что рабочее тело не обновляется, т.е. система замкнутая
Циклы двигателей внутреннего сгорания
Слайд 18
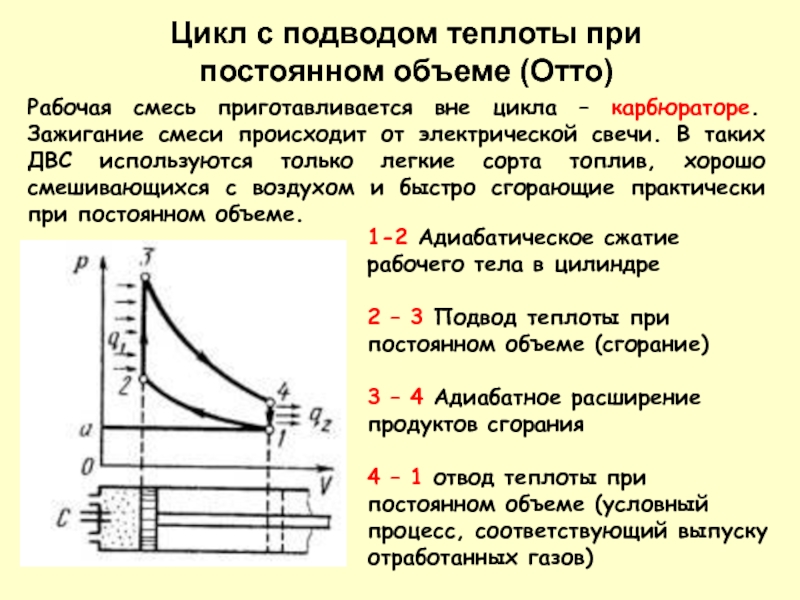
Рабочая смесь приготавливается вне цикла – карбюраторе. Зажигание смеси происходит от
1-2 Адиабатическое сжатие рабочего тела в цилиндре
2 – 3 Подвод теплоты при постоянном объеме (сгорание)
3 – 4 Адиабатное расширение продуктов сгорания
4 – 1 отвод теплоты при постоянном объеме (условный процесс, соответствующий выпуску отработанных газов)
Цикл с подводом теплоты при постоянном объеме (Отто)
Слайд 19
Чтобы не делать цилиндр очень длинным, а ход поршня большим, расширение
Цикл с подводом теплоты при постоянном объеме (Отто)
Степень сжатия двигателя ε - отношение полного объема цилиндра к объему камеры сгорания.
Степень сжатия двигателя – основной параметр, определяющий термический КПД цикла.
Термический КПД цикла ДВС увеличивается с ростом степени сжатия.
Слайд 20Например, для цикла со сгоранием при V = const, при постоянной
При одинаковых показателях адиабаты k процессов сжатия и расширения можно записать:
В карбюраторном двигателе максимальная степень сжатия ограничивается самовоспламенением ТВС и не превышает 9-10. В дизелях, в которых поршень сжимает воздух, ε ≈ 18, что позволяет существенно повысить КПД цикла.
Тогда:
Цикл с подводом теплоты при постоянном объеме (Отто)
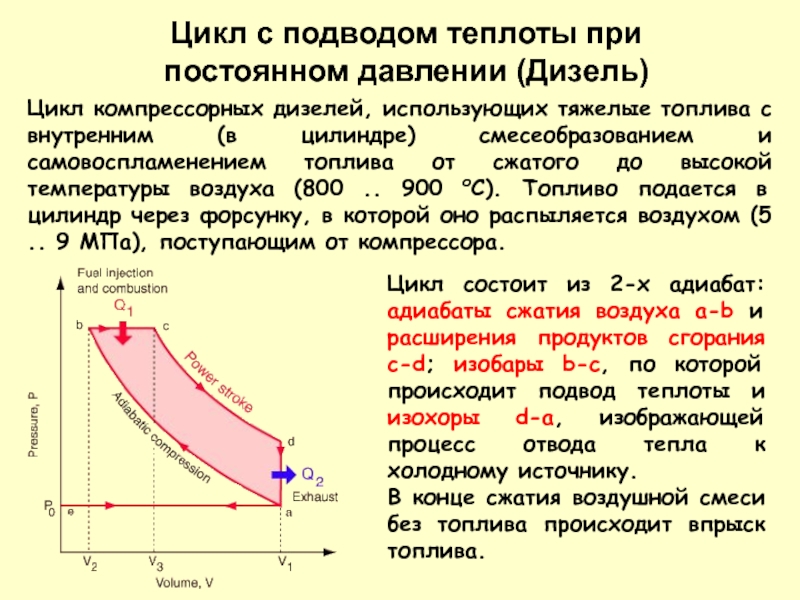
Слайд 21Цикл компрессорных дизелей, использующих тяжелые топлива с внутренним (в цилиндре) смесеобразованием
Цикл состоит из 2-х адиабат: адиабаты сжатия воздуха a-b и расширения продуктов сгорания c-d; изобары b-c, по которой происходит подвод теплоты и изохоры d-a, изображающей процесс отвода тепла к холодному источнику.
В конце сжатия воздушной смеси без топлива происходит впрыск топлива.
Цикл с подводом теплоты при постоянном давлении (Дизель)
Слайд 22Впрыск происходит достаточно долговременно, так что с отводом поршня от ВМТ
Ведем степень предварительного расширения:
Цикл с подводом теплоты при постоянном давлении (Дизель)
Слайд 23Для изобары b-c имеем:
Для адиабаты c-d:
Цикл с подводом теплоты при постоянном
Аналогично для a-b:
Отсюда:
Слайд 24КПД цикла Дизеля:
где δ = V1/V3 – степень адиабатного расширения
С учетом
Цикл с подводом теплоты при постоянном давлении (Дизель)