- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Примеры расчета магнитных полей презентация
Содержание
- 1. Примеры расчета магнитных полей
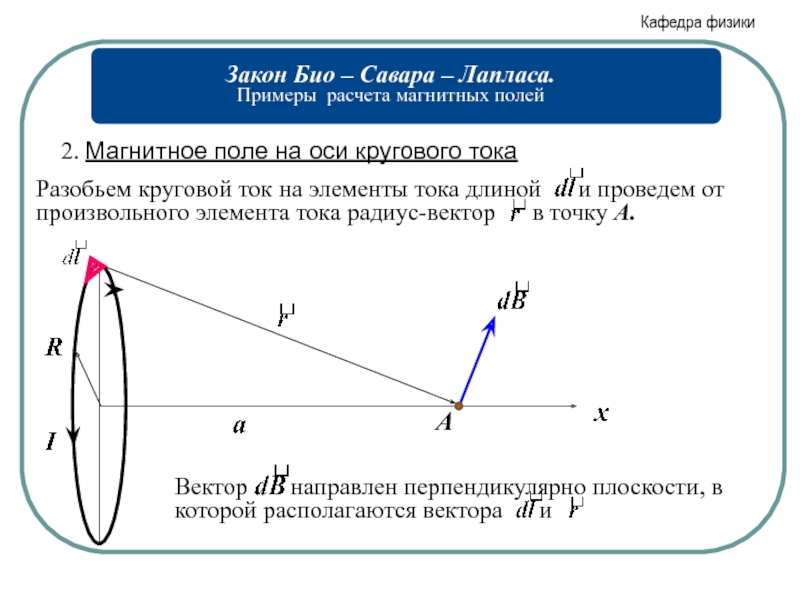
- 2. Магнитное поле на оси кругового тока А
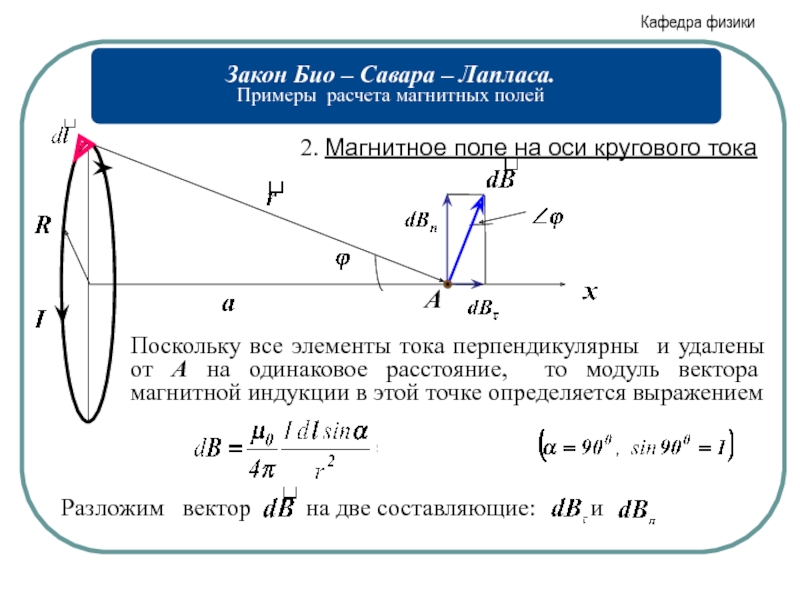
- 3. 2. Магнитное поле на оси кругового тока
- 4. 2. Магнитное поле на оси кругового тока
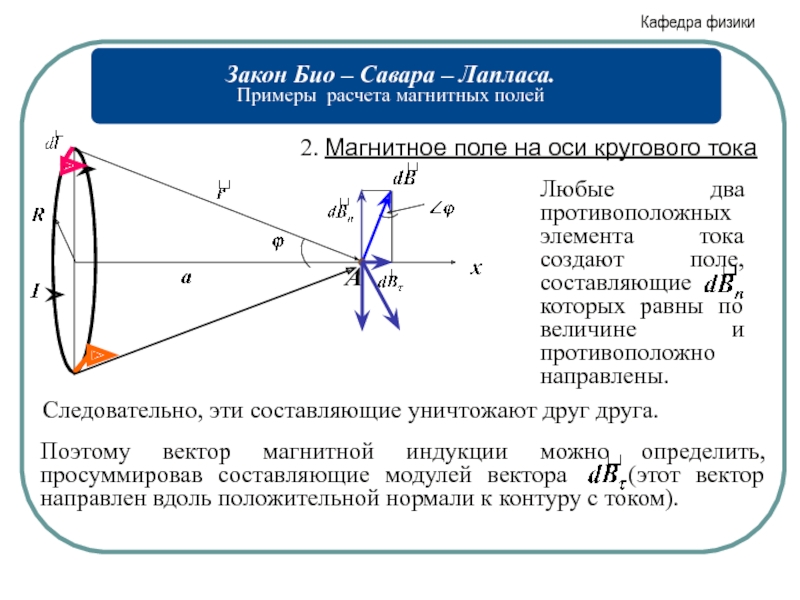
- 5. 2. Магнитное поле на оси кругового тока Следовательно, эти составляющие уничтожают друг друга.
- 6. 2. Магнитное поле на оси кругового тока
- 7. 2. Магнитное поле на оси кругового тока
- 8. 2. Магнитное поле на оси кругового тока
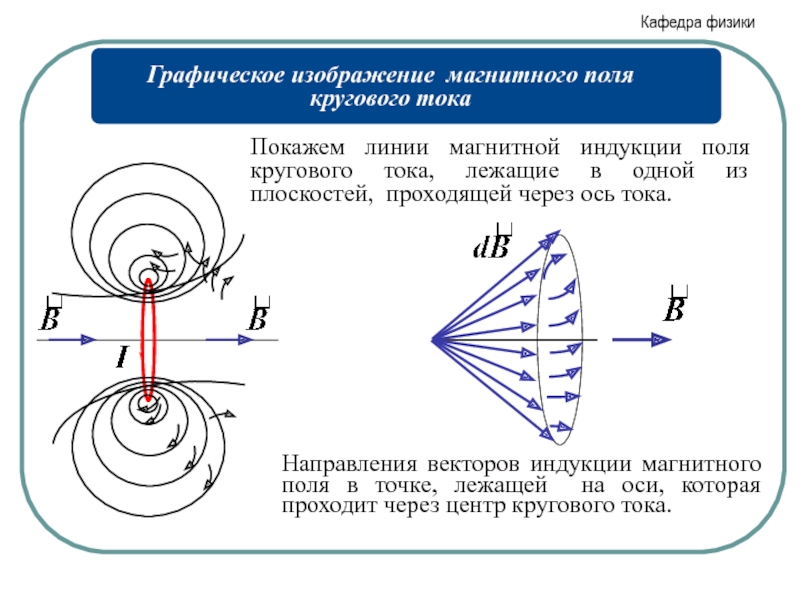
- 9. Покажем линии магнитной индукции поля кругового тока,
- 10. Для замкнутой поверхности:
- 11. теорема Гаусса-Остроградского для магнитного поля.
- 12. Важное следствие из теоремы Гаусса: Уравнение Гаусса
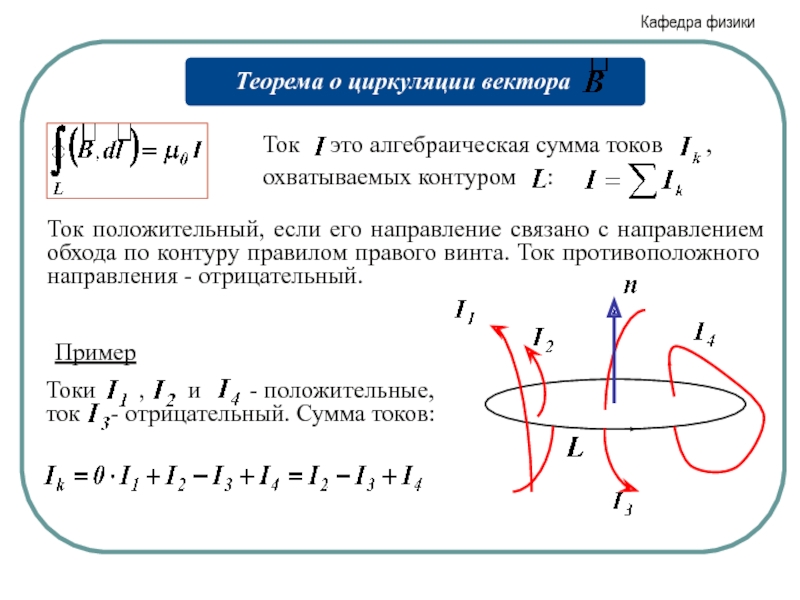
- 14. Ток положительный, если его направление связано с
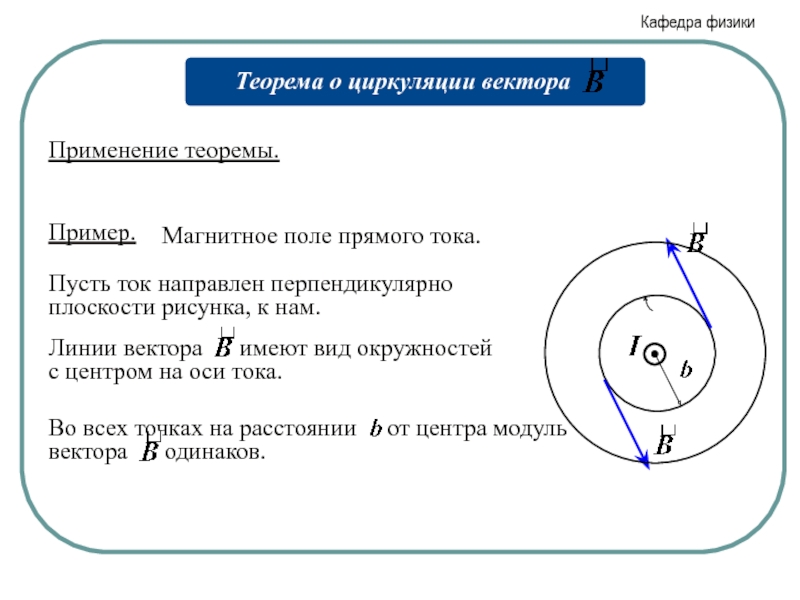
- 16. Пример. Магнитное поле прямого тока.
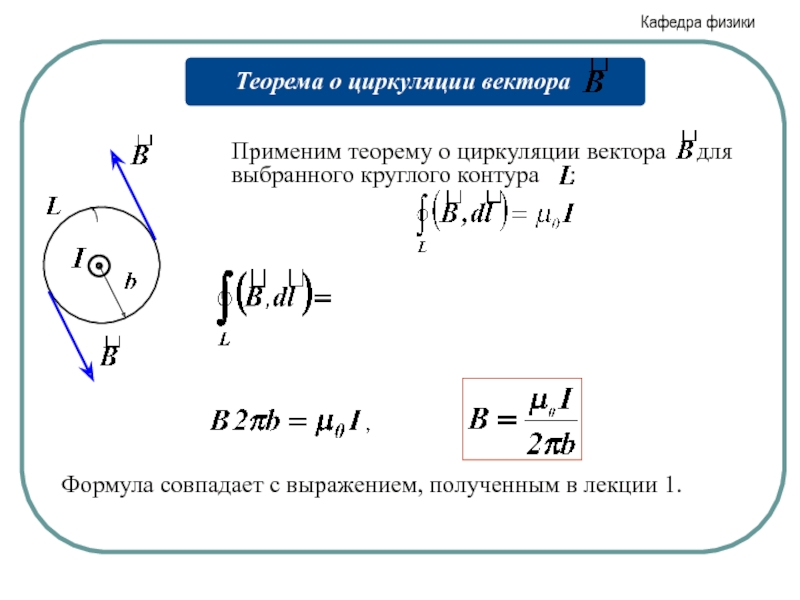
- 17. Формула совпадает с выражением, полученным в лекции 1.
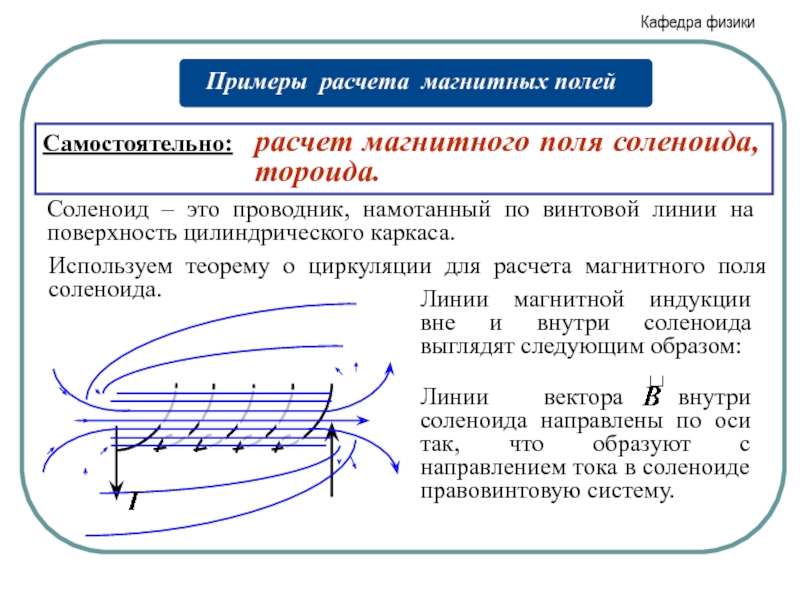
- 18. Используем теорему о циркуляции для расчета магнитного
- 19. Магнитное поле соленоида Если шаг винтовой линии
- 20. Магнитное поле соленоида А С В
- 21. Магнитное поле соленоида В итоге получаем:
- 22. Магнитное поле соленоида Некорректность при
Слайд 42. Магнитное поле на оси кругового тока
Поскольку все элементы тока
Слайд 52. Магнитное поле на оси кругового тока
Следовательно, эти составляющие уничтожают
Слайд 62. Магнитное поле на оси кругового тока
Преобразуем полученное выражение, учитывая,
После подстановки:
Слайд 9Покажем линии магнитной индукции поля кругового тока, лежащие в одной из
Направления векторов индукции магнитного поля в точке, лежащей на оси, которая проходит через центр кругового тока.
Слайд 11
теорема Гаусса-Остроградского для магнитного поля.
Поток вектора напряженности магнитного поля через
Единица магнитного потока в СИ - вебер (Вб).
Слайд 12Важное следствие из теоремы Гаусса:
Уравнение Гаусса в дифференциальной форме:
Из векторного анализа:
Физическая причина соленоидальности магнитного поля - отсутствие свободных магнитных зарядов, аналогичных электрическим зарядам.
Слайд 14Ток положительный, если его направление связано с направлением обхода по контуру
Пример
Слайд 16Пример.
Магнитное поле прямого тока.
Пусть ток направлен перпендикулярно плоскости рисунка,
Применение теоремы.
Слайд 18Используем теорему о циркуляции для расчета магнитного поля соленоида.
Соленоид –
Линии магнитной индукции вне и внутри соленоида выглядят следующим образом:
Самостоятельно: расчет магнитного поля соленоида, тороида.
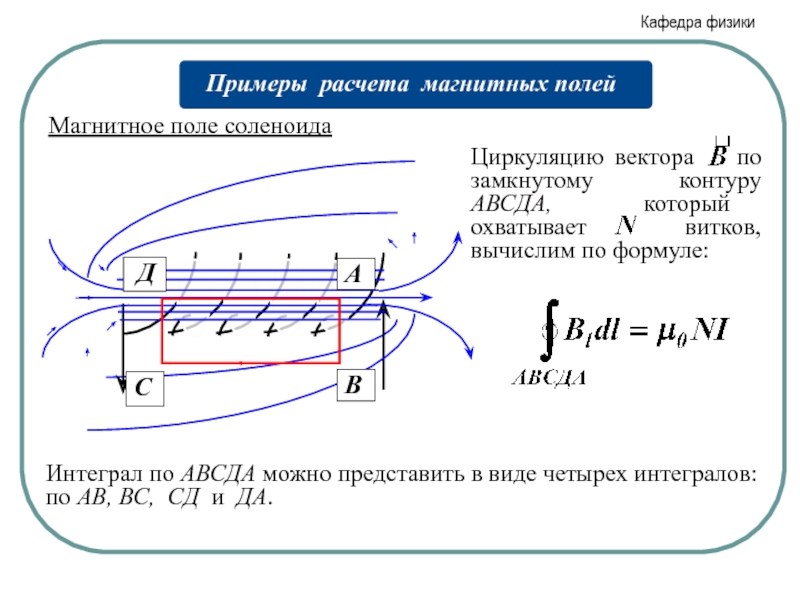
Слайд 19Магнитное поле соленоида
Если шаг винтовой линии мал, то каждый виток соленоида
Из опыта: чем длиннее соленоид, тем меньше поле вне его. Поле бесконечно длинного соленоида сосредоточено внутри его, поле снаружи отсутствует.
Для расчета поля внутри соленоида выберем прямоугольный контур и вычислим циркуляцию магнитного поля по этому контуру.
Слайд 20Магнитное поле соленоида
А
С
В
Д
Интеграл по АВСДА можно представить в виде четырех
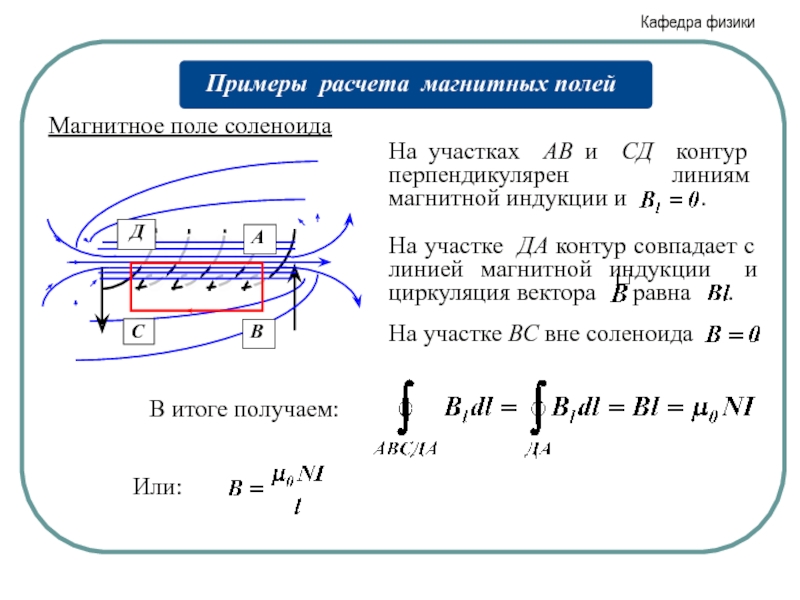
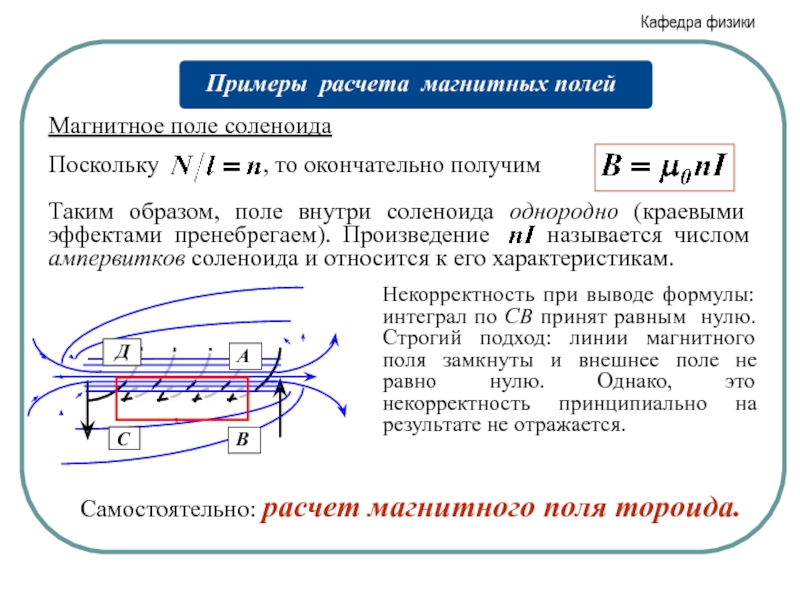
Слайд 22Магнитное поле соленоида
Некорректность при выводе формулы: интеграл по СВ принят равным
Самостоятельно: расчет магнитного поля тороида.