- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Появление хаоса в детерминированных системах презентация
Содержание
- 1. Появление хаоса в детерминированных системах
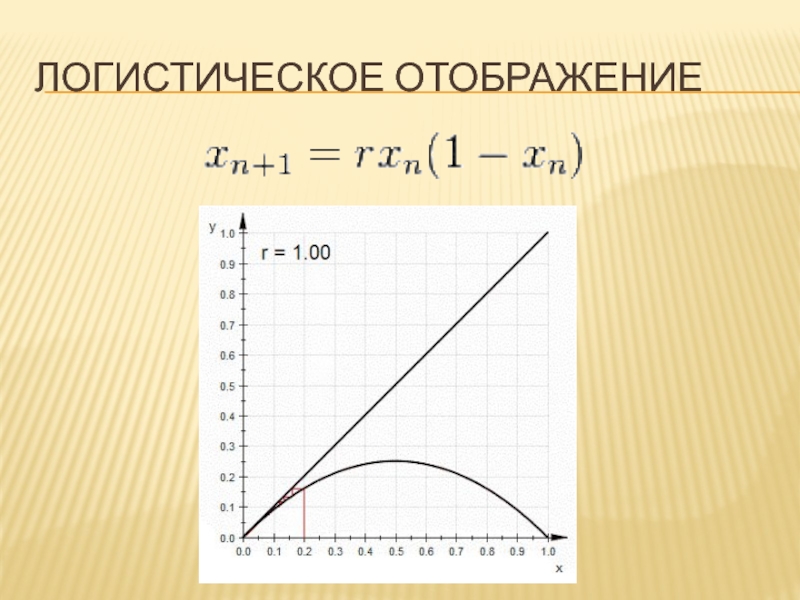
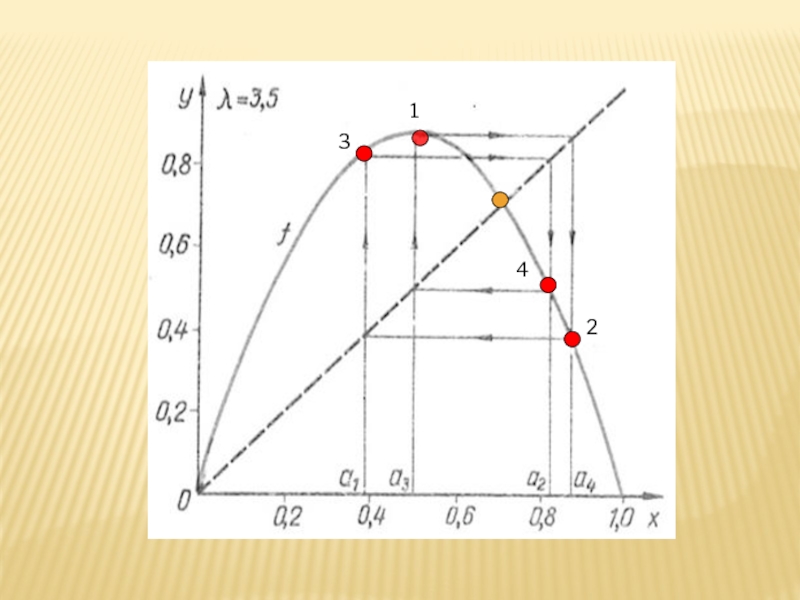
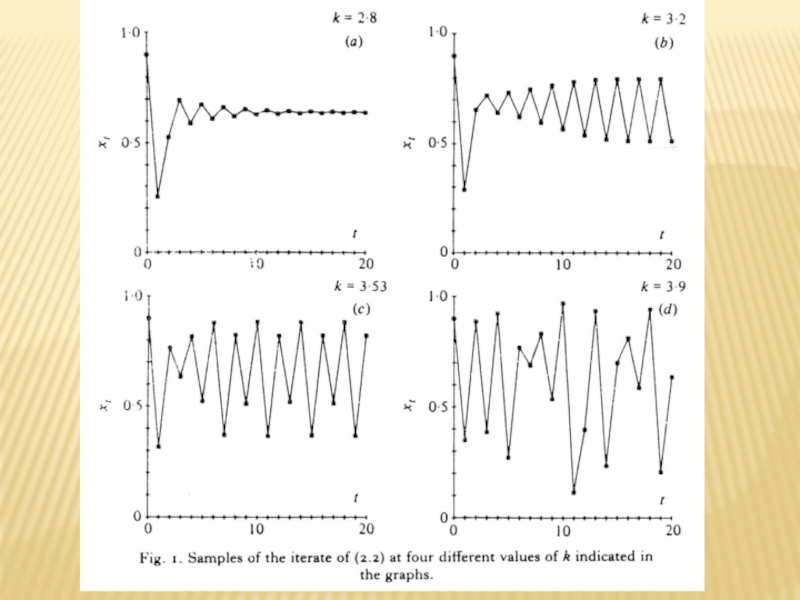
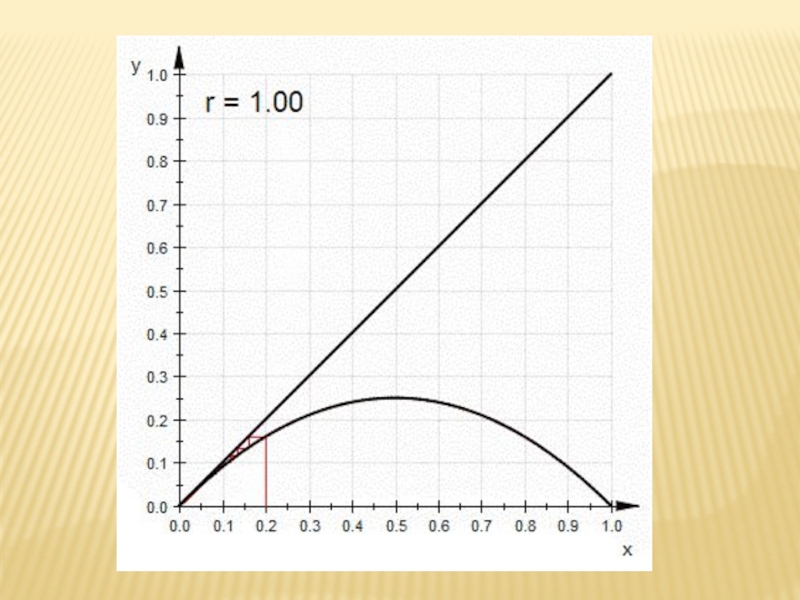
- 2. ЛОГИСТИЧЕСКОЕ ОТОБРАЖЕНИЕ
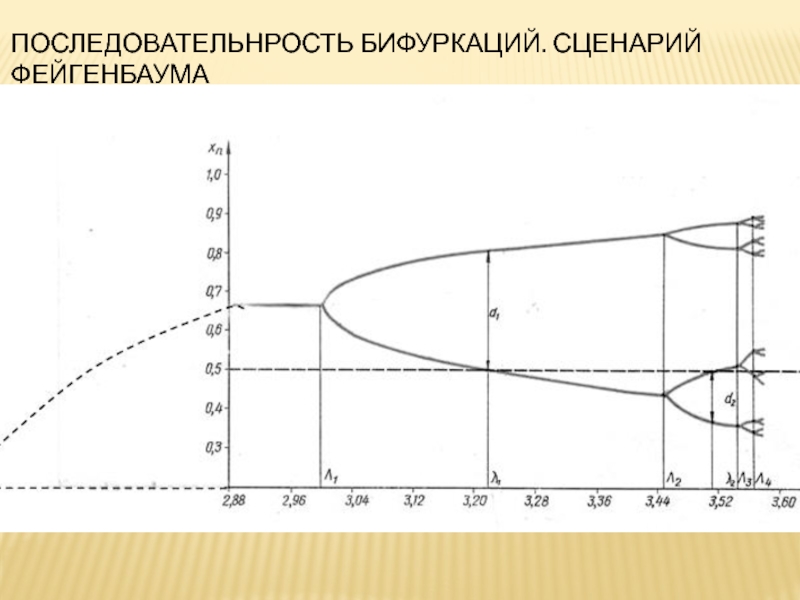
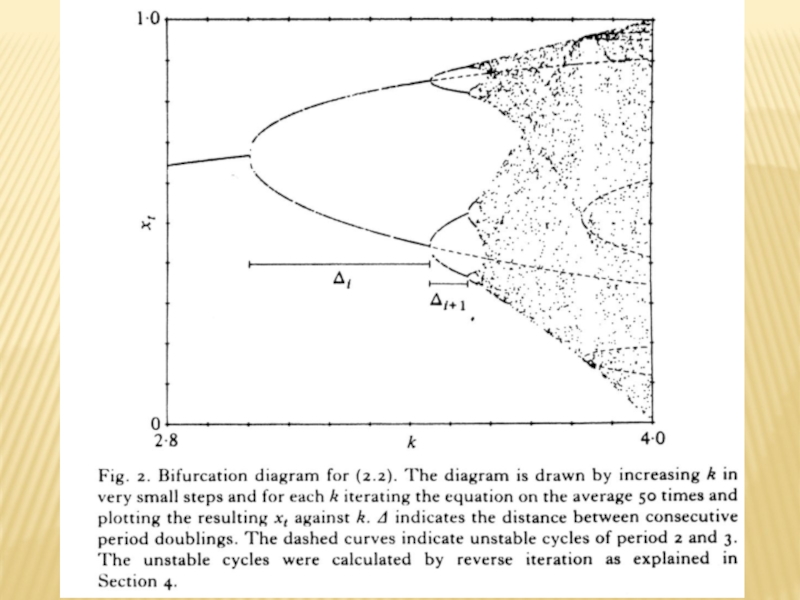
- 9. ПОСЛЕДОВАТЕЛЬНРОСТЬ БИФУРКАЦИЙ. СЦЕНАРИЙ ФЕЙГЕНБАУМА
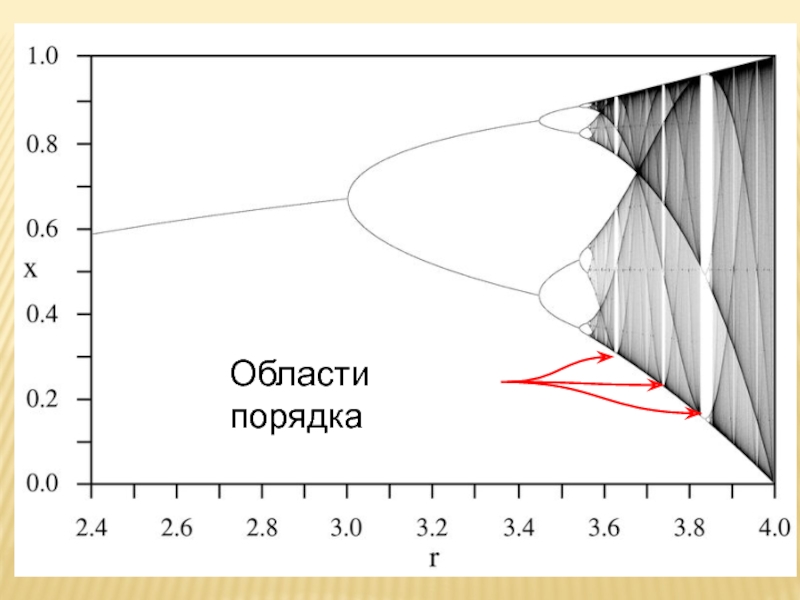
- 10. Области порядка
- 14. ВОЗВРАЩЕНИЕ ПУАНКАРЕ хаос Область порядка порядок
- 15. СЛУЧАЙНЫЕ ПРОЦЕССЫ ШУМЫ
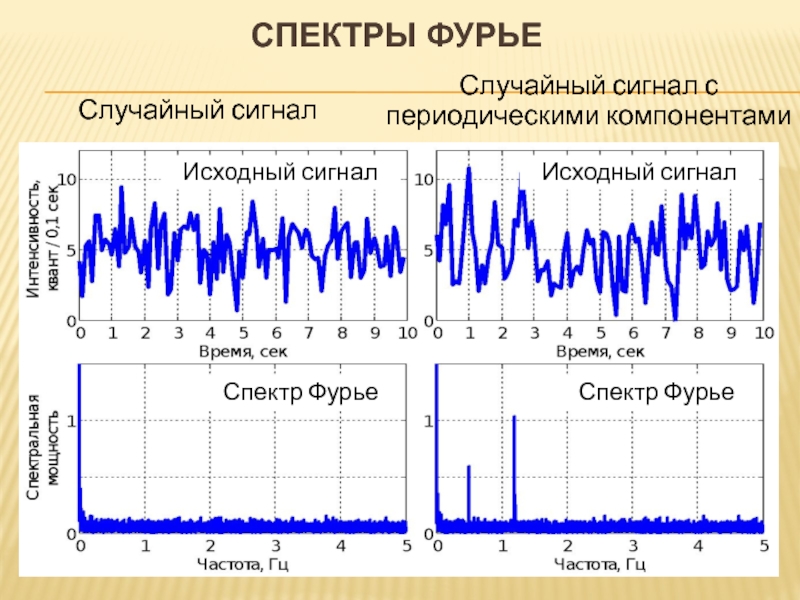
- 16. Случайный сигнал Случайный сигнал с периодическими компонентами СПЕКТРЫ ФУРЬЕ
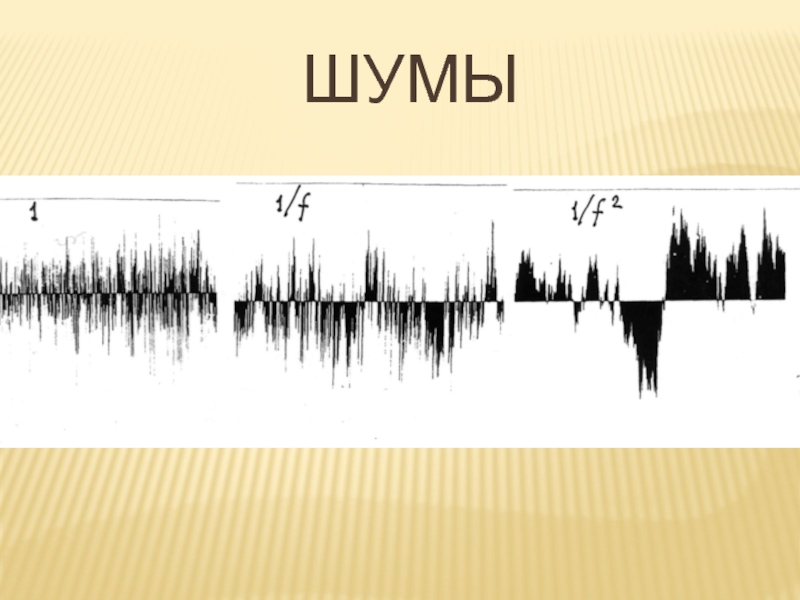
- 17. ШУМЫ
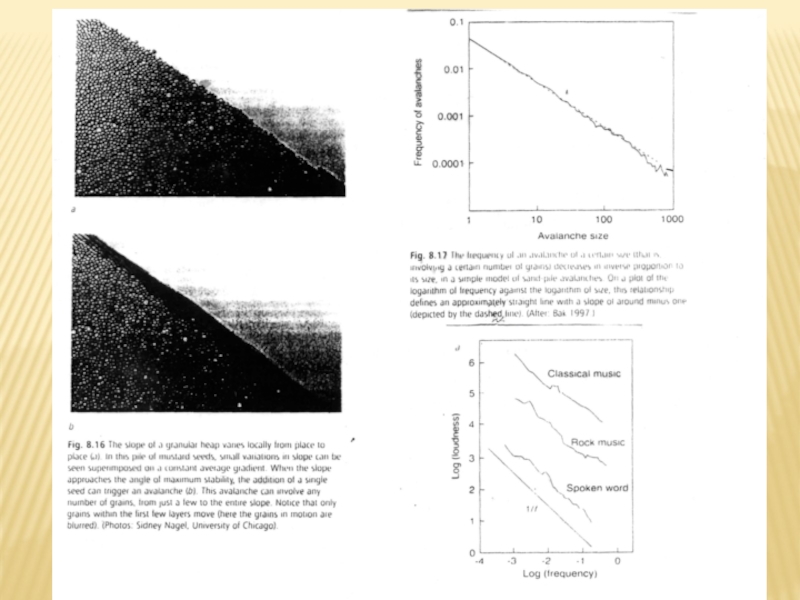
- 19. СТЕПЕННЫЕ РАСПРЕДЕЛЕНИЯ В ПРИРОДЕ
- 20. МЕХАНИЗМЫ ПОЯВЛЕНИЯ СТЕПЕННЫХ ЗАКОНОВ 1. Связь
- 21. МЕХАНИЗМЫ ПОЯВЛЕНИЯ СТЕПЕННЫХ ЗАКОНОВ 4. Пороговые явления
- 22. МЕХАНИЗМЫ ПОЯВЛЕНИЯ СТЕПЕННЫХ ЗАКОНОВ 5. Самоорганизующаяся критичность. Рост деревьев VS. пожары. Самоподдержание вблизи критической точки.
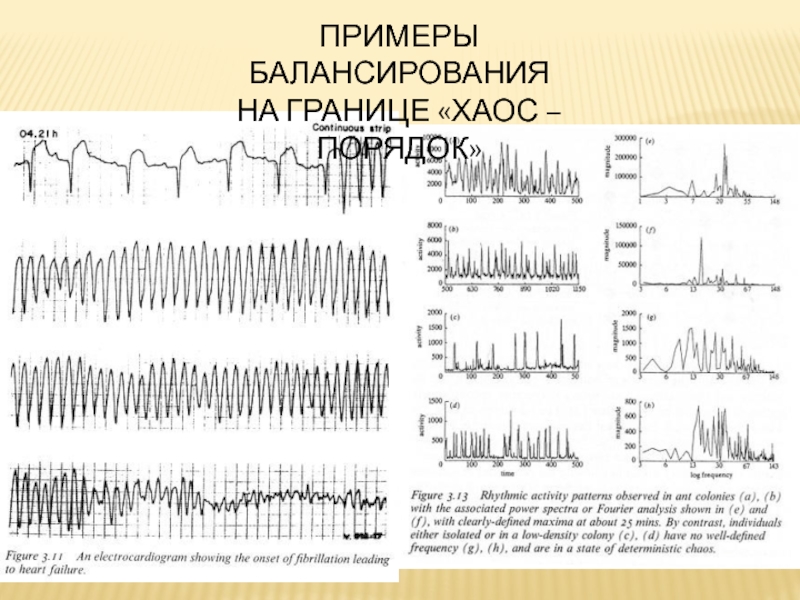
- 23. ПРИМЕРЫ БАЛАНСИРОВАНИЯ НА ГРАНИЦЕ «ХАОС – ПОРЯДОК»
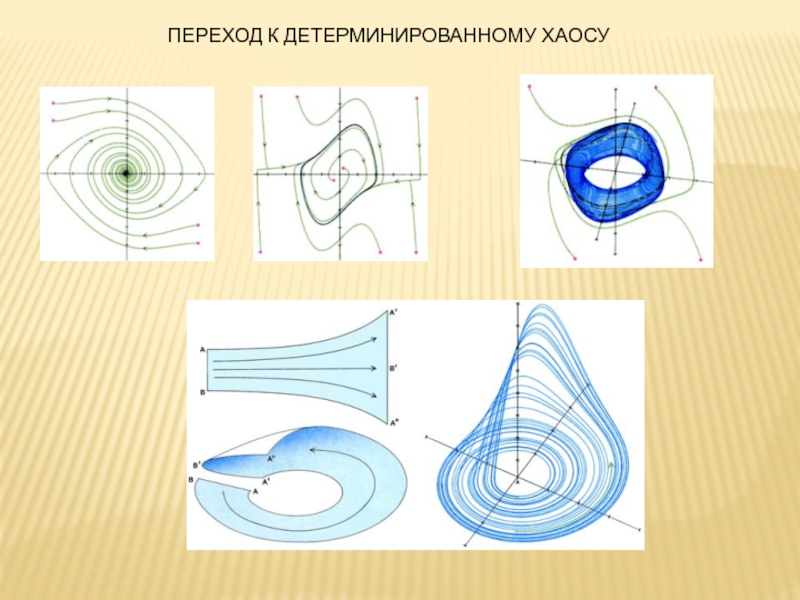
- 24. ПЕРЕХОД К ДЕТЕРМИНИРОВАННОМУ ХАОСУ
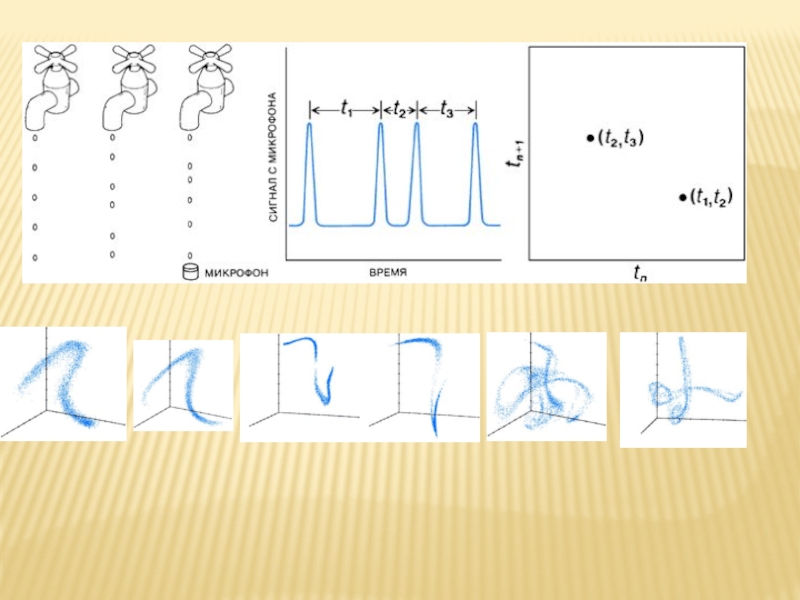
- 25. РАСХОЖДЕНИЕ ТРАЕКТОРИЙ В ПРЕДЕЛАХ СТРАННОГО АТТРАКТОРА dx/dt
- 29. АВТОКОРРЕЛЯЦИИ ПРИ МЕХАНОЭМИССИИ КРОВИ
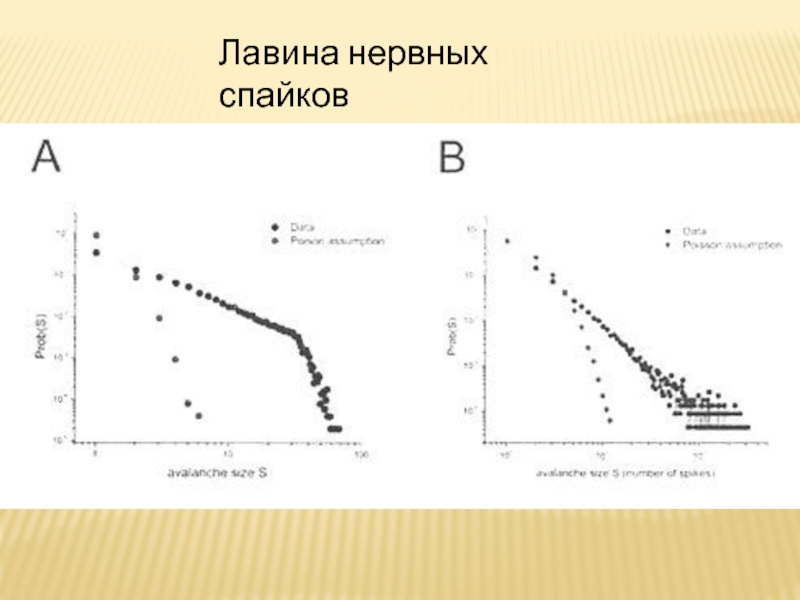
- 30. Лавина нервных спайков
- 31. ФРАКТАЛЬНЫЕ КОЛЕБАНИЯ О2 И СО2 В КУЛЬТУРАХ ДРОЖЖЕЙ (AON et al. 2008)
- 32. Частота встречаемости пятен определенного размера 16 ч
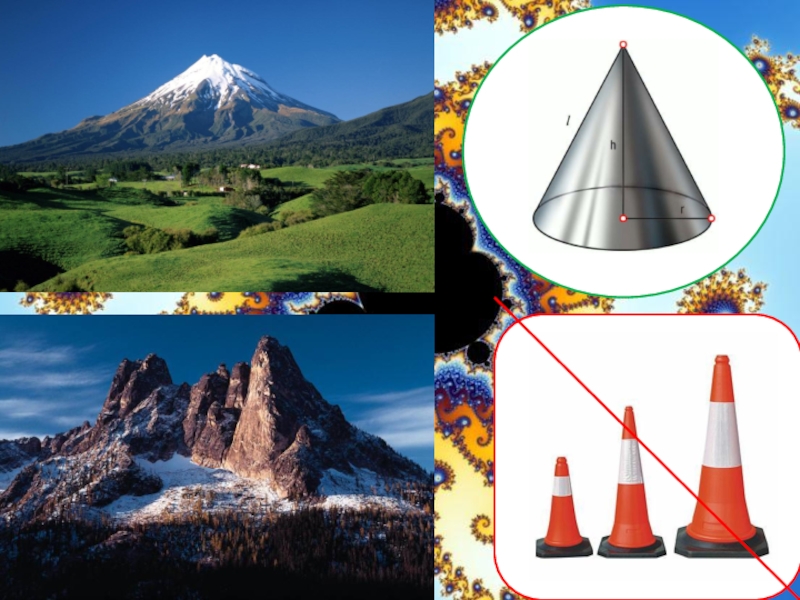
- 33. ФРАКТАЛЫ
- 34. -сложная геометрическая фигура, обладающая свойством самоподобия, т.е.
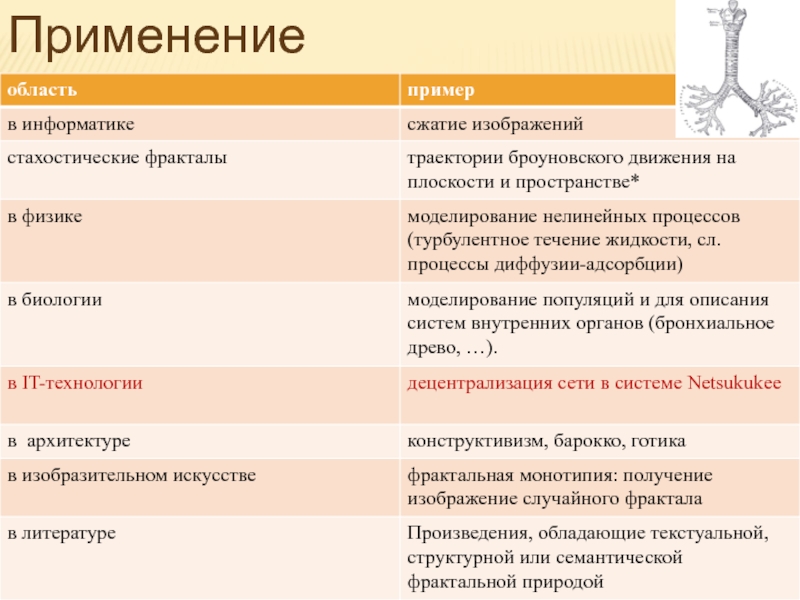
- 35. Применение
- 36. Бенуа Мандельброт (1980) С. Кранц: Р.
- 37. 20.11.1924 – 14.10.2010 С/х Химия Математика
- 40. «Природа демонстрирует совсем другой уровень сложности»
- 41. 1) нетривиальная структура на всех масшатабах, повышение
- 42. 1) задать произвольную ломаную с конечным числом
- 43. Мера Минковского
- 44. -множество точек в евклидовом пространстве, имеющие дробную
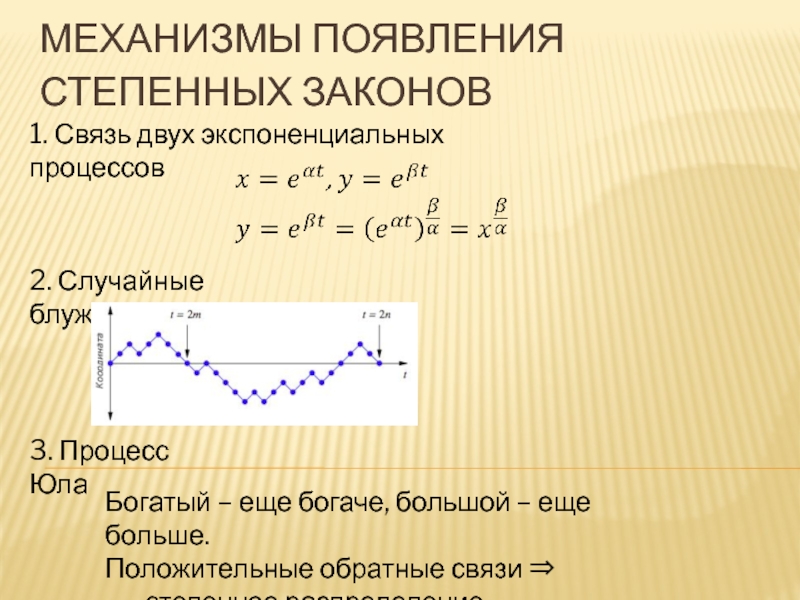
Слайд 20МЕХАНИЗМЫ ПОЯВЛЕНИЯ
СТЕПЕННЫХ ЗАКОНОВ
1. Связь двух экспоненциальных процессов
2. Случайные блуждания
3. Процесс Юла
Богатый
Слайд 21МЕХАНИЗМЫ ПОЯВЛЕНИЯ
СТЕПЕННЫХ ЗАКОНОВ
4. Пороговые явления в перколяции.
Решетка размера N×N.
Вероятность окрашивания клетки
Средний размер кластера –
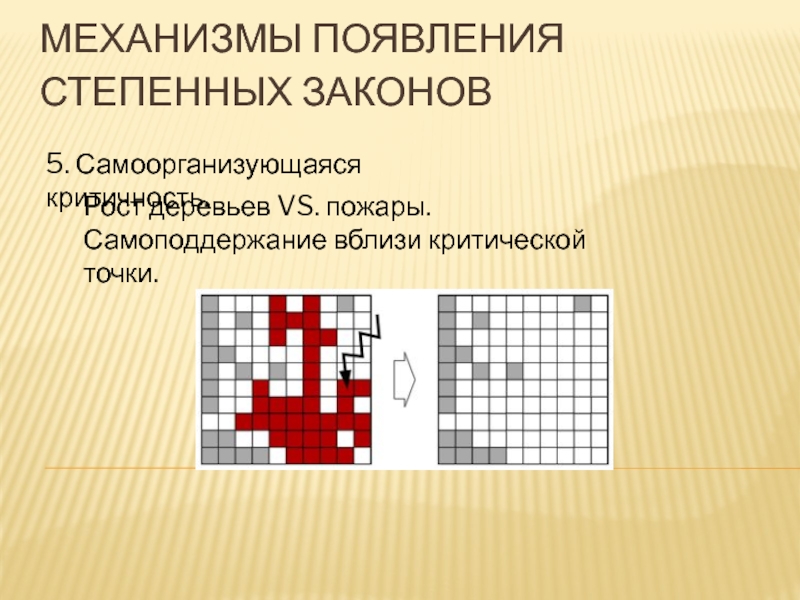
Слайд 22МЕХАНИЗМЫ ПОЯВЛЕНИЯ
СТЕПЕННЫХ ЗАКОНОВ
5. Самоорганизующаяся критичность.
Рост деревьев VS. пожары.
Самоподдержание вблизи критической точки.
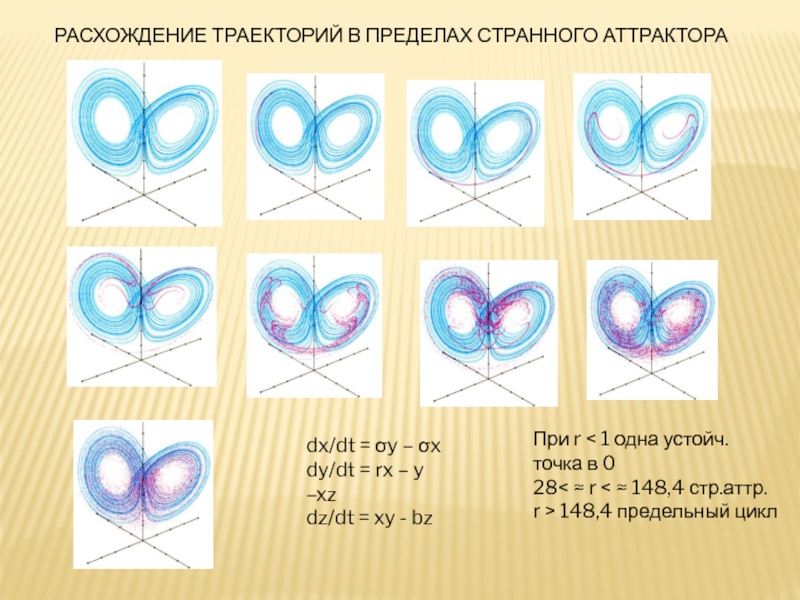
Слайд 25РАСХОЖДЕНИЕ ТРАЕКТОРИЙ В ПРЕДЕЛАХ СТРАННОГО АТТРАКТОРА
dx/dt = σy – σx
dy/dt =
dz/dt = xy - bz
При r < 1 одна устойч.
точка в 0
28< ≈ r < ≈ 148,4 стр.аттр.
r > 148,4 предельный цикл
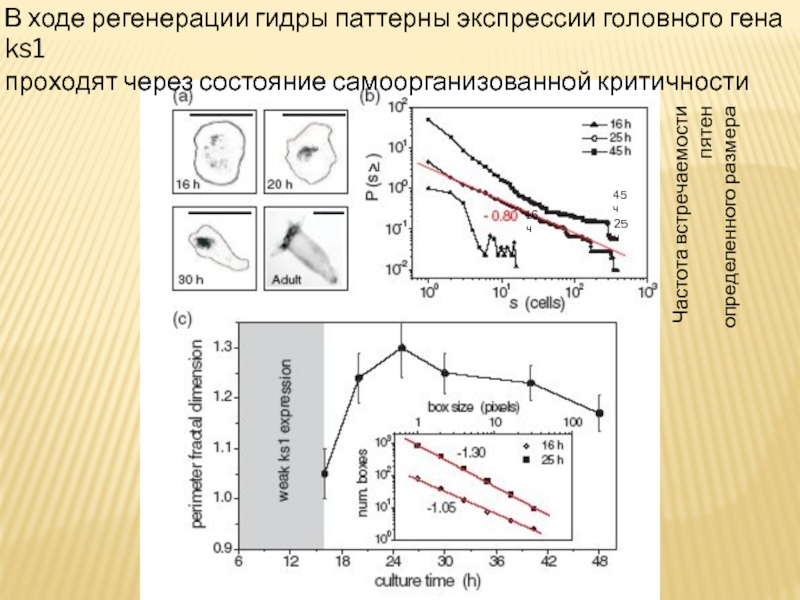
Слайд 32Частота встречаемости пятен
определенного размера
16 ч
25ч
45 ч
В ходе регенерации гидры паттерны экспрессии
проходят через состояние самоорганизованной критичности
Слайд 34-сложная геометрическая фигура, обладающая свойством самоподобия, т.е. составленная из нескольких частей,
Fractus, лат. «дробленный»«сломанный».
Слайд 36
Бенуа Мандельброт (1980)
С. Кранц: Р. Брукс, Дж. Мателски (1978)
Дж. Хаббард (1976)-
Ф. Рисс (1952)
Хаббард
Мателски
Брукс
Пьер Фату (1906)
Людвиг Прандтль (1904)
Лоренц
Пьер Симон Лаплас
Гельмгольц
Кирхгофф
Рэлей
Ляв
Лэмб
Бассет
«Интегрирование встречается и у Архимеда, дифференцирование у Паскаля и Ферма, связь между обеими была известна Барроу. Ньютон изобрел ряды Тейлора-основное орудие анализа».
В.И. Арнольд
Историческая справка
Слайд 37
20.11.1924 – 14.10.2010
С/х
Химия
Математика
Медицина
Физика
Искусство
Мать: Белла Лурие
Отец: Карл Мандельброт
Дядя: Шолем
Бенуа Мандельброт
Слайд 40
«Природа демонстрирует совсем другой уровень сложности»
?
Слайд 411) нетривиальная структура на всех масшатабах, повышение масштаба для фрактальных фигур
2) является самоподобной или приближенно самоподобной;
3) обладает дробной метрической размерностью или метрической размерностью, превосходящей топологическую.
Необходимые условия для фрактальной фигуры:
Слайд 421) задать произвольную ломаную с конечным числом звеньев;
2) заменить в ней
3) в получившейся ломаной вновь заменить каждый отрезок генератором.
Пример получения фрактальных кривых на плоскости
Слайд 44-множество точек в евклидовом пространстве, имеющие дробную метрическую размерность.
Фрактал - это
Под
Живёт блоху кусающая блошка;
На блошке той блошинка-крошка,
В блошинку же вонзает зуб сердито
Блошиночка, и так ad infinitum.
(Джонатан Свифт)